某发动机弹性密封贴合面轴向变形量计算*

周龙超 赵亚飞 赵丹诚

（1.中国航空发动机集团公司四川燃气涡轮研究院；2.深圳大学电子与信息工程学院）

0 引言

为防止某发动机轴承腔内介质泄漏，需在筒体与机匣界面间安装一处弹性密封[1]，该界面间温度最大达到659.5K（386.35℃），远远超过常规氟橡胶的使用温度（250℃[2]），故需安装一种耐高温的弹性密封环[3]结构进行有效密封。弹性密封拟采用高温薄壁金属包裹聚酰亚胺材料制作。考虑密封件本身主体为橡塑材料，应力较小，因此本文忽略安装时应力对两个金属组件的变形影响。

因为弹性密封环的轴向压缩率和回弹率都必须在某一特定范围[4]内，为了评估相邻零件热变形[3]对弹性密封环的影响，需准确、定量计算出弹性密封环的压缩回弹空间[5-6]的轴向变化量，而得到密封环的压缩回弹空间的轴向变化量，必须首先计算筒体和机匣与弹性密封环接触面的轴向变形量[7]。

筒体和机匣为复杂异形结构，采用体积膨胀线性公式[8]计算两个端面的膨胀量的方法已不再适用。本文采用有限元法分别对筒体和机匣进行轴向变形量的分析计算，最后通过二者求差值的方法得到了弹性密封环轴向变形量的精确解，为进一步评估变形量对弹性密封环的影响提供了依据。

1 筒体与机匣变形量计算

筒体与机匣的安装示意图见图1，图中在A 面与B 面之间安装有一处弹性密封环，A 面属于筒体，B 面属于机匣。计算方法的具体流程见图2。

图1 结构示意图Fig.1 Structural representation

图2 计算方法的具体流程Fig.2 The specific process of calculation method

1.1 基本条件

由于发动机的工况较多，全部计算工作量太大，因此选取发动机飞行包线过程中四种典型的恶劣工况，分别命名为：工况I、工况II、工况III、工况IV。四种工况的温度见表1。边界条件及其他设定如下：

表1 筒体、机匣的工作参数Tab.1 Working parameters of cylinder and casing

a)图1 中筒体装配所受载荷为周向螺栓总的正压力，具体值为69kN，受力方向为N1，受力面为D面；

b)筒体的内壁温度、保温层外壁温度见表1；

c)E面的换热系数根据经验取100W/m2℃；

d)机匣温度见表1；

e)以图1 中H 向为正，机匣所受载荷的转子轴向力见表1，轴向受力面为图1中C面；

d)各零件的材料及材料特性见表2和表3；

表2 材料特性Tab.2 Material characteristics

表3 1Cr11Ni2W2MoV导热率[6]Tab.3 Thermal conductivity of 1Cr11Ni2W2MoV

e)由空气造成的筒体内外表面的压力差忽略不计。

综合考虑以上载荷、温度等条件分别完成筒体、机匣变形计算。计算变形时首先需进行温度场计算，而后将温度场结果作为输入映射到结构计算过程中，即可开始结构变形计算，最终，结构变形的计算结果以表格的形式输出。

1.2 温度场计算

首先进行机匣的热分析[9]计算，计算时对零部件热边界进行较为合理的简化和划分是温度场计算结果准确的保障。根据流动腔室形状、空气系统提供的空气流动数据，以及E面换热取值，同时根据机匣的结构特点，将进气机匣按照不同直径的圆柱面划分12个不同的热边界，如图3 所示，用不同的颜色区分了相邻边界的界限。计算中的流动形式[10]包括环形腔道流动、静子强迫对流、没有明确气流流动[11]的微弱流动腔道以及轴承腔滑油对流。

图3 进气机匣热边界划分Fig.3 Inlet casing thermal boundary division

应用商业软件ANSYS 将材料数据和边界条件参数加载到二维模型中，计算得到工况I、工况II、工况III、工况IV下的机匣二维温度场分布如图4～7所示，云图中温度单位为K。

图4 机匣与筒体温度场分布（工况I）Fig.4 Temperature field distribution of casing and cylinder(Working condition I)

图5 机匣与筒体温度场分布（工况II）Fig.5 Temperature field distribution of casing and cylinder(Working Condition II)

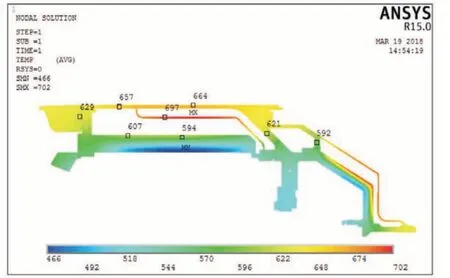
图6 机匣与筒体温度场分布（工况III）Fig.6 Temperature field distribution of casing and cylinder(Working Condition III)

图7 机匣与筒体温度场分布（工况IV）Fig.7 Temperature field distribution of casing and cylinder(Working condition IV)

1.3 结构变形计算

筒体的分网图见图8，将温度场结果输入映射到结构计算中，计算工况I、工况II、工况III、工况IV时热载荷综合影响下的变形[12-13]，得到A面相对于轴向约束面的变形量，结果见表4，表4 中所有值以逆航向为正。具体的变形量的云图见图8～图11。根据计算出的筒体变形云图，弹性密封环贴合端面的变形量不是常数值，可以证明一维的体积膨胀线性计算公式是不准确的。变形最大值列于表4[10]。

表4 变形分析结果Tab.4 Deformation analysis result

图8 筒体有限元分网模型Fig.8 Finite element mesh model of cylinder

图9 工况I变形云图（轴向位移,mm）Fig.9 Deformation cloud image of working condition I(axial displacement,mm)

图10 工况II变形云图（轴向位移,mm）Fig.10 Deformation cloud image of working condition II(axial displacement,mm)

图11 工况III变形云图（轴向位移,mm）Fig.11 Deformation cloud image of working condition III(axial displacement,mm)

图12 工况IV变形云图（轴向位移,mm）Fig.12 Deformation cloud image of working condition IV(axial displacement,mm)

2 间隙计算

采用相同的方法与步骤，可以得到机匣的轴向变形[14-15]，具体过程略去。只是在计算时需要按表1 中的轴向力带入图1中B面承受转子造成的正反向的2g载荷，并规定发动机逆航向为计算时的正向，逆航向变形量为正，反之变形量为负。计算得到机匣中B 面、F 面的变形的具体值见表5。由表5 可以很容易得到B 面对于F 面的相对变形量，结果见表6。由表6和表4可得到A面对于B面的相对变形量。取表6中的最大变形量的值，最终的计算结果见表7。

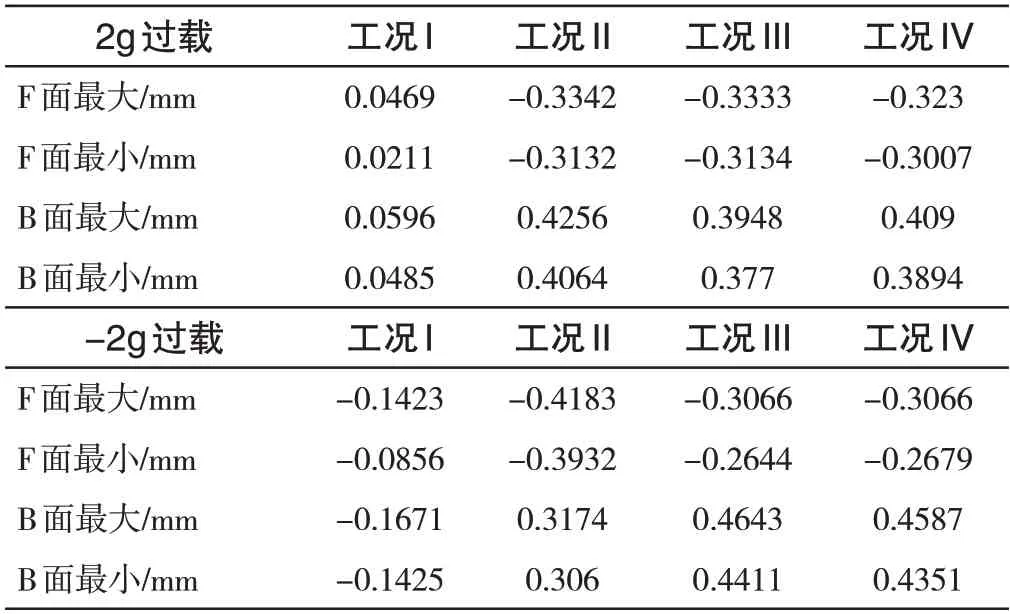
表5 B面、F面的变形量Tab.5 Deformation of plane B and plane F

表6 B面相对于F面的变形结果Tab.6 The deformation of plane B with respect to plane F

表7 A面相对于B面的变形极值Tab.7 Extremum of deformation of plane A with respect to plane B

3 结论

1）对零件的每一段边界进行精细化的预处理，可以计算得到较为精确的温度场计算结果。

2）根据筒体的变形和机匣的变形计算结果说明端面的变形量是非均匀的，证明了一维的线性计算公式不准确。

3）通过分别计算机匣和筒体的变形量，最后用差值的方法，得到了机匣相对筒体的变形量。为进一步评估压缩回弹对弹性密封安全性、可靠性的影响提供了依据。

4）本文所采用的计算方法具有通用性，可用于其他热变形计算中。