超高压海水泵水润滑轴承承载与散热仿真分析

王伟灿, 吴德发, 张 浩, 许锋炜, 吴世海, 高川琦

(1.华中科技大学机械科学与工程学院, 湖北武汉 430074;2.中国船舶科学研究中心深海技术科学太湖实验室, 江苏无锡 214062)

引言

近年来,水润滑轴承已广泛应用于水轮机、轮船艉轴和水上工作平台[1]。但是由于水黏度较低,当水润滑轴承处于低速、重载等特殊工况时,轴承与主轴间难以形成完整液膜[2-6],处于混合润滑甚至是干摩擦的润滑状态,导致轴承接触面磨损加剧[7]。不同于传统的金属轴承,新型水润滑轴承应用工程复合材料作为高性能材料,其可靠性及工作寿命得到了显著提高,适用范围也不断扩大[8]。此外,轴承结构也是影响轴承承载能力和使用寿命的重要因素之一,对轴承结构进行优化对轴承的工程设计和实际应用有着重要意义[9]。

目前,已有不少国内外学者对水润滑轴承的结构及承载能力进行研究。PAI R S[10-11]探究了无沟槽轴承、四直槽轴承、六直槽轴承的润滑性能和稳定性,结果表明,内表面带有沟槽的轴承,有助于外界流体流经轴承作为轴间润滑剂,提高轴承的润滑性能和稳定性;MALLYA R等[2,12]分析轴向沟槽水润滑轴承的结构对轴承整体承载能力和稳定性的影响,结果表明,当轴承沟槽使用较小的槽角时,轴承的承载能力和稳定性得到提高;王家序等[8]研究了轴承内表面微沟槽形貌对轴承承载能力的影响,结果表明,三角形微沟槽能够有效提高轴承的润滑性能。

目前有关水润滑轴承的研究,接触应力普遍较小(≤1 MPa),为提高超高压海水泵功率密度,需提高轴承载荷能力[13-15]。在大载荷(>5 MPa)作用下,轴承发热严重,热形变易导致卡死,过大轴间间隙会导致冲击增大。如何平衡该矛盾,需研究不同沟槽构形对轴承散热及轴承承载性能的影响。

本研究通过建立海水泵水润滑轴承承载与散热模型,对轴承内表面的散热及支撑进行仿真分析。探究沟槽数量不同对轴承接触应力、轴承变形和轴系散热的影响规律,综合静力学和热力学耦合变形仿真结果,确定轴承的沟槽形状和数量。

1 有限元模型

1.1 物理模型及网格划分

1) 物理模型

LIU F等[16]对沟槽构型进行对比发现,与直沟槽结构相比,螺旋槽结构使得轴承的应力分布更宽、系统跳动量更小。因此,本研究选用螺旋槽作为轴承的主要形构。4种轴承样本参数如表1所示。螺旋沟槽水润滑轴承模型如图1所示。其中,图1a为四螺旋沟槽模型、图1b为六螺旋沟槽模型、图1c为双向六螺旋沟槽模型、图1d为八螺旋沟槽模型。

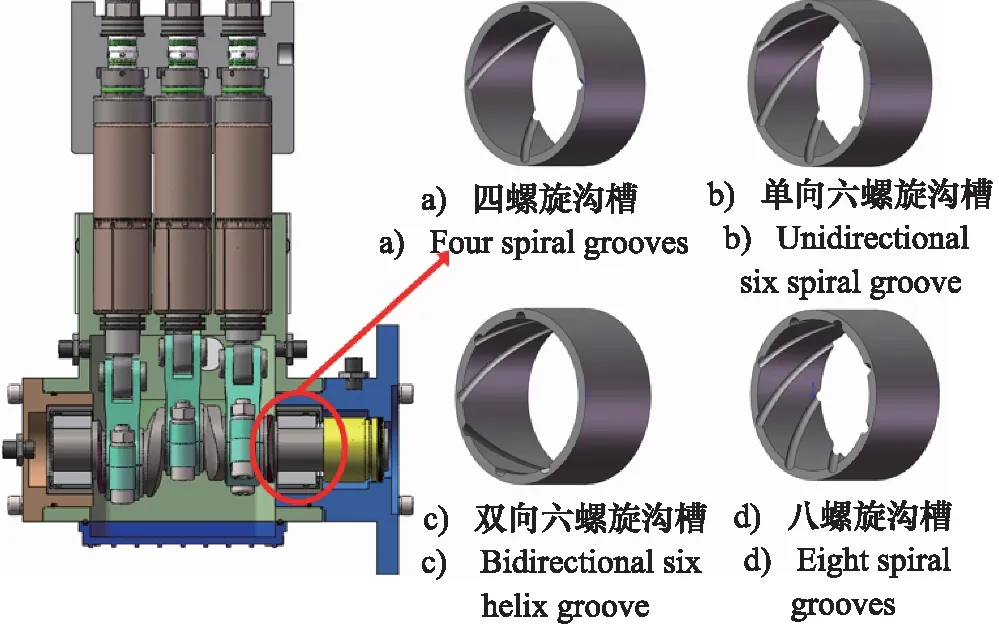
图1 螺旋沟槽的轴承结构Fig.1 Spiral groove bearing structure

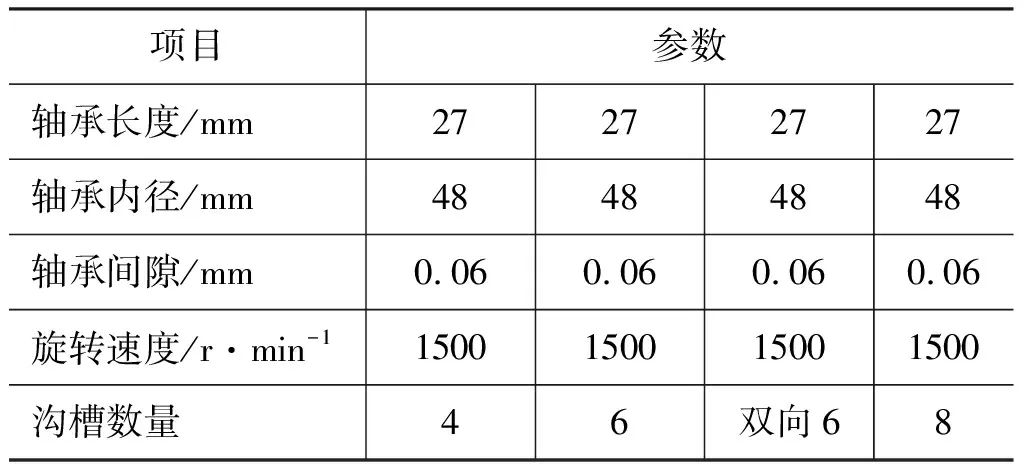
表1 水润滑轴承参数表Tab.1 Water lubricated bearing parameter table

2) 网格划分

图2所示为建立的水膜模型,采用六面体网格划分,网格节点数为900359,单元数为818685对比节点数为1503498的加密网格,端面流量相对误差不超过0.3%。为了得到精确的温度和速度梯度,在水膜截面处设置膨胀层,水膜厚度方向上分为10层,周向设置为0.03 mm网格。由于沟槽与水膜近壁面是相连结构,在水膜面与沟槽交汇面处设置平行网格,设置沟槽网格的最小尺寸为0.03 mm。

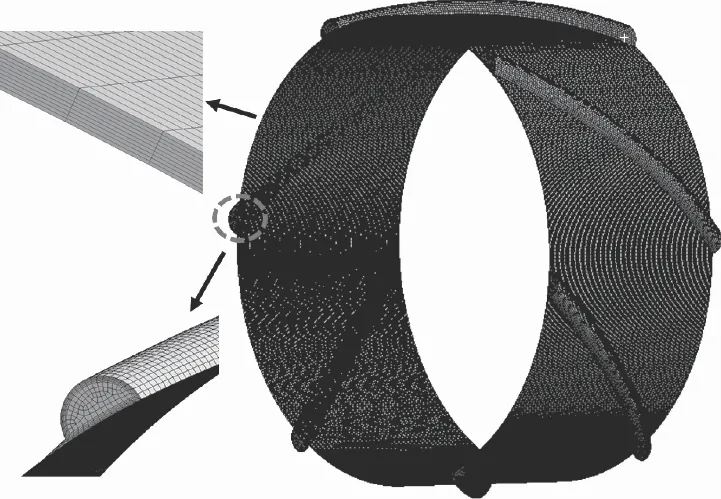
图2 水膜网格划分Fig.2 Water membrane meshing

图3所示为主轴轴承网格划分。设置轴承的整体网格尺寸为2 mm,并在轴承与轴的内部接触面进行额外细化尺寸,局部网格尺寸为1 mm。主轴与水膜接触面设为与水膜相同的六面体网格,其余非水膜接触面设为四面体网格,并检查无负体积网格。随后将主轴与轴承接触面设置为流固耦合面,主轴转速为1500 r/min,作用在轴承表面的轴承力为3000 N。

图3 主轴轴承的网格划分Fig.3 Meshing of spindle bearings

1.2 边界条件

如图4所示为水膜模型及边界条件示意图。在仿真计算中假设水为不可压缩的液体。在边界条件设置中,将水膜一端设置为压力进口,另一端表示为压力出口。默认轴承工作时完全浸入水环境中,两端面相对压力设置为0 Pa。将水膜外表面设置为静止表面,无旋转、滑移运动,水膜内表面设置为旋转表面,其旋转速度与主轴旋转速度相同,内表面无轴向滑移运动。

图4 水膜模型及边界条件设置Fig.4 Water film model and boundary condition setting

1.3 数值计算模型

数值计算采用Fluent中的k-ε模型作为数值计算模型,其湍动能k和耗散率ε方程的表达式如下:

(1)

(2)

式中,Gk为由平均速度梯度引起的湍动能;Gb为由浮力影响引起的湍动能;Ym为湍流脉动膨胀对总耗散率的影响;默认常值函数,C1ε=1.44,C2ε=1.92,Cμ=0.09;湍动能k和耗散率ε的普朗克常数σk=1.0,σε=1.3,在Fluent中可通过调节“黏性模型”面板来调整上述参数。

由于k-ε方程仅适用于离开壁面一定距离的湍流区域,因此在近壁面处应采用壁面函数对数值计算模型进行修正。假设在近壁面处,无量纲速度u*服从对数分布,其表达式如下:

习近平总书记亲自擘画的“八八战略”是浙江必须长期坚持的总纲领、总方略， 推进“‘八八战略’再深化、改革开放再出发”是省委着眼新时代提出的工作主线。“八八战略”为我们深刻领悟、精准把握新时期组织工作重大任务提供了战略方法和路径，我们一定要按照

(3)

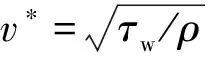
由于在上式定义中u*无法反应紊流脉动的影响,因此考虑到紊流脉动,将u*,y*扩展为[4]:

(4)

(5)

式中,cμ其中为涡动常数,通常;K为涡流动能;τw为壁面剪切应力;ρ为水流密度。此时近壁面速度的对数分布律为:

(6)

将近壁面速度表达式代入数值计算模型中进行修正,湍流耗散率εp按代数方程计算:

(7)

式中,yp为与湍流尺度对应的长度。

2 结果和讨论

2.1 沟槽构形对轴承内表面接触应力的影响

为探究相同工况下,沟槽构形及结构对轴承内表面最大接触应力σmax的影响。对沟槽构形不同的轴承结构进行静力学分析,得到如图5所示接触应力分布云图。

图5 不同沟槽构形下轴承接触应力云图Fig.5 Nephogram of bearing contact stress under different groove configurations

从仿真结果可知,在该工况下四螺旋沟槽轴承如图5a所示,最大接触应力为5.28 MPa,平均接触应力为0.61 MPa;八螺旋沟槽轴承如图5d所示,在该工况下所承受的最大接触应力是5.54 MPa,相较四螺旋沟槽轴承,最大接触应力约上升5%,平均接触应力为0.7 MPa。单向六螺旋沟槽轴承如图5b所示,在该工况下最大接触应力为5.44 MPa。相较八螺旋沟槽轴承,最大接触应力约减少3%,平均接触应力为0.63 MPa;双向六螺旋沟槽轴承如图5c所示,在该工况下最大接触应力为5.32 MPa,相较单向六螺旋沟槽轴承,最大接触应力约下降2%,平均接触应力为0.64 MPa,表面整体接触应力大小与四螺旋沟槽结构接近。

图6给出了轴承平均接触应力σd和轴承最大接触应力σmax随沟槽构形变化的规律。可以看出,双向六沟槽结构对减小轴承的最大接触应力效果非常显著。这是因为双向六沟槽结构相比单向六沟槽结构有效增大了轴承与主轴的接触面积,从而改善接触应力分布,减小应力集中。在相同工况下,对比另外3种单向轴承结构,发现随着沟槽数量增加,轴承最大接触应力有明显增大趋势,在沟槽数量为8时,达到最大值,而轴承整体平均接触应力随着沟槽数量的增加没有明显的变化,整体压力都低于PEEK材料的最大承压[17],论证了该轴承结构的可行性。

图6 沟槽构形对轴承最大接触应力和平均接触应力的影响Fig.6 Influence of groove configuration on maximum contact stress and average contact stress of bearing

2.2 沟槽构形对轴承耦合变形的影响

由于水的黏度低,水膜承载能力低,轴承在实际工况下的润滑状态为混合润滑,轴承内表面与主轴混合摩擦产生大量热。为探究沟槽构形对水润滑轴承散热性能的影响,对沟槽构形不同的水润滑轴承进行热仿真分析计算。在仿真计算中将主轴与轴承的接触面设置为流固耦合面,使用瞬态力学仿真模块计算出两者混合摩擦产生的发热量,并将结果导入流体仿真模块作为初始边界条件进行耦合仿真,此外将水膜以外的流体域设置为静态流体场,与水膜仅有能量交换,仿真结果如图7所示。图8给出了不同沟槽构形的轴承在稳定工作时轴承表面的最大温升T。可以看出随着沟槽数量提升,轴承表面温升呈下降趋势。四螺旋槽轴承温升最大,达到39.14 ℃;八螺旋沟槽轴承温升最小,约为24.78 ℃;曲线在双向六沟槽处稍有上升,达到36.43 ℃,这是因为双向六沟槽轴承为了实现泵腔内部流体循环,在单方向上可视为只有三沟槽散热,加上轴承承载部位无沟槽分布,流体无法对发热部位进行直接散热,导致其散热性能相比单向六沟槽轴承降低了18%。

图7 不同沟槽构形下轴承温升云图Fig.7 Cloud image of bearing temperature rise under different groove configurations

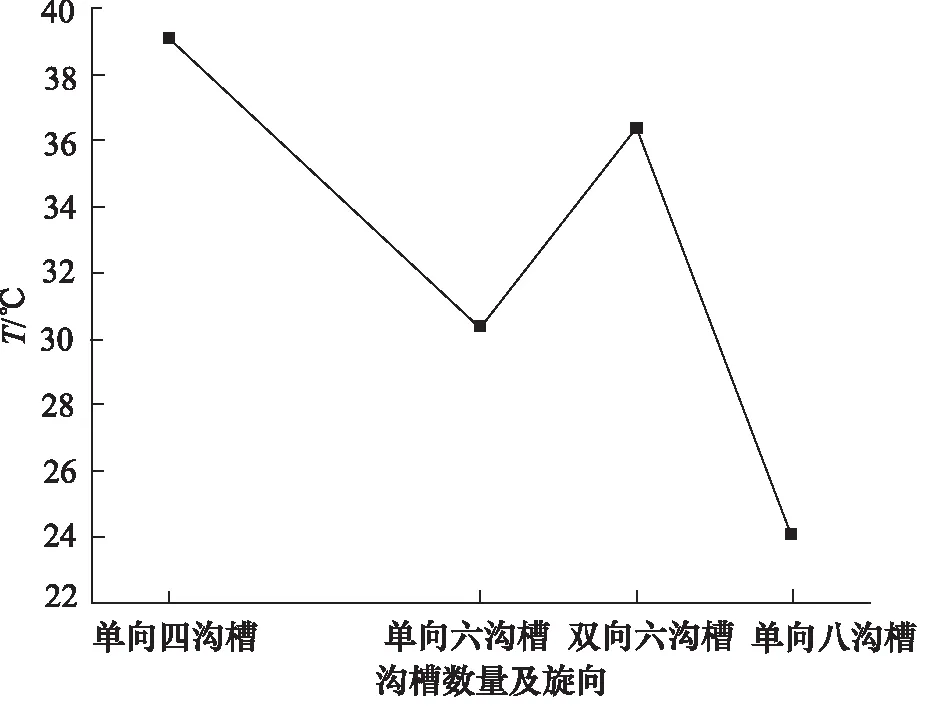
图8 沟槽数量对轴承最大温升的影响Fig.8 Effect of groove number on bearing maximum temperature rise

将热仿真所得的结果和静力学计算结果进行耦合计算,模拟轴承在实际工况下流固耦合变形,结果如图9所示。通过对仿真结果分析,四螺旋沟槽轴承如图9a所示,最大变形量lmax为3.3×10-3mm,平均变形量ld为3.8×10-4mm;八沟槽轴承如图9d所示,最大变形量是3.7×10-3mm,相较于四螺旋沟槽上升约为12%,平均变形量为4.5×10-4mm;单向六螺旋沟槽轴承如图9b所示,最大变形量是3.4×10-3mm,相较于八螺旋沟槽轴承下降约10%,平均变形量为4.2×10-4mm;双向六沟槽轴承如图9c所示,最大变形量是3.2×10-3mm,相较于单向六沟槽轴承下降约6%,平均变形量为4×10-4mm。

图9 不同沟槽数量下轴承耦合变形云图Fig.9 Bearing coupling deformation cloud image with different number of grooves

图10给出了轴承最大变形量和平均变形量随沟槽数量变化的规律。从图中可以看出,相同工况下对比4种轴承结构,随着沟槽数量的增加轴承最大变形量和平均变形量均有明显上升趋势。在沟槽数量为8时,轴承变形量最大。而双向六沟槽结构相比于其他沟槽结构变形量较小,这也证明该结构有效增加轴承受力面积,能显著减小变形量的同时,也能提供良好的散热,最终表现出优越的抗变形能力。

图10 沟槽数量对轴承最大变形量和平均变形量的影响Fig.10 Influence of number of grooves on maximum and average deformation of bearings

3 结论

通过有限元计算,分析了水润滑轴承内表面不同数量、不同流向的沟槽对轴承工作时最大接触应力、最大温升、最大变形量的影响。仿真结果表明,在轴承内表面设置沟槽能够对轴承起到有效的散热作用,且随着沟槽数量的增加,散热作用也有明显改善。在相同工况下,单向八螺旋槽轴承的最大温升相较于单向四螺旋槽轴承下降36.7%。但是沟槽数量增加的同时,轴承内表面形变量也随之增加,单向八螺旋槽轴承的最大变形量相较于单向四螺旋槽轴承增加12%。因此,综合考虑轴承的散热和变形量,设计双向六螺旋沟槽轴承。其最大温升相较于单向四螺旋沟槽轴承下降7%,且变形量较单向八沟槽轴承减少约12%,表明该结构在提升腔内流体循环散热作用的同时,对减少轴承变形起到显著效果。