基于速度偏差补偿的车载跟瞄系统自抗扰研究

祝军生, 方志耕, 金小琳, 任 维

(1.南京航空航天大学经济与管理学院, 江苏南京 210016; 2.中国航天科工集团八五一一研究所, 江苏南京 21007; 3.润坤(上海)光学科技有限公司,上海 201100)

引言

光电跟瞄系统是由精密两轴转台、快反镜、光电探测器、驱动系统等组成,主要用于对目标的跟踪与瞄准。在火炮控制、导弹发射、舰船和飞机的自动驾驶激、光对抗等领域有大量的应用。光电跟瞄多采用粗精复合轴的控制策略,以达到微弧度的跟踪与瞄准精度,同时使用场景要求系统处于固定水平地面上,以减少外界振动对跟瞄精度的影响。随着运动平台下光电跟瞄的应用需求拓展,如何保证在车载运动平台下实现微弧度级跟瞄精度是目前亟需解决的难点。

光电跟瞄系统具有大转动惯量、强非线性摩擦的特点[1],此外,还面临质量不平衡力矩、车载振动力矩的影响。为了满足系统的响应速度和跟踪精度要求,主要通过提高系统型别和低频增益的方式实现,这种处理方式的特点将原本的非线性对象特性线性化,采用基于频域Bode图的控制设计方法,可以在带宽、鲁棒性、跟踪精度、响应速度等方面取得良好的平衡,在实际工程中也应用广泛。

然而在运动车载平台下,光电跟瞄系统随着载体的加速、减速、匀速、拐弯、爬坡、下坡、横滚、倾斜等状态的改变,光电跟瞄系统的对象特性变化显著,振动幅度和频率复杂。其中车载振动对光电跟瞄系统的影响远大于非线性摩擦和对象特性的摄动的影响。

高带宽意味着高增益和高抑制比。但系统的带宽受限于系统的机械谐振,无法进一步提高。多年来学者通过从扰动补偿的角度出发进行深入的研究,比较有代表的是基于扰动测量的前馈补偿和构造扰动观测器进行扰动前馈补偿两类方法。载体扰动测量传感器所决定的测量坐标系与基准坐标系间由安装带来的误差将影响前馈的补偿能力。这些安装误差包括轴系间的不正交、安装底面的不平等。而扰动观测器在不需要增加额外传感器的基础上,利用标称模型估计出扰动并前馈补偿,然后扰动观测器的估计补偿精度依赖于标称模型的准确度。若要提升控制效果,需要建立较为准确的非线性摩擦力模型[2-3],或针对系统扰动观测器输入进行Kalman滤波[4-5]等方法,增加了系统建模的难度及计算复杂度。非线性自抗扰控制(Active Disturbance Rejection Control,ADRC)[6-7],利用跟踪-微分器(TD)得到微分信号及安排过渡过程,利用线性扩张状态观测器(Linear Extended State Observer,LESO)估计出实时的系统状态与系统总扰动,非线性状态误差反馈控制律(Nonlinear Law State Error Feedback,NLSEF)实现非线性状态与扰动反馈,进而实现扰动的主动抑制[8]。由于非线性ADRC工程化应用中存在参数较多且参数整定困难的问题,高志强等将非线性ADRC简化为线性LADRC结构,并提出“带宽法”的参数整定方法,进一步降低参数个数及参数整定难度[9]。自抗扰方法同时广泛与其他控制技术相结合,变增益自抗扰[10]、自抗扰与重复控制[11]、自抗扰与模型补偿控制[12-13]、自抗扰与反步积分法[14]均得到了广泛应用。

针对上述问题,本研究提出了一种基于速度偏差补偿ADRC控制方法,该方法能减小LESO状态估计压力,提高估计精度。同时将速度回路输入与陀螺输出之间的偏差信号,引入到LESO中进行补偿,从而提高系统的扰动抑制能力及速度响应特性。

1 系统建模与扰动分析

光电跟瞄系统的粗跟踪系统的执行机构为二自由度旋转转台,精跟踪系统的执行机构为高动态响应的快反镜。车载平台首先影响的是粗跟踪系统,根据系统指标分配要求,粗跟踪在车载平台下的跟踪精度要不大于1 mrad,才能保证精跟踪的闭环后能达到微弧度级的跟踪精度[15-16]。因此本研究以转台为研究对象,对其进行建模分析,车载光电跟瞄系统等效物理关系如图1所示。

图1 光电跟瞄系统等效物理关系图Fig.1 Equivalent physical relationship diagram of photoelectric gimbal

在不考虑高阶机械谐振的情况下分析转台的特性,即认为负载与电机间的刚度系数无限大,其不考虑摩擦与阻尼的影响,电机的角位移等于负载的角位移,即θm=θL。根据电机的力矩平衡方程式,有:

(1)

式中,Jm—— 电机的转动惯量

θm—— 电机的角位移

Ma—— 电机的电磁力矩

电机的电磁力矩Ma等于电枢回路电流Ia和力矩系数Cm的乘积,即:

Ma=CmIa

(2)

根据电压的平衡方程式有:

(3)

(4)

式中,Ua—— 功率放大器提供给电机的电枢电压

Ue—— 电机的反电势

Ra—— 电机电枢回路电阻之和

Ia—— 电机电枢回路内电流

La—— 电机电枢回路电感之和

Kb—— 电机的反电势系数

对式(1)～式(4)进行合并拉氏变化处理,可得电枢电压与电机转速之间的传递关系:

(5)

式中,JL—— 负载的转动惯量

式(5)说明转台的低阶特性可以看作由2个惯性环节串联构成,取决于转台的转动惯量、力矩系数、电枢电路参数。由于负载导致的高阶谐振环节直接限制平台的伺服带宽,一般高于50 Hz,不用对其估计和补偿。对光电跟瞄系统伺服指标影响最大的还是其轴系摩擦力矩、质量不平衡力矩和外界干扰。

1.1 摩擦力矩

转台的方位和俯仰轴承内环与轴采用小间隙配合,轴承外圈与轴承座选用过渡配合,不可避免存在摩擦。对于转台这种标准的机械运动机构,转台制动时要克服最大静摩擦力,其在低速状态下随着速度的增加变小,表现为与速度相关的连续函数。该摩擦模型可以用LuGre摩擦模型进行描述:

Tmf=fc+(fs-fc)e[-(v/vs)δ]+fvv

(6)

式中,fs—— 最大静摩擦力矩

fc—— 库伦摩擦

fv—— 黏滞摩擦

vs—— Stribeck特征速度

vs,δ—— 经验常数

此外,在大量工程实践中观察到实际的摩擦力矩也会由于不同的旋转方向而有所不同。外界温度的变化、轴承的润滑状态和磨损程度都会使得摩擦力大小表现的不一样,这种较强的非线性摩擦特性,难以建立模型准确补偿。

1.2 质量不平衡力矩

由于加工误差和装配误差的存在,转轴搭载的负载重心与转轴的中心存在一定程度的偏离,进而产生质量不平衡力矩,其数学表达公式如下:

Tmb≈mgβsin(α0+θ)

(7)

式中,m—— 等效不平衡质量

g—— 重力常数

β—— 等效不平衡质量重心到转轴中心的距离

α0—— 等效不平衡质量重心和转轴中的连线与测试轴重心之间的夹角的初始值

θ—— 质量不平衡重心和转动中心轴的连线与测试轴重心之间的夹角

1.3 外界干扰力矩

外界干扰力矩在某种程度可以等效为负载力矩的变化,而光电跟瞄系统面临的外界干扰力矩主要来自于运动载体的振动。运动载体的振动特性与载体的应用场景密切相关,既有周期性振动,也有冲击振动。振动的幅值和频率都有所不同。在工程上,优先考虑添加空气弹簧减振器进行被动隔离。隔振系统的固有频率一般在3～4 Hz,10 Hz左右处振动隔离能力达80%,20 Hz振动隔离能力达99%。因此对光电跟瞄系统影响最大的还是4 Hz以下的大角度振动。

2 传统LADRC控制系统设计

本研究的二阶被控对象模型可描述为:

(8)

由于实际运用中对控制量增益b估计不准,自抗扰的基本原理是将对象模型进行了重新构造,将不准的扰动扩张到包含内扰和外扰的f(y,ω,t)中:

(9)

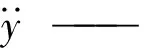
u—— 被控对象输入

ω—— 扰动

f—— 总扰动

选取状态变量:

(10)

式中,x1,x2,x3,h—— 状态变量

L—— 观测器误差反馈增益矩阵

将上述状态方程改写为线性扩张状态观测器形式:

(11)

则线性状态误差反馈控制律(LSEF)表现为:

u0=kp(r-z1)-kdz2

(12)

式中,r—— 给定值

kp,kd—— 控制器增益

再将线性LADRC简化为一般控制回路形式,如图2所示。

图2 LADRC的等效控制回路Fig.2 Equivalent control loop of LADRC

其中,C1和C2的表达形式如下:

(13)

(14)

结合式(9)可得:

(15)

(16)

(17)

(18)

由上式易知,ADRC为积分串联型控制器,增加积分环节可以减小系统的稳态偏差,并且ADRC将模型偏差等考虑入总扰动中,具有较强的鲁棒性且在型号中具有较好的适用性[17]。状态观测器LESO为自抗扰控制器核心,可以综合估计出系统的内扰、外扰,直接影响自抗扰控制器的抗扰能力。然而当系统受较大扰动时,自抗扰控制器会存在幅值和相位的跟踪偏差,影响整体系统跟踪效果及振动抑制能力[18-19]。

3 基于速度偏差补偿的LADRC设计

摩擦力矩、质量不平衡力矩与转台动作状态、加工误差、机械装配等相关,具有不确定性且无法实时测量。设备车行进过程中振动产生的外扰动以及转台振动则可以通过陀螺仪等直接进行测量。因此,本研究以陀螺仪作为传感单元提出了一种基于速度偏差补偿的LADRC设计方法,其控制回路结构见图3。

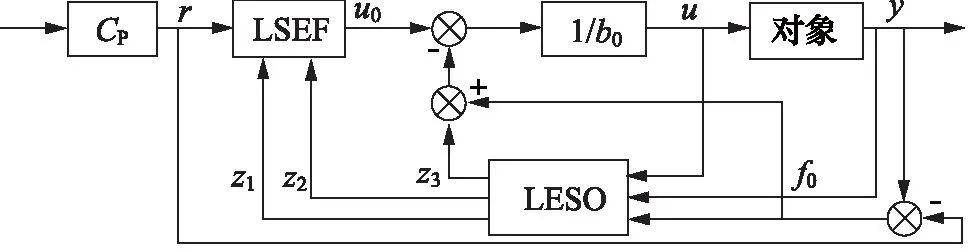
图3 基于速度偏差补偿的LADRC控制回路Fig.3 LADRC control loop based on speed deviation compensation

基于经典自抗扰状态观测器LESO,将速度偏差补偿引入到观测器中进行重构,得到基于速度偏差补偿LADRC的线性扩张状态观测器形式:

(19)

由此,推导出状态反馈控制律LSEF表达式为:

u0=kp(r-z1)-kdz2

(20)

(21)

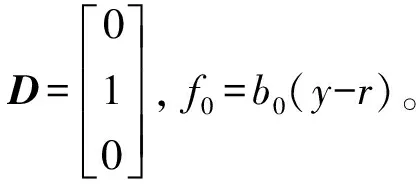
由于ADRC具有需调参的参数多、整定难度大等难点。根据“带宽法”参数整定方法,在观测器LESO的-ω0处配置极点,ωc为控制器带宽。将L,kp,kd参数简化为:

3.1 跟踪特性分析

对速度偏差补偿LADRC控制器的跟踪性能进行分析。定义速度跟踪误差e=r-y,结合状态观测器及反馈控制率,可得:

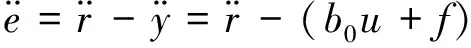
(22)

由上式所示,f为系统所受内扰、外扰总和,由扰动观测器LESO估计扰动z3及速度偏差补偿f0两部分共同抵消。f0通过传感器测量将速度偏差补偿到观测器LESO及控制率LSEF中。由于转台低频受到摩擦扰动、质量不平衡力矩等非线性扰动对系统影响较大,使用速度偏差补偿可以有效分担LESO对扰动观测的压力,并提高跟踪精度。将上式进行拉氏变换,得:

(23)

由上式可知,当输入信号为阶跃信号时,系统的稳态跟踪误差为0,满足转台速度环快速响应、无差跟踪的要求。

3.2 扰动抑制特性分析

一般形式控制结构中的C1和C2的表达式如下:

C1=(b0+kp)s3+(b0kd+b0l1+kpl1)s2+(b0kp+b0l2+kpl2+b0kdl1)s+kpl3/[b0s3+(l3+b0kd+b0l1+kdl2+kpl1)s2+(b0kp+b0l2+kdl3+kpl2+b0kdl1)s+kpl3]

(24)

C2=b0s3+(l3+b0kd+b0l1+kdl2+kpl1)s2+(b0kp+b0l2+kdl3+kpl2+b0kdl1)s+kpl3/[b0s3+(b0kd+b0l1)s2+(b0kp+b0l2+b0kdl1)s]

(25)

结合式(9),可得:

(26)

(27)

(28)

4 试验验证

为验证本研究所提基于速度偏差补偿的ADRC控制策略对扰动抑制效果,在光电跟瞄系统上,针对转台速度环进行实验验证。光电跟瞄实验平台如图4所示,包含有光电跟瞄转台、运动控制板、电源、角度编码器和陀螺仪等。

图4 光电跟瞄实验平台Fig.4 Photoelectric tracking and aiming experimental platform

为验证本研究提出的速度偏差补偿的LADRC方法效果,将其与经典线性自抗扰、PID闭环控制效果进行对比仿真。分别针对转台电机转速n输入阶跃、正弦信号,从时域和频域进行仿真分析。

如图5所示,在0.05 s时,输入阶跃信号;在0.35 s时,对系统施加外扰动。可以看出,速度偏差补偿LADRC相比于经典自抗扰和PID控制,能够更快的响应且快速稳定。当系统受到外扰动时,经典自抗扰与速度偏差补偿LADRC抗扰动能力明显优于PID控制,且速度偏差补偿LADRC具有更强的扰动抑制能力。

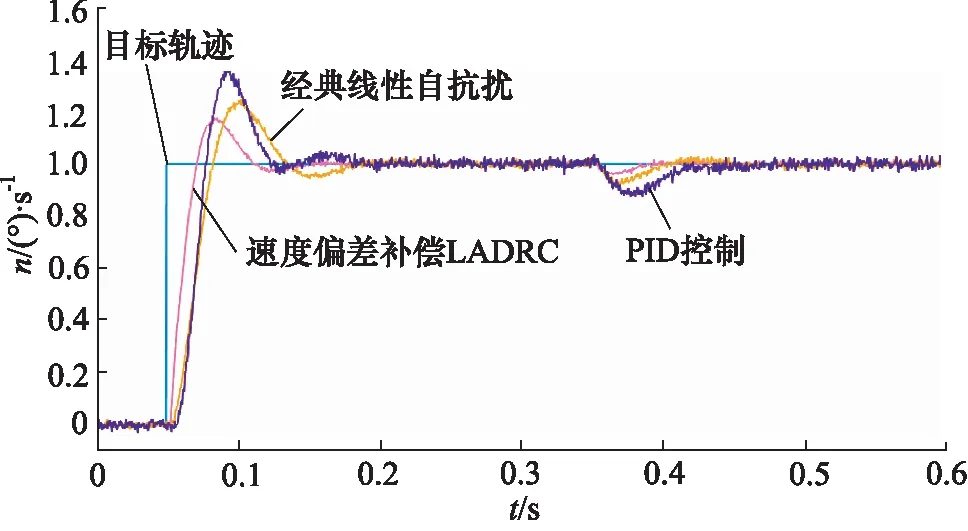
图5 阶跃信号跟踪效果对比Fig.5 Step signal tracking effect comparison

如图6所示,当输入信号为正弦信号时,由于摩擦力矩影响;在输入目标速度过零即转动方向变换时,会有明显“低速爬行”现象。相较于经典自抗扰及PID控制方法,速度偏差补偿LADRC具有更好的跟踪效果。速度偏差补偿LADRC可以更好的将系统模型偏差进行补偿,具有更好的普遍适用性。

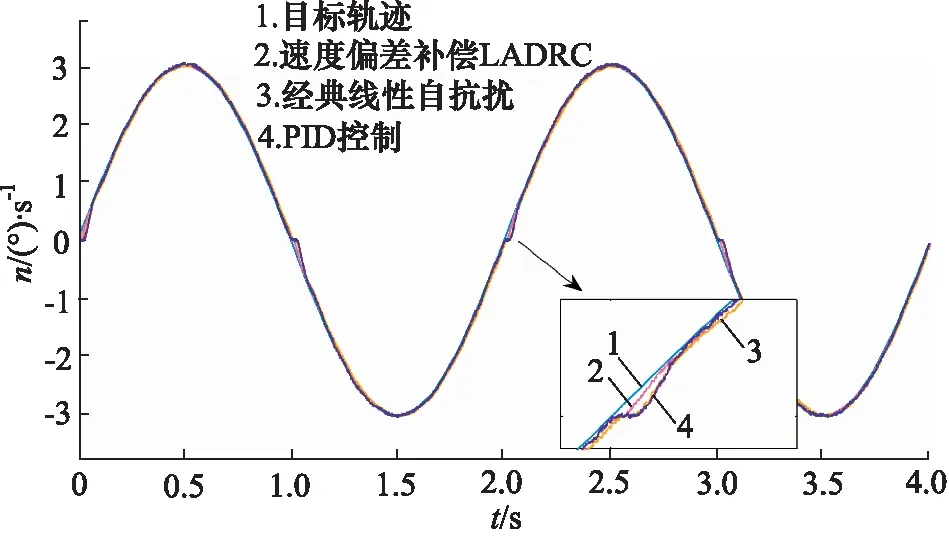
图6 正弦信号跟踪效果对比Fig.6 Sine signal tracking effect comparison

如图7所示,在跟踪输入的正弦信号基础上,加入了外扰动。速度偏差补偿LADRC、经典自抗扰、PID 3种方法的跟踪偏差均方差分别为0.04086, 0.08853, 0.09611。速度偏差补偿LADRC对外扰动的抑制能力明显高于PID及经典自抗扰方法。

由图8可知,速度偏差补偿LADRC相对于经典自抗扰以及PID,能够提升闭环带宽并降低超调;将系统速度环闭环带宽从13 Hz提升到18 Hz。

如图9所示,通过上图可明显看出3种方法对外扰动抑制能力,速度偏差补偿LADRC对外扰抑制能力远高于PID方法;在0.1～10 Hz的低频范围中,对扰动的抑制能力提高了10 dB。

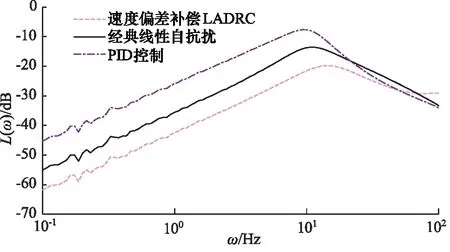
图9 扰动抑制频域对比Fig.9 Disturbance rejection frequency domain comparison

5 结论

本研究以光电跟瞄系统为研究对象,从摩擦力矩、质量不平衡力矩、外界干扰力矩等方面分析系统受到的内扰及外扰, 在转台速度环中引入二阶线性自抗扰控制方法。并在此基础上,提出了一种基于速度偏差补偿的自抗扰控制方法, 该方法将速度输入和速度输出之间的偏差作为一个新的误差源,重新引入到ESO中进行一步补偿,提升了LADRC非线性扰动抑制能力,同时减轻LESO观测压力实现快速稳定跟踪要求。其参数整定方式与标准二阶线性ADRC一致,简单易用。最后的试验表明,基于速度偏差的ADRC与标准ADRC和PID控制器,有更高的跟踪精度和扰动抑制能力。