基于确定性因子模型的区域地面沉降敏感性研究

伊尧国，田秋媛，崔 楠，王奕珺

（1.天津城建大学地质与测绘学院，天津 300384；2.昆明理工大学国土资源工程学院，昆明 650093；3.北京师范大学遥感科学国家重点实验室，北京 100875）

地面沉降又称为地面下陷，是由地下松散地层压缩固结，导致地壳表面高程降低的一种地质灾害，目前在世界各地普遍存在.针对这一问题，国内外学者对其形成机理、致灾因素、监控措施等方面进行了相关探讨和研究.朱邦彦等[1]利用熵权法对地下空间非均匀沉降引起的地下空间结构的安全效应进行了综合评估；张荐铭等[2]通过GIS 三维分析方法提取出昆明市地表形变整体情况，总结出昆明市地表形变的沉降规律和变化特点；张双成等[3]利用合成孔径雷达干涉测量技术对北京2017—2020 年区域地面沉降的时空分布特征进行了探讨；杜东等[4]利用PS-InSAR 技术，结合高精度GPS 数据，开展了地面沉降特征及其影响因素研究；Majid 等[5]应用随机森林的机器学习方法研究地面沉降的敏感性；Ali Ranjbar 等[6]论证了地下水过采导致土层的不规则空间分布从而引起地面沉降和建筑物的破坏；Zhou 等[7]将RELAX 与PS-InSAR技术相结合，改进了对地面沉降持续散射体的识别；Zhang 等[8]基于InSAR 数据实现了对地面沉降监测及地下含水层的参数反演；Teijevander 等[9]通过对Sentinel-1A 数据连续散射干涉时间序列进行分析，得到了仰光定居点沉降灾害的范围及危险性程度；Ghorbanzadeh等[10]采用自适应神经模糊推理系统和交叉验证方法进行地面沉降敏感性研究.

很多研究成果表明，地面沉降产生和发展是一个复杂的非线性系统[11]，只有在分析模型中选取对于地面沉降发生具有显著影响作用的影响因子，才会获得较好的预测结果.另外，由于其涉及土壤的压缩变形，以及地下水的渗流特性等因素，这些因素都具有随机性、模糊性和不确定性，因此，应用普通的数理模型很难建立一个适合的预测模型来对其进行敏感性分析与评价.

天津市作为我国地面沉降现象出现比较早的地区之一，近些年随着滨海新区的快速发展建设，以及对地下水、地热、石油、天然气等地下资源的不断开发，使得该地区的地面沉降问题愈发严重.明确沉降产生的主要原因，并对其产生的敏感性及发展趋势进行准确的评估和预测，将对该地区今后的经济发展和社会生活具有十分重要的意义. 本文基于天津市滨海新区野外水准监测得到的研究区沉降数据，选取了导致地面沉降产生的4 个最重要的影响因子，通过确定性因子模型对该区域地面沉降发生的敏感性进行了研究，并分析其产生的主要影响因素及未来发展趋势，从而总结出该区域地面沉降的时空演化规律.

1 研究区与数据源

天津市地面沉降的问题由来已久，20 世纪50 年代至80 年代初，天津地面沉降主要是由地下水过采所导致的，进入90 年代以来，地下水开采受到一定程度的控制，水位变动幅度减小，地面沉降现象基本上呈现为微量下沉态势[12].但是近几年随着天津滨海新区的建设发展，该地区又呈现出新的更加严重的沉降趋势. 本文研究区就选取的是天津市滨海新区（见图1），研究区的地理位置位于海河流域的下游，总面积2 270 km2，地理位置在38°40′N—39°30′N，117°00′E—118°20′E 之间.地貌类型属于冲积海积平原，从地质学角度来看，该区域位于海河断裂带与沧东断裂带之间，地质条件比较稳定[13]，因此由地质构造变异引发的地面沉降在这一区间相对较小，因此本文将研究重点放在地下水开采以及建筑群密集荷载引发的地面沉降上面.

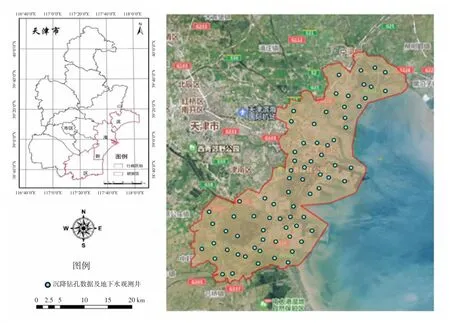
图1 研究区地理位置

实时准确的遥感影像和基础地理数据是对地面沉降进行计算和分析的依据[14]，因此，本文搜集了研究区最近10 年的相关数据，其中包括1 ∶2 000 地质勘探图；1 ∶1 000 实测地形图；研究区内均匀分布的48个地面沉降钻孔数据及地下水观测井监测数据，采用克里金插值方法将48 个钻孔点的沉降相关数据进行空间插值得到其在研究区内的空间分布情况，并选取与地面沉降关系最为密切的4 个因子，即地下水渗透系数、地下水埋深、压缩层厚度、压缩模量，绘制出空间分布专题图（见图2），再通过ArcGIS10.8 软件的重采样功能将上述专题图转换为1 m×1 m 分辨率的栅格单元，构建沉降分析空间数据库，以便从中提取影响区域地面沉降的各因素的地理信息，并以此来直接或间接地分析地下水开采以及建筑群荷载引发的地面沉降的敏感性问题[15].

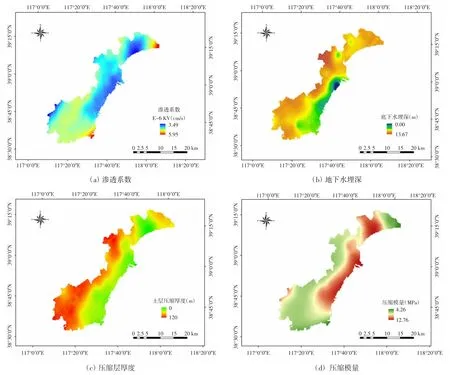
图2 沉降影响因子空间分布专题图

2 地面沉降敏感性评价

2.1 确定性因子模型

确定性因子模型（CertaintyFactorsModel）由Shortliffe和Buchanan 提出，后来经Heckerman 进行改进，是使用确定性因子处理不确定性问题的一种概率统计方法，广泛应用于医学、地学、环境等学科的定量分析与计算当中，使用该模型同样可以对地面沉降的敏感性进行分析和研究.该模型应用在地面沉降计算中的核心思想是计算已知沉降点在其中某个影响因子子类中发生的概率值和在整个研究区范围内发生的概率值，然后依据公式（1）分别计算各个沉降影响因子的CF（Certainty Factors）值，从而定量化地分析每个影响因子对沉降发生的敏感性程度，并预测未来沉降发生的可能性大小[16].

公式（1）中：PPa 代表地面沉降在其中的某个影响因子子类中发生的概率；PPs 是地面沉降在整个研究区范围内发生的概率.而在具体的计算当中，PPa 表示为代表某一影响因子子类中存在的沉降发生的数目与这一子类的单元栅格总数的比值；PPs 表示在整个研究区范围内的沉降发生的数目与研究区所有栅格总数的比值.

地面沉降的产生是该地区各种相关致灾因子综合作用的结果.因此，在分析该区域内地面沉降分布规律及其特点时，采用确定性因子模型可以比较容易地解决作为自变量的沉降影响因子如何量化问题，即多源异质数据的融合问题[17]，这一点可以通过计算沉降降影响因子对沉降的CF 值具体体现出来，进而非常直观地找出影响地面沉降发生发展趋势的关键性因子.

2.2 沉降影响因子提取与计算

对于空间数据库中每一个沉降敏感性影响因子数据层，首先将其按一定规则划分为不同的级别，然后基于GIS 的空间分析方法，将每个数据层与野外实测得到的地面沉降数据层进行叠加分析，计算研究区内沉降数目与各个因子子类的单元栅格总数的比值，以及沉降数目与研究区所有栅格总数的比值.

CF 值的取值范围在-1 与1 之间. 如果CF 值为正，就表示发生沉降事件的确定性高，即发生沉降的可能性大；如果CF 值为负，就表示沉降事件发生的确定性低，即发生沉降的可能性小；如果CF 值接近0，就说明不确定沉降事件是否会发生[18].

2.2.1 渗透系数

地下水流渗透通过土层的性能，被称为地下水的渗透性.地下水渗透系数大的土层，如砂土层，超静孔隙水压力会很快消散，地下土的压缩速度快，压缩量比较小；相反，对于地下水渗透系数小的土层，如粘性土层，土的透水性相对比较弱，超静孔隙水压力的消散会比较缓慢，就要经历非常长的时间，地下土的压缩才可以完成，最终的压缩量就比较大[19].因此，根据有效应力原理对地面沉降进行研究时，地下水的渗透系数决定了超静孔隙水压力的缩减速度，也决定了沉降量的大小.

对于天津滨海新区广泛分布的饱和粘性土来说，由于其透水性弱，在应力作用下超孔隙水压力消散较慢，土体的压缩经常需要较长的时间才能完成，其压缩量越大，产生地面沉降的可能性就越大.因此，地下水的渗透系数是分析沉降敏感性一个非常重要的因子[20]. 本文依据研究区不同土层中水的渗透特征对地下水的渗透系数进行分级（见表1），从而分析不同地下水渗透性分级区间对沉降敏感性的影响.

表1 渗透系数分级及CF 值确定表

从表1 的计算结果可以发现，在研究区内地面沉降发生较频繁的渗透系数范围位于[3.49，3.57]×10-6kV（cm/s）区间，这一区间正是黏性土层所在的渗透系数区间，是地面沉降的易发区；而研究区内局部区域分布的砂土层，由于渗透系数值较大，经计算，其CF 值较小，不易于沉降的发生.由此可见，地面沉降的大小和速率不但取决于渗透系数的大小，而且更主要的取决于所在区域土壤性质，分析得出，黏性土比砂土更易于沉降的产生和发展.

2.2.2 地下水埋深

一般所称的地下水是指地下潜水，潜水埋藏深度指的是潜水面与地面的距离，即地下水埋深.从地下土壤受力的微观角度来分析，饱和土体的压缩过程与超静孔隙水压力的消散过程是一致的，在饱和粘性土中，地面沉降量的大小除了与其含水量、密度、孔隙比、饱和度等物理性质指标相关外，地下水埋深也是影响地面沉降的比较重要的一个因子[21]. 本文根据研究区不同土层深度孔隙水压力的力学性质对地下水埋深进行分级（见表2），从而分析研究区不同地下水埋深区间对地面沉降敏感性的影响.

表2 地下水埋深分级及CF 值确定表

从表2 的计算结果可以发现，在研究区内地面沉降发生较频繁的地下水埋深范围位于（130，170]m 区间，这一区间是地面沉降的易发区.

2.2.3 压缩层厚度

土壤压缩层是指在地面动静荷载的作用下，地基土中产生沉降的土层总和.压缩层厚度越大，土体可以被压缩的空间越大，就越容易产生沉降；反之，如果压缩层厚度越小，土体可以被压缩的空间越小，就越不容易产生沉降，因此，压缩层厚度也是影响地面沉降的比较重要的一个因子[22].本文根据研究区地质剖面图中不同地下土层的物理性质对压缩层厚度进行分级（见表3），从而分析研究区内不同压缩层厚度区间对沉降敏感性的影响.

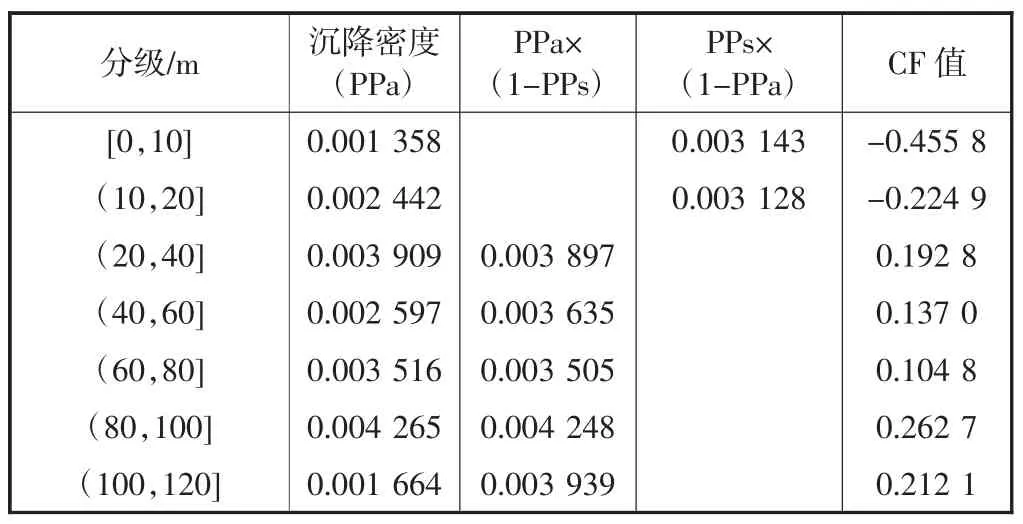
表3 压缩层厚度分级及CF 值确定表

从表3 的计算结果可以发现，研究区的压缩层厚度范围在（80，100]m 区间内的CF 值最大，说明这一厚度区间极易发生沉降.

2.2.4 压缩模量

压缩模量是指土在有侧限条件下受压时，土的竖向应力变化量与其相应的竖向应变变化量之比，它是计算地面沉降的一项重要参数.研究区广泛分布着第四纪粉质粘土和淤泥质土，这种土的物理特性决定了它是一种高压缩性的土壤，承受上部荷载的能力较差，因此，在地下30 m 以内的浅表土层，会引起较大的沉降量[23].本文根据研究区地质剖面图中不同地下土层的物理性质对土层压缩模量进行分级（见表4），从而分析研究区内不同土层压缩模量区间对地面沉降敏感性的影响.

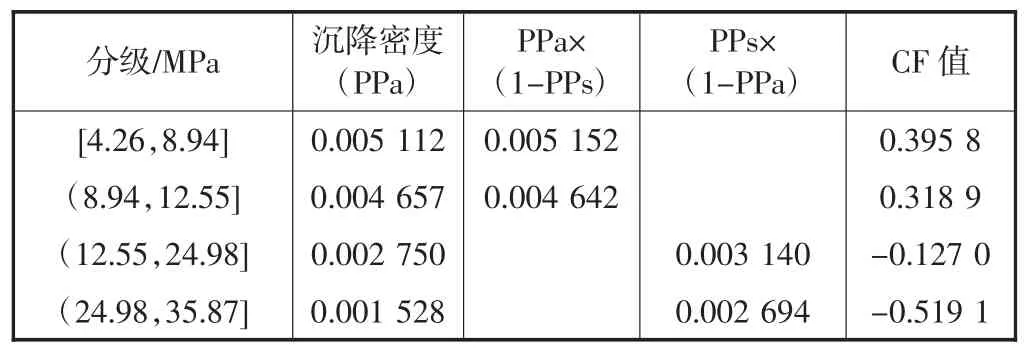
表4 压缩模量分级及CF 值确定表

从表4 的计算结果可以发现，研究区的压缩模量范围在[4.26，8.94] MPa 中CF 值最大，这一区间正是黏性土和淤泥质土所在的压缩模量区间，较易发生沉降；而研究区内其他局部较小区域分布的砂性土、岩土、混合土等性质的土壤，由于压缩模量较大，经计算其CF 值较小，因此不易于沉降的发生.

2.3 区域沉降整体性分析

2.3.1 影响因子敏感性指数分析

通过上述的分析可知，各个影响因子的CF 值反映了各个因子对地面沉降的影响程度，同一类因子的不同级别对沉降的影响大小也是不同的.对于某一类影响因子来讲，其不同级别确定性系数的取值范围可以从整体上近似地反映出该因子对沉降的影响程度.因此，采用敏感性指数E可以从整体上来表征某一类因子对地面沉降的影响程度，其计算方法如下

式（2）中：E为一种沉降影响因子对沉降事件发生的敏感性指数；CFmax为CF 值在各个沉降因子不同级别中的最大值；CFmin为CF 值在各个沉降因子不同级别中的最小值.由不同沉降影响因子CF 值确定的E值是CF 值的最大值与最小值之差，沉降敏感性指数E的大小，反映了每个影响因子对地面沉降产生的敏感性程度，它也是进行地面沉降敏感性分析的一个重要量度.

经过计算可知，不同影响因子对沉降的确定性系数值E的范围，可以从整体上体现出该因子对沉降产生的敏感性程度（见表5）.通过各个沉降影响因子敏感性指数E的大小及其绘制的折线图中（见图3）可以总结得出，在4 个影响因子中，渗透系数是对研究区地面沉降空间分布影响最大的因子，其次是压缩模量，然后是地下水埋深，最后是压缩层厚度，它的敏感性程度相对最低.这说明地下水开采仍然是影响研究区地面沉降的主要因素.

表5 地面沉降因子影响程度表

图3 地面沉降因子对沉降的影响程度图

2.3.2 沉降敏感性区划分析

根据住房和城乡建设部《建筑变形测量规范国家和地区的技术规范JGJ8—2007》和天津市国土资源和房屋管理局《天津市地质灾害危险性评估技术要求》等国家和地区的技术规范规定，年均沉降量大于50 mm的沉降区域被称为沉降高敏感性区域，或称危险性区域，即可能会对建筑物或市政基础设施产生危害的严重沉降区域，因此在城市的规划与建设中，若要科学合理地分析地面沉降产生的影响，减少地面沉降带来的危害，则需要对地面沉降敏感性的空间分布进行区域划分，笔者依据由确定性因子模型计算得到的地面沉降各影响因子敏感性指数，应用ArcGIS 软件的叠加分析功能，绘制出研究区地面沉降的敏感性分布图，并采用重分类工具将研究区的沉降敏感性分为5 个等级，即年均沉降量在[0，10] mm 区间为划定为低敏感性区域；在（10，20] mm 区间为划定为较低敏感性区域；在（20，30] mm 区间为划定为中敏感性区域；在（30，40]mm 区间为划定为较高敏感性区域；大于40 mm 的沉降区域被划定为高沉降敏感性区域，从而得到天津滨海新区的地面沉降敏感性区划图如图4所示.

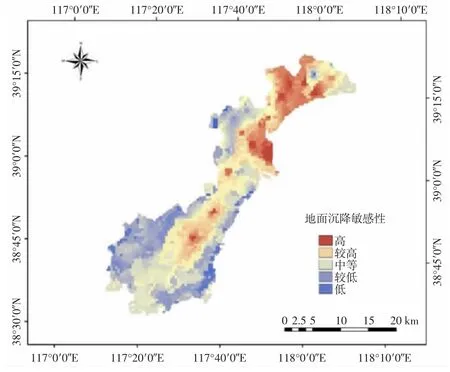
图4 地面沉降敏感性区划图

由图4，结合研究区的确定性因子模型敏感性分析结果可以看出，研究区东部地区的沉降敏感性整体高于西部，说明东部地区更容易发生沉降.图中沉降敏感性高的区域主要分布在滨海新区的东北部，沉降敏感性低的区域主要位于研究区的西南部.

再依据沉降敏感性的不同等级，计算得到每个分级区间的栅格面积大小，进而求出研究区地面沉降的敏感性区划指标及面积百分比，如表6 所示.

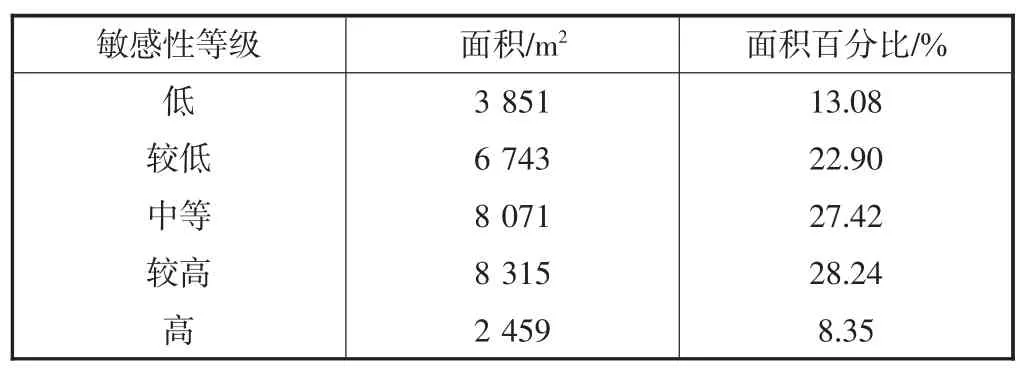
表6 地面沉降敏感性区划指标

表6 显示了不同沉降敏感性等级中沉降分布百分比的情况，其中低、较低、中等、较高、高的类别分别占研究区总面积的13.08%、22.90%、27.42%、28.24%和8.35%.中等以上占比超过了60%，这说明天津滨海新区的地面沉降现状仍然不容乐观，需要对其发展趋势进行实时监测并采取相应措施加以控制.

3 精度验证

本次研究计划通过定量统计量度来验证确定性因子模型对研究区地面沉降敏感性计算的准确程度，并据此来评价其精度的高低，量度指标主要包括卡帕系数、精度、灵敏性和特异性.

卡帕系数（Kappa）主要用于评估计算模型的可靠性，它是由观察到的（Pobs）和预期一致（Pexp）的比例计算得到，其计算公式如下

式（3）中Pobs和Pexp分别是被正确归类为沉降或非沉降的栅格百分比，以及偶然估计一致性的栅格百分比[24].通过计算最终得到模型的卡帕系数为0.903 2，这说明确定性因子模型的可靠性较强，得出的数据较为可靠；另外，模型的K 值大于0.8，说明此模型是一种较为完美的模型.

模型灵敏性（Model Sensitivity）主要表征模型中的沉降栅格被正确分类为沉降类别的概率[25].其具体计算公式如下

式（4）中，正确正误（TP）和错误正误（FP）被描述为正确和错误地分类为沉降发生的沉降栅格数，真负（TN）和假负（FN）说明正确和错误地归类为非沉降发生的栅格数. 依据统计沉降分布中出现的TP 值、FN值，来计算确定性因子模型的灵敏性，最终得到其数值为0.946 8，表示94.68%的沉降栅格被正确分为相应的沉降类别，这说明由确定性因子模型计算得到的沉降敏感性数据灵敏度较高.

模型特异性（Model Specificity）表征模型中的非沉降栅格被正确归类为非沉降类别的概率[26].其具体计算公式如下

依据统计沉降分布中出现的TN 值、FP 值，来计算确定性因子模型的特异性，最终得到其数值为0.956 5，表示95.65%的非沉降栅格被正确分为相应的非沉降类别，这说明确定性因子模型的特异性较大，计算得到的沉降敏感性数据较为特异.

模型准确性（Model Accuracy）表征模型中的栅格被正确归类为指定类别的概率[27].其具体计算公式如下

依据前面计算得到的模型灵敏性和特异性的数值来计算确定性因子模型的准确性，最终得到其数值为0.951 7，这说明确定性因子模型的计算准确性较高，得出的数据较为准确.

从以上分析可以看出，模型的各项评价精度指标都很高，说明此模型对区域地面沉降的真实值拟合较好，是一个比较理想的信息评价模型.

此外，本文通过受试者操作特性曲线（Receiver Operating Characteristic Curve，ROC）[28-29]，来对确定性因子模型的概率统计预测性能进行验证，ROC 曲线下的面积（AUC）是能够反映模型预测能力高低的一项精度指标，AUC 值越高表示预测能力越好，当AUC 值为1 时表示模型的预测性能百分之百正确. 本文应用Origin9.0 软件，绘制了模型的ROC 曲线，经计算，其AUC 值为0.851 6（见图5）.结果表明，应用此模型预测得到的研究区地面沉降敏感性区域与已知地面沉降发生区域的重合程度较高，因此此模型对研究区内的地面沉降具有精确的分析计算能力和较好的预测可信度.

图5 模型分析得到的ROC 曲线图

4 结 论

区域沉降敏感性分析和区划是进行区域沉降敏感性评估和预测的基础，本文在对天津市滨海新区地面沉降现象进行实地勘测的基础上，首先应用克里金插值方法对研究区内的钻孔数据进行空间插值，获得了渗透系数、地下水埋深、压缩层厚度、压缩模量4 个影响因子的空间分布图，然后基于确定性因子模型计算了各个因子对沉降敏感性的影响大小，最后进行了研究区的沉降敏感性区划分析，绘制得出沉降敏感性区划图，从而为该区域沉降灾害的研判和预测预警提供了科学的依据.本文的主要结论包括：

（1）通过确定性因子模型对于4 个沉降因子的计算结果可知，4 个影响因子中渗透系数因子对于沉降发生的影响最大，其次是压缩模量，然后是地下水埋深，压缩层厚度因子对沉降的影响最小；另外，同一因子中不同级别对于沉降发生的影响也不尽相同，其中，研究区内沉降发生较频繁的渗透系数范围位于[3.49，3.57]×10-6kV（cm/s）区间，地下水埋深范围位于（130，170] m 区间，压缩层厚度范围位于（80，100] m区间，压缩模量范围位于[68.49，81.20]MPa 区间，说明这些区间是地面沉降的易发区.

（2）结合研究区地面沉降敏感性的区划分析结果可以看出，滨海新区的东部地区沉降的敏感性整体高于西部，敏感性高的区域主要位于滨海新区的东北部，而敏感性低的区域主要位于滨海新区的西南部.地面沉降总体上呈现东高西低的态势，说明研究区内沿海地区的沉降敏感性高于内陆地区，更容易发生沉降，应该在这一地区采取有效的预防措施来防范沉降可能带来的危害.

（3）通过对确定性因子模型的精度检验，说明由该模型生成的沉降敏感性指数对研究区内已发生的沉降具有较好的“诊断”作用，其预测结果与实测结果也具有很好的一致性，从而证明了这种方法的有效性和实用性.

综上所述，应用确定性因子模型计算并分析地面沉降敏感性，可以准确有效地处理多因素驱动的非线性地学问题，真实反映各相关因素对地面沉降的影响，其输出结果也能够比较清晰地反映出沉降变形的分布现状和发展趋势.

需要指出的是，地面沉降是一个十分复杂的非线性区域灾害问题，其影响因素也是非常多的[30-34]，本文只是在一个相对比较小的区域内，结合比较常见的4个影响因子对地面沉降的敏感性进行了分析和探讨，如果区域环境发生改变，则应该将地下工程施工、土地利用类型、坡度坡向、地下水径流等其他因素综合考虑进来，根据不同的空间尺度效应，构建更加精准的模型，进行分析和预测.