约束条件下基于改进免疫算法的项目工期进度优化
王淑苹,冯为民,黄良辉,刘 隽
(1.广东南华工商职业学院 建筑与艺术设计学院,广东 广州 510507; 2.广东工业大学 土木与交通工程学院,广东 广州 510006; 3.广东建设职业技术学院 土木工程学院,广东 广州 510440; 4.武汉理工大学 安全科学与应急管理学院,湖北 武汉 430070)
项目工期优化作为项目科学化管理水平的重要评价指标,通过工期优化,可为项目组织方案与成本控制提供精细策略。项目的工期进度优化通过智能算法实现了项目工期、成本和项目的资源利用率的科学统筹[1]。根据不同优化角度的目标函数和项目约束条件,建立合适的优化模型,从而得到项目进度调度策略。
在项目工期进度优化中,由于项目的工艺顺序、设备资源的数量及连续工作时间限制、项目施工的自然环境和外部政策等因素,这些多重复杂的约束条件使得工期优化的难度攀升,这给工期优化建模提出了更高的挑战。当前,关于工期进度优化研究较多,谢存仁等[2]采用遗传算法用于项目工期进度优化,并借助建筑信息模型(Building information modeling,BIM)对进度进行有效分解,从而从不同角度得到完整的进度样本特征变量。试验证明,该方法在解决多目标的进度优化时,具有较强的预测性能,但其焦点主要放在多目标函数优化求解方面,而在多约束条件方面的进度寻优并没有展开;蒋淑云等[3]采用关键链技术用于项目进度优化,主要针对任务耦合程度高,工序逻辑顺序复杂的项目进度优化,能够解决复杂约束条件下的工期进度优化问题,但是其优化精度和效率均有待提高。
本文采用免疫算法队项目工期进行优化,将抗体和抗原的亲和度计算策略应用于项目进度策略和进度目标函数的匹配求解,并采用鲸群算法来快速搜寻最高亲和度个体。试验结果表明,通过该方法能够获得更优的工期进度方案。
1 多约束条件工期进度优化数学描述
在工期进度优化过程中,主要是实现在允许工期的范围内提高最小成本的期望值,假设在提高该期望值的过程中,使用的进度调整策略为λ=[λ1,λ2,…,λn],其中λi为每个时间点执行的任务名称,设工期和成本分别为T(λ)和E(λ),那么进度优化问题转化为
(1)
式中:T0表示合同工期,E表示期望求解。
下面继续对约束条件下的工期优化方法进行数学描述。
构建n个任务在m个资源情况下的工期模型,设任务i需要的资源k的数量为ri,k,Rk为资源k的总数量,设PSTi、PSTj和PPj分别为任务i开始时间,任务j开始时间和工期,P(i)表示i的前项任务,那么整个项目工期Period优化模型为
(2)
式中:Tc(t)和CT分别为t时刻正在执行的任务集和当前时间。
在式(2)中列出的直接约束条件主要是项目中任务的起始和停止时间、顺序关系以及任务的资源使用情况,而这些直接约束条件的形成受到项目运行过程中多种因素的影响,这些因素根据项目的类型不同呈现了一定差异,部分因素如表1所示[4]。

表1 项目的部分约束条件
2 基于鲸群的免疫算法工期进度优化
2.1 免疫算法
免疫算法(IA)作为防御机制的体现,通过抗体和抗原来的亲和关系来进行算法求解,其实现机制数学描述如下。
设IA算法规模为N,抗体总维度为M,则种群个体的信息熵为[5]:
(3)
(4)
式中:s表示某抗体选择的维度数。
上式中的Pij计算方法为[6]
(5)
式中:Tis表示第i个抗体在s维出现的次数。
抗体u与w两者的亲和力计算公式[7]
(6)
式中:η∈[2,N]。
当γuw=1时,表示u与w相同,u与w的相似性和γuw值正相关。
抗体u的浓度Cu为[8]
(7)
式中:T浓度阈值。
根据计算的亲和力值,判定抗体和抗原亲和度,若满足要求,则该抗体为最优解,若不满足,则进行抗体浓度计算,选择浓度值高的个体进行新抗体复制,产生新的抗体种群,执行式(2)~(5),直到找到与抗原最接近的抗体。
2.2 鲸群算法(WSA)
WSA通过鲸鱼猎食过程中的搜索、包围和攻击等方式来进行优化解的搜寻,这3种不同运动方式可以实现鲸群活动范围内极优值的发现与追寻。下面将对WSA的3种运动方式进行数学描述。
设一头鲸鱼的当前位置为X,其搜索猎物方法为[9]
D=|C·Xrand-X|
(8)
X(t+1)=Xrand-A·D
(9)
式中:| |为绝对值运算,Xrand是随机位置,A、C均为系数向量[10]
A=2a·r-a
(10)
C=2r
(11)
式中:r是[0,1]的随机向量。
对鲸群所有个体执行式(8)和(9)式完成猎物的搜索,从而实现极优值的粗粒度搜索,当发现猎物可能位置时,记录猎物的位置X*。
获得X*后,进行极优解的细粒度搜索,可以继续采用猎物搜索方法进行位置更新[11]
D=|CX*(t)-X(t)|
(12)
X(t+1)=X*(t)-A·D
(13)
获得X*后,也可以采用螺旋攻击方法进行位置更新[12]
X(t+1)=D·ebl·cos(2πl)+X*(t)
(14)
式中:b为常量,l为rand(-1,1)。
在获得X*后,两种位置更新的方法选择由概率p决定。
(15)
迭代更新X(t+1),不断更新猎物位置X*,寻找最优鲸群个体[13]。
2.3 WSA-IA算法的进度优化流程
在获得项目数据样本后,需要对样本特征进行编码及向量化,根据项目工艺顺序、设备使用时间及顺序等约束条件,结合式(2)生成目标函数。接着,以目标函数为抗原,建立免疫算法的进度优化模型,计算所有种群中的抗体适应的,通过鲸群算法找出以抗原亲和度最高的个体,即为进度优化方案,具体流程如图1所示。
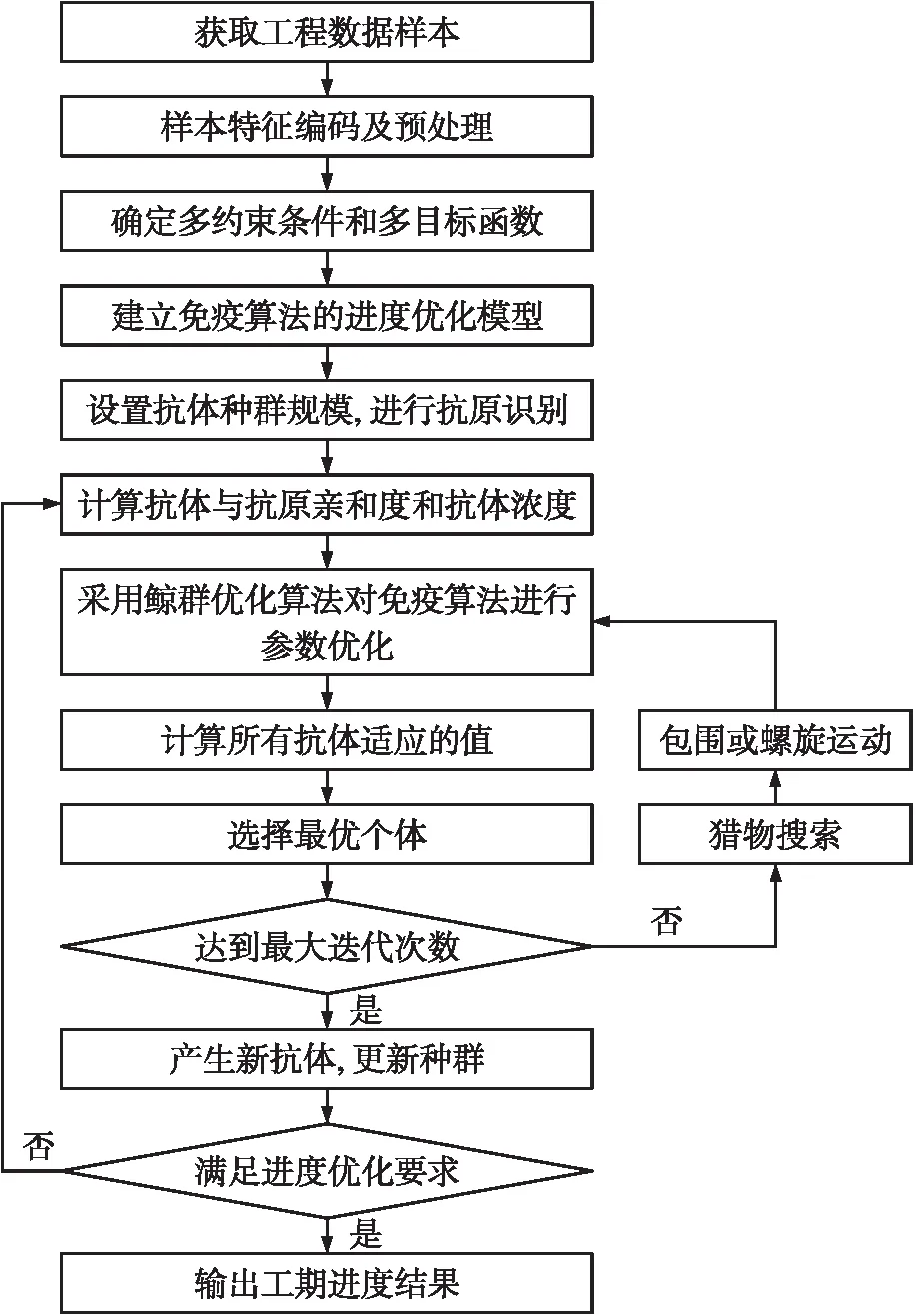
图1 基于WSA-IA的进度优化流程
3 实例仿真
为了测试WSA-IA算法的工期进度优化性能,对某国有建筑集团在2021年度承接的6个不同类型建设项目进行实例仿真,数据集如表2所示。首先,采用不同的约束条件进行WSA-IA的工期进度优化求解,判断不同约束条件下得到的优化结果;其次分别采用IA算法和WSA-IA算法进行进度优化仿真,验证WSA对IA进行优化的提升程度;最后对6个项目进行4种进度优化算法的性能对比。
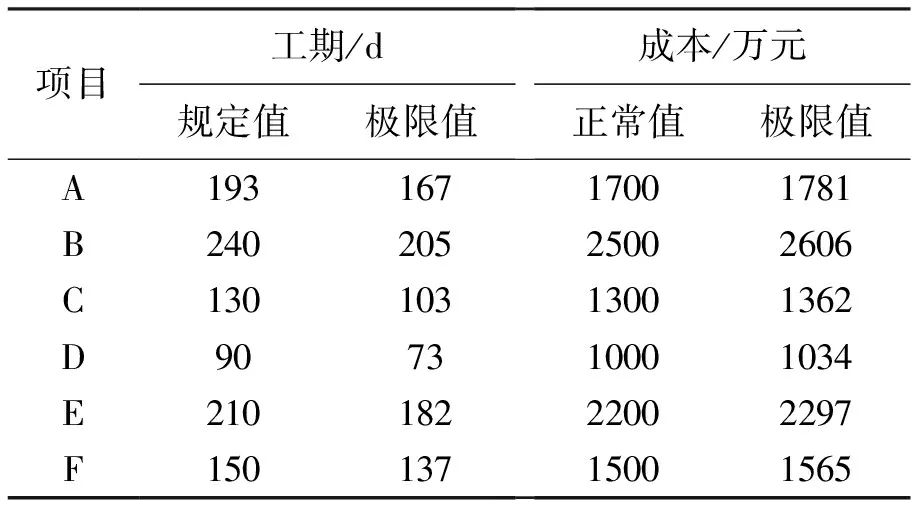
表2 仿真样本
关于6个项目内部任务的各工艺顺序、任务起止时间、设备使用顺序及时长控制等约束条件均从样本中获得。
3.1 基于WSA-IA的进度优化
以工期极限值为约束条件,进行WSA-IA算法的工期优化,找到最短工期值;然后以成本极限值为约束条件,进行WSA-IA算法的工期优化,找到最低成本值,最后以工期规定值和成本极限值进行优化,计算优化结果。

表3 WSA-IA的优化结果
从表3知,对于同种样本,采用的约束条件不同,WSA-IA的优化结果差异明显。对于项目A,在不计成本时,WSA-IA获得的最短工期为168天,但成本超出了极限值51万元,而只从节省成本角度来看,获得的最低成本为1 697万元,但工期超出规定值28天,而加上工期规定值和极限成本等约束时,WSA-IA获得的工期和成本分别为176天和1 742万元,均在工期规定值和成本极限值范围内。对于其他5个项目,在只选择一项约束条件时,即使其优化得到的工期或成本具有优势,但是却不能用于实际进度优化策略,因为出现了工期或成本超出规定范围的情况。
3.2 IA的改进性能
为了验证工期优化应用中WSA算法对IA算法的改进程度,分别采用IA算法和WSA-IA算法对工期进行优化仿真,求解工期和成本最优个体。仿真的约束条件其工期和成本均在规定值和极限值范围内。
从图2得,IA算法和WSA-IA算法优化得到的工期均在规定值范围内,没有出现工期逾期的问题,但对比发现,WSA-IA算法求解的工期比IA求解的工期短,IA求解的工期更靠近规定值,横向对比,项目F上,2种算法求解的工期值和规定值均很接近,这说明项目F的可优化程度较低;而项目A、B和D,WSA-IA求解的工期和规定值相差较远,说明这3个项目的工期可优化程度高。

图2 IA和WSA-IA算法的工期
从图3得,IA和WSA-IA算法求解的最优个体所对应的项目成本有一定差异,其中2种算法在项目A、D和F中求解的成本与正常成本非常接近,而在项目B、C和E中,WSA-IA算法所得成本明显低于IA算法所得成本。

图3 IA和WSA-IA算法的成本
综合得,采用WSA对IA进行优化后,针对6个项目求解的工期进度最优个体,其对应的工期和成本均得到了不同程度的优化,这说明在IA的工期进度优化中,WSA的优化性能得到试验验证。
3.3 不同算法的进度优化
分别采用混沌果蝇[14]、PSO-SVR[15]、混合遗传[16]及WSA-IA算法对6个项目进行工期进度优化。在相同的工期、成本约束条件下6个项目所需运算时间如表3~8所示。

表3 项目A的优化解

表4 项目B的最优解

表5 项目C的最优解

表6 项目D的最优解

表7 项目E的最优解
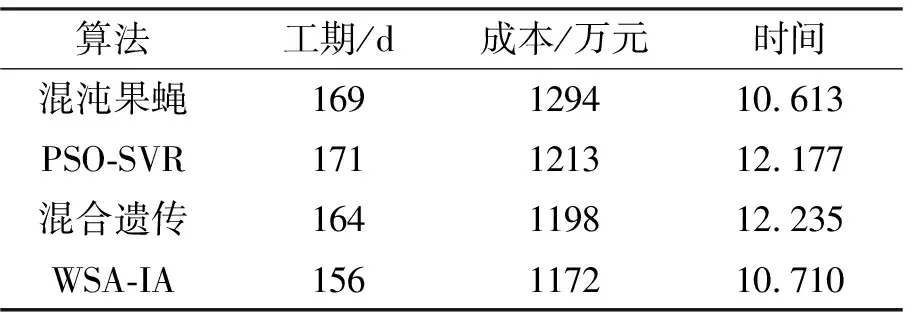
表8 项目F的最优解
从表3~8知,对于同种项目,在工期规定值和成本极限值的双重约束下,4种算法所得到的优化效率差距较大。对于项目A,在优化时间方面,混沌果蝇和WSA-IA算法耗时较少,两者所用时间非常接近,而PSO-SVR和混合遗传更耗时,在其他5个项目的优化中,WSA-IA算法仍展现出了巨大优势。横向对比,4种算法的优化效率与工期长短和成本高低没有绝对的联系,4种算法在项目C的优化效率普遍较高,而在项目F的优化效率均较低。这可能是由于不同项目本身建设的工序步骤和设备数量差异造成的,导致优化求解建模型复杂度攀升。
综合对比,虽然WSA-IA算法在优化效率方面随略低于混沌果蝇算法,但是在进度和成本最优解方面相比其他3种算法有绝对优势,其对不同类型建设项目的工期进度适应力均较强。
4 结束语
在工期和成本的双重约束条件下,采用鲸群算法对免疫算法进行改进后,免疫算法在项目工期进度优化求解中获得了更优质的解。后续研究将进一步微调鲸群算法参数,以进一步提高鲸群算法对最优抗体的寻找精度和效率,同时设置更多、更细粒度的约束条件来测试WSA-IA在工期进度优化应用中的适应度,验证WSA-IA算法在不同规模约束条件下的工期进度优化性能。

