基于多观测隐非齐次HMM的光伏功率概率预测

马 琼，马 雷，汪佐浩，张 浩

(1.国网临夏供电公司，甘肃临夏 731100；2.西安理工大学水利水电学院，陕西西安 710048)

光伏发电系统因其分布灵活、可靠性高的特点在推动电源结构清洁化进程中拥有较强的竞争力，是实现我国“碳达峰、碳中和”战略目标及推动构建以新能源为主体的新型电力系统的重要支撑技术之一[1-2]。然而，光伏输出功率较强的随机性、间歇性与非平稳特性给光伏发电系统进一步的集成应用带来巨大挑战[3-5]。稳定可靠的预测技术对于电网适应高比例新能源接入与构建健全的电力系统风险防控机制具有重要意义。

传统光伏功率预测的研究大都致力于建立输出更接近预测对象真实测量值的确定性预测模型，即输出预测对象未来某时刻的单点期望值[6]。然而，确定性预测结果缺乏对光伏发电功率不确定性信息的描述，使得能源系统设计规划、电网调度、电力市场等场景决策者难以在实际工程实践中做出最优决策。因此，需要更为全面的预测信息以在最大程度上提高实践中应对光伏出力不确定性的能力。在这种情况下，概率预测理论开始逐渐得到关注。

概率预测是应对光伏出力高度不确定及可变性的一种解决方案，通过量化随机过程不确定性，以概率密度、分位数、预测区间或综合形式发布预测结果，提供待预测对象完整的概率统计信息。近年来，越来越多的光伏发电应用场景将能源不确定性纳入决策制定的考虑范围，如分布式能源系统设计规划、能源管理系统(energy management system,EMS)优化调度、电力市场交易等，这就需要稳定、可靠、准确的功率概率分布信息提供数据支撑。概率预测在提高可再生能源占比、能源利用率及能源系统弹性性能中发挥重要作用。

概率预测方法按照采用模型的不同可分为物理方法、统计学方法、人工智能方法、组合方法等。刘洁等基于高阶马尔可夫链和高斯混合模型进行建模，计算得到光伏出力概率密度函数[8]。王开艳等基于气象特征数据，采用模糊C 均值聚类方法进行相似日划分，利用分位数回归及卷积神经网络(CNN)与双向长短记忆神经网络算法(BiLSTM)建立了QRCNN-BiLSTM 光伏功率短期概率预测模型[9]。尽管这些方法都取得了一定程度的效果，然而他们要么过于复杂难以在实践中应用，要么基于一些在实际应用中难以验证的假设。

隐马尔可夫模型(hidden Markov model,HMM)基于少量非限制性假设，描述双随机过程非线性动力学特性，被广泛应用于故障诊断、信号识别、气象预测等领域[10]。由于光伏发电过程与气象变化过程均为随机过程，理论上只要确定状态空间与观测空间，便可使用HMM 很好地描述两者的关系。同时，非齐次HMM 允许隐藏状态受到相关协变量的作用，考虑了时间尺度的影响，能更好地描述研究对象与复杂作用因素关系。

鉴于此，本文提出基于多观测非齐次HMM 的光伏出力概率预测模型。首先，介绍了传统HMM 的基础原理及多观测非齐次HMM 的推导与基础问题的求解。接着，引入百分比离散参数建立光伏出力及相关气象参数离散有限集合，即建模所需的状态空间与观测空间。基于真实光伏电站运行数据建立出力概率预测模型，输出未来各时刻点光伏出力概率分布信息。最后，通过与传统HMM、单/多观测非齐次HMM 模型、支持向量机模型(support vector machine,SVM)的比较对所提出模型的可行性与预测性能进行了分析验证。

1 模型的构建

1.1 隐马尔可夫模型

图1 展示了隐马尔可夫过程示意图，st－1，st，st+1分别表示在t－1、t、t+1 连续时刻下状态值，相对应的ot－1，ot，ot+1分别为各时刻下的观测值。

图1 隐马尔可夫过程

状态值与观测值分别属于对应的状态空间与观测空间。使用Q与V分别表示HMM 的状态空间与观测空间：

式中：N与M分别为可能存在的状态与观测数量。

隐马尔可夫模型可以表示为：

式中：A与B分别表示状态转移概率矩阵与观测概率矩阵；π为初始状态概率向量。

式中：aij为从t时刻状态为qi转移到t+1 时刻状态为qj的概率；bi(k)为t时刻在状态为qi情况下产生观测值vk的概率；πi为初始处在状态qi的概率。

1.2 多观测非齐次隐马尔可夫模型

传统的隐马尔可夫模型有两个基本假设：

(1)齐次马尔可夫性质。对于状态序列而言，任意时刻状态只与前一个状态有关，与其他时刻的状态和观察无关。

(2)观测独立假设。对于观测序列而言，任意时刻观察只取决于同一时刻状态值，而与其他时刻观察与状态无关。

如图2 所示，本文将传统HMM 扩展为拥有σ 阶记忆马尔可夫链的非齐次HMM，即未来状态的条件概率分布取决于过去的σ个状态，同时引入多观察序列，记为σ-MOHMM。

图2 σ阶多观测隐马尔可夫模型(σ-MOHMM)

1.3 模型求解

本文采用最大似然估计(maximum likelihood estimate,MLE)、前向后向算法及近似算法来解决光伏概率预测模型建立过程中的学习问题与预测问题。对于HMM，使用MLE 方法得到其转移概率与观测概率，可以表示为：

式中：nij为数据集中由状态qi向状态qj转移的个数；nik为在状态qi下观测为vk的个数。

对于有N个状态M个观测的HMM，状态转移概率组成N×N矩阵，观测概率组成N×M矩阵，矩阵的每一行元素的总和为1，如图3 所示。

图3 概率矩阵

σ-MOHMM 的转移概率与观测概率矩阵：

高阶HMM 概率矩阵的维度随之增加，图4 展示了二阶状态转移概率矩阵，为N×N×N的矩阵。

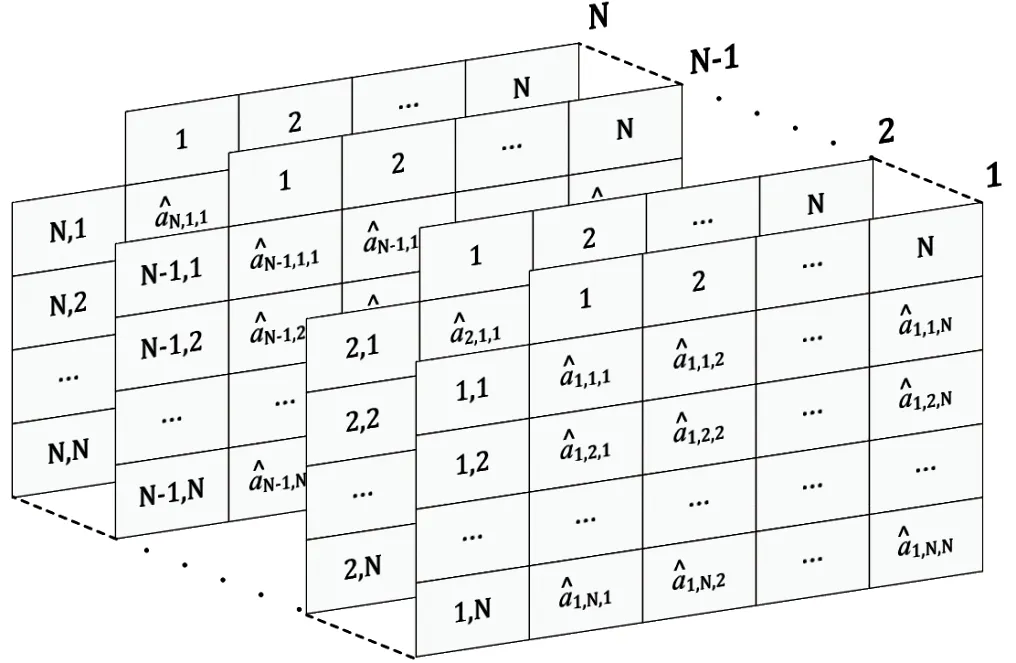
图4 二阶状态转移概率矩阵

预测问题是指在给定模型λ 及一定时间段的观测序列O(d)，计算最有可能出现的状态序列。对于σ-MOHMM，其前向后向概率可以由以下步骤计算：

(1)计算初值：

式中：α与β分别表示前向概率与后向概率。

(2)迭代计算：

(3)最终，t时刻处于状态qj的概率可以表示为：

1.4 光伏概率预测模型构建

光伏电站的额定功率决定了其最大出力的理论值。用Pn表示光伏电站额定功率，则状态空间区间可以表示为[0,Pn]。同理，用Rn表示理论最大观测值，则观测空间区间可以表示为[0,Rn]。参数离散化后得到的状态空间与观测空间的可以表示为：

式中：θ为百分比参数，θ×Pn与θ×Rn分别为状态空间与观测空间的数据间隔。

2 模型输出与评价指标

2.1 模型输出

本文采用以下两种方式计算确定性预测结果：

(1)均值

(2)众数

置信度1－μ下预测区间可以表示为：

2.2 模型评价指标

采用归一化均方根误差(NRMSE)作为确定性预测评价指标，计算方式如下：

式中：T为观测序列长度，即待预测点个数；st为t时刻实测状态值；为t时刻预测状态值；Pn为光伏电站额定出力。

概率预测区间一般从可靠性、锐度两个方面进行评价。可靠性指标用来描述预测分布与预测对象实际分布的接近程度。采用预测区间覆盖率PICP来描述预测区间的可靠性，PICP越接近实际置信度(1－μ)%则代表预测结果有更好的可靠性，计算方式如下：

锐度指标用于衡量概率预测结果集中于实际值的程度。采用Winkler 分数(SW)描述模型锐度性能，SW越小则预测结果有更好的锐度性能与综合性能，计算方式如下：

3 实例分析

本文基于国内某光伏电站时间跨度为2 年的光伏出力及气象参数数据，电站额定出力20 MW，最大短波辐射810 W/m2，最小潜热通量－450 W/m2，数据步长为15 min，有效数据698 d。表1 展示了光伏出力与各气象参数皮尔逊相关性系数关系，选取与光伏出力具有较强相关性的总辐照度与潜热通量作为观测变量。由此得到状态空间与两个观测空间区间分别为状态空间A=[0,20]，观测空间B1=[0,810]与B2=[－420,0]，离散参数θ为1%。

表1 光伏出力与气象参数皮尔逊相关性系数表

3.1 模型参数估计

图5 展示了传统HMM 模型的状态转移概率矩阵直方图。可以看出，转移概率分布在矩阵的对角线上，同时由两侧对角线向内逐渐衰减，表明出力数据步长满足连续时间物理过程的近似表示。图6 展示了观测概率矩阵直方图，相较于状态转移概率矩阵更为分散。这意味着同一气象参数值对应多个光伏出力，从侧面印证了光伏发电是一个受到多因素共同作用的复杂随机过程。

图5 状态转移概率矩阵图

图6 观测概率矩阵图

3.2 预测结果输出

基于待预测时间段的气象预测序列，通过计算前向后向算法得到各时刻点对应出力概率分布。如图7 所示，结果概率分布是一个T×N矩阵，即每个时刻下对应N个状态的概率分布。基于此，可以得到各时刻点确定性预测结果及不同置信度下预测区间，如图8 所示。

图7 预测结果概率分布图

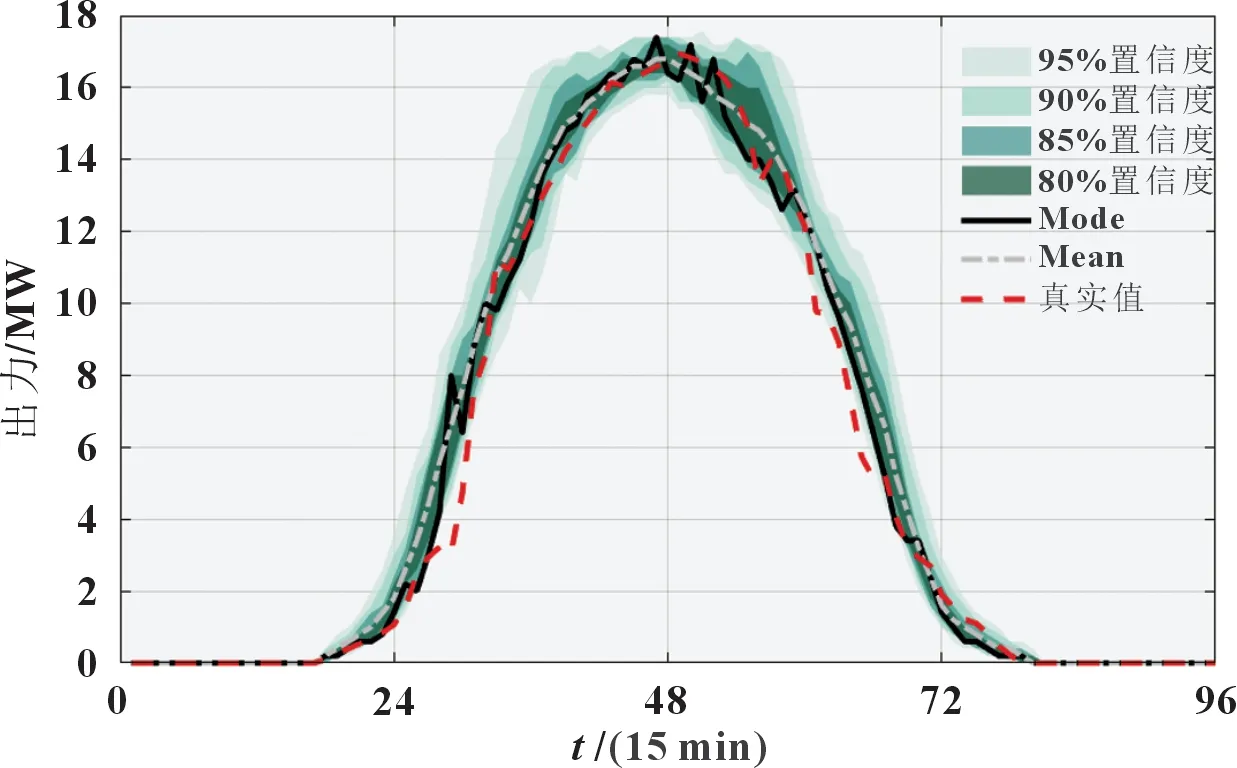
图8 光伏出力概率预测与确定性预测结果

3.3 模型分析评价

本节将对传统HMM、2-HMM 以及2-MOHMM 三个概率预测模型的概率预测性能，以及与SVM 模型确定性预测性能进行对比分析。其中，SVM 模型选取径向基核函数，正则化参数为200，核参数为10。按照以下步骤对上述各个模型进行交叉实验：(1)随机选取三天数据作为测试集，其余数据用于模型训练。(2)训练好的模型输出90%置信度预测区间与确定性预测，同时记录保存模型评价指标计算结果。(3)重复(1)(2)步骤，直至达到设定阈值。(4)对指标进行统计分析，得到预测性能指标分布。

通过测试发现，当阈值达到1 000 次之后，各模型预测性能指标分布趋于稳定，因此选择测试迭代次数1 000。图9 与图10 分别展示了概率预测性能统计结果与确定性预测性能统计结果，以概率密度直方图形式进行展示，阴影部分为概率分布的核密度估计。

图9 光伏出力概率预测性能指标统计图

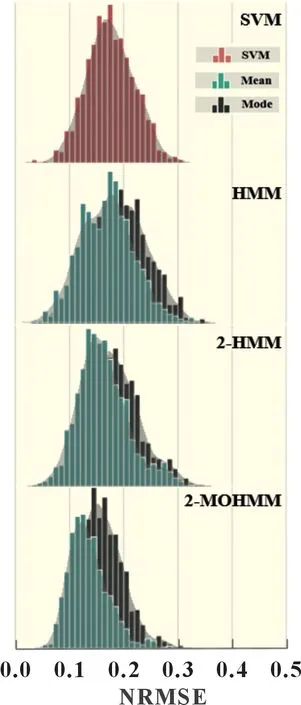
图10 光伏出力确定性预测性能指标统计图

由图9 可以看出，概率预测性能随着马尔可夫链阶数的提升有明显的提高，具体表现为可靠性指标PICP 分布明显右移，更接近实际置信度，拥有更好可靠性。同时，区间分数SW随着阶数δ的提升逐渐减小，说明概率预测模型锐度及综合性能的提升。另一方面，多观测变量的引入对概率预测模型的可靠性与锐度性能有促进作用。

对于确定性预测结果的输出而言，均值法相较于众数法拥有更准确的点预测输出，指标分布偏向于更小的NRMSE。与概率预测性能类似，阶数的提升及双观测变量对模型的确定性预测性能有明显提升。传统HMM 模型确定性预测性能与SVM 模型接近，扩展后的2-HMM 与2-MOHMM 均明显优于SVM。

4 结论

本文将隐马尔可夫模型扩展并应用于短期光伏发电功率预测，包括不同置信水平的概率预测区间及通过统计方法得到确定性预测结果。首先通过确定相关参数边界及对其离散化处理获得状态空间和观测空间，接着基于真实运行数据建立HMM 概率预测模型，输出未来时刻点光伏功率概率分布信息。基于真实光伏电站两年共计698 d 运行数据对传统HMM、单观测二阶HMM、双观测二阶HMM 以及支持向量机SVM 四种模型进行了交叉模拟预测实验。通过统计分析比较各个模型预测性能指标证实了基于HMM 的光伏概率预测模型的可行性与有效性。同时，考虑历史状态和观测对当前观测和状态的影响对HMM 模型确定性预测及区间预测性能都有明显提升。