抗传感器噪声的锂离子电池SOC估计方法

孔令昊，杜常清，任 重

(武汉理工大学汽车工程学院，湖北武汉 430070)

电池管理系统(battery management system,BMS)是新能源汽车动力系统中不可缺少的部分，其对于锂离子动力电池状态的估计功能是保证电池安全高效使用的基础。荷电状态(state of charge,SOC)是评价电池剩余电量的指标，是方便用户使用车辆与进行充电规划的依据，直接影响着消费者的用车体验，是车载BMS 的基础核心内容。

随着技术的发展，锂电池SOC的估计方法逐渐成熟。目前针对车载动力电池SOC的估计方法有安时积分法、系统滤波法与数据驱动法[1]三大类。安时积分法在目前的新能源汽车上被广泛使用，而由于采样精度与频率的限制，在实际的运行过程中会产生累积误差导致SOC估计精度下降。文献[2]基于电池电化学机理，通过对积分环节中的参数进行修正，有效减小了累积误差的影响，提高了算法的估计精度，但是方法对不同品牌型号的电池仍然无法适应。系统滤波法由于其对于非线性系统的良好预测能力而逐渐成为了SOC估计研究的主流方法。文献[3]使用基于卡尔曼滤波的非线性衍生算法与粒子滤波法取得了良好的SOC估计精度。近年来，随着机器学习与大数据的快速发展，前馈神经网络[4-5]、支持向量机[6]、循环神经网络[7]等基于数据驱动的估计方法也被大量研究，并取得了较好的SOC估计效果。

在实际应用中，传感器的精度与成本一般相互矛盾，作为成熟的商品，汽车成本控制是必不可少的。较为精确的电池模型电压估计误差在±20 mV 上下[8-9]，而目前车载BMS 常用的电压传感器噪声最大可达10 mV，再叠加电流传感器的噪声，无疑会造成额外的估计误差。

为了更好地了解并降低传感器噪声对SOC估计带来的影响，提高BMS 估计算法的实用性，本文将模拟传感器噪声注入到神经网络的训练数据中，从而提高所训练的神经网络SOC估计器对传感器噪声的适应性。选取应用最广泛的BP神经网络作为研究对象，首先使用无噪声的数据集对其进行训练，再根据车载BMS 传感器的采集精度，设置了4 组具有不同噪声的测试集，研究噪声对BP 神经网络估计效果的影响。此后使用一种数据拓展的方法，将电压、电流噪声进行组合并分别注入训练集，得到原数据集9 倍大小的拓展训练集对同一神经网络进行训练与测试，并在高斯噪声工况下与拓展卡尔曼滤波(extended Kalman filter,EKF)算法进行对比。结果显示，使用拓展后的训练集能有效改善传感器噪声对BP神经网络估计效果的影响，且相比EKF 算法具有更好的估计效果。

1 数据来源

本文采用McMaster University 的电池研究小组于2020 年公布的一系列用于神经网络训练与验证的电池测试数据[10]。该研究小组使用德国Digatron 公司的实验设备对3 Ah 的全新LG 18650HG2 型镍钴锰酸锂电芯在多种温度条件下(40,25,10,0,－10,－20 ℃)进行了自定义的混合脉冲功率试验(HPPC)与多种标准驾驶循环(UDDS,LA92,HWFET,US06)的测试，设备的具体参数如表1 所示。

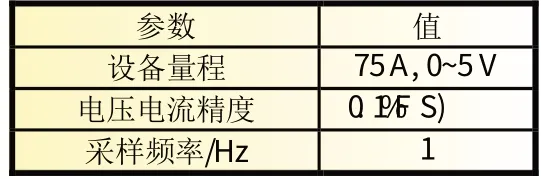
表1 实验设备参数

选取25 ℃下的HPPC 测试数据作为神经网络的训练集，UDDS 工况作为测试集。HPPC 测试中，电池在每个SOC状态下(100%,95%,90%,80%,70%,...,20%,15%,10%,5%,2.5%,0%)进行了四组脉冲放电(1C,2C,4C,6C)与四组脉冲充电(0.5C,1C,1.5C,2C)测试，SOC划分细致，电流设置范围较大，可以很好地反应各个SOC状态下电池对于不同电流激励的响应特性。每个SOC状态下的HPPC 电流加载状况如图1 所示。考虑到LA92 用于重型车辆代表性较差，UDDS工况的启停、加减速相对HWFET 和US06 工况更加频繁，故选取UDDS 工况的测试数据作为测试集。

图1 一次HPPC测试的电流加载状况

2 研究方案

本文使用包含两个隐藏层的BP 神经网络进行研究，输入为电池的电压与电流，输出为SOC，具体参数如表2 所示。

表2 BP神经网络参数

2.1 测试集噪声注入方法

为了更好地模拟实际应用场景，选取某车规级BMS 电压传感器与电流采集模块，与数据处理相关的量程、精度参数如表3 所示。将两种传感器的噪声分别视为幅值为10 mV 和150 mA 的高斯噪声，其分布情况如图2 所示。

图2 传感器噪声分布

表3 某常见型号传感器参数

在仿真工况方面，设置了电流、电压传感器误差均为最大值的最大噪声工况和高斯噪声工况。除此之外，为了更好地体现出不同类型传感器噪声带来的影响，设置了仅加入电流传感器最大误差以及仅加入电压传感器最大误差的两种工况。将噪声加入选出的测试集中，并使用训练完成的BP神经网络进行估计。

2.2 训练集数据拓展方法

为了减少传感器噪声对估计结果的影响，本文使用了一种数据拓展的方法，通过将电压、电流噪声进行组合创建了9种不同的工况，将原本的训练集扩大到原本数据量的9 倍，从而提高BP 神经网络估计器的鲁棒性。在创建训练集时，取电压噪声10 mV 与电流噪声150 mA 进行组合，得到的9 种工况如表4 所示。使用拓展后的训练集再对具有相同结构与神经元数量的BP 神经网络进行训练，并使用上文中提到的4 种注入噪声的测试工况对估计器的效果进行评价。

表4 训练集噪声组合情况

3 结果分析

本文通过控制变量的方式逐步研究传感器噪声对使用神经网络进行SOC估计的影响以及通过拓展训练集对噪声影响的优化效果，并将SOC估计效果与使用一阶RC 等效电路模型的EKF 算法进行对比，研究流程如图3 所示。

图3 本文的研究流程

3.1 无噪声状况下的估计效果

使用原始数据对BP 神经网络进行训练与测试，作为无噪声对照组为后续的研究提供参考。无噪声状况下仿真与实际SOC的对比如图4所示。无噪声状况下的估计器的最大误差、平均绝对值误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)分别为3.619 0、0.588 6和0.828 0。

图4 无噪声状况下仿真与实际SOC对比

整个过程中MAE为0.588 6%，说明BP 神经网络估计器的整体估计精度较高，虽然在电流迅速增大时SOC估计误差会突然增大，但随着加载过程的进行，误差也快速回落到较小范围，因此认为该估计器能够较好地进行SOC预测。

3.2 噪声影响下的估计效果

使用注入噪声的测试集对使用无噪声训练集训练的BP神经网络进行测试，以研究传感器噪声带来的影响。为了更加清晰地表现噪声对于估计效果的影响，选取SOC估计误差的差值作为绘图数据源。加入噪声后的SOC估计误差与无噪声对照组估计误差的差值如图5 所示。各工况下的误差对比如图6 所示。噪声干扰下SOC估计效果如表5 所示。

图5 加入噪声后的SOC估计误差与对照组的差值

图6 不同噪声工况的误差对比

表5 噪声干扰下的SOC 估计效果

从结果中可以看出：在最大噪声工况下，整个过程的MAE较无噪声工况增大了0.368 9%，增大幅度为62.7%；在加入高斯噪声的工况下，MAE增大了0.271 9%，增大幅度为46.2%；RMSE均有所增大，说明传感器的噪声对于估计器的整体精度有较大的影响，也会导致估计的稳定性有所降低。通过对比仅加入电流噪声与仅加入电压噪声的两种测试工况的结果，仅加入电流噪声与仅加入电压噪声的工况下MAE分别增大0.119 3%与0.624 9%，增大幅度分别为20.3%与106.2%。可以看出电压传感器的误差对于整体估计效果影响更明显，这主要是因为SOC与电压存在直接对应关系，估计结果对于电压更敏感。

3.3 训练集拓展后的估计效果

使用拓展训练集对网络进行重新训练后，再次使用注入噪声的4 种测试集进行测试，并在高斯噪声工况下与使用一阶RC 等效电路模型的EKF 算法进行对比。数据拓展后网络的估计误差与无噪声对照组估计误差的差值如图7 所示，各工况与算法的误差对比如图8 所示。与EKF 算法的SOC估计效果和误差对比分别如图9 和图10 所示。训练集拓展后对于测试集的估计效果如表6 所示。

图7 训练集拓展后对于测试集的估计误差与对照组的差值

图8 不同噪声工况与算法的误差对比

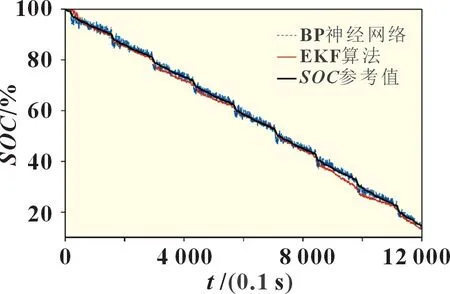
图9 高斯噪声工况下BP神经网络与EKF算法的SOC估计效果对比

图10 高斯噪声工况下BP神经网络与EKF算法的误差对比

表6 训练集拓展后的SOC 估计效果

仿真结果显示，使用数据拓展的方法对训练集进行处理后，估计器在各个工况下的精度均有所提升。最大噪声工况下MAE降低了0.196 7%，精度提高33.4%。在高斯噪声工况下MAE降低了0.203 5%，精度提高34.6%，相比EKF 算法的MAE降低0.366 8%，精度提高35.8%。两种单一噪声工况下的精度也有所提高，由于SOC对于电压有更高的敏感性，数据拓展对于电压噪声工况的精度提升更大，整个过程的MAE降低了0.386 3%，精度提高幅度达65.6%，电流噪声工况的两个数据则分别为0.073 4%与12.5%，各个工况下的RMSE均有所下降。综合以上数据与分析，在噪声影响下，通过数据拓展的方法对训练集进行处理后，相同结构与神经元数量的BP 神经网络对于锂电池SOC的估计精度更高且在估计过程中波动更小，说明这种数据拓展的方法能够较好地减小噪声带来的影响，且在整个估计过程中比EKF 算法具有更好的稳定性。

4 结论

在锂电池SOC估计算法的实际应用中，传感器噪声对估计过程的影响是无法忽略的。为了更好地了解并降低这种影响，本文通过对测试集注入噪声的方式，分别讨论了不同类型的噪声对于BP 神经网络估计器的影响，并使用一种将电压、电流噪声进行组合创建的拓展训练集对网络进行重新训练，有效降低了噪声对SOC估计的影响。具体结果为：

(1)在对测试集注入噪声后，BP 神经网络估计器的MAE与RMSE相比无噪声状况均有所增大。最大噪声工况、高斯噪声工况的MAE分别增大0.368 9%与0.271 9%，增大幅度分别为62.7%与46.2%。说明传感器噪声会对SOC的估计精度产生较大影响。对比仅加入电流噪声与仅加入电压噪声的两种工况，可以了解到SOC估计误差对于电压噪声更加敏感。

(2)通过拓展训练集的方法对具有相同结构与神经元数量的BP 神经网络估计器进行重新训练后，在含有同样噪声的测试环境下MAE与RMSE均有所下降，最大噪声、仅电流噪声、仅电压噪声与高斯噪声的MAE分别下降0.196 7%，0.073 4%，0.386 3%与0.203 5%，精度的提高幅度分布为33.4%，12.5%，65.6%与34.6%，且与EKF 算法的MAE相比降低了0.366 8%，精度提高了35.8%。