基于有限元分析的大型水轮机轴联销钉拔销强度及寿命预测方法

钱 祥，何亚文，张宝庆，李友才，吴秩嵩，周海林，黄俊玮，刘桂英

（1.湖南五凌电力工程有限公司，湖南 长沙 410004；2.长沙理工大学电气与信息工程学院，湖南 长沙 410114）

0 引言

销钉拔销系统是大型水轮机轴联检修中拆解联轴的必要设备，它的状态对大型水轮机的安全检修起着举足轻重的作用[1，2]。疲劳失效是机械元件失效中的一种主要形式，销钉拔销系统断裂主要发生在高应力区域[3，4]。为了提高大型水轮机检修拔出销钉的安全性，降低机械元件的运维成本，减少检修事故的发生次数，对于销钉拔销系统强度疲劳程度及寿命的准确预测就具备了至关重要的工程意义[5]。

已有大量学者对于销钉损伤程度及寿命预测进行了研究，姜丰 等[6]通过计算不同负荷条件下剩余寿命的分布情况，建立了载荷数-疲劳寿命的干涉模型。刘俭辉 等[7]采用剩余强度作为控制参数的传统应力强度干涉模型来对机械元件的疲劳可靠性进行分析。余天堂 等[8]提出了一种含有位置参数的对数正态分布来进行销钉剩余寿命预测的方法，同时分析了在恒幅值载荷和变幅值载荷作用下销钉的剩余寿命分布形式。杨嘉顺[9]提出了一种在复杂应力状态下仍能适用的剩余寿命预测模型，该模型是基于临界平面法搭建的。现有的研究中，对于疲劳寿命的描述主要采用正态分布以及对数正态分布的方式[10，11]。在工程应用可靠性分析中，该分布在产品寿命以及可靠性分析预测中应用广泛[12]。但是，专门针对销钉拔销系统的研究文献极少。

有鉴于此，本文针对销钉拔销系统的强度和寿命预测问题进行研究，基本思想是：根据有限元理论构建起销钉拔销系统的有限元模型，在有限元模型基础上，根据各有限单元的应力和应变分布特征，运用Smith-Watson-Topper（SWT）模型理论，建立起包含销钉拔销系统的材料属性及其疲劳参数、损伤参数的销钉疲劳强度与剩余寿命的SWT预测模型。在销钉拔销系统有限元模型中，简化了非线性预测问题，将其转化为线性预测问题，以提高基于有限元模型的强度与寿命预测模型的求解速度。

1 销钉拔销的有限元模型

有限元分析（Finite Element Analysis，FEA）是一种利用数学近似对真实物理系统进行模拟的方法。基本思想是用较简单的问题代替复杂问题后再求解，利用简单而又相互作用的有限微小单元及其有限数量的未知量去逼近无限未知量的真实系统，将整体系统的求解域看成是由许多称为有限元的小的互连子域组成，对每一单元假定一个合适的近似解，然后推导求解这个域总的满足条件（如结构的平衡条件），从而得到整体系统的解[13]。

销钉拔销系统的有限元建模原理如下：

（1）建立单元位移模式模型

将销钉拔销系统中的销钉划分为有限数量的N个微小单元u，微小单元u为刚性六面体，每个单元有8个节点，每个节点有6个自由度的位移，其中3个距离位移，3个相位位移。因此，第n（n=1,2,…,N。下同）单元un的第i节点的未知量包括6个应力变量、6个应变变量、3个位移变量，分别构成应力向量、应变向量、位移向量。位移未知量也称基本未知量。第n单元un的第i节点的应力向量可以表示为

第n单元un的第i节点的应变向量可以表示为

第n单元un的第i节点的位移向量可以表示为

第n单元的全部节点的位移向量构成的节点位移扩展向量可以表示为

将微小单元u看成一个质点，则第n单元un有6个应力变量、6个应变变量、3个位移变量，因此，第n单元un的应力向量可以表示为

第n单元un的应变向量可以表示为

第n单元un的位移模式θun表示为

设第n单元的位移模式使用线性差值表示，则θnj可以表示为

写成矩阵形式，有

对于任意单元n的任意节点i的位移变量λnij应满足：

写成矩阵形式，有

其中，xni、yni、zni为位移向量λni在xyz坐标系中的x、y、z轴上的坐标。

根据式（7）~（11），可以得到

其中，

称为形态函数（形函数）矩阵。

（2）建立单元应力向量与应变向量关系模型

第n单元un的单元应力向量δun与应变向量关系εun可以写成

式（13）中的矩阵D为

其中，E为杨氏弹性模量，μ为柏松比。

（3）建立单元应变向量与位移向量关系模型

第n单元un的单元应变向量与节点位移扩展向量关系可以写成

式（15）中，B=[Bn1Bn2… Bn8]，其中，

（4）建立单元刚度矩阵模型与载荷向量模型

根据式（13）、（15），可以得到单元应力向量δun与节点位移扩展向量的关系为

其中，S为应力矩阵，S=DB。

基于虚功原理，可得到单元的节点力扩展向量（即为单元载荷向量）与节点位移扩展向量的关系为

其中，Fn也称为节点力扩展向量，

式（17）也称单元特性方程；Kn称为单元刚度矩阵，Kn=∫VnBTDBdV=BTDBVn。Vn表示单元的体积。

（5）建立整体的总刚度矩阵模型与总载荷向量模型

整体结构的总刚度矩阵的总载荷向量分别是单元刚度矩阵和单元节点力扩展向量的叠加，因此有

如果单元载荷比较复杂，按如下表达式求取等效载荷作为单元载荷向量。

其中，Fc、Fs、FV分别表示作用于单元上的集中力、面力和体力。

（6）建立节点载荷平衡方程

在整体结构中，一个节点为几个单元所共有，因此，对每个节点i，均有

其中，ui表示共有节点i（与节点i相连）的单元的集合，Tni、Ri分别表示第n单元的第i节点（假设共有的节点在单元中的编号相同）的节点力（也称内载荷）和外力（也称外载荷），因此，前述的F是T（内力）和R（外力）之和。

（7）建立边界条件

1）力条件

边界上的单位面积的外载荷的面力Rs等于内载荷的面力Ts。

2）位移条件

（8）计算节点应力

根据节点载荷平衡方程和边界条件，首先，求解式（17）得到位移λn，然后，根据式（18）计算各单元的节点力扩展向量Fn，根据式（16），计算各单元的单元应力向量δun，从而预测出销钉拔销的受力分布。

2 基于有限分析模型的寿命预测SWT模型

销钉拔销系统的疲劳主要是以销钉的微动疲劳为主。微动疲劳是一种常见的接触疲劳现象，它发生在两个表面紧密配合并有微小的相对运动时。这种运动会在接触区域产生高应力和高应变，从而引起表面的损伤和裂纹。销钉拔销系统作为销钉拔出过程使用的一种重要器件，反复使用受到微动疲劳的影响，其寿命会因此降低。本文采用临界平面法中的SWT模型来建立销钉拔销疲劳受损的剩余寿命预测模型[10]。

临界平面法是一种分析裂纹萌生的方法[14]，基本思想是：将裂纹萌生问题转化为寻找临界平面和综合参数的问题，在复杂应力状态下，存在一个最有利于裂纹萌生的平面，称为临界平面，在有限分析模型基础上，通过在有限单元积分点计算一个综合参数，可以比较不同截面的裂纹萌生倾向，从而预测工程构件的疲劳寿命。

2.1 基于有限分析模型的微动损伤预测模型

裂纹的萌生通常发生在一个特定的危险平面上，这个平面可以用一个综合参数来描述，称为临界平面参数。临界平面参数可以反映材料在复杂应力状态下的疲劳性能，有多种形式，如SWT模型、FP模型、SSR模型、MSSR模型等[15]。本文采用SWT模型建立销钉拔销系统微动损伤预测模型，如式（21）。根据销钉拔销系统的销钉微动损伤度，从而预测出销钉拔销系统的耐力强度。

式中:D为微动损伤参量，δmax为最大应力,εa为应变幅值。

2.2 基于微动损伤模型的疲劳寿命预测模型

微动疲劳寿命预测模型的核心在于解决接触问题[13]。接触表面的应力和位移是微动疲劳的两个主要控制因素。为了提高应力和位移计算的精度，本文采用有限元分析模型进行计算，然后根据临界平面法的SWT模型，建立了微动疲劳寿命预测模型。微动损伤疲劳是一种由于微小的位移或变形而导致材料失效的现象。微动损伤疲劳的影响因素众多,包括材料的性质、微动损伤幅度、作用力幅值及其频率、温度、环境等。基于微动损伤的疲劳寿命预测模型可以表示为:

式中:A和m为材料特性相关的系数，δ为应力，f为力的频率。

2.3 强度与寿命预测流程

销钉拔销系统的强度与寿命预测流程如图1所示，通过建立销钉拔销系统的有限元分析模型，计算出销钉拔销系统的节点力和单元应力分布，在此基础上，计算销钉拔销系统微动损伤度和疲劳寿命。

图1 强度与寿命预测流程图

3 仿真与试验验证

3.1 拔销过程的销钉应力分布仿真

现在常用的有限元软件有Ansys、Abaqus、Cosmos和Marc等。Abaqus是一款专业的有限元分析软件，在国际上的知名度都是首屈一指的，完美地融合了同类软件中的优点，拥有各种类型的材料模型库，可以模拟典型工程材料的性能，适用于相对简单的线性分析和复杂的非线性分析。本文使用Abaqus 2022对销钉拔销系统的销钉拔销过程进行有限元分析仿真计算。

仿真的销钉拔销系统的结构示意图如图2所示，销钉是构成销钉拔销系统的核心元件，销钉为圆柱体金属构件，仿真的大型水轮机轴联的销钉拔销系统的销钉为6个，呈等间隔圆环设置，使用6个销钉联接的大型水轮机轴联系统的Abaqus 2022仿真模型结构图如图3所示，仿真的销钉拔销系统的销钉长度400 mm，直径120 mm，弹性模量为206 MPa，泊松比为0.3，销钉拔销系统在拔销过程中的外载荷（外力）900 MPa，属于面力。销钉拔销系统拔销过程的销钉云图如图4所示。由图4可以看出，在销钉的4处出现较高应力，此应力集中现象与环带的微动疲劳问题有关，符合实际构件破坏情况。

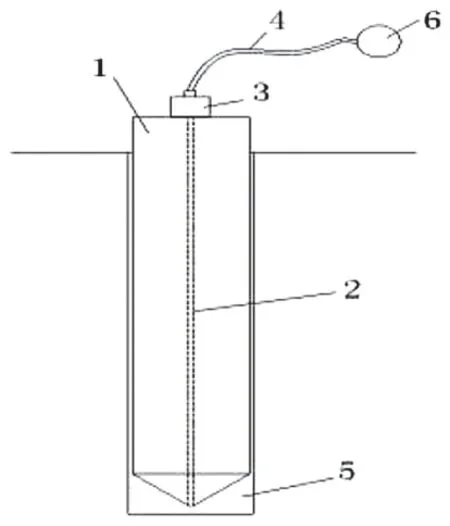
图2 销钉拔销系统的结构示意图

图3 销钉联接的大型水轮机轴联系统的Abaqus模型

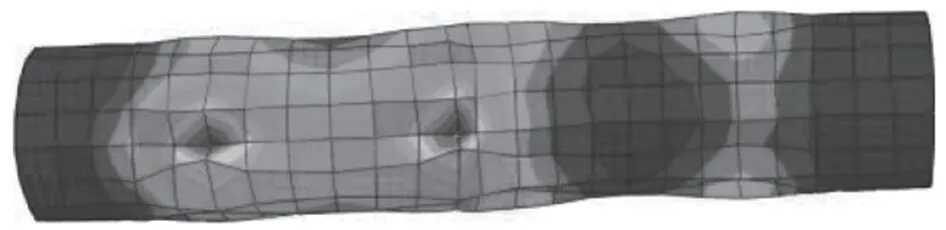
图4 销钉拔销过程的销钉应力分布仿真模型

3.2 销钉拔销寿命的仿真和实验

销钉拔销系统仿真与实验的销钉采用锻钢35CrMo材质，销钉的化学成分及机械性能参数见表1。销钉拔销系统仿真，采用Abaqus 2022+Maltlab仿真软件。销钉拔销系统的实验过程，采用电子式万能试验机模拟销钉拔销，采用直读光谱仪进行监测，试验在室温空气介质中进行，仿真和实验结果如图5和图6所示。图5为销钉拔销系统的销钉SWT参数与疲劳寿命的关系曲线，图6为销钉疲劳寿命的仿真和实验预测结果。

表1 销钉的化学成分与机械性能参数

图5 销钉SWT参数与疲劳寿命的关系

图6 销钉疲劳寿命的仿真和实验预测结果

由图5可以看出，SWT参数的销钉疲劳数据拟合的效果较好。由图6可以看出，实验预测结果基本上均布在试验结果的两侧，效果较为理想，销钉疲劳寿命实验与仿真预测的误差因子小于1.5，仿真预测结果小于实验结果，仿真预测结果偏于保守，但是与实验结果的偏差较小，由此可见，本文所研究的寿命预测模型具有较高的疲劳寿命预测精度。

4 结论

本文旨在利用有限元法和SWT对大型水轮机轴联销钉拔销系统的强度和寿命进行预测。通过理论分析和仿真与实验，可以得到以下结论：

（1）基于有限元分析，可以确定销钉拔销系统的销钉是否在承受负载时会发生塑性变形或破坏。如果超过了材料的屈服强度，销钉拔销系统可能会发生塑性变形。如果应力达到了销钉拔销系统的破坏强度，销钉可能会发生破坏。

（2）建立的销钉拔销系统疲劳寿命预测SWT模型，在估算疲劳寿命时，以临界平面上的损伤为主，同时了考虑材料的总体损伤程度，适用于变幅或随机多轴载荷情况下的多损伤平面情况的寿命预测。以临界平面上最大剪应变幅、正应变幅为参数建立微动损伤和疲劳寿命预测SWT模型，能够得到较高的预测精度，误差因子小于1.5。

（3）基于有限元法和SWT的预测方法，可以较高精度地评估销钉拔销系统的强度和寿命。该方法为大型水轮机轴联销钉拔销设计和工程实践提供了重要的技术支持，能够提高水轮机的可靠性，降低运维成本，并减少检修事故的发生。