基于多模型融合的水轮机振摆合理性分析及预测

王晓兰，胡思宇，管毓瑶，刘洋成，魏棕凯

（大唐水电科学技术研究院有限公司，广西 南宁 530007）

0 引言

水轮发电机组的安全稳定运行，对于水电站至关重要。在机械、水力、电磁因素耦合及机械部件老化等多种原因的复合影响下，水电机组产生的故障大多以振摆形式表现出来，因此振摆信号可以直观地对机组运行状态进行表征[1-5]。

目前，水轮发电机组的在线监测系统对关键指标进行越限告警的设定。但是阈值的设定往往比较高，也仅仅考虑单一指标的越限，机组预警的精确度不高，误报和漏报的情况时有发生。在稳定运行区域，水轮发电机组的各个监测指标仍会受到水头和励磁电流等工况的影响，直接采集计算的监测指标变化率无法准确反映设备状态的真实情况[6，7]。

目前，对于水轮机振摆分析存在以下问题：（1）海量的在线监测系统没有统一的管理和维护办法，前端采集到的数据没有进行深入分析和缺乏专业技术人员的技术支持。（2）目前所采用的水轮机状态监测和预警是通过设定固定阈值、计算变化率的方式，这样的方式存在误报、预警不及时的问题。（3）水电机组振摆监测信号受到运行环境、工况变化等多种因素综合影响。其信号是复杂非线性的，仅仅考虑单一因素无法准备预测振摆信号。

本文研究一种基于多模型融合的水轮机振摆分析预测的方法，通过这种方法，能自动进行水轮机振摆幅度实时预测，并对振摆的振幅进行合理性判断，有效的识别出超出正常范围的情况，进一步的进行告警。

1 方案设计

本文提供的振摆分析预测方法，通过最小二乘将SVR、LightGBM和XGBoost进行融合，采用融合后的模型，对水轮机振摆数据进行分析预测，对异常的振摆值进行实时报警，从而达到故障诊断辅助决策的目的。具体如图1所示。

具体步骤主要分为以下6部分：

（1）获取历史的机组振摆相关数据，并将数据表整合。

（2）将预处理完成的数据进一步处理为训练集合。

（3）提取出训练集合中的与振摆相关的数据，分别输入SVR机器学习模型、LightGBM模型和XGBoost模型进行训练。

（4）对三个模型的结果进行最小二乘拟合，得到三个模型的权值分配，形成融合模型，使预测数据贴近真实状况，得到能够精准预测振摆结果的模型。

（5）将在线监测的振摆相关数据输入训练好的融合模型，得到预测出的振摆并作为该工况下振摆的标准值。

（6）将采集的振摆数据与标准数据做对比，标记异常数据及异常等级。其中异常等级的划分遵循以下原则：当振动值与摆度值小于40 μm时，若幅度大于预测值10 μm以上，判断为二级幅度异常，若幅度大于预测值20 μm以上，判断为一级幅度异常。当振动值与摆度值大于40 μm时，当幅度大于预测值的10%~25%，判断为二级幅度异常；当幅度大于预测值的25%时，判断为一级幅度异常。

2 相关原理

2.1 SVR

支持向量回归（SVR）是一种基于支持向量机（SVM）的用于回归的机器学习方法[8]。本文基于SVR，结合振摆及相关测点数据，通过在样本空间中找到一条曲线并使所有数据点都尽量离该曲线足够近，以实现对振摆数据拟合回归功能[9]。其模型如图2所示。

图2 支持向量回归模型

当存在n个输入变量时，假设一个非线性估计模型：

其中，b代表偏差，w为权重向量，φ(∙)为高维特征空间[10]，xi为输入向量。

SVR的最终目的即通过最大化间隔带的宽度与最小化总损失来优化模型，求解得到f(x)中的w和b，则在求解过程中，需满足一定的约束条件，即：

实际应用中，ε设置太小无法保证所有样本点都在间隔带中，ε太大回归超平面会被一些异常点带偏，为此SVR允许每个样本（xi，yi）添加松弛变量ξi以避免优化问题求解不可行。此时SVR目标函数表示为[11]：

式中，C为惩罚系数，C过大或过小都不恰当，本文取值C=1以获得较好的拟合效果。

2.2 LightGBM

LightGBM以决策树为弱分类器，在传统梯度提升树（Gradient Boosting Decision Tree，GBDT）的基础上，在生长策略上做了优化。优化方式包括特征直方图、单边梯度采样、互斥特征捆绑和Leaf-wise。

假设训练数据集为{（x1，y1），（x2，y2），…（xN，yN）}，初始化分类器其中h0（x）为选定的首个基学习器，并设定T个基学习器的训练目标，每个基学习器的计算方法如下。

（1）当前损失函数的负梯度myi的计算公式如下：

（2）拟合myi得到当前基学习器ht的参数：

（3）最小化损失函数得到当前基学习器的权重：

最终的分类器Ft（x）即为每个基学习器的加权和：

2.3 XGBoost

XGBoost同样以决策树为弱学习器，其集成模型如式（8）所示。

K是基学习器的数量；R代表基学习器的集合空间；fk表示集合R中的一个函数。

XGBoost的目标函数如下：

其中T为叶子结点数量；γ代表惩罚函数系数；ωj代表叶子结点的权重；λ代表正则化惩罚项系数。

2.4 最小二乘权值融合

为增加模型的鲁棒性，将三种模型进行最小二乘权值融合，假设SVR预测结果为y1，LightGBM预测结果为y2，XGBoost预测结果为y3，那么融合后模型的预测值y'符合以下约定：

其中β为SVR权值占组合权值的比例，γ为LightGBM占组合权值的比例，λ为XGBoost占组合权值的比例，满足：

对综合权值进行最优求解：

3 实验分析

实验时选取水轮机水导摆度和顶盖振动作为预测目标，经过专家经验筛选49个相关特征后，采用皮尔森系数相关性分析后，选取25个高相关特征作为特征集合。将历史数据拆分为训练数据和测试数据，分别采用SVR、LightGBM和XGBoost进行训练和测试，进一步的，为增加模型的鲁棒性，采用最小二乘法将三种模型进行权值融合，融合后的权值分配如表1所示。

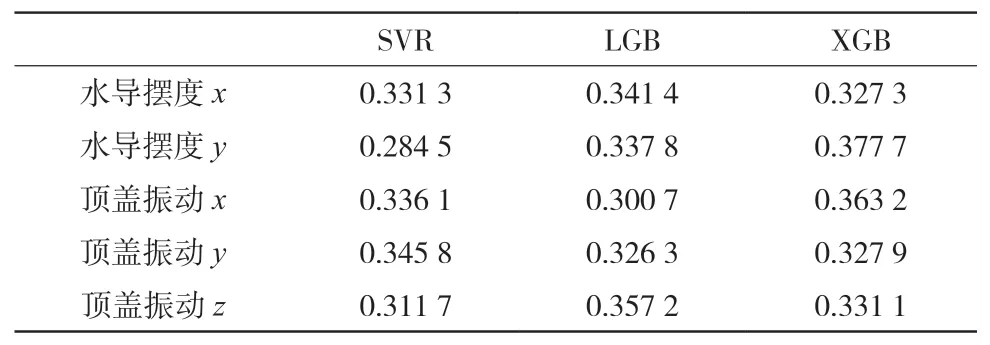
表1 融合模型权值分配结果

将所有模型的预测结果选取其中100个点进行绘图，实验结果如下：

从图3可以看出，四种方法在测试集上的预测结果与真实值的趋势保持一致，说明四种方法对于振摆的预测均有良好的效果。为进一步对模型效果进行评价，决定系数R2指标对四种模型进行评价，R2得分反映因变量的全部变异能通过回归关系被自变量解释的比例，表示为：

图3 不同模型预测结果与真实值对比图

其中，yi表示真实的观测值，用表示真实观测值的平均值，用表示预测值，MSE为均方误差，Var为方差。

R2评分的取值范围为[0,1]，值越趋近于1表示模型拟合效果越好[12]。其结果如表2所示。

表2 不同模型评价结果

从表2可以看出，三种方法在水导摆度和顶盖振动上的R2系数均大于0.95，说明三种模型均能有效预测振摆值，但通过对比，经过最小二乘融合后的模型，R2评分可以达到0.98以上，有显著的效果提升。

将融合模型进行封装后实时预测振摆值，并按照相关规则对异常数据和对应的告警等级进行记录。

4 结论

（1）在振摆预测分析的问题上，采用专家经验和特征工程技术共同选定特征集合可以综合考虑影响振摆变化的因素，全面准确地提供有效的数据基础。

（2）本文所采用的基学习器SVR、LightGBM和XGBoost均能够有效地对振摆值进行预测，模型R2评分可以达到0.95以上。

（3）本文所研究的基于多模型融合的振摆分析模型在基学习器的基础上，通过基学习器的不同表现进行权值分配，融合后的模型能够更加有效和稳定的预测振摆，R2评分达到0.98以上，对比单一模型的效果，有了显著的优化与提升。

（4）本文所研究的方法可以拓展适用于其他部位的预测，例如水轮机瓦温预测等。