水电机组设备测点劣化趋势分析方法研究
张太衡,刘志佳
(1.华电电力科学研究院有限公司,浙江 杭州 310000;2.福建华电福瑞能源发展有限公司池潭水力发电厂,福建 三明 353000)
0 引言
在水电远程诊断技术的研究应用过程中,发现机组问题是触发故障知识库[1]的前提条件,单以某些测点超限值作为触发条件还不够精确,不能排除机组在开停机、变负荷、变励磁等过程中引起的测值正常跳变现象,考虑到机组状态变化在一般情况下是缓变过程,因此系统需具备针对测点变化趋势的分析功能。区域级的水电远程诊断系统接入机组设备较多,对大量测点一一进行离线趋势分析耗时耗力,应滚动提取历史数据做趋势回归分析,实现测点在线趋势预警,提高自动化程度,对发出趋势预警的测点再进行离线趋势预测,掌握未来一段时间内的走势,更有针对性且减轻了系统的计算压力,通过测点趋势预警和趋势预测的结合,提供完整的趋势分析功能。
通过对机组测点在历史运行趋势的分析,对测点变化趋势做出判断,对超过规定趋势预警限值的测点进行预警,在对测点变化趋势做出判断时,最重要的是趋势回归,目前趋势回归的方法比较多,如线性回归、多项式回归、逻辑回归、逐步回归、岭回归等,寻找简单实用的回归模型是趋势预警的核心。
除了对测点历史趋势的研究,还需要对测点未来一段时间内的走势做出预测才能完善整个趋势分析功能,趋势预测的样本数据以实际运行过程中产生的数据为基础。趋势预测的核心在于预测模型的研究,常见的应用于工业领域的预测模型包括自回归模型(AR)、移动平均模型(MA)、差分自回归移动平均模型(ARIMA)[2]、灰色模型[3]、神经网络模型[4]等,但目前这些预测模型在水电机组设备劣化趋势研究中应用的还不多,寻找实用高效的预测模型并应用到水电机组运行趋势分析中,获得测点未来一段时间内可能的变化趋势,对设备运行管理人员有一定的指导意义。
1 工况划分
趋势分析要以一定的历史样本数据为基础,水电机组在运行的过程中会出现多种运行工况,如开停机过程、稳定运行过程、变负荷过程等,实际的稳定运行过程又可分为不同水头和负荷下的运行过程,拿不同工况混合的历史运行数据做趋势分析没有实际意义,因此要对机组的运行数据做工况区分管理。
根据国标 GB/T 32584-2016中水电机组稳态运行工况的定义,要求机组流量(有功)、水头等主要参数保持在±1.5% 以内[5],根据机组的实时负荷、转速、断路器状态,将机组工况区分为开机过程、关机过程、稳定运行过程、负荷变化过程、停转以及其他。

图1 机组运行工况划分
(1)机组转速判断:V(t)<0.01×V额定时为停机态;V(t)<1.01×V额定时为其他;V(t)∈[0.01×V额定,1.01×V额定]进行转速变化趋势判断。
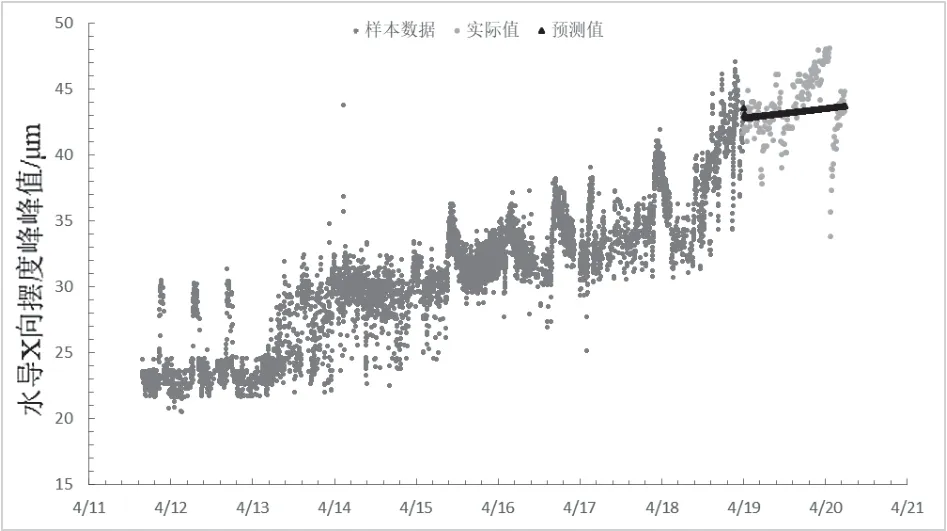
(2)转速变化趋势判断:abs(V(t)-V(t-1)>0.02×V额定且V(t)>V(t-1)时转速变大,为开机过程;abs(V(t)-V(t-1)>0.02×V额定且V(t) (3)负荷是否稳定判断:abs(P(t)-P(t-1)<0.015×P额定为稳定运行状态;abs(P(t)-P(t-1)≥0.015×P额定为变负荷过程。 以一定时间间隔自动对机组进行工况判断,形成运行工况记录表,如表1。 表1 运行工况记录表 在某一工况下作趋势分析时,按照表1运行工况记录,提取该工况的运行时间段,将运行时间段内的数据作为样本数据。 按照线性回归的思想采用最小二乘法[6]提取测点历史样本数据的变化趋势,线性回归后表达式为: 式中:x为样本数据的点数;y为样本点的值。 线性方程中a为斜率,可表征该段时间内历史样本数据的变化程度,将斜率与设定的趋势限值作比较,超过限值时,测点发出预警,但在实际应用过程中,所提取的样本数据的长度对线性回归的斜率影响很大,提取的数据较少时斜率可能很大,但放到长时间尺度内,线性回归后斜率又可能很小,不足以触发预警条件,因此要对线性回归后的斜率作标准化处理。 考虑到机组的实际运行情况,按照提取的历史样本数据的时间间隔,计算出取数周期内有多少个数据点,将线性回归后的斜率处理为标准的变化幅度,则预警表达式为: 式中:n为提取到的实际点数,m为数据总点数,V1、V2为趋势预警限值下限、上限。 根据实际情况的不同,可设置多个趋势预警区间,如缓慢上升趋势、快速上升趋势、缓慢下降趋势、快速下降趋势、稳定趋势,趋势预警的实现采用滚动趋势回归的方式,不断提取最近一段时间内的历史样本数据,以此来保证预警的不间断和可靠性。 在某一稳定工况下时,对发出趋势预警的测点进行趋势预测,预测未来一段时间内的变化趋势,根据运行工况记录表,筛选出某工况下的历史数据组成时间序列,筛选出的数据时间不连续或者间隔不一致,按照插值法处理成等间隔的历史样本数据。 自回归模型(AR)描述当前值与历史值之间的关系,用自身的历史数据进行预测,自回归模型必须满足平稳性的要求,p阶自回归过程的公式定义: 式中:yt为当前值;μ为常数项;p为阶数;γi为自相关系数;εt为误差。 移动平均模型(MA)关注的是自回归模型中的误差项的累加,将时间序列看成白噪声序列的线性组合,q阶自回归过程的公式定义: 式中:yt为当前值;μ为常数项;q为阶数;θi为误差系数;εt为误差。 自回归移动平均模型(ARMA)是自回归模型(AR)和移动平均模型(MA)的结合,得到自回归移动平均模型: 将ARMA模型和差分法结合,得到差分自回归移动平均模型ARIMA(p,d,q),其中d是需要对数据进行差分的阶数。ARIMA模型关键是确定p,d,q三个参数,样本数据不平稳时,通常进行差分化处理,差分阶数d一般取1,参数p、q可通过最小化信息量准则(AIC)[7]确定。 (1)样本数据提取:根据始末时间和工况条件(功率、水头)在运行工况记录表中寻找满足要求的时段,并根据提取到的时段获取测点在该时段内的原始数据,将数据按照等间隔插值处理; (2)样本数据平稳性检验:单位根检验是指样本序列中是否存在单位根,如果存在单位根就是非平稳时间序列,会使回归分析中存在伪回归,采用扩展迪基-福勒检验(ADF)[8]测试模型是否存在单位根; (3)样本数据差分化处理:如果原始样本数据没有通过ADF检验,则观察样本数据的周期性,机组测点原始数据周期性并不明显,通常按照一阶差分(d=1)即可,检验得到稳定的时序数据; (4)ARIMA模型定阶:根据AIC准则实现程序自动化定阶,确定ARIMA模型p、q阶数,当q=0时选择AR模型,p=0时选择MA模型,均不为0时选择ARMA模型; (5)ARIMA模型预测:根据样本数据的时间间隔,输入预测的步数,获得预测值。 本文以国内某电厂1号机组测点“水导X向摆度”为研究对象,选取日期2019/4/11到2019/4/18内额定负荷12万kW,水头70 m稳定工况下测点的原始数据作为样本数据,以分钟为间隔插值处理成等间隔样本数据,如图3所示,应用python中的adfuller模块对样本数据进行ADF平稳性检验。 图2 ARIMA模型建模过程 图3 样本数据 ADF原假设为序列存在单位根,即非平稳,对于平稳的时序数据,就需要在给定的置信水平上显著,拒绝原假设。检验结果如表2所示,ADF统计值显著大于3个置信度(1%,5%,10%)的临界统计值,说明是接受原假设,即样本数据不平稳。 表2 样本数据平稳性检验结果表 对样本数据进行一阶差分处理,差分后数据如图4所示,再进行ADF平稳性检验,检验结果如表3所示,ADF统计值显著小于3个置信度(1%,5%,10%)的临界统计值,说明是拒绝原假设,且p-value接近于0,即一阶差分后样本数据平稳。 表3 一阶差分后平稳性检验结果表 图4 一阶差分后样本数据 经过一阶差分后的数据是平稳的,再根据AIC准则对ARIMA模型定阶,定阶结果为p=4,q=9,即确定采用ARMA模型,预测未来200个数据点的值(steps=200),预测结果如图5、图6所示,由于原始数据的波动性不规律,摆度测点值抗干扰性较弱,预测出的结果波动性不明显,只能大致预测出未来的走势。 图5 预测结果 图6 预测结果和实际值 集成趋势预警和趋势预测的机组设备测点劣化趋势分析方法能够有效避免超限值报警的单一性,考虑了机组在缓变过程中的趋势变化,利用线性回归构建滚动趋势预警工作方式,对趋势预警测点采用ARIMA模型建模,预测测点未来走势,该劣化趋势分析方法较为简单实用,可应用于电厂水电机组诊断系统中,对机组检修、运行具有一定的指导意义。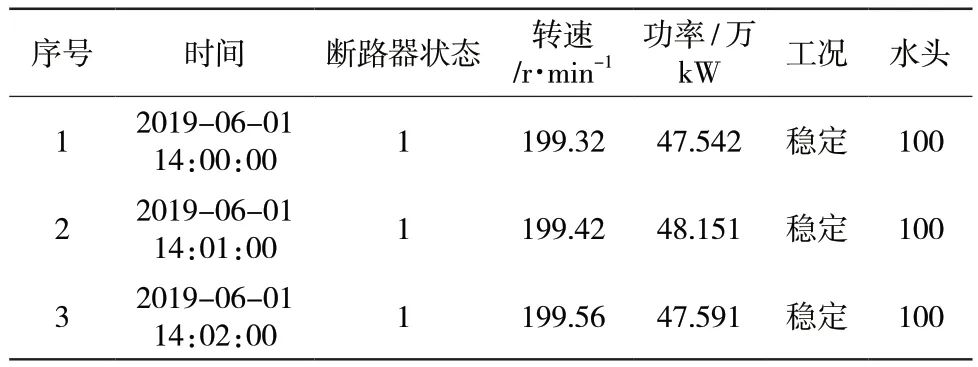
2 趋势预警
3 趋势预测
3.1 差分自回归移动平均模型(ARIMA)
3.2 ARIMA建模
3.3 算例






4 结论

