区域降水量反演下水库调蓄能力空间位置参数辅助预测

乔俊明

（包头市水库管护中心，内蒙古 包头 014030）

0 引言

水库是建设在河流流域周围的建筑实体，其建设作用是缓解水资源时空分配不均匀的问题，同时实现拦洪蓄水、灌溉、发电等功能。水库的建设需要保证水库具备封闭的蓄水空间，且蓄水空间足够大，水库区域内具有良好的水力传导条件，也就是水库与周围水流环境之间存在高低落差；水库能够在人工干预的情况下实现水资源的采集与补充[1]。在满足上述3个条件的情况下，可以建造水库，并按照水库的建设规模将其分为小型水库、中型水库和大型水库。一般来讲，水库的运行主要通过大坝、溢洪道和防水建筑物等组成部分的协同，实现水库的作用和功能。

在水库调蓄能力允许的情况下，通过对调蓄方案的合理设计与实施，能够提升水库的实际效益和作用价值。水库调蓄能力指的是水库所能提供和容纳的水资源最大容量，水库调蓄能力可以分为水资源调度能力和蓄水能力两个方面。预测水库调蓄能力对于制定流域防洪策略以及区域水资源可持续利用战略都有重要意义，因此提出了水库调蓄能力预测方法。从目前的发展情况来看，现有的水库调蓄能力预测方法由于未考虑到降水对水库的影响，因此普遍存在预测误差大、应用价值低的问题，为此，提出区域降水量反演下的水库调蓄能力空间位置参数辅助预测方法，通过增加调蓄能力的考虑参数实现调蓄能力预测精度的提升。

1 水库调蓄能力预测算法设计

1.1 水库组成结构及空间位置参数分析

水库由水源系统、引渗回灌系统、蓄水系统、排水系统组成，具体的组成结构如表1所示。

以表1中表示的水库组成结构模块为基础，通过分析各个结构之间的空间位置参数以及工作模式，构建相应的数学模型，空间位置参数确认模型表达式如下：

式中T为导水系数，该指标的具体取值公式为：

式中h（x，y）和d（x，y）分别为水库浅水层和含水层的底板标高，K为渗透系数。另外公式（1）中变量qj（t）和Q（t）分别为j河段t时刻的河流渗漏补给量和i口的开采量，参数ε和μ对应的是降水入渗强度和给水度[2]。在考虑水库周围地形和水文地质条件的情况下，确定公式（1）中各个变量的具体取值，为水库调蓄功能模拟提供环境支持。

1.2 卫星数据反演区域降水量

利用雷达结合雨量计求降水空间分布的方法，估算水库联合雨量[3-6]。先确定卫星反演降水数据和气象台站降水比例的观测值：

式中，λ为常数，Rk和Sk分别为观测降水量值及卫星反演降水量；n为研究区中的气象台数量[7]。在此基础上得出降水量的估算公式为：

公式（4）的计算结果为第(i,j)网格的降水量估算结果，表示降水量的空间分布系数，变量Si，j为当前网格的卫星反演降水量[8]。按照上述方式通过相关数据的采集与处理操作，得出目标区域降水量的估算结果。

1.3 水库水位极限值数值模拟

随着降雨量的增多，水库中存储的水量也逐渐增多，水库水位随之上升。当水库中的水位接近极限值时，采用底孔的闸门泄出多余的洪水，将其调度到其他水库或河流环境中。水库调蓄功能的模拟过程如图1所示。

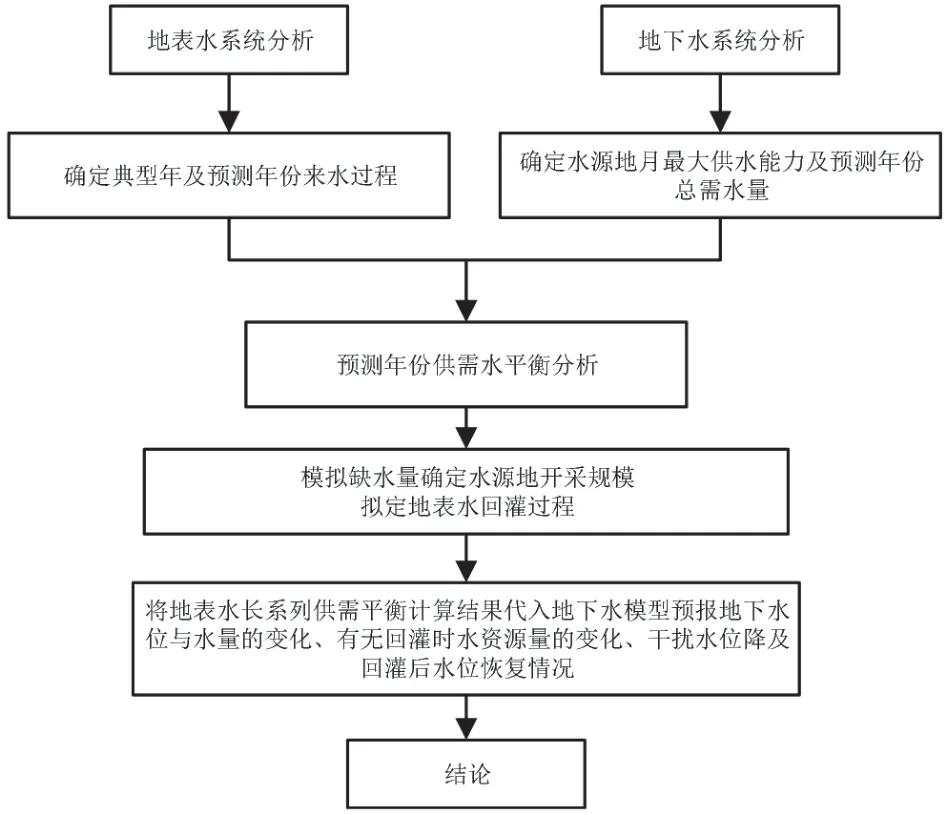
图1 水库调蓄功能模拟流程图

水库中的水资源入库后，形成水波运动，其水力学特性为明确渐变非恒定流，其运动规律可用圣维南方程描述：

式中，x、t分别表示距离和时间；A、Q、Z、u分别表示过水断面的面积、流量、水位和平均流速；hf表示摩擦阻力损失的水头。另外参量g为重力加速度，为方便计算取值为常数。通过对连续方程的求解，完成对水库水位极限值的数值模拟。

1.4 确定区域降水下水库调蓄能力预算指标

水库调蓄能力预测是根据水库当前的运行状态，对事物的因果关系进行分析，来判断结果。

预测水库调蓄能力的目的有两个：①估计每个水库各输入项和半控制输入量的可控制输入量和输入量的合成量，以确定对水库的人为干预作用；②求算水库输出项对预先设定输入的响应变化，以评估水库运行对环境的影响。由此基于区域降水量确定水库调蓄能力预算指标。

1.4.1 水库库容量

水库库容量指标是水库的主要蓄水场所，其大小直接反映了水库调蓄能力的强弱，水库库容包括潜水含水层和承压含水层库容两个部分，其结构如图2所示。

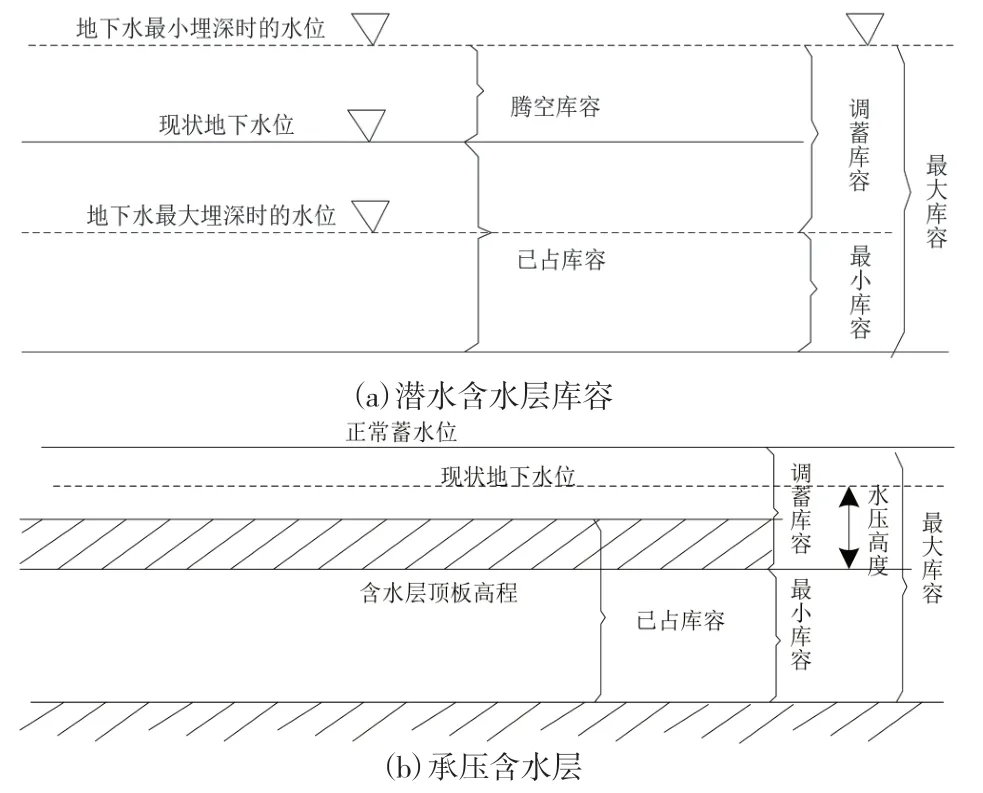
图2 库容划分示意图

根据图2中表示的水层厚度来计算水库的库容量，计算公式为：

式中变量γ、δ和θ分别表示水库土壤容重、厚度和含水百分率[9]。在构建的水库模型中，通过对水库结构以及材料参数的求解，可以得出库容量指标的求解结果。

1.4.2 水库蓄水位

水库的特征水位包括现状水位、调蓄上/下限水位等[10]。其中现状水位是指现行地下水位的分布状况，它直接决定水库调蓄能力的大小，而底部边界则根据所研究区域的水文地质条件，选取中更新底板作为地下水库底水容量的计算依据。水库特征水位的分布情况如图3所示。

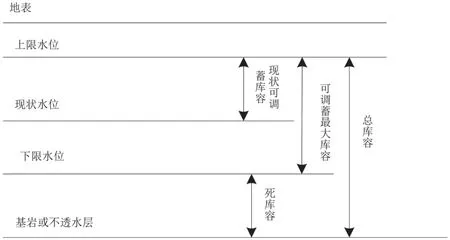
图3 水库特征水位分布示意图

特征水位指标中现状水位和调蓄上限水位的计算公式如下：

式中hp、h1和h2分别表示的是土壤毛细水强力上升高度、毛管水饱和区高度和根系集中层深度，Δz为安全超高。然而在此次调蓄能力预测中考虑了降水量的问题，因此将现状水位的计算公式调整为：

式中Sw为水库底面积，将公式（4）中的降雨量估算结果代入到公式（8）中得出现状水位的运算结果。同理可以得出特征水位中其他指标的量化计算结果。

1.4.3 最大下泄流量

最大下泄流量是评价该库区蓄水能力的最直接指标，在最大下泄流量计算中，最关键的问题是蓄水体积的确定[11]。最大下泄流量的计算公式如下：

公式9中μ和v*分别为蓄水体积变量和给水度。其中变量μ可以通过水库特征水位与底面积相乘直接得出，在水库库容量的约束下，水库蓄水能力不得高于水库库容。

同理结合水库引渗回灌系统的可容纳量以及当前的水库蓄水状态，可以得出水库库容量、水库蓄水位、最大下泄流量的最终估算结果。

1.5 实现水库调蓄能力预测

基于上述指标，完成水库调蓄能力预测。

（1）水库调蓄能力是在实际工程中，在限定的条件下，水库实际能提供的水量。水库的调蓄能力分为有回补时调蓄能力和无回补时调蓄能力[12]。以埋深不超过水库调蓄下限水位为界限，基于空间位置参数确认模型，采用试算法使水库埋深接近或等于调蓄下限水位，此时的开采量即为水库的最大调蓄能力。

（2）确定下限调蓄水位时的调蓄容量为水库的最大调蓄能力。

1）水库采空区不采用人工回补开采，当地下水埋深与调蓄下限水位相等时，此时开采井的出水量为无补水水库的最大调蓄能力。

2）在水库补注区，采用固定流量回补方式，对水库示范区进行人工回补。当地下水埋设深度等于调蓄下限水位时，水库示范区地下水回补采用定流量回补。

3）在无人工回补和有人工回补两种情况下，考虑降水量对调蓄能力的影响，输出水库的可蓄水量指标和调度能力指标的计算结果，由此完成对水库调蓄能力的预测。

2 实例分析

以测试考虑降水量的水库调蓄能力预测算法的预警精准度为目标，选择广东省高州市南山水库作为研究对象设计实例分析试验，并通过对调蓄能力预测指标与实际指标的比对，计算出预测结果误差，预测误差越小证明预测算法精准度越高。利用VisualMODFLOW作为本文空间位置参数确认模型和水库水位极限值数值模型的数据采样模型软件。

2.1 研究区域概况

广东高州市南山水库位于广东省西南部的高州市镇江镇，降雨年内分布不均，夏、秋季多雨，冬、春季少雨。南山水库水系未设置水位站、流量观测站。通过实际核查广东省水文局有关水文参数，采用广东省综合单元线法和推论公式法对设计洪水进行了计算。南山河区之间的洪水叠加下，南山水库的集雨面积超过12.2 km2，占南山水库总集雨面积的24.4%，在目前的计算中，对南山水库的调蓄排水功能影响较大，因此对南山河区间的洪水进行了计算。据统计，该流域年降雨量有6~8次，一年12个月内均出现暴雨天气，但暴雨、大暴雨或特大暴雨以汛期为主，其中前汛期多为暴雨，后汛期多为大暴雨和特大暴雨。每年4~6月西南季风盛行，如遇南下冷空气，在全流域形成暴雨；7~10月，由于西南季风和东南季风共同影响，台风盛行，尤其是7~9月台风频繁发生。汛期结束时，冷、高压南侵时，常有大暴雨发生。根据有关水文图集和资料，查明该工程区多年平均径流深度为800 mm，径流深变幅为800~1 000 mm，其变化系数为0.35~0.38。区域分布特征与降雨量基本一致，从东北向西南减少；全年径流年径流量的年际变化与降水量基本一致，存在明显的年际变化大和年内分布不均匀的特征：径流深度为1 000 mm，丰水年、平水年和枯水年分别为1 000 mm、800 mm和520 mm，丰枯年径流深度相差1.92倍。

2.2 设置降水变量

由于区域降水很难实现人为控制，因此此次实例分析试验选择抽水试验的方式，并根据广东高州市南山水库研究区域的降水特点设置具体的降水变量。水库区域的各历时点暴雨参数如表2所示。

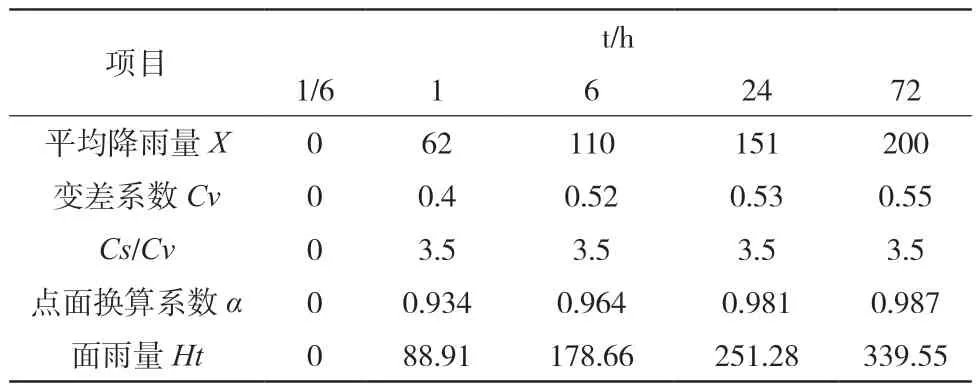
表2 点降雨参数表

表2中Cs表示的是点降水量。按照表2中的降水规律等比例的设置抽水试验中的降水变量。

2.3 选择预测效果测试指标

试验中设置预测误差作为试验的量化测试指标，其数值结果可以表示为：

式中，xforccast和xact分别为水库调蓄能力指标的预测值和实际值，实验中设置的调蓄能力预测指标为正常蓄水位、水库库容和最大下泄流量。另外公式（10）中|·|为绝对值计算符号，保证预测误差计算结果始终为正数。

2.4 试验过程与结果分析

预测时间为2020年9月1日至2021年8月31日，根据季节的预报，每年分为4个时段，共8个时段。通过确定预测时段、规定输入项和输出波动浮动，实现对预测方案的编写。通过设计的考虑降水量的水库调蓄能力预测算法的运行，分别得出调蓄能力指标的预测结果，其中水库库容和最大下泄流量指标的预测结果，如图4所示。

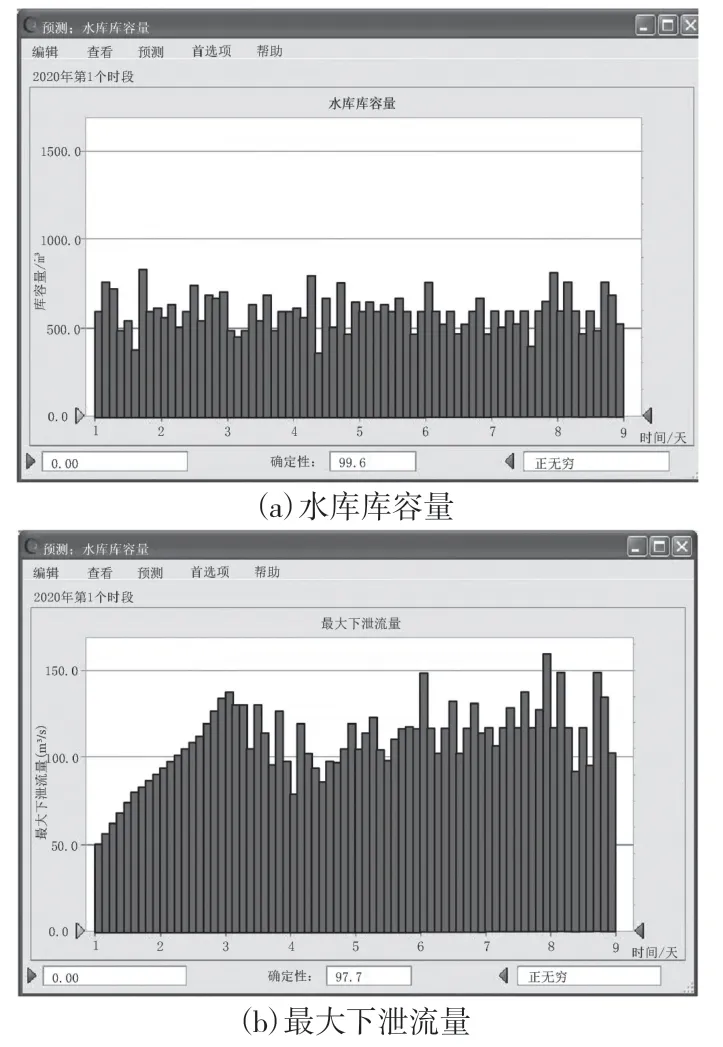
图4 水库调蓄能力预测结果

同理也能够得出调蓄能力预测算法输出的其他指标的预测结果。在选择的广东高州市南山水库中安装水位尺、测量仪等设备，用来记录水库调蓄能力指标的实际值。对比读取的实测值与预测值数据，可以得出预测误差。其中第一个预测时段中水位预测误差的测量结果，如图5所示。

图5 水库现状水位测量实景图

同理可得其他调蓄能力指标相关数据，如表3所示。

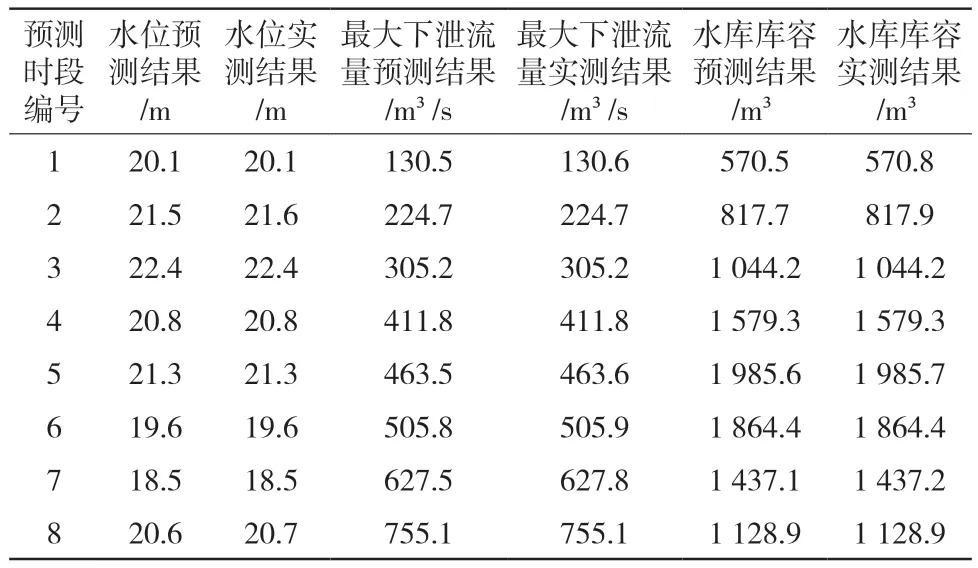
表3 水库调蓄能力预测误差测试结果

将表3中的数据代入到公式（10）中，可以得出水位、最大下泄流量以及水库库容3个水库调蓄能力指标的平均预测误差分别为0.025 m、0.075 m³/s和0.088 m³，3个调蓄指标的预测误差均低于预测标准误差0.1，满足对预测算法精度的要求。

3 结语

通过对降水量的预测与考量，在现有预测算法的基础上进行优化设计，在不考虑降水量的情况下，预测出的水库调蓄能力普遍偏小，能够将预测误差控制到允许范围内，为水库管理以及防洪工作提供有价值的参考数据。