改进高斯柯西差分进化算法求解热电联产经济调度

陈 旭，沈安宁，李康吉

（江苏大学电气信息工程学院，江苏 镇江 212013）

0 引言

传统的火力发电厂用煤发电，效率很低，在转化过程中，存在大量的热量流失和浪费。热电联产机组既能发电又能供热，将损失的热量重新利用，提高了能量转换效率。经过二十多年的发展，热电联产技术受到研究者越来越多的关注。根据中国电力规划设计院的数据，截至2021 年，中国热电联产总装机容量已达264.6 万kW，占全国火电总装机容量的6.3%。其中，工业热电联产占比最高，达87.5%，商业和居民热电联产占比分别为10.6%和1.9%。与传统火力发电相比，热电联产技术可实现高达90%的能量转换效率，并减少13%～18%的污染物气体排放。

热电联产系统由发电机组、热电联产机组和供热机组组成。热电联产经济调度（combined heat and power economic dispatch，CHPED）的目的是使总生产成本最小化，同时满足不同的运行约束，包括火电厂的阀点效应、热电生产能力、需求平衡、输电损耗等。早期解决CHPED 问题通常采用传统的数学方法，如分枝定界法［1］，对偶二次规划［2］。但是传统的数学方法存在局限性，例如对于初始解比较敏感，容易局部收敛，不能处理非凸非线性问题等。

现代智能优化算法能够很好地克服传统数学方法的缺陷，因此越来越多的科研工作者使用智能优化算法进行CHPED 问题的研究，例如遗传算法［3-4］、粒子群优化［5-6］、差分进化［7-8］、社会认知优化［9］、随机分形搜索［10］、和谐搜索［11］、纵横交叉算法［12］等。

此外，为提升智能优化算法求解CHPED 问题的性能，一些学者混合两种或多种算法，设计了混合优化算法。例如，Murugan 等［13］提出了结合蝙蝠算法、人工蜂群和混沌自适应搜索策略的混合算法。Gu等［14］提出了基于生物地理学和模拟退火的混合算法。Nasir 等［15］提出了一种融合萤火虫算法和自调节粒子群的混合优化算法。Ramachandran 等［16］提出了一种混合改进的蚱蜢优化和哈里斯鹰优化的新型优化算法。

目前智能优化算法在求解复杂CHPED 问题上，仍然存在易陷入局部最优、优化精度不高等问题。为此，提出一种新型的高斯柯西差分进化（Gaussian-Cauchy differential evolution，GCDE）算法。GCDE 算法主要引入了高斯柯西变异算子和参数自适应两个策略，来提升差分进化算法求解CHPED 问题的性能。通过将GCDE 算法应用于两个CHPED 模型，验证了其具有较好的求解性能。

1 CHPED模型建立

1.1 目标函数

热电联产的燃料成本函数由纯电机组的燃料成本、热电联产机组的燃料成本和纯热机组的燃料成本组成。

式中：FC为燃料的总成本；Ci(Pi)为第i个纯电机组的燃料成本为第j个热电联产机组的燃料成本；Ck(Hk)为第k个纯热机组的燃料成本；Pi为第i个纯电机组的输出功率分别为第j个热电联产机组的输出功率和输出热量；Hk为第k个纯热机组的输出热量；NP、NC、NH分别为纯电机组、热电联产机组和纯热机组的机组数量。三种不同类型机组的燃料成本构成如下。

式中：αi、βi、γi、λi、ρi为第i个纯电机组的成本系数；aj、bj、cj、dj、ej、fj为第j个热电联产机组的成本系数；ak、bk、ck为第k个纯热机组的成本系数为第i个纯电机组的输出功率下限。

1.2 约束函数

1.2.1 电功率平衡约束

式中：PD为电负荷；Pl为第l个纯电机组的输出功率；PL为电力传输损耗，通过克朗公式［17］计算求得；Bil、B0i和B00为相关计算系数。

1.2.2 热平衡约束

式中：HD为热负荷。

1.2.3 纯电机组输出功率约束

1.2.4 热电联产机组输出约束

1.2.5 纯热机组输出热量约束

2 高斯柯西差分进化算法

2.1 基本DE算法

差分进化（differential evolution，DE）是一种基于种群的进化算法。它使用变异、交叉和选择算子来生成新的个体。每一代都保留较好的个体，达到种群进化的目的。DE 算法在解决不同领域的复杂优化问题上有多种应用，包括化工过程优化［18］、电机设计优化［19］等。基本DE 算法步骤如下。

1）初始化。

DE 算法将初始化N个个体，得到初始种群Xm,0，每个元素记为Xm,n,G（n=1,2,…,D）。

式中：Xm,0=(Xm,1,0,Xm,2,0,…,Xm,D,0)为第m个个体；分别为下限和上限；D为向量的维度；Rand为一个D维随机向量，每个元素取值在[0,1]之间。

2）变异。

种群根据式（12）进行变异生成新的变异个体Vm,G，每个元素记为Vm,n,G（n=1,2,…,D）。

3）交叉。

种群根据式（13）进行交叉生成新的个体Um,G，每个元素Um,n,G（n=1,2,…,D）的取值为

式中：Q为交叉概率；jrand为［1，D］之间的一个随机整数；rand为［0，1］之间的随机数。

4）选择。

式中：f(·)为DE 算法求解的优化函数。下一代种群中的个体通过选择操作实现，如果经过变异和交叉步骤后的个体适应度优于原来个体的适应度，则将Um,G替换Xm,G至下一代，否则保持Xm,G不变。

2.2 GCDE算法

为了改进DE 算法求解CHPED 问题的性能，提出了高斯柯西变异自适应差分进化（Gaussian-Cauchy DE，GCDE）算法。该算法在两方面做出了改进，即参数自适应策略和高斯柯西变异策略。

2.2.1 参数自适应

在DE 算法的变异和交叉过程中，有两个参数值得注意，即F和Q。F和Q固定取值无法应对不同问题的求解。因此，在GCDE 算法中，采用了自适应调节的参数策略。对每个个体Xm,G取独立的参数Fm,G和Qm,G，更新公式如下。

式中：Fm,G初值设置为0.5；Qm,G初值设置为0.9；τ1、τ2、Fl、Fu为参数，数值分别为0.1、0.1、0.1、0.9；rand1、rand2、rand3、rand4为［0，1］之间的随机数。

当选择操作成功时，即f(Um,G)≤f(Xm,G)时，保留Fm,G和Qm,G的值至下一代，否则Fm,G和Qm,G的取值分别以τ1和τ2的概率进行修改，具体修改方式参照式（15）和式（16）。

2.2.2 高斯柯西变异策略

高斯柯西变异（Gaussian-Cauchy mutation，GCM）策略主要是在基础变异步骤上，以一定概率使用高斯和柯西变异，用以增强算法的局部搜索能力。

式中：θ为概率，取值为0.05；FES为函数评价次数；FESmax为最大函数评价次数；Gaussian(·)为高斯函数；Cauchy(·)为柯西函数；GCM为高斯柯西变异后得到的个体。高斯柯西变异策略的使用概率从0 增加至0.05。GCDE 算法的流程如图1 所示。

2.3 约束处理技术

在应用GCDE 算法时，个体Xm(m=1,2,…,N)由CHPED 问题中纯电机组、热电联产机组和纯热机组输出的电能和热能组成：

此外，在优化过程中，对产生的新个体需要运行约束修复技术，获得可行解。约束修复技术如下：

1）对纯电机组Pi(i=1,2,…,NP)，容量约束修复方式为

3）对纯热机组Hk(k=1,2,…,NH)，容量约束修复方式为

XP中任一元素XP的修复方式为

XH中任一元素XH的修复方式为

3 仿真结果分析

GCDE 算法被用于求解两个CHPED 模型。为了验证其有效性，将GCDE 算法与现有代表差分算法，即差分进化算法［20］、高斯变异差分进化（differential evolution with gaussian mutation，DEGM）算法［21］和策略自适应差分进化（differential evolution with strategy adaptation，SaDE）算法［22］的结果进行比较。所有算法都运用了约束修复技术修复可行域外的个体，使其满足约束条件，且均是独立运行30 次。仿真平台为MATLAB R2016a，计算机配置参数为i5-7500 3.40GHz、8G。

3.1 系统1：7台机组

系统1 由4 台纯电机组、2 台热电联产机组和1 台纯热机组组成。该系统的电负荷和热负荷分别为600 MW 和150 MW。该系统仅考虑阀点效应和传输损耗。种群大小设置为100，最大迭代次数设置为500。

表1 为不同算法在系统1 上的统计结果，由表1可知，GCDE 算法和SaDE 算法在最小值、平均值、最大值和标准差方面均为最优，燃料成本均为10 094.20 美元/h，标准差均为0，可以看出GCDE 算法和SaDE 算法在系统1 上拥有最佳的优化精度。图2 为不同算法在系统1 上的收敛曲线，由图2 可以看出，GCDE 算法的收敛速度明显优于SaDE 算法，同样也优于DE 算法和DEGM 算法。结合上述分析得出，GCDE 算法在系统1 中拥有最优的优化精度与收敛速度。表2 为系统1 的各算法最优调度解。

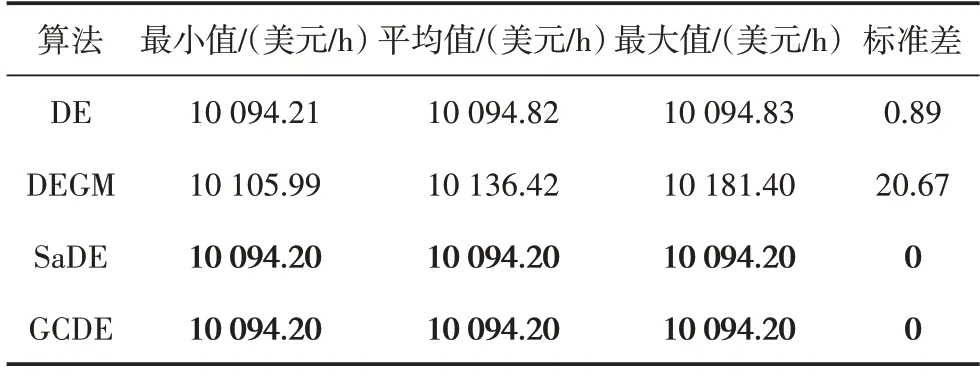
表1 系统1的统计结果Table1 Statistical results of system 1

表2 系统1的最优调度解Table 2 Optimal dispatch solution of system 1

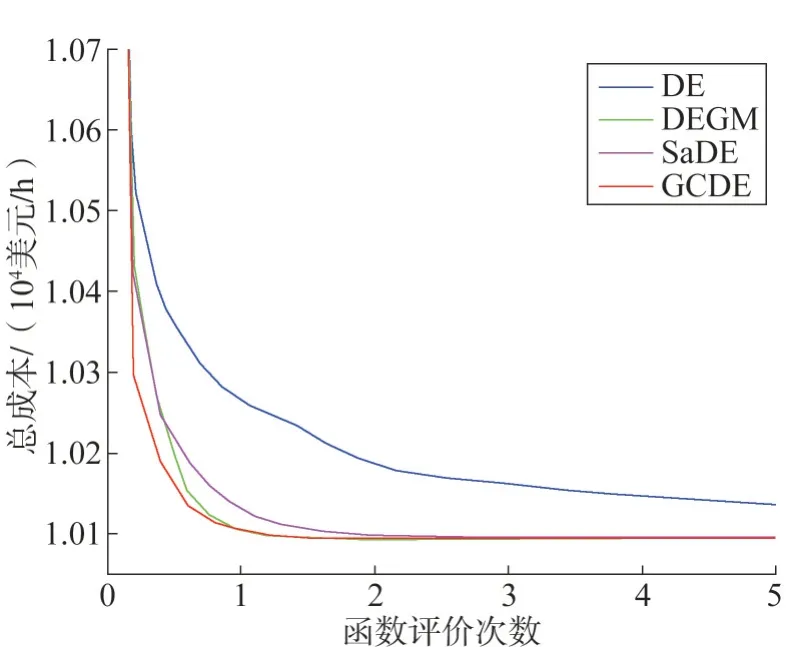
图2 系统1收敛曲线Fig.2 Convergence curve for system 1

3.2 系统2：24台机组

系统2 由13 台纯电机组、6 台热电联产机组和5台纯热机组组成。该系统的电负荷和热负荷分别为2 350 MW 和1 250 MW。该系统仅考虑阀点效应，不考虑传输损耗。种群大小设置为100，最大迭代次数设置为5 000。

表3 为不同算法在系统2 上的统计结果，由表3 可知，GCDE 算法在最小值、平均值、最大值和标准差方面均为最优，燃料成本最优为57 825.71 美元/h，标准差为6.65，可以看出GCDE 算法在系统2 上拥有良好的优化精度。图3 为不同算法在系统2 上的收敛曲线。由图3 可以看出，GCDE 算法的收敛速度明显优于其他三种算法。结合上述分析得出，GCDE算法在测试系统2 中拥有最优的优化精度与收敛速度。表4 为系统2 的各算法最优调度解。

表3 系统2的统计结果Table 3 Statistical results of system 2

表4 系统2最优调度解Table 4 Optimal dispatch solution of system 2

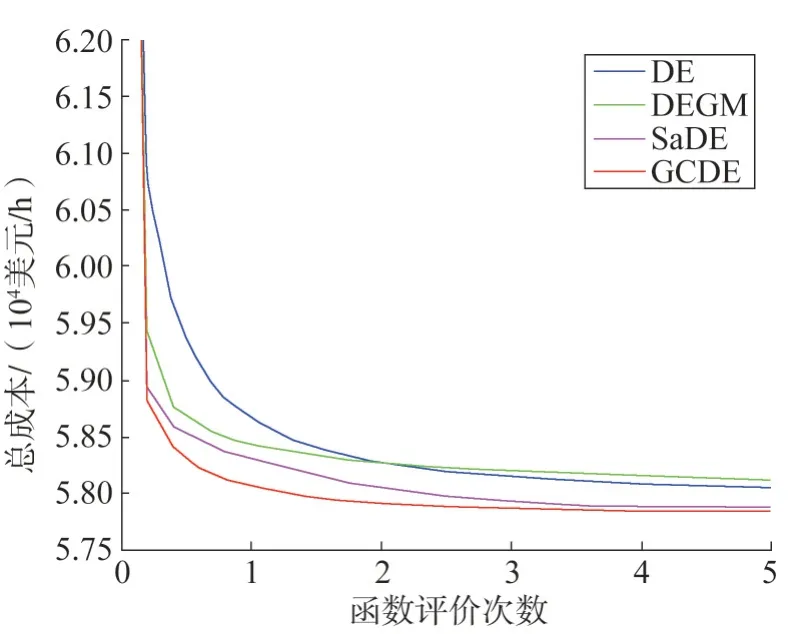
图3 系统2收敛曲线Fig.3 Convergence curve for system 2

4 结束语

针对复杂多约束CHPED 问题，提出了一种改进的高斯柯西变异自适应差分进化算法。该算法采用高斯柯西变异策略，对种群个体周围进行不同范围的局部搜索，并采用自适应参数策略调节参数，提升了算法的优化性能。结合约束修复策略，将GCDE算法应用在7 台机组和和24 台机组两种不同的CHPED 系统。仿真结果表明，GCDE 算法在这两个CHPED 系统上相比于其他三种代表差分进化算法，具有更优的求解精度和收敛速度。