基于DeCNN的逆时偏移低频噪声压制方法

万晓杰,巩向博,成 桥,于明浩

吉林大学地球探测科学与技术学院,长春 130026

0 引言

逆时偏移利用双程波动方程进行全波场逆时外推,具有成像精度高、保幅性好和无倾角限制的优点,其实现过程主要分为三部分:震源波场正向延拓;检波点波场逆时外推;选择合适的成像条件进行成像,其中以互相关成像条件[1]最为常见。在互相关成像条件下会产生非常强的成像噪声,影响成像质量,尤其是在靠近震源的相对浅层。成像噪声具有区别于有效信息的低频特性、方向特性和大角度特性[2]。低频噪声产生的主要原因有两个:应用双程波动方程产生的背向反射,以及震源波场与检波点波场波矢量夹角为超大角度时的互相关运算[3]。

根据成像噪声的成因和特性,去除逆时偏移低频噪声的方法一般可以分为3类[3]。1)在波场延拓过程中压制噪声,通过改造波动方程,使其能减弱背向反射的能量,从而达到减弱反射界面噪音的效果。Baysal等[4]提出无反射波动方程用于解决叠后逆时偏移的噪声问题。Fletcher等[5]在波动方程中加入了衰减项,即让逆时偏移噪声沿着方向衰减。2)修改成像条件来压制低频噪声。Yoon等[6]利用坡印廷(Poynting)矢量确定波传播方向,以此来进行波场分离。Chattopadhyay等[7]提出归一化互相关成像条件,在一定程度上能压制低频噪声,加强深层构造的振幅。Liu等[8]提出基于Hilbert变换的波场分离成像条件,有效去除低频噪声。3)对成像结果进行滤波去噪。此方法易于实现且计算效率高。郭念民等[2]利用高阶Laplace算子压制逆时偏移低频噪声,取得有效的成果。胡江涛等[9]提出解析时间波场外推及波场分解方法,能够在逆时偏移每个时间切片上实现波传播方向的分解。陈桂廷等[10]利用归一化照明补偿下的零延迟互相关成像条件,并对成像结果进行Laplace滤波,对Sigsbee模型有很好的成像效果。张艺山等[11]使用地震子波相位校正技术、近地表Q吸收补偿技术等确保数据质量,通过自适应全波形反演得到精确的速度模型,确保逆时偏移的成像质量。徐蔚亚等[12]实现了基于解耦延拓方程的弹性波逆时偏移方法,利用组合叠加成像策略保留大角度的成像信息,有效压制低频伪影。

近年来,随着计算机硬件和各种开源软件的发展,深度学习在地震数据重构[13]与去噪[14-15]、断层检测与识别[16-18]、地震相识别[19-20]等方面广泛应用。张昊等[21]提出用卷积神经网络(convolutional neural network, CNN)和长短期记忆(long short-term memory, LSTM)混合神经网络自动提取地震速度谱。2015年,神经网络U-Net[22]和FCN(fully convolutional network)[23]提出,二者都是卷积和反卷积的组合,这种结构的神经网络可以使地震数据或模型以类似正演和反演的方式进行训练,在地球物理中的应用非常广泛。Yang等[24]提出用FCN以多炮地震数据构建盐丘速度模型,与全波形反演(full-waveform inversion, FWI)相比取得了不错的效果。Zu等[25]应用反卷积神经网络来分离混炮数据,取得了较好的效果。Huang等[26]使用U-Net直接对稀疏的地震数据进行成像。Kong等[27]提出基于U-Net的自适应多次波去除方法。罗仁泽等[28]提出残差U型网络压制地震资料中的随机噪声。Zhong等[29]提出用U-Net去除地震数据中的随机噪声。刘霞等[30]提出了一种融合残差注意力机制的卷积神经网络,能够压制实际地震信号中的噪声。

卷积-反卷积结构的神经网络在数据去噪方面有显著成效,本文构建数据驱动的卷积-反卷积神经网络(convolution-deconvolution neural network, DeCNN)压制逆时偏移中的低频噪声,通过修改U-Net的神经网络结构和改变其卷积和反卷积操作中的激活函数来提升网络的迁移性能。以含低频噪声的震源归一化成像结果作为训练数据,以Laplace滤波结果作为标签,分别训练压制逆时偏移低频噪声的神经网络DeCNN和U-Net;用训练好的神经网络对训练数据网格大小不同模型的成像结果进行去噪处理,以验证DeCNN的迁移性能。

1 方法原理

1.1 去噪原理

逆时偏移的成像结果可以表示为

IRTM=Im+Inoise。

(1)

式中:IRTM为逆时偏移成像结果;Im为不含噪声的高精度成像结果;Inoise为低频噪声。去噪网络的目标是尽可能精确地从含低频噪声的成像结果中恢复地层反射系数。深度学习逆时偏移低频噪声压制的过程是通过对样本和标签的学习,试图建立起IRTM和Im之间的映射关系,将IRTM作为输入,输出Im,完成对低频噪声的压制工作。

1.2 神经网络理论

神经网络训练数据和标签之间的非线性映射关系,实质上是训练一个压制逆时偏移低频噪声的滤波器。训练过程可以看作最优化问题,训练合适的网络参数Θ,使目标函数收敛:

(2)

式中:N为批量标准化(batch normalization, BN)中每一批次数据的数量,BN可以解决梯度消失和梯度爆炸的问题;L(·)为损失函数,设为预测结果和标签的均方误差(mean squared error, MSE);Ii(x,z)为训练数据对应的标签。优化神经网络参数的过程可以表示为

Θi+1=Θi-λ∇L(·)。

(3)

式中,λ为步长。

目标函数的优化采用自适应矩估计(adaptive moment, Adam)算法。Adam算法相比梯度下降法有以下优点:1)可自适应地调整每个参数的学习率,使得在训练初期学习率较大,可以快速收敛,而在训练后期学习率较小,可以更精细地调整参数;2)采用动量机制,可以使训练过程更加平滑,避免参数在梯度更新中过度波动,提高训练的稳定性;3)不仅计算梯度的一阶矩估计(即梯度的均值),还计算梯度的二阶矩估计(即梯度的方差),从而更加准确地估计参数的更新方向;4)采用偏差修正,可以在训练初期更快地更新参数,避免了学习率过小的问题。Adam算法可以更快地收敛,并且更加稳定和准确地更新参数,从而提高了训练的效果和效率。

1.3 DeCNN结构

DeCNN的神经网络结构如图1a所示。本文构建的DeCNN与U-Net(图1b)相同,都包含了下采样路径和上采样路径。DeCNN删除了U-Net下采样中的一部分卷积层和最大池化层,以及上采样中的所有卷积层和跳跃连接层;DeCNN的上采样过程全部由反卷积操作完成。

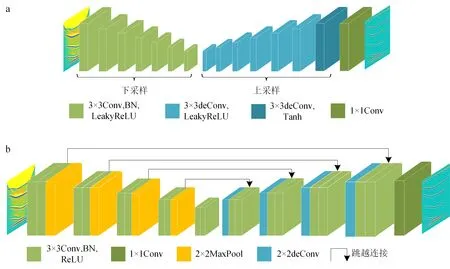
a. DeCNN;b. U-Net。Conv. 卷积; deConv. 反卷积; MaxPool. 最大池化。

卷积层对输入数据进行卷积运算,得到更高维度的特征矩阵。反卷积层并非卷积的逆过程,而是一种特殊的卷积运算,并且对卷积之后的特征图进行上采样,以便恢复图像的原始大小。

DeCNN的下采样路径包含7个模块,每一个模块都包含3×3的卷积层和BN;上采样路径也包含7个模块,每一个模块包含3×3的反卷积层和BN。与U-Net相比,除了结构的差异之外,DeCNN卷积层中采用比线性整流函数(rectified linear unit, ReLU)更加稳定的Leaky ReLU激活函数;反卷积操作中除了卷积核尺寸的不同之外,DeCNN中反卷积操作采用Tanh激活函数。两个神经网络的最后一层都为1×1的卷积操作,使网络输出恢复到和输入相同的网格大小。

非线性激活函数可以增加神经网络中的非线性因素,增强网络的泛化能力。ReLU的表达式为

f(x)=max(0,x)。

(4)

Leaky ReLU激活函数的表达式为

f(x)=max(0,x)+l·min(0,x)。

(5)

式中,l为一个较小的常数,通常取0.01。Tanh激活函数的表达式为

(6)

2 数值算例

2.1 数据准备

鉴于成像结果和数据集准备的效率方面考虑,对网格大小为 301×201 的三维SEG/EAGE(society of exploration geophysicists/ Europeanassociation of geoscientists &engineers)标准盐丘模型的1 250个切片进行10炮的逆时偏移成像,网格间距设置为dx= dz= 8 m。首先用有限差分方法正演模拟出10炮的地震记录,震源为主频f=20 Hz的雷克子波,震源位置设置在地表,检波器和震源在同一平面,共有301道,总记录时间tmax=1.6 s,时间采样间隔为1 ms。将所有单炮数据的直达波切除后作为逆时偏移反向延拓的输入数据,应用震源归一化互相关成像条件得到成像结果。

在三维盐丘的速度切片中,没有切到盐丘的速度切片为层状模型,不同位置的切片断层位置不同,层状结构也存在一定差异;不同位置处切得的盐丘模型中盐丘大小和形态各不相同。图2展示了其中4组训练数据(含低频噪声的震源归一化成像结果)和其对应标签(低频滤波结果)。可以看到:在层状模型的震源归一化成像结果(图2a、b)中,低频噪声对靠近震源位置的相对浅层影响较大,对其整体构造影响较小;在盐丘模型的震源归一化成像结果(图2e、f)中,盐丘上界面完全被低频噪声淹没,难以识别;不同模型的Laplace滤波结果对逆时偏移低频噪声有较好的压制效果(图2c、d、g、h),可以作为神经网络训练的数据标签。

a、b、e、f. 震源归一化成像结果;c、d、g、h. 对应Laplace滤波结果。

互相关成像条件的原理是只要满足波场正向外推的走时和检波点波场逆推的走时之和等于地震波传播总时间就能够成像,导致有些成像的点并不是反射界面,而只是反射路径上的某一点,并且该反射路径上的每一点都作为成像结果保留了下来,形成了强振幅的低频噪声。这些强振幅低频噪声严重模糊了成像构造(尤其在近地表处),影响了成像质量。

震源归一化互相关成像条件可表述为

(7)

式中:I(x,z)为偏移成像结果;S(x,z,t)为震源波场;R(x,z,t)为检波点波场。传统的互相关成像条件只是S(x,z,t)和R(x,z,t)的互相关,计算出的结果是无意义的量;而震源归一化成像条件可以简单理解为R(x,z,t)和S(x,z,t)的比值,能够更好地反映模型的反射系数。

2.2 神经网络训练

在神经网络训练过程中,将震源归一化成像结果作为训练数据,将低频滤波结果作为其对应标签,其中训练数据集和测试数据集的比值为8∶2。神经网络训练超参数如表1所示。

表1 网络超参数

U-Net和DeCNN的训练损失函数曲线如图3所示,两个神经网络在历元为50左右时,损失函数收敛,神经网络的训练完成。当神经网络的训练完成后,在训练好的网络中输入含低频噪声的成像结果,输出即为低频噪声压制后的结果。

图3 U-Net和DeCNN训练过程中的损失函数曲线

实验软件采用Pytorch深度学习框架,采用的服务器配置如下:英特尔E5-2620 v4处理器、Ubuntu系统、64 GB内存、GeForce RTX 3090显卡。U-Net和DeCNN训练时间分别为31和29 min,测试只需数秒时间。

2.3 神经网络测试及结果分析

神经网络训练完成后,分别用训练好的U-net和DeCNN对测试集中的层状模型和岩丘模型进行去噪处理,并与常规波场分离方法进行对比,测试神经网络的低频压制效果。层状模型的震源归一化成像结果及其Laplace滤波结果如图4所示,测试结果如图5所示。在U-Net测试结果(图5a、b)和常规波场分离方法低频压制结果(图5e、f)中,层间存在一些低频伪影(红色箭头所示),并且U-Net对层状模型中一些小散射体上方的层位信息造成一定缺失(图5a中红圈所示);而DeCNN的去噪效果较好(图5c、d)。

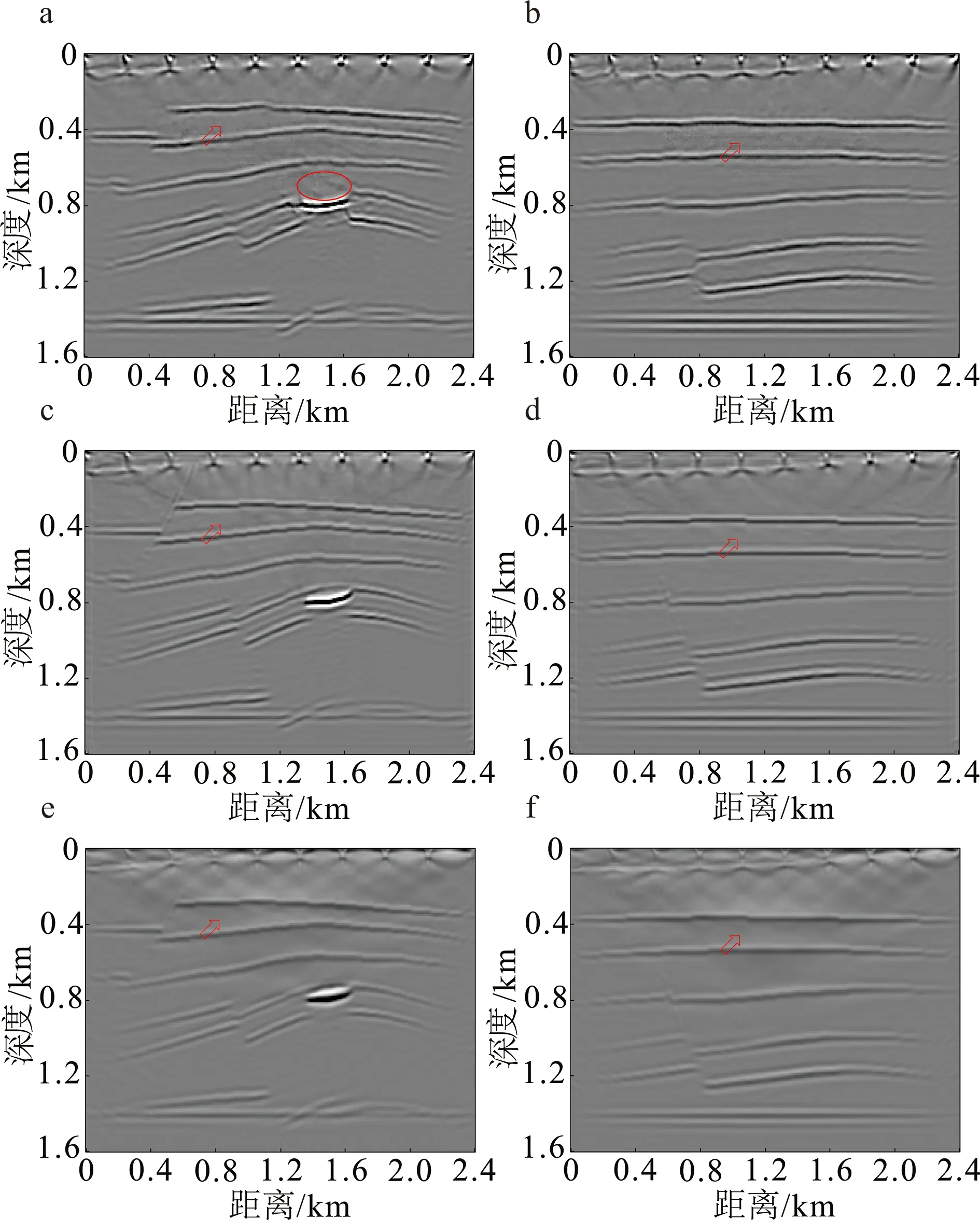
a、b. U-Net测试结果;c、d. DeCNN测试结果;e、f. 上下行波分离结果。

盐丘模型的震源归一化成像结果及其Laplace滤波结果如图6所示,测试结果如图7所示。在U-Net测试结果(图7a、b)中,盐丘上界面和盐丘上方层位信息有一定缺失(红色箭头所示);在常规波场分离方法低频压制结果(图7e、f)中,盐丘周围存在一定的低频噪声(红色箭头所示);与上述两种方法相比,DeCNN的测试结果(图7c、d)较好,没有层位缺失或者盐丘周围的低频噪声。

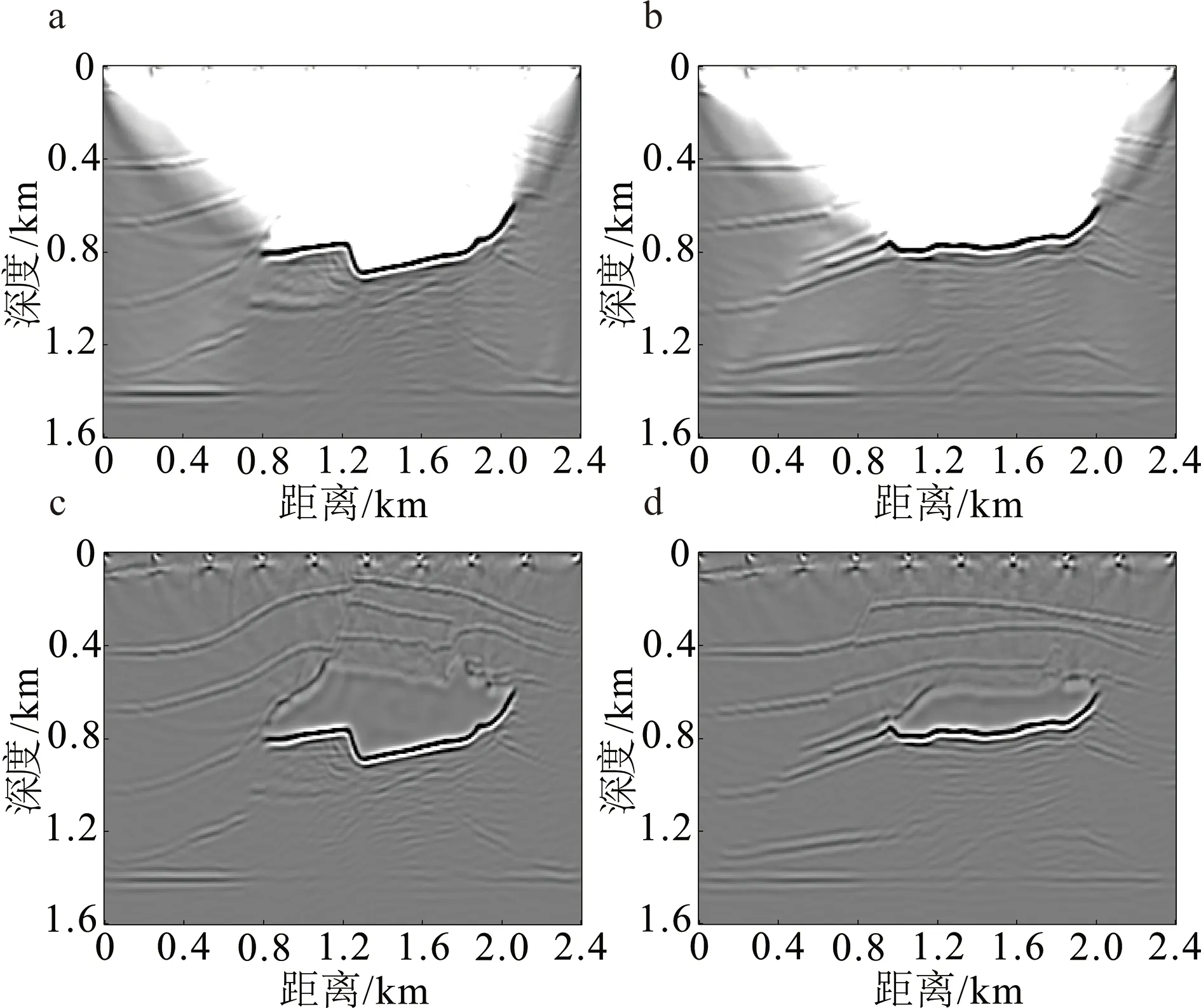
a、b. 震源归一化成像结果;c、d. 对应Laplace滤波结果。

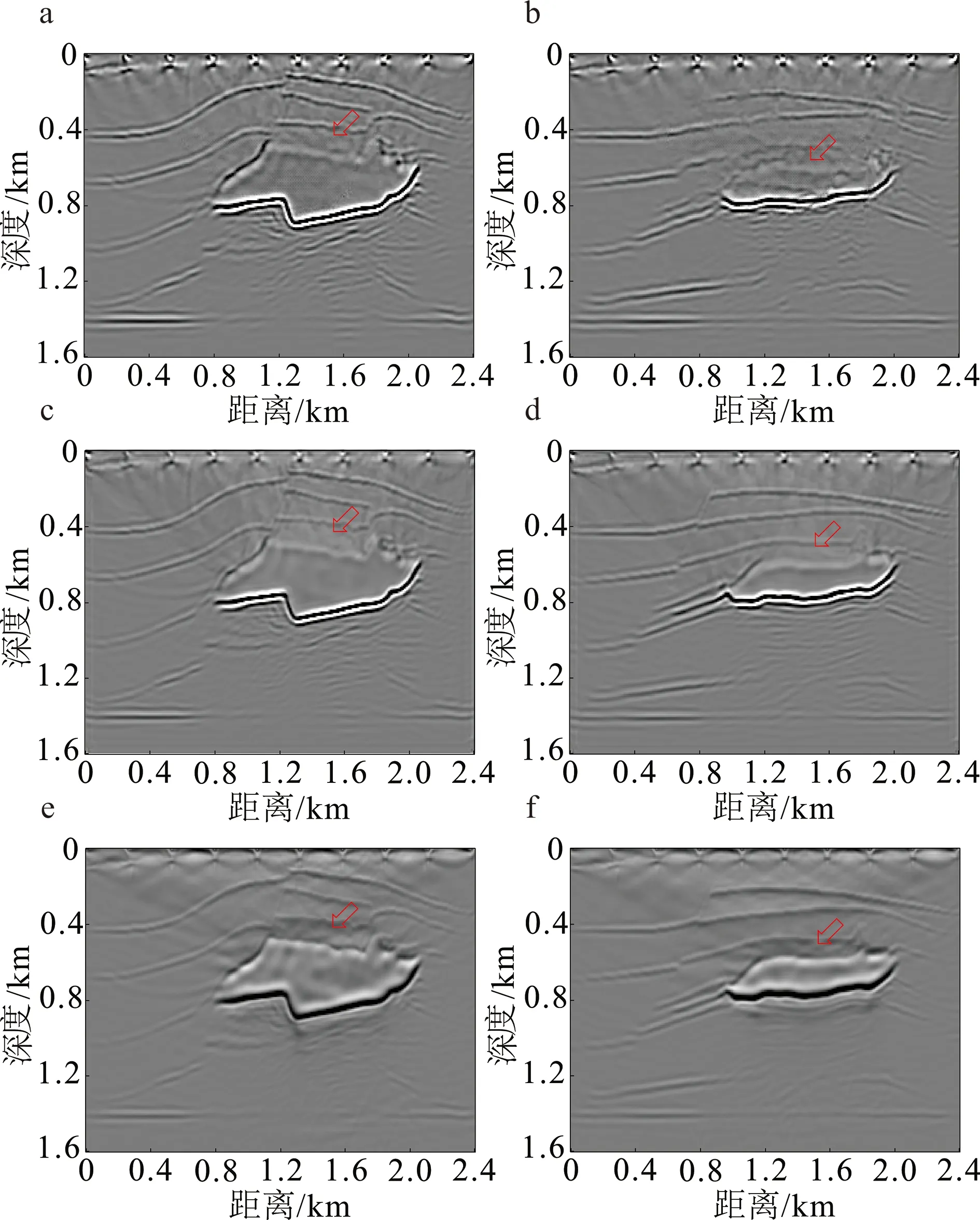
a、b. U-Net测试结果;c、d. DeCNN测试结果;e、f. 上下行波分离结果。

在单个模型的10炮偏移成像过程中,应用震源归一化成像条件,再利用Laplace滤波对成像结果进行去噪,所需时间为9 min左右;应用常规上下行波分离成像条件进行成像,所需时间大约为23 min;用训练好的神经网络对成像结果去噪,只需数秒时间,效率远高于上下行波分离成像方法。

2.4 迁移模型算例

为了验证神经网络的迁移性能,用训练好的U-net和DeCNN对与训练数据集网格大小不同的SEG/EAGE标准盐丘模型和Marmousi模型的震源归一化成像结果进行低频噪声压制,并与常规波场分离方法进行对比。迁移模型网格大小为1 000×210,其40炮的成像结果如图8、b所示。采用的网格间距dx=dz=8 m,震源为f=20 Hz的雷克子波,采样间隔为1 ms,采样时间为2 s。图8c、d分别为图8a、b的Laplace滤波结果。

a. SEG/EAGE标准盐丘模型震源归一化成像结果;b. Marmousi模型震源归一化成像结果;c. SEG/EAGE标准盐丘模型Laplace滤波结果;d. Marmousi模型Laplace滤波结果。

迁移模型测试结果如图9所示。在U-Net的测试结果(图9a、b)中,由于U-Net的分割性能[22],在与训练数据网格大小相同的位置出现分割现象(红色箭头所示);在常规波场分离方法低频压制结果(图9e、f)中,一些精细构造还存在一定的低频伪影(红色箭头所示);而DeCNN的测试结果(图9c、d)显示,DeCNN的迁移性能远远好于U-Net,其低频压制效果相比常规波场分离方法也存在一定优势。

a、b. U-Net测试结果;c、d. DeCNN测试结果;e、f. 上下行波分离结果。

表2为不同成像条件下迁移模型成像和神经网络训练、测试所需时间。可以看出,训练好的神经网络的去噪效率远高于常规上下行波分离方法。

表2 迁移模型的成像时间

3 结论

1)本文构建神经网络DeCNN压制逆时偏移低频噪声。通过模型试算,DeCNN的噪声压制效果优于U-Net,并且与常规的上下行波分离方法相比有更高的计算效率,而且其低频噪声压制效果也更好,可在一定程度上代替传统滤波方法和常规波场分离后的成像方法。

2)训练好的网络有较强的迁移性能。用训练好的神经网络对与训练数据网格大小不同的迁移模型的成像结果进行低频噪声的压制,DeCNN也能表现出较好的去噪效果,网络的迁移能力要远远好于U-Net。

3)本文从数据准备效率方面考虑,采用低频滤波结果作为标签。应用监督学习方法压制逆时偏移中的低频噪声,其结果受训练数据标签的影响较大;标签的去噪效果越好,神经网络在测试集和迁移模型中的去噪效果越好。