基于混合寻优的矿山车辆重载牵引实心轮胎模型参数辨识

任志勇 ，石 琴 ，沈 杰，武仲斌，赵 远

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009；2.中国煤炭科工集团 太原研究院有限公司,山西 太原 030006；3.安徽省智慧交通车路协同工程研究中心,安徽 合肥 230009；4.晋西工业集团有限责任公司,山西 太原 030024；5.太原理工大学 机械与运载工程学院,山西 太原 030024)

矿山车辆重载橡胶实心轮胎作为矿山车辆与地面直接接触的部件，其力学性能直接影响车辆动力学和行驶平顺特性，与常规轮胎相比，轮胎结构、材料特性以及胎路滚滑接触机理方面与常规充气轮胎模型均有一定的差别，具有橡胶实心、阻尼低、花纹粗大、扁平率大等特点。因而，采用传统方法中的充气轮胎模型及经验参数对矿山车辆进行动力学建模及仿真计算时，很可能产生较大的模型失配误差，也就无法准确描述矿山重载车辆的实际运动状态，并对其行为进行精准调控，成为长期制约矿山车辆动力学和稳定性研究的关键难题，始终未得到根本解决。因此，考虑到胎路接触力学特性对车辆横向稳定性能调控的重要影响[1-4]，研究矿山车辆重载牵引橡胶实心轮胎在水泥路面上的非线性滚滑接触力学特性，针对性地根据轮胎材料、几何结构特征等对重载橡胶实心轮胎模型参数进行准确辨识，建立适用于矿山典型路面环境和重载运输车辆轮胎力的求解模型显得尤为重要。

当前国外学者如 VETTURI D 等[5]设计了适用于轮胎参数辨识的通用遗传算法程序。MANTARAS 等[6]使用多体动力学软件 ADAMS 对虚拟模型进行动态仿真，集成遗传算法对轮胎路面摩擦因数得到了相关模型参数。ORTIZ A 和 CABRERA J A 等[7]将差分进化(DE，Differential Evolution)算法与基因算法的变异算子结合，提出新的优化算法(IMMA)来确定轮胎魔术公式参数。CABRERA J A 等[8]提出协同进化算法MUCA(Co-evolutionary Approach)，分成2 个阶段完成魔术公式轮胎参数辨识。TALEBITOOTI R 等[9]采用遗传算法(全局搜索，得到初始值)+LM 算法(梯度算法)对轮胎魔术公式参数进行辨识。ALAGAPPAN 等[10]对比了信赖域反射法、Nelder-Mead 单纯形法、Pattern search、差分、粒子群搜索、布谷鸟搜索6 种辨识方法。

国内学者张云清等[11]结合数值优化算法和遗传算法优点，利用 MATLAB 优化工具箱完成辨识。边伟等[12]采用遗传算法来辨识轮胎魔术公式参数，采用MATLAB 遗传算法工具箱先辨识出一级参数，再基于一级参数利用遗传算法辨识二级参数。张丽霞等[13]加入自适应权重和自然选择性的粒子群算法，并将PAC89 轮胎模型参数分为两级进行辨识。程泽木等[14]根据最小二乘原理，基于六分力的测试数据，将下山单纯形法(Nelder-Mead)、遗传算法与随机值法相结合，形成一种混合优化算法进行轮胎模型参数辨识。王前等[15]提出一种新的自适应差分进化方法(New Self-Adaptive Differential Evolution，NSADE)，完成纯侧偏工况侧向力和回正力矩参数的辨识。

笔者借鉴文献[16-17]选用最新版本的PAC2002魔术公式模型作为基础模型，基于矿山车辆轮胎特有的桥或轮边减速器与轮胎刚性连接、铰接转向等工况特点，通过修正相关参数建立了矿山车辆重载牵引实心轮胎纯纵滑工况下纵向力和侧偏-纵滑复合工况下纵向力的数学模型，同时针对矿山车辆轮胎垂向载荷范围大所导致的强非线性特点，传统算法参数设置与寻优策略难以适应的问题，基于高斯牛顿迭代法、遗传算法和模拟退火算法各自的特点，提出了一种矿山车辆重载牵引实心轮胎模型混合寻优辨识算法。通过六分力测试设备获取相关试验数据，分别对纯纵滑及侧偏-纵滑复合2 种工况下的轮胎模型参数进行辨识，并与单纯的遗传算法在算法性能上进行对比分析，同时采用整车牵引特性试验验证辨识模型的准确性。

1 重载牵引实心轮胎模型数学建模

1.1 重载牵引实心轮胎模型坐标系的定义

重载牵引实心轮胎模型采用印迹坐标系，本文采用ISO 轮胎坐标系，如图1 所示(图1 中，V为轮胎滚动的速度；w为坐标系标识)。

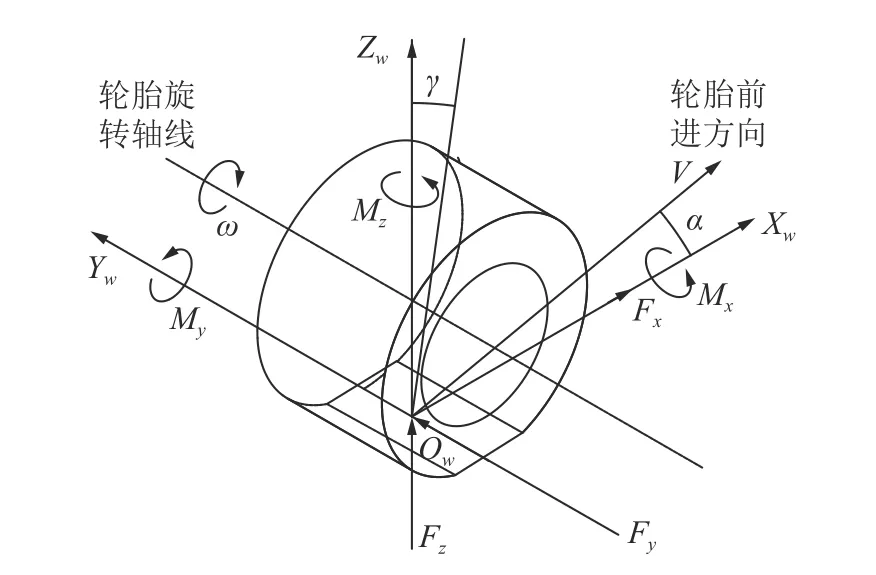
图1 重载牵引实心轮胎ISO 坐标系Fig.1 Heavy traction solid tire ISO coordinate system

坐标系原点Ow定义在轮胎接地印迹中心，OwXw轴为车轮平面与地平面的交线，前进方向为正，即轮胎滚动的方向，反之为负。OwZw轴垂直于地面，向上方向为正，反之为负；OwYw由右手定则确定，为轮胎旋转轴线在地面上的投影线，向左为正，反之为负。同时定义轮胎中心运动方向与轮胎回转平面的夹角定义为轮胎侧偏角α，从上往下看，逆时针为正，反之为负；γ为外倾角，从前进方向看，顺时针为正，逆时针为负；同时定义矿用重载牵引实心轮胎的六分力及平面内外特性，见表1。

表1 重载牵引实心轮胎六分力定义及特性Table 1 Definition and characteristics of six component force of heavy traction solid tire

1.2 重载牵引实心轮胎模型

鉴于当前轮胎模型研究主要分为经验模型、理论模型和半经验模型，但经验模型很难适用于多种测试工况和测试条件，理论模型存在公式复杂、计算繁琐、精度较差等问题。本文研究矿山车辆重载牵引实心轮胎时，选用业界广泛认可的半经验模型，其兼容了经验模型和理论模型的优点，半经验模型最具代表性的是魔术公式(Magic Formula，MF)轮胎模型。

笔者采用最新版本的魔术公式轮胎模型PAC2002 模型，是PACEJKA 等[18]不断更新和完善的一种广泛应用于车辆动力学仿真和分析的MF 模型。鉴于矿山车辆牵引特性是衡量矿山设备可靠性与适应能力的重要标准，具有非常实际的应用价值和迫切的研究需求，故本文只研究适用于该类车辆重载牵引实心轮胎的牵引特性，重点关注纯纵滑工况下纵向力Fx和侧偏-纵滑复合工况下纵向力Fxk。

基于重载牵引实心轮胎自身橡胶实心、刚性连接和无外倾等特点，研究时忽略PAC2002 轮胎模型基本公式中最大侧偏刚性和侧偏摩擦因数随气压变化的4 个参数，均默认为0，且定义缩放系数均为1，则修正后的纯纵滑工况下纵向力计算公式为

式中，Fwz为轮胎垂向载荷；Fwz0为轮胎标称垂向载荷；dfwz为归一化垂向载荷增量；λ为滑移率；λx为修正滑移率；Cx、Dx、Ex、Kx、Bx为纵滑工况纵向力计算因子；SVx、SHx分别为曲线垂向和横向漂移量，可根据轮胎试验数据拟合得到。

由式(1)可知，修正后的重载牵引实心轮胎在纯纵滑工况下纵向力计算公式中待辨识的特征参数共计15 个，见表2。

表2 重载牵引实心轮胎纯纵滑工况纵向力待辨识的参数Table 2 Parameters to be identified for longitudinal force of heavy traction solid tire under pure longitudinal sliding condition

修正后的侧偏-纵滑复合工况下纵向力计算公式为

式中，αs为修正侧偏角；Cxk、Dxk、Exk、Bxk为复合工况纵向力计算因子；SHxk为曲线横向漂移量，可根据轮胎试验数据拟合得到；M为公式代号，是为了简化公式长度。

由式(3)可知，修正后的重载牵引实心轮胎在侧偏-纵滑复合工况下纵向力计算公式待辨识参数是在纯侧偏工况的基础上增加了6 个，共计21 个，见表3。

表3 重载牵引实心轮胎侧偏-纵滑复合工况纵向力待辨识的参数Table 3 Parameters to be identified for longitudinal force of heavy traction solid tire under complex operating conditions of cornering and longitudinal-slip

2 混合寻优算法

2.1 建立优化模型及评价指标的建立

定义参数辨识优化模型为

式中，Z（x）为目标函数，即辨识误差；FMF(xi)为拟合数据；FTEST(xi)为试验数据；n为试验组数；xi为待辨识参数。

其物理意义为将识别得到的参数代入到轮胎模型中，相同条件下计算结果与实际测试数值差值的平方根最小，对应的解最优，即希望较小目标函数值对应解的适应度值较高。

为了进一步研究轮胎模型辨识效果，引入相对均方根误差(Root Mean Square Error，ERMS)和确定系数(Rs)作为辨识精度评价指标。

其物理意义为ERMS越小代表辨识精度越高，Rs表征曲线数据拟合的好坏，正常取值范围为[0,1]，越接近1，表明数据拟合的越好。

2.2 混合寻优算法的设计

矿山车辆重载牵引实心轮胎模型具有参数多和高度非线性的特点，最佳的辨识算法要求有较高的计算效率和计算速度。高斯牛顿迭代法具有计算量较低，计算较快特点，但稳定性很差，算法可能不收敛；遗传算法具有较好的并行搜索能力，但其爬山能力弱，收敛特性较差，容易产生早熟，算法易陷入局部最优特点；模拟退火算法具有较好的局部搜索性能，且有较好的收敛性，但算法全局捜索能力不强。

笔者基于上述3 种算法各自的特点，设计了一种混合寻优算法，首先利用高斯牛顿算法将待辨识函数泰勒展开，忽略二阶及二阶以上的偏导数项，迭代得到初次辨识参数。通过遗传算法和模拟退火算法对初次辨识参数进行深度寻优，每代种群中最优解用模拟退火算法进行再次搜索，增强算法的搜索能力，并通过模拟退火算法保持种群的多样性，避免种群收敛于某一局部区域[21]。具体的算法步骤如图2 所示（图2 中，为残差平方和；为迭代残差平方和；T0为初始温度，T=T0，Tk为迭代第k次时的温度；T为算法中的温度；w为辨识状态 ；w0为辨识初始状态；k为迭代次数 ；Δf为迭代的误差；Δf2为重新取值迭代的误差；f(wi)为按照新状态wi求解的函数值；f(wi2)为按照新状态wi2重新求解的函数值；f(w02)为按照新状态取值求解的函数值；i，j分别为遗传种群里2 个个体）。

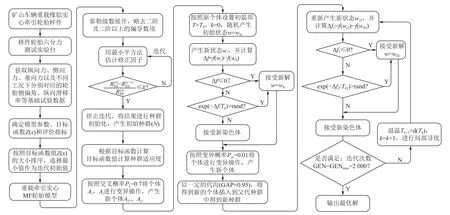
图2 混合寻优算法参数辨识流程Fig.2 Parameter identification process of hybrid optimization algorithm

2.3 轮胎数据选择及算法参数初始化

结合矿山车辆重载牵引实心轮胎实际应用工况，侧偏角α分别取值为±10°、±9°、±8°、±7°、±6°、±5°、±4°、±3°、±2°、±1°、0°，合计21 组数据；轮胎垂向载荷Fwz分别按照20、30、40、50 和60 kN 进行取值，共计5 组数据，外倾角γ的取值为0°。

算法中控制参数分别设置为：初始化种群数N=100，代沟GAP=0.95，变异概率Pm=0.01，交叉概率Pc=0.7，最大迭代次数GENmax=2 000，规定误差率k=10-3。

利用MATLAB 软件编程对参数进行辨识，按照混合寻优算法和遗传算法2 种方法进行参数识别[19-20]。

3 轮胎模型参数识别

3.1 基础数据获取

依据矿山车辆重载牵引实心轮胎动力学原理，进行不同垂向载荷下的轮胎六分力测试试验，试验对象选用中国煤炭科工集团太原研究院有限公司生产的某型号25 t 蓄电池分布式驱动铲板式支架搬运车轮胎，轮胎类型为聚氨酯橡胶实心轮胎，型号为56×33，轮胎直径为1 100 mm，轮胎宽度为550 mm，最大接地比压为1.56 MPa，载质量25 t 车速12 km/h 时最大承载为40 t，试验路面选用水泥路面，运行速度5 km/h，侧偏角为-10°～+10°，滑转率为-0.8～+0.8，轮胎六分力测试试验如图3 所示。

图3 橡胶实心轮胎六分力测试试验Fig.3 Six component force test of solid rubber tire

3.2 纯纵滑工况纵向力参数辨识

采用混合寻优算法和遗传算法分别对纯纵滑工况下纵向力数学模型中的15 个待辨识参数进行辨识。图4 为2 种算法10 组力参数识别目标函数值变化曲线。

图4 纯纵滑工况下2 种算法的10 组纵向力参数识别目标函数值变化曲线对比Fig.4 Comparison of target function value change curves for 10 groups of longitudinal force parameters identified by two algorithms under pure longitudinal slip condition

根据图4 以及记录的算法时间和通过式(5)、(6)计算得到2 种算法性能评价指标见表4。

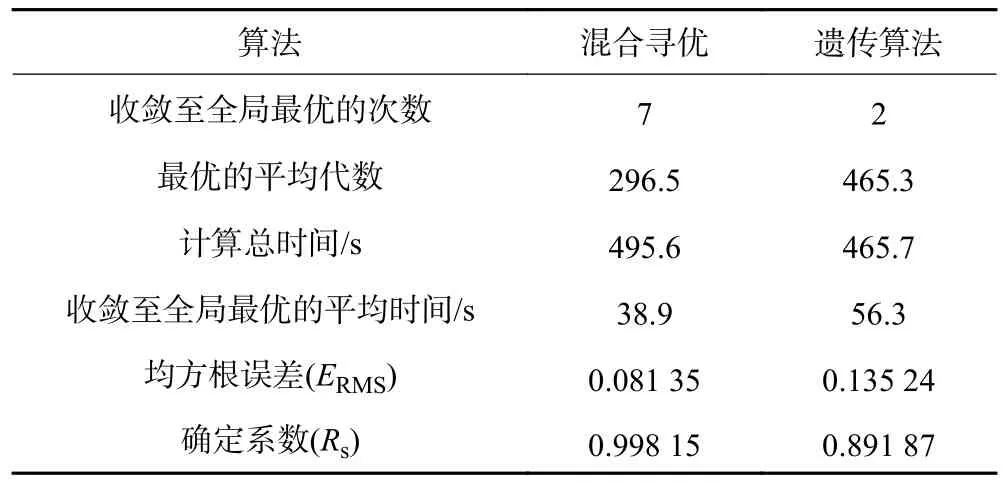
表4 纯纵滑工况下2 种算法纵向力辨识性能比较Table 4 Comparison of identification performance of two algorithms for longitudinal force under pure longitudinal slip condition

由表4 可知，混合寻优算法在矿山车辆重载牵引实心轮胎模型纯纵滑工况下纵向力参数辨识全局寻优及快速收敛能力上较遗传算法有较大的提高，收敛至全局最优的成功率达到70%，较遗传算法增加了50%，收敛至全局最优的平均代数上减小了36%，收敛至全局最优的总时间增加了6%，收敛至全局最优的平均时间减小了31%；纯纵滑工况下轮胎纵向力辨识目标函数的均方根误差(ERMS)和确定系数(Rs)分别为0.081 35 和0.999 145，2 项评价指标较单一遗传算法分别提升了66%和12%。

通过混合寻优算法进行纯纵滑工况下纵向力参数计算，识别出纯纵滑工况下重载牵引实心轮胎最佳侧向力参数见表5。

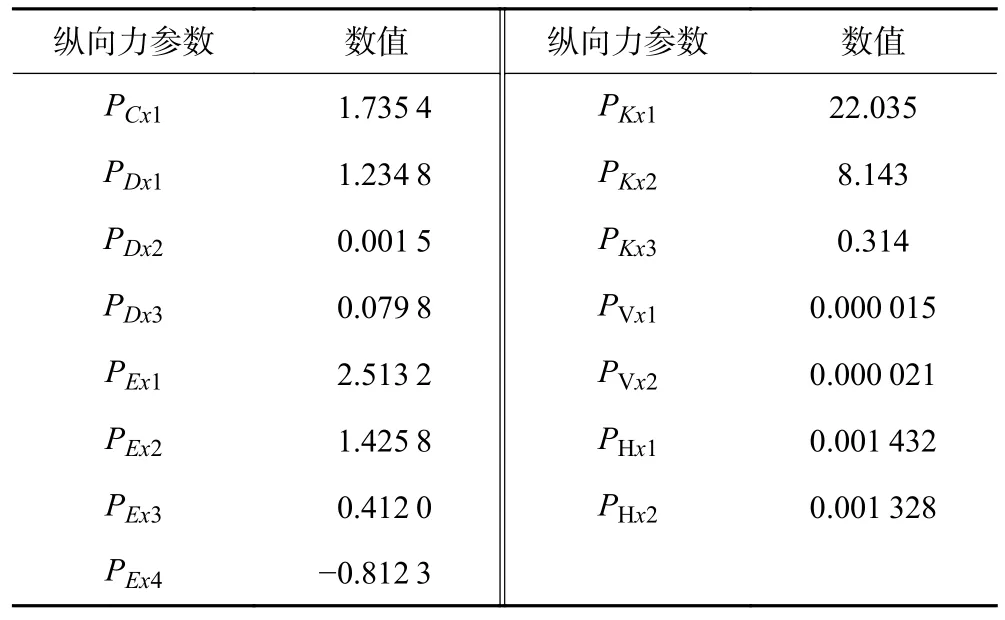
表5 纯纵滑工况的最佳纵向力参数辨识结果Table 5 Identification results of optimal longitudinal force parameters under pure longitudinal slip condition

使用混合寻优算法辨识出纯纵滑工况下，不同垂直载荷时的轮胎纵向力辨识结果和试验结果对比曲线，如图5 所示。

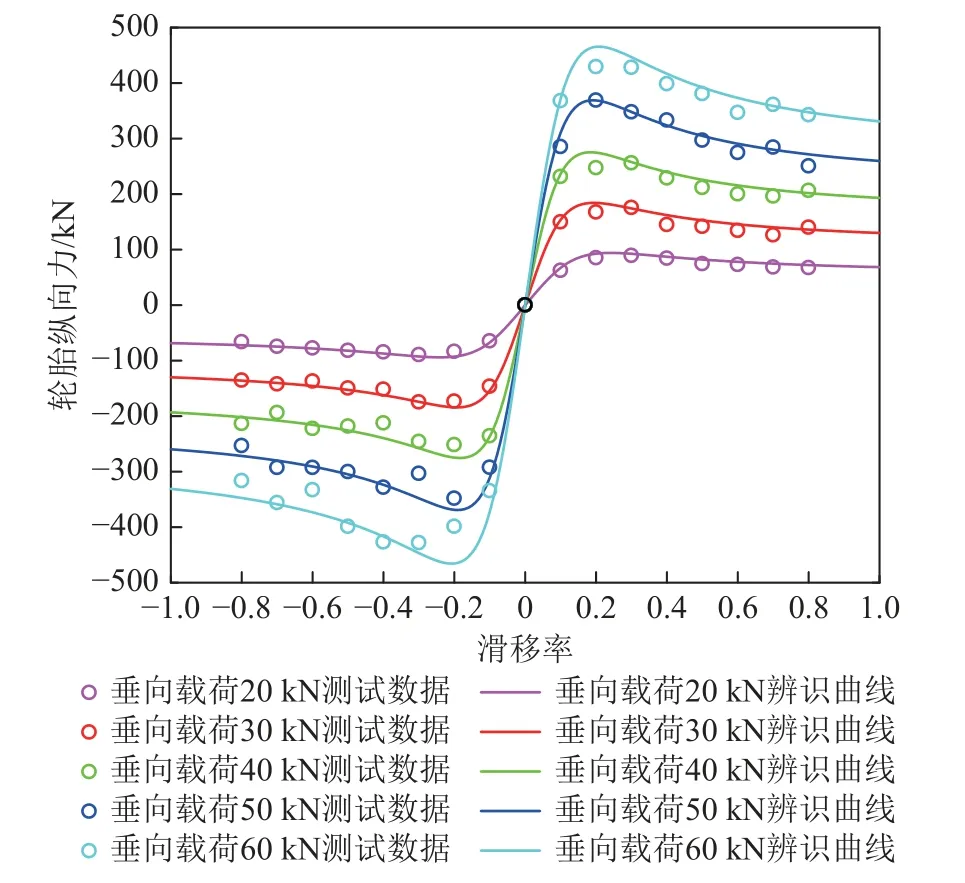
图5 纯纵滑工况下纵向力曲线Fig.5 Longitudinal force curves of cornering and longitudinalslip under pure longitudinal slip condition

结合表4 中均方根误差(ERMS)和确定系数(Rs)，由图5 可知，使用混合优化算法得到的纯纵滑工况下纵向力曲线与测试数据重合度较高，辨识结果也较精确。

3.3 侧偏-纵滑复合工况纵向力参数辨识

采用混合优化算法和遗传算法分别对侧偏-纵滑复合工况下轮胎侧向力数学模型中的21 个参数进行辨识。图6 为2 种算法10 组纵向力参数识别目标函数值变化曲线。

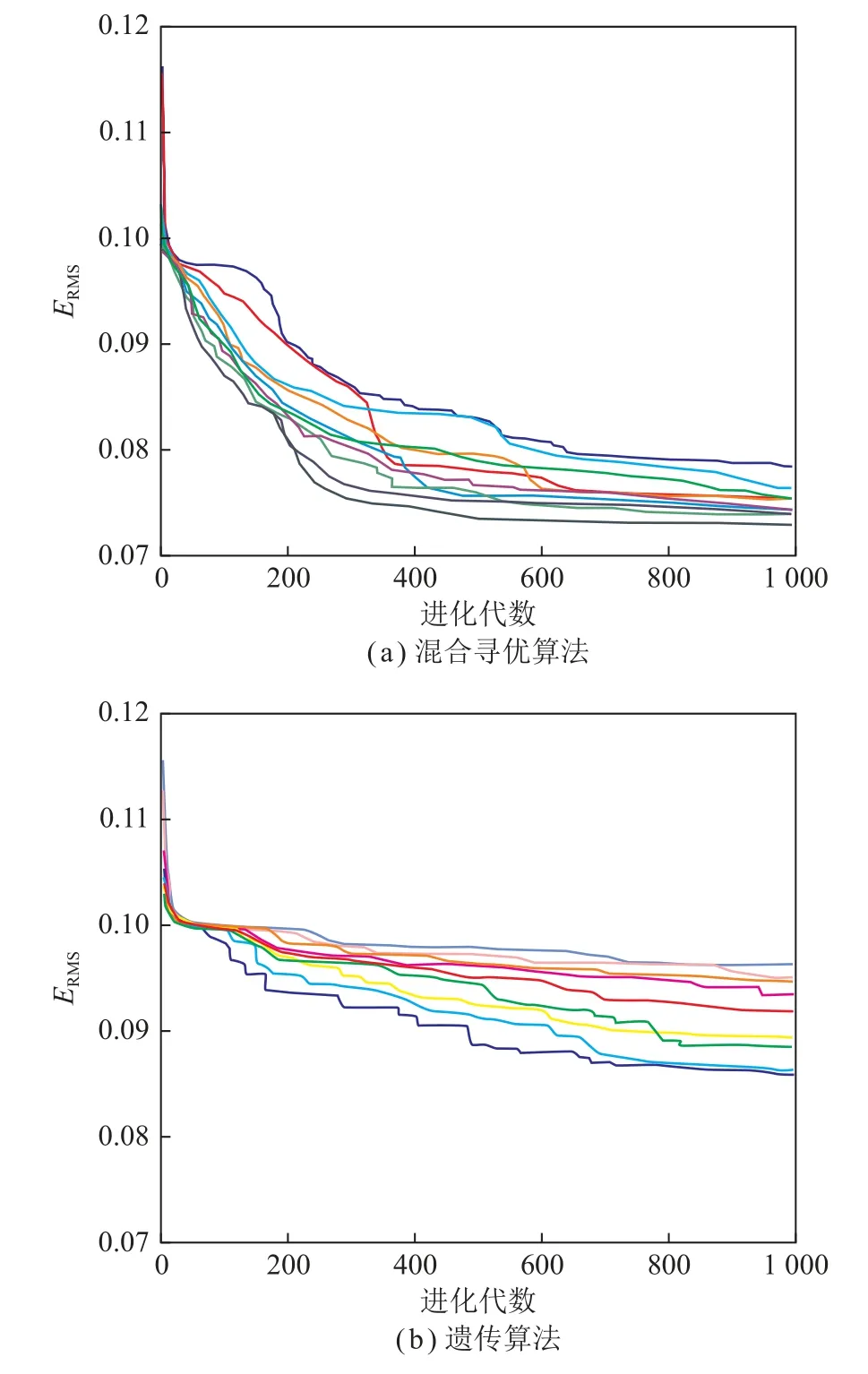
图6 复合工况下2 种算法的10 组纵向力参数识别目标函数值变化曲线对比Fig.6 Comparison of 10 groups of longitudinal force parameter identification target function value change curves of two algorithms under complex operating conditions

根据图6 以及记录的算法时间和通过式(5)和(6)计算得到2 种算法性能的评价指标，见表6。

表6 复合工况下2 种算法纵向力辨识性能比较Table 6 Comparison of identification performance of two algorithms for longitudinal force under complex operating conditions

由表6 可知，混合寻优算法在矿山车辆重载牵引实心轮胎模型复合工况下纵向力参数辨识全局寻优及快速收敛能力上较遗传算法有较大的提高，收敛至全局最优的成功率达到60%，较遗传算法增加了40%，收敛至全局最优的平均代数上减小了13%，收敛至全局最优的总时间增加了1.6%，收敛至全局最优的平均时间减小了39%；侧偏-纵滑复合工况下纵向力辨识目标函数的均方根误差(ERMS)和确定系数(Rs)分别为0.079 65 和0.987 65，2 项评价指标较单一遗传算法分别提升了31%和13%。

通过混合寻优算法侧偏-纵滑复合工况下纵向力参数计算，识别出重载牵引实心轮胎侧偏-纵滑复合工况下最佳纵向力参数见表7。

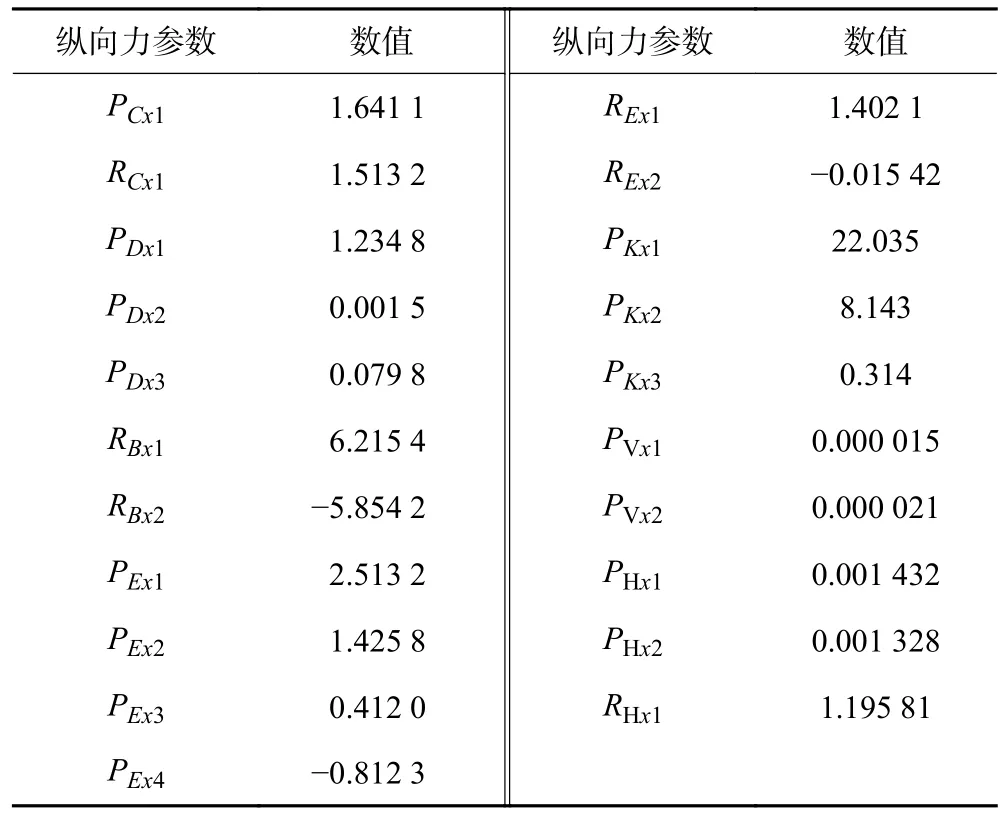
表7 复合工况最佳纵向力参数辨识结果Table 7 Identification results of optimum longitudinal force parameters under complex operating conditions

使用混合寻优算法得到侧偏-纵滑复合工况下不同滑移率时的轮胎纵向力辨识结果与试验数据对比曲线，如图7 所示。

图7 侧偏-纵滑复合工况下纵向力曲线Fig.7 Longitudinal force curves under complex operating conditions of cornering and longitudinal-slip

结合表6 中均方根误差(ERMS)和确定系数(Rs)计算值，由图7 可知，使用混合优化算法得到的侧偏-纵滑复合工况下不同纵向滑移率时的纵向力曲线与测试数据具有较高的重合度，辨识结果也较精确。

4 牵引特性实验验证

为了验证混合寻优算法对矿山车辆重载牵引实心轮胎模型参数辨识的准确性，本文进行整车牵引特性试验验证，实验样机仍然选用中国煤炭科工集团太原研究院有限公司生产的某型号25 t 分布式驱动铲板式支架搬运车。

基于MATLAB/Simulink 数值仿真环境，建立典型矿山车辆整车12-DOF 动力学模型、实心轮胎模型、驾驶员模型、分布式轮边驱动控制模型以及折腰控制模型。同时在Adams/View 环境中建立支架搬运车虚拟样机动力学仿真模型，通过与Simulink 控制模型的联合仿真，将辨识的最佳参数代入到轮胎模型中，求解出矿山车辆轮胎牵引特性，联合仿真模型如图8 所示。

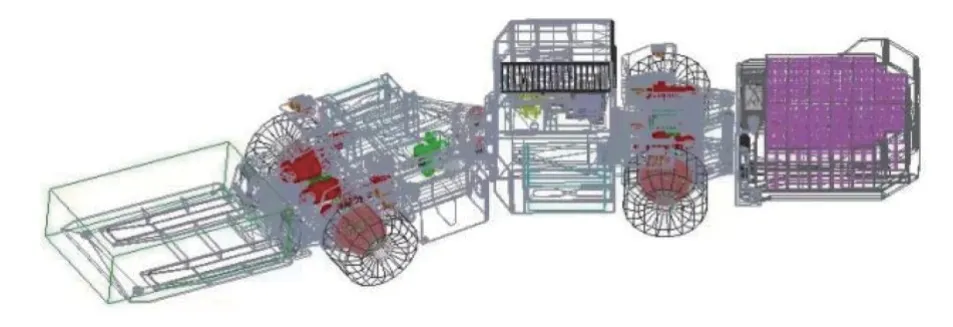
图8 矿山车辆联合仿真模型Fig.8 Co-simulation model of mine vehicles

实验时为了确保整车验证数据的一致性，轮胎垂直载荷大小按照实车实际测试数据进行选择，即在试验样机铲板处装载不同加载试验样块，等效至某一个轮胎垂向载荷的数值，试验如图9 所示。

图9 橡胶实心轮胎垂直载荷试验Fig.9 Vertical load test of rubber solid tire

受现场实验条件限制，试验时选取0、5、10、15和20 t 五组不同的质量，等效至各轮胎的垂直载荷数据见表8。

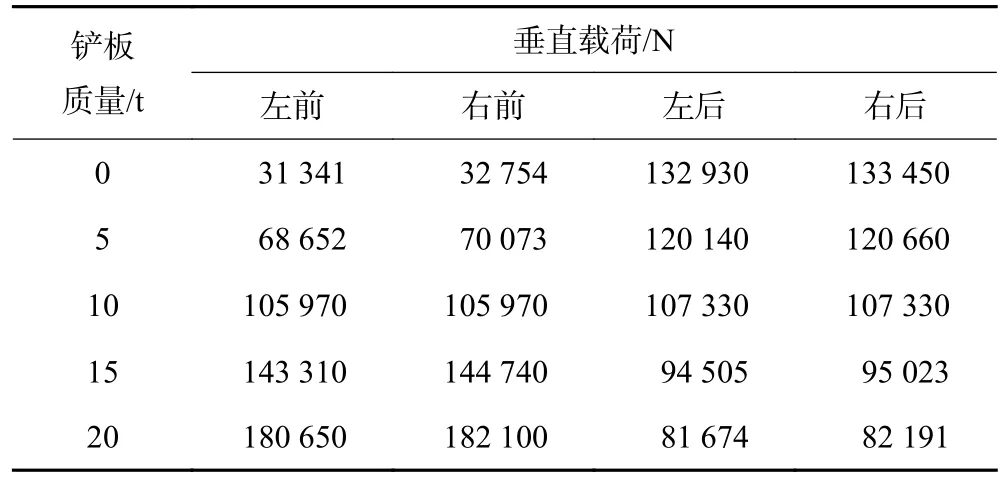
表8 橡胶实心轮胎垂直载荷实验数据Table 8 Vertical load test data of solid rubber tire

鉴于滑移率测试实验条件，选择左前轮胎作为实验对象，同时选用了分别直线行驶时水平、12°和14°水泥干硬路面3 组数据进行验证。实验时，通过软件控制，将后驱动轮驱动转矩置0，而将总驱动转矩平均分配至左前轮和右前轮，因此，后轮变为纯滚动的从动轮，而前轮仍为滚滑共存的驱动轮，车辆速度可通过纯滚动的后轮转速估计得到，滑转率则可以通过前轮进行计算。试验现场照片如图10 所示。

鉴于研究对象采用分布式轮边电机驱动，每一台驱动电机装机前均进行了台架标定，输出转矩可以精确获得，且驱动电机与轮胎刚性连接，不存在外倾，实验时通过整车控制器读取轮边驱动电机转速等效为整车车轮的滚动角速度ω。

整车车速测试时，在车辆尾部纵向中心处安装了速度测试装置，装置上安装压紧弹簧确保滚动轮与地面充分接触，滚动轮采用变形较小的硬质橡胶，确保滚动半径不变，滚动轮轴端安装有旋转编码器实时采集角速度，并通过RS485 通讯方式传递至整车控制器，计算求得车辆实时行驶速度u。车轮半径r采用静态时测量数值进行等效；通过式(7)计算出对应的滑移率：

将参数辨识结果代入到对应的纵向力数学模型中，进一步计算轮胎的牵引特性，以此验证辨识模型的有效性，验证时按照承载不同的垂向载荷进行验证，不同垂向载荷下的轮胎牵引力随滑移率λ变化计算结果和测试结果对比如图11 所示。

由图11 可知，依据辨识参数计算得到的单个轮胎纵向牵引力与实车实验结果之间的偏差不超过4%，验证了辨识模型的有效性。

5 结论

(1)本文提出的混合寻优算法辨识结果与试验值均方根误差(ERMS)最大为0.081 35，确定系数(Rs)均超过了0.98。

（2）魔术公式轮胎模型是基于试验数据的经验轮胎模型，轮胎六分力测试试验设备能够排除次要因素模拟出特定的轮胎行驶条件，准确地再现轮胎的各种工作情况。纯纵滑及侧偏-纵滑复合现象是煤矿重型车辆作业现场最为常见的2 种工况，遗传算法对于强非线性轮胎模型参数辨识时较难收敛，尤其在复合工况下迭代次数增多，陷入局部寻优循环。

（3）全局寻优混合寻优算法在矿山车辆重载牵引实心轮胎模型参数辨识全局寻优及快速收敛能力上较遗传算法有较大的提高。而且通过实验验证，依据辨识参数计算得到的轮胎纵向牵引力与实车实验结果之间的偏差不超过4%，也充分验证了辨识模型的有效性。