适应未知环境的模糊阻抗控制方法

沈逸超，卢 岩，姚逸辉，庄春刚

（上海交通大学机械与动力工程学院，上海 200240）

1 引言

当下绝大多数的机器人是基于位置控制的，从规定的位置出发经过预设轨迹到达期望的位置。这类机器人可以应用于搬运、点焊和喷漆等不需要控制机器人与环境间接触力的工业场景。但当机器人进行与环境间存在接触力的作业时，机器人位置控制则因为无法完成对加工过程中力的控制而不能满足工艺需求了［1］，此时需要引入机器人阻抗控制。但是传统的定参数阻抗控制框架无法适应多变复杂的加工工况［2］。如何实现阻抗控制参数随加工工况［3］变化的实时调整成为了这里的研究重点。采用将模糊逻辑控制器与阻抗控制器相结合的方法［4］，使阻抗控制参数能随实际加工工况而变化［5］，从而实现变阻抗控制［6］。在Simulink中完成了基于阻抗控制的机器人力控框架的搭建，并进行了阻抗控制参数对机器人位置/接触力响应曲线的影响的研究［7］。

2 阻抗控制

2.1 阻抗控制原理

阻抗控制是将机器人力/位控制系统设计成一个质量m-阻尼b-弹簧k系统，通过改变阻抗控制器的惯性参数、阻尼参数和刚度参数来实现对机器人与环境间的接触力和位置关系的调节［8］。

E表示期望接触力Fd与实际接触力F之间的偏差，即：

2.2 基于位置的机器人阻抗控制

当机器人末端执行器与环境接触时，执行器的运动将会受到环境约束，那么在研究机器人末端执行器力/位置控制时，应该将机器人与环境结合起来考虑，当认为环境刚度为固定值时，机器人与环境间的作用力形式上满足胡克定律。此时可以用弹簧模型来表示机器人与环境间的作用力变化规律，如式（3）所示。

式中：ke—外界环境刚度；Xe—接触位置。

当机器人所处的位置X≤Xe时，代表机器人与环境刚好接触或不接触，则机器人与环境间的作用力为0，当机器人所处的位置X＞Xe时，代表机器人与环境已经接触并产生了接触力。

末端执行器位置修正量与接触力偏差eF在频域上存在以下关系：

2.3 阻抗控制误差分析

在磨削、抛光和去毛刺等机器人末端执行器与环境相接触的作业中，对期望接触力的跟踪效果将直接影响该工序的加工效果。基于位置的机器人阻抗控制具有实现简单、鲁棒性强和无需精确动力学模型的特点。

本节选取机器人对平面进行磨削这个实际场景为物理模型［9］，进行后续分析与推导。机器人对平面进行磨削时接触力的控制，可以简化为机器人末端执行器在Z方向上的力/位置控制问题。

由式（1）、式（3）可知：

可求得：

3 模糊阻抗控制

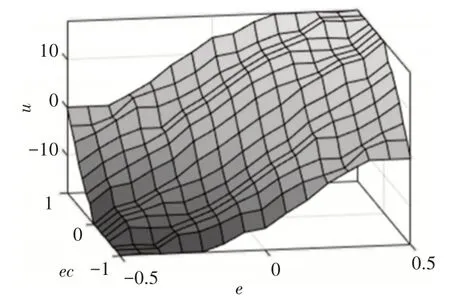
图1 模糊控制规则Fig.1 Fuzzy Control Rules

基于上述研究内容，选择好合适的阻抗控制参数将改善阻抗控制中对期望力和期望轨迹的跟踪效果，但传统的定参数阻抗控制框架无法适应多变复杂的加工工况。采用将模糊逻辑控制器与阻抗控制器相结合的方法实现变阻抗控制［9］。首先需要确定模糊控制器输入量与输出量的个数，然后对输入量与输出量进行细分。｛NB、NM、NS、Z0、PS、PM、PB｝。这里选取高斯隶属度函数。完成输入输出量的细分和隶属度函数的确定后，即可完成模糊化与清晰化过程。

基于阻抗控制的机器人力控算法和已经设计好的模糊控制器，将两者结合起来则得到了基于模糊阻抗控制的机器人力控算法，如图2所示。模糊控制器以力误差ΔF与力误差的导数作为输入量，输出量为机器人阻抗控制参数m、b、k的动态调整值Δm、Δb、Δk，阻抗控制参数的动态调整值与阻抗控制参数的初始值相加则可得到变阻抗控制的实际值。模糊控制器与阻抗控制器共同构成了机器人的模糊阻抗控制器［10］。

图2 基于模糊阻抗控制的力控算法Fig.2 Force Control Algorithm Based on Fuzzy Impedance Control

3.1 基于模糊阻抗控制的恒力跟踪设计

在Simulink 中依照图2的力控算法搭建仿真框架。给出机器人期望的运动轨迹是在z=0.4m的平面进行圆周运动，此时假设环境刚度为500N/m，机器人与环境间期望的接触力为22N，机器人与环境开始接触的位置为z=0.43m。机器人PI位置控制器中的参数为：P=5、I=0.1。机器人的关节力矩控制器采用了计算力矩控制方法。

3.2 基于模糊阻抗控制的变力跟踪设计

在机器人实际加工的过程中，由于加工工件材质可能存在的不均匀现象，加工过程中的力热耦合，机器人加工过程中的期望接触力可能不是恒力，而是一个时变量，所以有必要对机器人阻抗控制进行变力跟踪的仿真，以研究机器人阻抗控制的变力跟踪性能。

在Simulink 的仿真框架中将期望接触力修改为Fd=22+4 sin πt。

3.3 基于模糊阻抗控制的变刚度环境下的恒力跟踪设计

在机器人实际加工的过程中，由于与机器人相接触的外部环境的刚度往往是变化的，所以有必要对机器人阻抗控制进行变刚度环境下的恒力跟踪仿真。

要进行变刚度环境下的恒力跟踪的仿真，只需要在仿真框架中将环境刚度修改为ke=500+10 sint。

4 算法实现

md、bd、kd分别代表着惯性参数、阻尼参数和刚度参数。在实际生产加工中，这三个参数均是人为给定的，不随时变。在仿真过程中取md=1、bd=150、kd=30。

机器人从初始状态过渡到稳态，使用puma560沿给定期望轨迹做圆周运动的过程，如图3所示。

图3 过渡仿真过程Fig.3 Simulation Process

4.1 模糊阻抗控制的恒力跟踪仿真

基于模糊阻抗控制的力控算法能有效减少系统的超调量，降低实际接触力峰值约2.7N，系统达到稳态的时间由2s 缩短至0.7s，体现了模糊阻抗控制性能相较于定参数阻抗控制的性能优越性，如图4所示。端轨迹图，如图5所示。一条线为期望z=0.4时的轨迹，一条线为模糊阻抗控制轨迹，另一条线为定参数阻抗控制的轨迹。

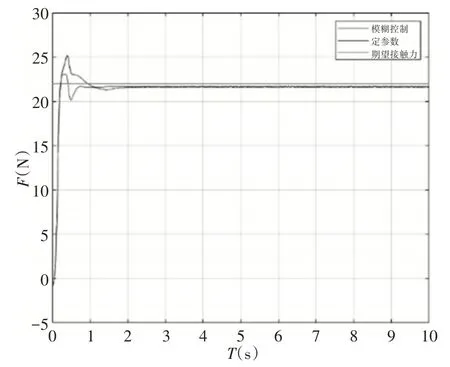
图4 恒力跟踪对比Fig.4 Constant Force Tracking

图5 末端轨迹图Fig.5 End-Effector Trajectory

4.2 模糊阻抗控制的变力跟踪仿真

基于模糊阻抗控制的力控算法能有效实现变力跟踪，而定参数阻抗控制的机器人力控算法在对变力的跟踪上则存在着较大的滞后，如图6所示。体现了模糊阻抗控制对时变性控制问题的良好性能。末端轨迹图，如图7所示。一条线为期望z=0.4时的轨迹，一条线为模糊阻抗控制轨迹，另一条线为定参数阻抗控制的轨迹。

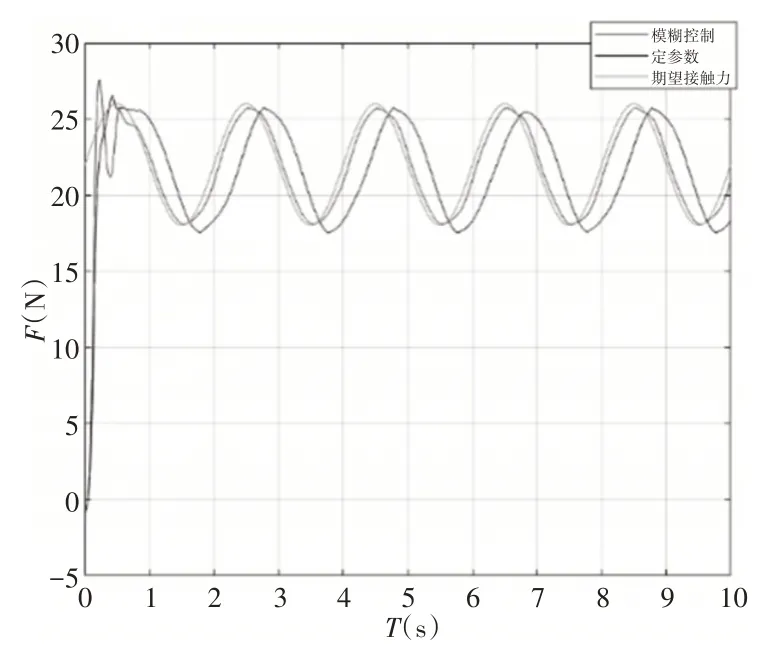
图6 变力跟踪对比Fig.6 Variable Force Tracking

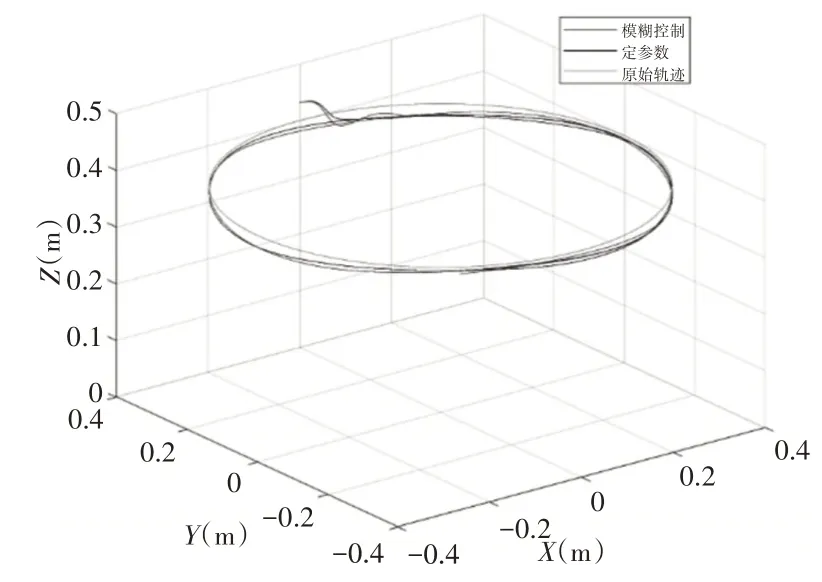
图7 末端轨迹图Fig.7 End-Effector Trajectory

4.3 模糊阻抗控制变刚度环境下恒力跟踪仿真

基于模糊阻抗控制的力控算法能有效实现变刚度环境下的恒力跟踪，而定参数阻抗控制的机器人力控算法在变刚度环境下则存在着较大的超调量和较大的稳态误差，如图8 所示。体现了模糊阻抗控制在变刚度环境下相较于定参数阻抗控制的良好性能。末端轨迹图，如图9所示。一条线为期望z=0.4时的轨迹，一条线为模糊阻抗控制轨迹，另一条线为定参数阻抗控制的轨迹。

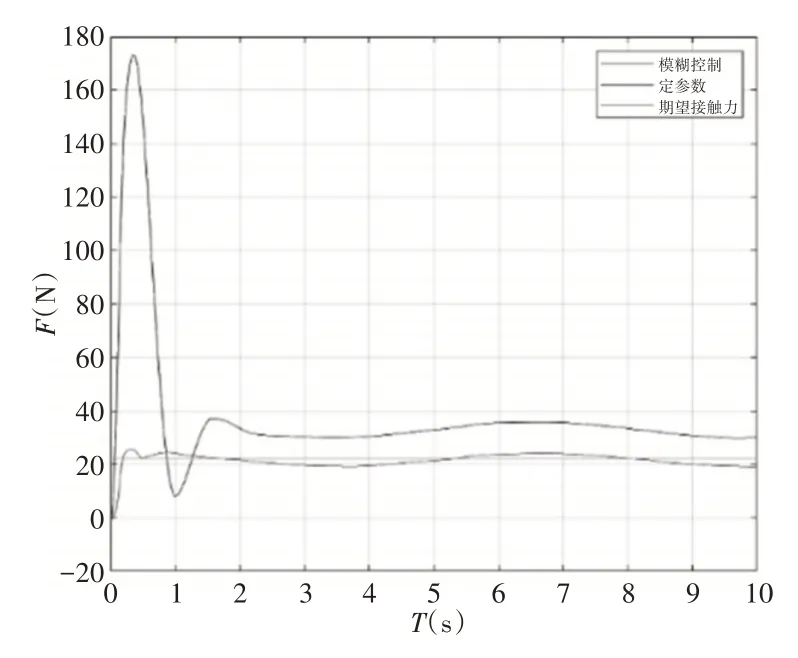
图8 变刚度环境下的恒力跟踪对比Fig.8 Constant Force Tracking on Alterable Stiffness Environment

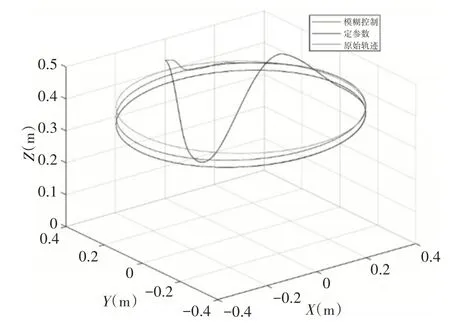
图9 末端轨迹图Fig.9 End-Effector Trajectory

这里将模糊控制应用在阻抗控制上完成了基于模糊阻抗控制的机器人力控框架的搭建，通过仿真进行了3种情况下基于模糊阻抗控制与定参数阻抗控制的力控算法对比，验证了机器人模糊阻抗控制的性能优越性。

5 结论

采用阻抗控制方法针对工业机器人在接触类作业中位置/接触力的控制进行研究。在传统的阻抗控制框架上，引入模糊逻辑控制器对阻抗控制参数进行实时优化，使机器人控制系统能针对外界环境的变化，及时调整控制参数，最终实现力柔顺功能。尽管机器人位置与环境的接触力/控制研究由于其复杂性和成本限制，实现工业落地的还比较少，当下只有少部分协作机器人具备了力柔顺功能，但随着制造业对智能化的要求越来越高，具有力柔顺功能的机器人被大规模应用的场景是未来可期的。