机械臂轨迹的非支配排序高斯粒子群多目标优化

刘 祎

（宿迁学院机电工程学院，江苏 宿迁 223800）

1 引言

机械臂不仅可以代替人类进行强度大、重复性高、危险性高的生产活动，而且其工作效率、使用成本也远远优于人力。机械臂轨迹规划是机械臂控制技术的核心内容之一，轨迹的优劣极大地影响其运行性能和使用寿命［1］。因此研究机械臂轨迹规划具有重要价值。

按照规划空间的不同，机械臂轨迹规划可以分为关节空间和笛卡尔空间2类。关节空间轨迹规划是指确定关节角与时间的函数［2］，其优点是可以直接用于电机控制量设计，缺点是难以使末端执行器跟踪设定轨迹。笛卡尔空间轨迹规划是确定末端执行器的位姿与时间的函数［3］，其优点是规划效果直观明了，缺点是需转化到关节空间才能进行控制，转化过程计算量较大，且容易出现奇异性和机械自锁问题。这里研究的是关节空间轨迹规划问题，根据不同的规划要求，关节空间轨迹规划分为针对给定路径的规划和点到点间规划。针对给定路径的规划，是根据给定的末端路径规划出各关节轨迹；点到点间规划，是指给定若干个必经点规划出各关节轨迹［4］，这种机械臂一般在无障碍物环境下运行，比如垛码、装配机器人等。根据优化目标的不同，一般将机械臂轨迹规划分为时间最少优化、能耗最低优化、冲击最小优化等，文献［5］研究了深海用机械臂的最小能耗优化方法，使用径向基神经网络构建了机械臂能耗模型，使用自适应粒子群算法求解了优化模型，有效降低了机械臂能耗。文献［6］提出了4-3-3-3-4的分段多项式轨迹，分别使用粒子群算法和差分进化算法进行时间最优轨迹规划，粒子群算法优化的各关节更平滑且时间最优。文献［7］针对机械臂的振动和磨损问题，采用5次非均匀B样条函数构造插值曲线，并使用NSGA-II算法进行优化，使机械臂运行过程中的冲击较小。当前关于路径规划的研究，大都更加关注时间最优而忽略其他性能，对时间、能耗和冲击的综合优化才更加合理。另外，算法的优化性能也能够影响路径规划的优劣。

这里针对机械臂关节空间轨迹的优化问题，设计了笛卡尔空间必经点，以5次多项式为轨迹基元用于规划点与点间的轨迹。以达到各必经点时间为优化对象，建立了多目标优化函数，提出了非支配排序高斯粒子群算法的优化方法，实现了运行时间、能耗和冲击的多方面优化。

2 问题描述与建模

2.1 问题描述

这里以PUMA560机械臂为研究对象，如图1所示。该机械臂具有6个转动关节，前3个转动关节用于控制末端执行器的位置，后3个关节用于控制末端执行器的姿态，这里针对末端执行器的位置进行研究和优化，因此只与前3个关节角相关。

图1 PUMA560机械臂Fig.1 PUMA560 Manipulator

根据任务需求，设置PUMA560机械臂末端执行器必须经过的3点在笛卡尔空间分布，如图2所示。图中点与点之间的轨迹为机械臂的现行运行轨迹，现行轨迹点与点间运行时间均为2s。这里研究内容为：在保证末端执行器经过必经点前提下，对机械臂运行轨迹进行优化。

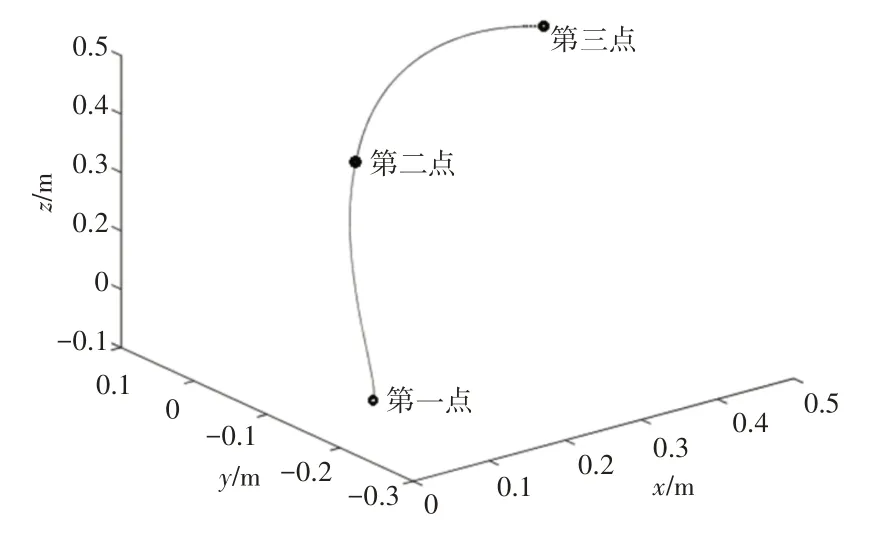
图2 给定的轨迹点Fig.2 Given Trajectory Points

使用逆运动学求解方法，基于PUMA560的D-H 模型参数，得到3个笛卡尔空间点对应的关节空间点，如表1所示。

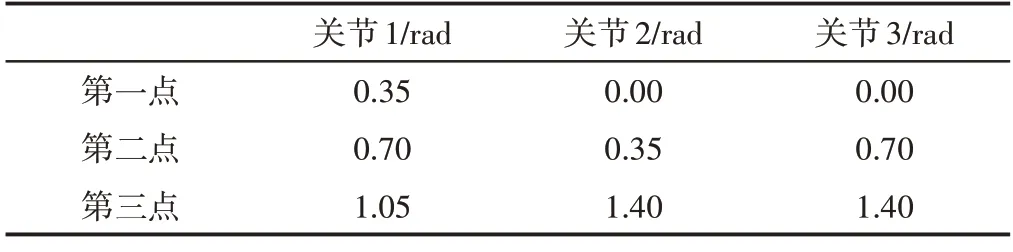
表1 相应的关节空间位置Tab.1 Corresponding Joint Space Positions

这里所研究问题描述为：对于给定的3个位置点，点与点之间使用5次多项式作为轨迹基元，第一点为初始位置，初始位置对应的时刻为初始时刻，记为t0。通过对机械臂末端到达第二点和第三点的时刻t1、t2进行优化，达到减小运行时间、节省能量消耗等目的。第三点为末端位置，末端位置对应的时刻为终止时刻，记为tf，这里的tf=t2

2.2 轨迹基元

这里使用5次多项式作为点与点间的插值轨迹，也即轨迹基元。即关节n的关节角θn随时间t的变化函数为［8］：

式中：a0～a5—第0次项系数到第5次项系数。

将该段轨迹初始时刻和终止时刻的位置、速度、加速度等作为约束条件，可以对式（1）进行求解，也即可以确定点与点之间的轨迹。初始时刻和终止时刻关节角分别记为θ0和θf，初始速度记为v0，终止速度记为vf，初始加速度记为α0，终止加速度记为αf。则得到轨迹基元待定参数为：

将式（2）得到的系数代入到式（1）中，即可得到点与点之间的运行轨迹。

2.3 问题建模

这里对机械臂轨迹规划设定3个优化目标，分别为运行时间最短、能量消耗最低、脉动冲击最小。

（1）运行时间最短。根据2.1 节的问题描述，机械臂运行时间为：

式中：T—机械臂的运行时间；y1—时间优化目标函数。

（2）能量消耗最低。机械臂驱动电机的能耗模型为：

式中：y2—能耗优化目标函数；n—关节角编号；αn(t)—关节角n随时间变化的加速度函数。

（3）脉动冲击最小。机械臂在运行过程中的脉动冲击计算方法为：

式中：y3—脉动冲击优化目标函数；

Jn(t)—关节角n随时间变化的加加速度函数。

机械臂轨迹在优化过程中，应在关节运动能力的约束范围内，关节的运动能力约束包括转动角范围、角速度约束、角加速度约束、角加加速度约束，则多目标优化模型为：

式中：θn_max—关节n的角度极值；Vn_max—关节n的速度极值；αn_max—关节角n的加速度极值；Jn_max—关节角n的加加速度极值。PUMA560机械臂的运动能力约束，如表2所示。

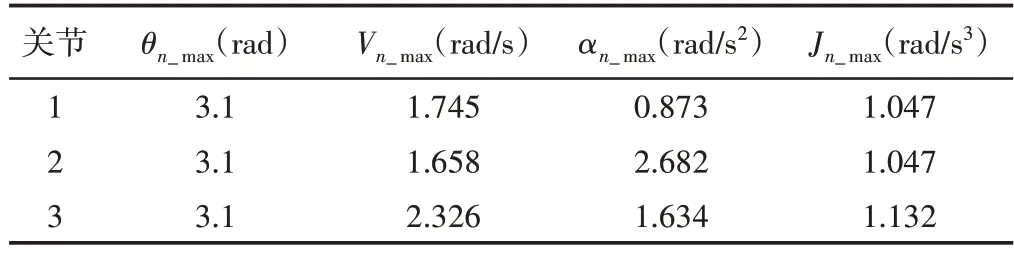
表2 PUMA560活动能力约束Tab.2 Mobility Constraint of PUMA560

3 多目标优化模型求解

对于多目标优化问题，一般具有2种处理方法：（1）使用加权系数法，将多个优化目标转化为一个目标；（2）使用非支配排序法，得到多个优化目标的Pareto解集。第1种方法可以视为第2种情况下的一个特殊解，因此这里在非支配排序的基础上，提出了基于非支配排序粒子群算法的多目标优化方法。

3.1 基于非支配排序的多目标优化选择方法

多目标优化的选择过程是基于非支配排序和拥挤度实现的。非支配排序是针对多目标优化问题提出的排序方法，与传统排序方法相比，它使用多个评价指标，个体具有某一指标的绝对优势就说明此个体可取［9］。具体的讲，对于L个最小化优化问题，若对于任意一个目标l∈{1，2，…L}都有fl(xA)≤fl(xB)，则称个体A支配个体B。在种群中若某一个体不被其余任意个体支配，则此个体称为非支配个体。非支配排序过程为：首先选择种群中的非支配个体作为第1层，去除第1层个体后，其余个体中的非支配个体作为第2层，不断重复以上过程，直至排序完毕。

拥挤度因子是针对各层个体的聚集程度定义的，每一层两端的个体拥挤度定义为无穷大，其余个体的拥挤度大小为：

则多目标优化的选择方法为：将更新前后的个体进行混合并分层，首先保留非支配层较小的个体，当选择到某一支配层个体种群规模超出时，使用拥挤度因子进行选择，保留最后一层拥挤度因子较大的个体，直至种群规模维持不变。

3.2 基于高斯粒子群的个体更新

传统粒子群算法中，粒子依据种群信息、个体经验和自身惯性进行运动，给出粒子更新方法并进行缺陷分析［10］，为：

分析式（8）可知，随着迭代的进行，所有粒子在引导作用下向种群最优聚集，当某一粒子与种群最优相似度较大，此时有由此可以看出，当某一粒子与种群最优接近时，粒子只在自身惯性作用下更新，自身经验和种群信息将失去牵引作用，粒子群算法几乎丧失了更新能力。为了解决这一问题，一般使用随机产生粒子的方式，但是随机产生粒子后，新生粒子适应度难以超过种群最优，在式（8）作用下又会再次陷入上述问题。因此，这里提出向种群最优的邻域学习，而不是单纯的向种群最优学习。具体方法为：向种群最优施加高斯扰动，得到其邻域，使用种群最优的邻域对其余粒子进行引导，即：

高斯扰动的幅度依据算法需要进行设置，算法前期种群最优的学习价值较小，且粒子需要大范围搜索，因此使用较大的标准差；算法后期种群最优的学习价值较大，且算法具有收敛的需求，因此使用较小的标准差。基于以上分析，这里将标准差设置为递减函数，为：

式中：σ0—初始标准差，为常值；

Kmax—最大迭代次数。

3.3 高斯粒子群与粒子群算法对比

传统粒子群算法与高斯粒子群算法的粒子速度均由3部分组成，分别为自身惯性、自身经验和种群信息，以上3种影响因素分别用矢量u→1、u→2和u→3来代替，则传统粒子群算法和高斯粒子群算法的粒子更新和多样性对比，如图3所示。粒子群算法向固定的种群最优学习，而高斯粒子群算法是向种群最优的邻域学习，高斯粒子群算法的学习范围更广，既保留了高效的精英学习方式，同时增加了粒子多样性，由此可以看出，高斯粒子群算法优化深度和优化能力好于传统的粒子群算法。

图3 两种粒子群算法速度更新区域Fig.3 Speed Update Area of the Two PSO

3.4 非支配排序高斯粒子群算法流程

根据优化目标和优化参数，将粒子位置设置为2 维，即x=(t1，t2)。基于非支配排序高斯粒子群算法的多目标优化流程为：

（1）初始化算法参数，包括粒子规模、最大迭代次数Kmax、自身学习因子c1、种群学习因子c2、运动惯性w、初始标准差σ0；初始化粒子位置；（2）粒子按照式（9）和式（10）定义的方式进行位置更新；（3）将位置更新前后的粒子进行混合，并依据各目标函数值进行非支配排序并选择；（4）k=k+1，判断k=Kmax？若否则返回（3）；若否则算法结束，输出Pareto前沿解。

4 仿真验证与分析

4.1 优化结果

在3.3节从原理上对比了高斯粒子群与传统粒子群算法的优劣，也即从原理上保证了高斯粒子群算法的优越性，因此不再对2种算法的优化性能进行验证，而直接使用高斯粒子群算法进行求解。设置机械臂的边界条件为：速度v0=vf=0，加速度α0=αf=0。算法参数设置为：粒子规模为100、最大迭代次数Kmax=200、自身学习因子c1=1.50、种群学习因子c2=1.50、运动惯性w=0.6、初始标准差σ0=0.1 · range，range 表示优化维度的取值范围。使用非支配排序高斯粒子群算法得到的Pareto前沿解，如图4所示。对图4给出的优化结果作以下说明：（1）图中给出的优化结果只是各关节针对自身目标、必经点和约束得到的优化结果，机械臂联动时，点与点间运行时间按照各关节运行时间最大值进行确定；（2）Pareto前沿解集给出了不同方案下的优化结果，设计者可以按照优化需求选择优化方案。由图3优化结果可以看出，3个优化目标中，脉动量与能耗成正相关关系，但是脉动量和能耗与实践成负相关，具有一定的制约关系。

图4 优化结果Fig.4 Optimizing Result

4.2 优化前后对比与分析

按照3个优化目标同等重要选择一组优化结果，即对3个优化目标权值均设置为1/3。得到此时的3个关节优化结果分别为［1.5017，1.9315］，［1.7016，1.9914］，［1.6016，1.9832］。各关节点之间按照运行时间最大值进行确定，得到整个机械臂的运行结果为［1.7016，1.9914］。

前文中提到，图2所示轨迹为现行轨迹，将优化后轨迹与现行轨迹进行对比结果，如图5～图7所示。

图5 关节1优化前后对比Fig.5 Comparison of Joint1 Before and After Optimization

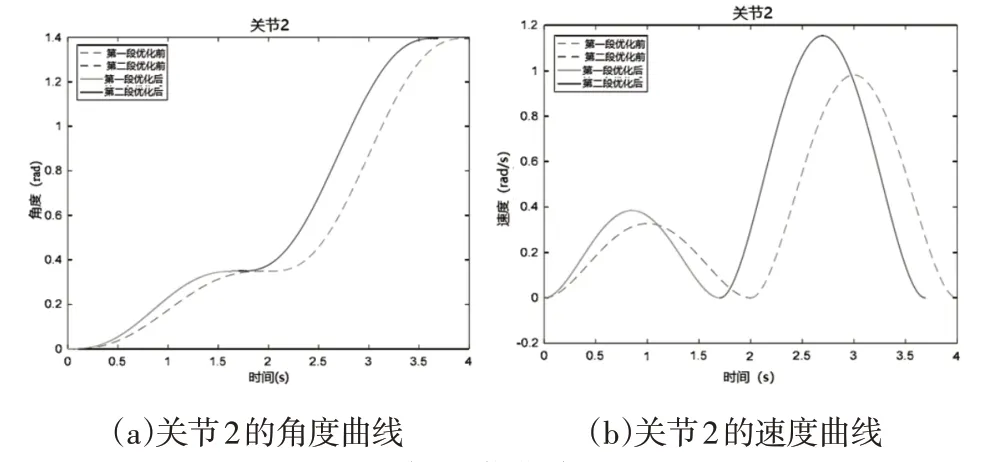
图6 关节2优化前后对比Fig.6 Comparison of Joint2 Before and After Optimization

图7 关节3优化前后对比Fig.7 Comparison of Joint3 Before and After Optimization

由图5～图7可以直观看出，经过优化机械臂的运行时间明显减少，关节角速度幅值比优化前略大，但是由于优化后的运行时间短，因此能耗仍需进一步计算才能比较，无法直观看出。统计优化前后的运行时间、能耗和冲击量，如表3所示。

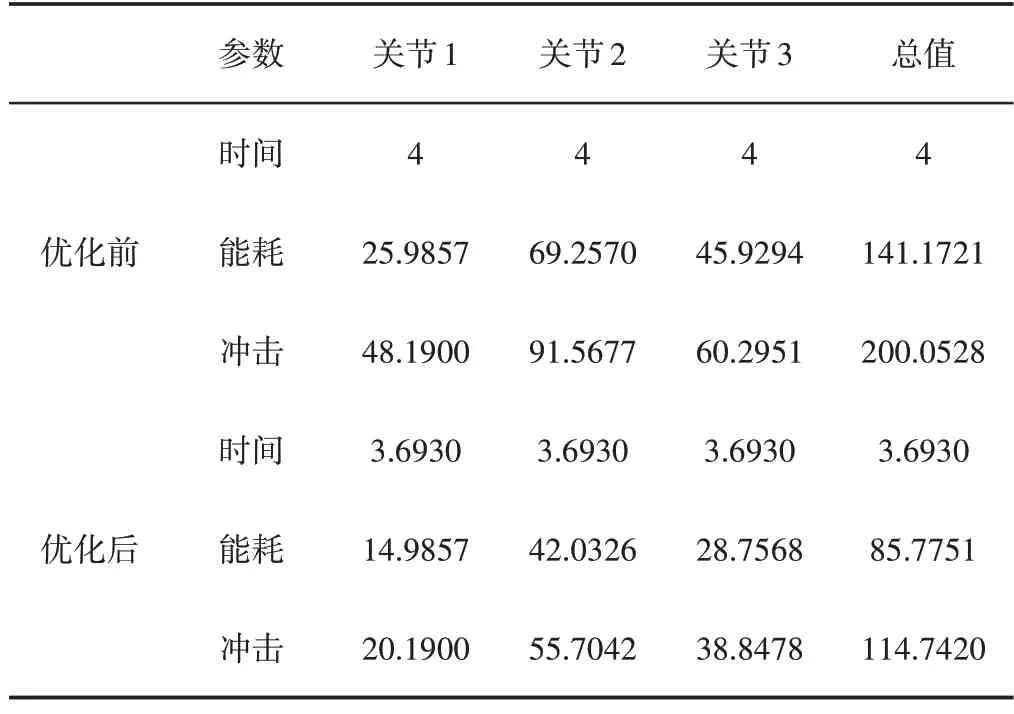
表3 优化前后对比Tab.3 Comparison Before and After Optimization

由表3中数据可知，经过优化，机械臂轨迹的运行时间、能耗及脉动冲击均有所下降，其中运行时间由4s减为3.6930s，减少了7.68%。总能耗由141.1721 减少为85.7751，减少了39.24%。脉动冲击由200.0528 减少为114.7420，减少了42.64%。由以上数据可以看出，经过优化，机械臂轨迹的运行时间、能耗和冲击均有较大的减少，说明了这里优化方法的有效性。

5 结论

这里针对机械臂轨迹的多目标优化问题，提出了非支配排序高斯粒子群优化方法。以运行时间、能耗和冲击为目标建立了多目标优化模型，使用非支配排序高斯粒子群算法求解，得到了优化结果，实现了效率、能耗、冲击的减少和优化。