融合改进RRT和DWA算法的移动机器人路径规划

刘紫燕，张 杰，袁 浩，梁 静

（贵州大学大数据与信息工程学院，贵州 贵阳 550025）

1 引言

路径规划作为机器人领域的重要研究内容之一［1］，其目标是让机器人按照一定准则从出发点到目标点搜索一条最优的无碰撞路径［2］。根据对环境中有用信息的掌握程度不同，机器人路径规划可分为全局路径规划及局部路径规划［3］。全局路径规划是机器人了解其所处环境的所有信息并能求解出静态环境下的最短路径；而局部路径规划则是不完全掌握环境信息，需在移动的过程中根据传感器信息调整路径［4］，主要用于解决动态场景下的避障问题。由于实际环境复杂多变且可能存在未知障碍物，全局路径规划无法满足其性能要求。因而局部路径规划成为研究热点，如何提高实时性和避障能力适应环境是尚待解决的问题。

传统的局部路径规划算法有人工势场法［5］、神经网络算法等，这些算法的计算复杂度高，且在实际场景下存在缺陷［6］。文献［7］提出一种基于Frenet坐标系的局部路径规划方法，采用代价函数选取最优轨迹，从而保证汽车行驶的安全性和平顺性，但该方法在复杂环境下的性能有待提高。近年来，动态窗口法（Dynamic Window Approach，DWA）由于具有计算量小、反应迅速、可操作性强等优点被广泛应用于机器人局部路径规划中［8］。文献［9］提出参数自适应的DWA算法，通过自动调整速度权值以自适应环境的变化，在稠密障碍物环境下表现出优越的性能，但没有考虑动态障碍物情况下的避障问题。此外，DWA常与其它优化算法结合以获得更好的性能［10］。文献［11］将改进A*算法与动态窗口法结合，在A*算法中引入关键点选取策略，基于动态窗口法构造实现全局最优路径的评价函数，在避免动态窗口法陷入局部最优的同时保证路径规划最优，但是在高维场景下计算复杂度高。文献［12］将目标偏向RRT与动态窗口法结合，在提高路径平滑度的同时缩短了行进时间，但是规划路径距离过长。文献［13］将角度变化因素添加到DWA轨迹评估函数中，使其具有更平滑的轨迹和更好的避障性能，但并未考虑到全局路径最优。

针对以上问题，提出一种融合改进RRT与DWA的局部路径规划方法。首先在RRT算法基础上，改进采样策略和优化路径以提高路径规划质量；然后改进DWA轨迹评价函数，将当前轨迹与全局路径的距离作为评价指标，充分利用全局路径，使行走路径最优的同时提高局部避障能力。

2 相关知识及建模

2.1 RRT算法原理

RRT算法是由S.M.Lavalle提出的一种高效的多维空间规划方法［14］。其算法流程，如图1所示。

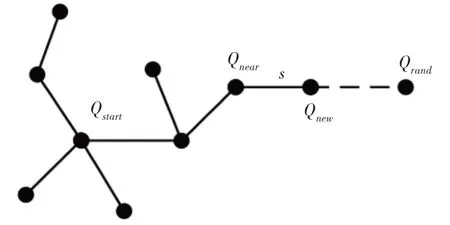
图1 RRT算法示意图Fig.1 RRT Algorithm Diagram

具体步骤如下：（1）初始化随机树T，设定起点Qstart，终点Qgoal，搜索步长s；（2）在地图中随机产生节点Qrand；（3）在随机树中找到离Qrand最近的节点Qnear；（4）从Qnear向Qrand方向扩展步长s得到新节点Qnew；（5）若Qnew在障碍物中或Qnew与Qnear连线与障碍物相交则舍弃Qnew；否则添加Qnew到随机树T中；（6）若‖Qnew-Qgoal‖＜s，则抵达终点，暂停搜索；否则返回步骤（2）。（7）从探索树的目标节点Qgoal回溯至Qstart，得到规划路径。

2.2 动态窗口法

动态窗口法是由文献［15］提出的一种局部避障算法，在速度空间内采样多组速度，在模拟周期内得到并评价所获得的轨迹从而选取最优轨迹［16］。最优轨迹对应的速度指令将驱动机器人移动，当机器人到达终点时，所有运动轨迹则构成了机器人实际行走的路径。

2.2.1 机器人运动模型

机器人运动模型，如图2所示。机器人在二维空间中移动，在机器人坐标系中，X轴方向速度为vx，Y轴方向速度为vy，角速度为ω。设t-1 时刻机器人的位姿为Xt-1=(xt-1，yt-1，θt-1)T，Δt时间内速度保持不变，将机器人坐标系下的位移量投影到全局坐标系，t时刻机器人位姿Xt［17］为式（1）所示：

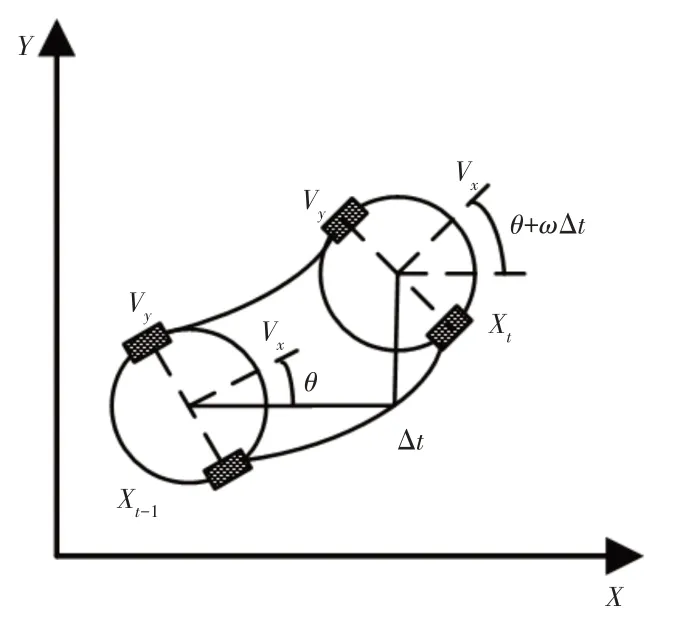
图2 机器人运动模型Fig.2 Robot Motion Model

2.2.2 速度采样

在速度(v，ω)的二维空间内存在无穷多组速度，可以通过机器人自身性能和环境条件将速度限制在一定范围内。通常由下述三个条件约束机器人的速度范围［18］：

（1）速度范围

机器人最大速度为vmax，最小速度vmin，最大角加速度为ωmax，最小角速度为ωmin，则机器人的速度(v，ω)如式（2）：

（2）电机性能

（3）制动距离

为了保证机器人在移动过程中的安全，防止机器人与障碍物的相撞，机器人的速度需保持在一定范围内，速度(v，ω)约束条件如式（4）所示：

式中：dist(v，ω)—速度(v，ω)对应轨迹上与障碍物的最近距离，此条件的目的是使机器人在遇到碰撞障碍物时停止运动。

2.2.3 评价函数

如前文所述，DWA算法在速度空间内采样得到多组运动轨迹，然后通过轨迹评分从多组轨迹选取最优轨迹，机器人运行最优轨迹对应的控制参数即可沿最优轨迹运动直至到达目标点。在速度(v，ω)下的轨迹总体评价函数，如式（5）所示：

式中：heading(v，ω)—方位角评估函数［11］，表示当前速度产生的模拟轨迹末端方向与目标点之间的角度［18］；dist(v，ω)—距离评价函数，表示当前速度对应轨迹上与障碍物的最近距离，采用曼哈顿（Manhattan）距离；velocity(v，ω)—速度评价函数，表示当前速度大小；σ、α、β、γ—各评价子函数的系数。设置该评价函数的目的是使机器人在避开障碍物的同时朝着目标点以较快速度行驶，从而保证局部规划效率。

3 改进路径规划算法

3.1 改进RRT算法

3.1.1 改进采样策略

传统RRT算法在机器人状态空间中随机产生新节点，采样效率低且路径质量较差［19］。这里提出改进采样策略，其核心思想是目标点Qgoal和随机产生的节点Qrand对随机树产生引力，两个节点一同引导随机树生长［20］。新节点Qnew不再只由随机节点Qrand决定，而且还受Qgoal的影响，如图3所示。通过此方式以改善原算法的随机特性从而提高搜索效率。新节点Qnew的产生，如式（6）所示。

图3 采样策略示意图Fig.3 Sampling Strategy Diagram

式中：new.X—在二维地图中新节点的横坐标；new.Y—新节点的纵坐标；near.X—最近节点的横坐标；near.Y—最近节点的纵坐标；s—扩展步长；θ1—Qnear与Qrand连线与X轴的夹角；θ2—Qnear与Qgoal连线与X轴的夹角；α、β—比例系数。

3.1.2 路径优化

改进RRT算法生成的路径包含多个转折点，并非最优。为提高路径质量，可优化处理路径。假设算法输出的路径由一系列路径点P={si}(1 ≤i≤N)组成，其中，si表示第i个路径点坐标(xi，yi)，为了缩短路径，取si+2和si的中间点代替原来的路径点si+1，如式（7）所示：

其中，得到的路径仍不够平滑，为了提高路径平滑度以便机器人转弯和移动，采用三次贝塞尔曲线对路径进行平滑处理。从路径P中确定（n+1）个点的位置Fi=(i=0，1，…，n)，可构造（n+1）阶贝塞尔曲线，如式（8）所示：

式中：Fi—Bezier曲线的控制点；n—Bezier曲线的阶数；t—控制参数，其取值范围为［0，1］；基函数Bi，n定义如式（9）所示：

若式中n=3，则得到三次贝塞尔基函数，如式（10）所示：

所以，三次贝塞尔曲线可表示为式（11）：

3.2 融合改进RRT算法和动态窗口法

传统DWA算法只在当前环境下选择最优速度，得到的路径是局部最优并非全局最优，若遇到U形障碍物或角落，机器人有可能陷入困境［21］，从而降低导航效率甚至导航失败。

结合全局路径规划和局部路径规划的优点，这里提出改进RRT和DWA融合的局部路径规划算法［22］。改进DWA的轨迹评价函数，使机器人在避障的同时跟随全局路径，从而充分利用全局路径最短。

在（10×10）m的二维地图上测试DWA算法的避障性能，如图4所示。设定起点为（0m，0m），一种色标记点为终点位置（10m，10m），黑色区域代表障碍物，在起点到终点的必经路径中存在U形障碍物。机器人从起点向终点运动，到达U形障碍物区域内时速度逐渐变慢直至止步于此，究其原因是当机器人靠近U形障碍物时无法再搜索到有效路径而无法离开U形障碍物，则路径规划失败。上述实验表明DWA算法易陷入U形障碍物困境，不适用于室内复杂环境下的路径规划。

图4 DWA陷入U形障碍物Fig.4 DWA Trapped in U-Shaped Obstacle

为了解决上述问题，使用DWA算法在驱动机器人运动时充分利用全局路径信息，即在全局路径的指导下生成局部路径。在图4所示的地图进行实验，机器人在运动过程中跟随全局路径成功到达终点，其路径，如图5所示。图中一种色曲线为改进RRT的算法生成的全局路径，另一种色曲线为DWA算法在全局路径引导下生成的运动轨迹。对比图4、图5 可知，在复杂场景下，DWA算法与全局路径规划算法结合能根据全局路径信息可有效避开U形障碍物到达目标点，并且规划的路径为最优［23］。

图5 全局路径下DWA逃离U形障碍物Fig.5 DWA Escaping from U-Shaped Obstacles Under Global Path Planning

机器人在运动过程中朝向目标点运动，但是由于环境中存在障碍物，使得机器人易陷入障碍物区域中，式（5）中的方位角函数heading的作用是避免DWA算法陷入局部最优，用路径跟随评价函数Pdist代替方位角函数heading，提出改进的目标函数如式（12）所示：

式中：Obs—生成轨迹末端与障碍物的距离；

Gdist—生成轨迹末端与目标点的距离；

Pdist—生成轨迹末端与全局路径点的最短距离；

μ、ξ、ζ—系数。

所选择的轨迹使式（12）取得最小值，机器人选择一条与最佳路径保持接近的安全路线，并朝目标点以较快速度行进。

这里提出的改进融合算法流程图，如图6所示。包括全局路径规划和局部路径规划。使用改进RRT算法规划出从起点到终点的全局最优路径，DWA算法依此路径和环境状况输出机器人的最佳速度和运动方向，生成机器人运动的真实轨迹。

图6 融合算法流程图Fig.6 Flow Chart of Fusion Algorithm

4 实验结果与分析

4.1 仿真实验

仿真实验的硬件配置：笔记本电脑安装Ubuntu 14.04操作系统，CPU为i3-3110M，主频2.4GHz，运行内存为4GB。

本实验在ROS平台的Stage仿真平台，选取Maze迷宫地图。机器人工作环境为（10×10）m 的迷宫，如图7所示。三种算法的起始点坐标统一设置为（2m，2m），终点坐标为（9m，3m）。A*-DWA、Dijkstra-DWA 和改进RRT-DWA 算法的规划结果，如图7～图9所示。其中，一条路径代表全局规划路径，另一条路径为机器人的实际运动轨迹［24］。

图8 Dijkstra-DWA规划结果Fig.8 Path Planning Results with Dijkstra DWA

图9 改进RRT-DWA规划结果Fig.9 Path Planning Results with Improved RRT-DWA

对比图7～图9可知，A*算法与Dijkstra算法生成的路径不够平滑，部分路径呈锯齿状；而改进RRT 算法生成路径平滑度提高，证明了改进算法的有效性。这里算法与Dijkstra-DWA 和A*-DWA 算法相比的结果，如表1所示。由表1数据可知，这里提出的改进RRT-DWA 算法生成的实际运动轨迹长度更短，较A*-DWA算法缩短了约10.14%；同时，这里提出方法的行进时间更短，提高了规划效率。

表1 Maze地图仿真实验数据对比Tab.1 Numerical Results on Maze Map

4.2 实际环境实验

在完成仿真实验后，在实际场景下验证了改进算法的性能。以笔记本电脑作为上位机，将融合算法应用到基于ROS平台的移动机器人Turtlebot2上，使用深度相机Kinect获取外界环境信息，amcl 和gmapping 模块实现定位和构建二维地图，如图10 所示。这里的实验场景为实验室，首先用无线控制器控制Turtlebot2扫描室内环境，利用gmapping算法构建二维地图，地图尺寸为576*512像素；然后在建好的地图上实现路径规划，并将实验结果与A*-DWA和Dijkstra-DWA算法进行对比。

图10 Turtlebot2机器人平台Fig.10 Turnlebot2 Robot Platform

在ROS的Rviz可视化工具中显示二维地图和三种算法的规划路径［21］，A*-DWA算法、Dijkstra-DWA和改进RRT-DWA算法的仿真结果，如图11～图13所示。可以看出这里所提算法所规划的路径更短。三种算法在相同起始点下生成轨迹的路径长度、行进时间和平均速度，如表2所示。由表2的实验数据可知，与A*-DWA 和Dijkstra-DWA 相比，改进RRT-DWA 的路径长度缩短，行进时间明显减少，平均行驶速度较高，体现了提出算法在真实环境下的优良性能。因此改进RRT-DWA算法优于A*-DWA和Dijkstra-DWA。

表2 实验室环境下三种算法实验数据对比Tab.2 Numerical Results in Laboratory Environment

图11 A*-DWA规划结果Fig.11 Path Planning Results with A*-DWA

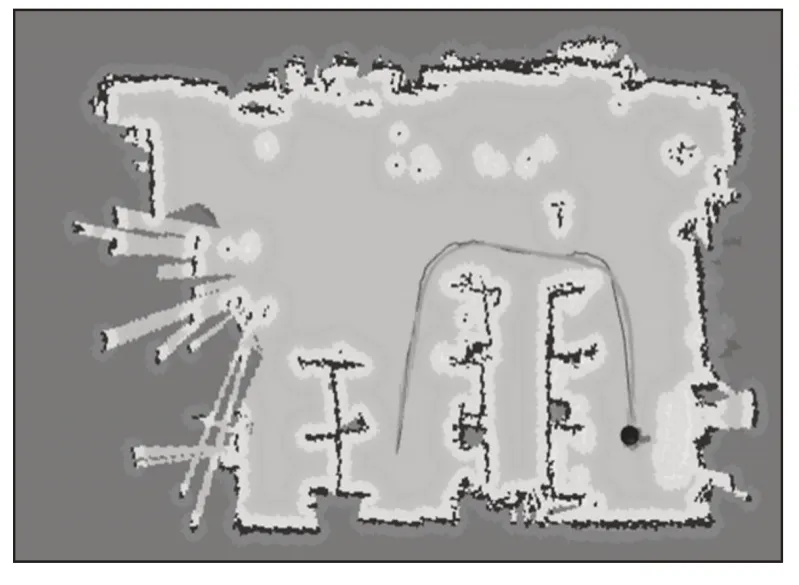
图12 Dijkstra-DWA规划结果Fig.12 Path Planning Results with Dijkstra DWA

图13 改进RRT-DWA规划结果Fig.13 Path Planning Results with Improved RRT-DWA

5 结论

这里将改进RRT算法与DWA算法融合，在兼顾全局路径最优的同时选择最优速度驱动机器人运动，不仅改善了路径质量，而且显著提升规划效率。与传统全局路径规划算法相比，这里算法由于能输出控制参数直接驱动机器人运动而具有较好的实时性，且规划的路径更优；与局部路径规划算法相比，这里算法不易陷入U形障碍物等困境，在复杂环境下适应性较高，且能保证规划路径的全局最优。这里算法充分利用全局和局部规划方法的优点，有效地解决了传统导航算法在已经规划好全局路线的情况下无法局部避障的问题，提高了机器人避障性能。