基于柔性射流动力的四通道飞行平台设计

胡建祥，王 瀚，蔡启才，薛 涛

（1.中国人民解放军第32381部队；2.武汉第二船舶设计研究所，湖北 武汉 430205；3.华中科技大学航空航天学院，湖北 武汉 430074）

1 引言

我国正处于迅猛发展的快速通道上，随着海上丝绸之路战略构想的提出和推进，我国在对外贸易中对海洋运输航线的依赖进一步增强，海基设备的应用将得到蓬勃发展，因此承载海上设备的稳定平台装置的重要性不断增强。在民用领域，舰载雷达设备或通讯设备往往需要相对于惯性坐标系保持某一角度的静止，须使用稳定承载平台设备隔离扰动。海上勘探设备或其他需要较高精度要求的设备使用时往往也需克服海面风浪等外在环境的干扰［1］。在军事领域上，稳定平台的研究同样具有十分重要的意义，安装在舰船上的武器设备往往会随着船体来回摆动，无法实现侦察和精准瞄准的目的，因此，必须使用海上稳定承载平台设备将设备和舰船产生的扰动相隔离，保证设备能够高精度地完成军事目的［1］。相对于车载［2］或机载平台［3］而言，海上或水面稳定平台摇摆幅度较大、运动频率低，舰船、潜艇等设备在水中的摇荡参数与船型、海况、风速、航速、遭遇角等因素有关。目前国内外研制的舰载稳定平台产品用于姿态稳定和目标追踪的二、三轴串联转动平台较多，技术相对成熟，主要用于舰船雷达天线、卫星通讯设备和舰载武器的姿态稳定，只能隔离舰船的左右摇摆和俯仰等摇动，平台承载能力较低。同时，舰载设备结构尺寸和重量较大，在一定程度限制了平台的实际应用。

针对海上或水面工况需求，提出了设计一种以射流为动力的稳定平台装置，用于隔离环境因素干扰，保证设备工作性能。该平台用于承载潜艇侦测观瞄设备或其他需水上水下功能联动的设备。设计方案参考四旋翼飞行器的结构采用轴对称布置，以中心为射流进水口，四周对称布置射流出水口，通过调节各出水口的水流量大小使得平台实现自稳功能，再以此作为主体的结构，在该结构上匹配设计出动力系统、液压制动系统、控制系统等。

2 射流飞行平台设计及建模分析

2.1 飞行平台的设计机理分析

所设计平台的框架结构和四旋翼构型具有一定相似性。四旋翼飞行器的构型通常呈轴对称布置，主要通过控制四轴电动机的转速来调整飞行器的姿势和速度，其四轴旋翼转动时产生的反扭矩则相互抵消［5］。旋翼无人机根据对称轴的不同，通常可分为呈十字交叉布置以及X型布置结构，如图1（a）所示。在旋翼无人机中，十字形布置往往机动性更强，X型布置可以更有效的抵消旋转扭矩，其稳定性更强［6］。而对于以水射流为动力的飞行装置而言，不会产生旋转力矩，往往需要有较快的响应速度，便于控制达到稳定状态，因此设计中采用十字型结构布局方案，此时控制飞行姿态仅需改变单一轴的动力大小即可。

图1 平台设计布局图Fig.1 Model Design of the Platform

平台如图1（b）所示，以中间端管道为射流进水口，此处水射流冲击力提供部分升力，而四周管道出水口的射流反作用力为升力，通过调节四周出水口的流量大小来使得平台在空中能够保持稳定，当1、3射流口流量发生变化时，其射流的反作用力发生变化，平台将进行俯仰运动，当2、4流量变化则进行滚转运动。将其与以空气动力的旋翼无人机相比，在该结构设计中，以射流为动力的平台装置没有横向力矩产生，因此无法实现偏航运动，但作为主要用于水面或海面上进行观瞄的平台而言，其目的是实现在复杂环境下能持续保持自身稳定，对平台的偏航运动以及前后左右移动幅度的功能要求较低，设计方案可满足基本需求。

2.2 平台的模型设计及分析

欧拉角度可以表示为一个坐标系到另一个坐标系之间的坐标位置变换，因此，也可以看作是一个坐标系分别绕另一个坐标系的X轴、Y轴、Z轴的转动，其转动的顺序不一样可得到不同的转化方程组。当动力系统工作时，射流进水口O的作用力主要作为推动平台的动力，当1、3处射流出口流量大小不一样时，其反作用力不相等，则平台将产生一个沿着Y方向转动的角度。同理，当2、4出水口水流量大小不一致时，将会产生一个以X轴为旋转轴的转动。由于以水射流为动力的平台中没有提供横向力或力矩，因此对于该平台的设计和研究过程中暂时不考虑偏航角度。

3 动力学计算分析及仿真

3.1 动力学分析

假定以地面坐标为参考坐标系，可分别建立在合外力F和合外力矩M作用下的线运动及角运动方程组：

式中：Ix，Iy，Iz—平台转置绕X、Y、Z轴的转动惯量；

Ixy，Iyx，Iyz，Izy，Izx，Ixz—其惯性积。

转动惯量I=mr2，其中，m为该承载平台的总体质量，r为平台的质点到转轴的垂直距离。由于可看作是高度对称平台，OXZ和OYZ平面均可以看作是轴对称平面，所以Ixy=Iyx=Iyz=Izy=Izx=Ixz=0。在力矩的作用下，平台将绕其质心做旋转运动，由平台动坐标系到地面参考坐标系之间的转化可以推算出，姿态角速率的变化量与在平台坐标系下的角速度投影到坐标轴上的三个分量（p，q，r）这两者之间的关系式：

在合外力的作用下，平台将发生位移运动，同样根据平台动坐标系到地面参考坐标系之间的转换矩阵可求得其运动方程组如下：

假设该平台为质量均匀的轴对称刚体，在机体坐标系下，对该飞行平台进行力和力矩分析，此时有：

平台动坐标下力矩M如下，式中：r—平台半径：

3.2 水动力模型的建立

由于射流出水口的水流表面是大气压，该处的作用力仅为水流的动力，出水口所受到的推力F可由下式计算，利用水动力机理，基于流体力学原理可以得到喷口作用力F(Qi)F与流量Qi的定量表达式关系：

根据连续性方程得：

式中：ρ—水的密度；Q—柔性射流平台稳定工作时的体积流量；u0—平台入口射流速度；u1，u2，u3，u4分别为柔性射流平台出口射流速度；A0、Ai—平台进出射流口处截面面积大小。

在设计中，通过液压系统装置调节各流量口半径r大小，来改变在各射流喷口面积A的大小。r为初始时各出水口的半径，li为液压杆伸入的长度，此时各四周出水口的横截面积为：

同时在各喷口处安装流量计可测得各喷口的流量数据Q，根据Qi=Aui，此时各进出喷口流量的速度u可知。得：

根据稳定平台姿态及作用力数据，控制系统将输出相应控制信号，信号经过液压制动系统控制液压杆li进行伸缩运动，以此达到调节射流力大小的目的，其力学关系式，如式（8）～式（11）所示。单个射流口作用力Fi与液压杆伸缩长度li、喷射流量Qi之间作用关系，如图2（a）实验台架模型所示。稳定平台的水泵供水原理示意图，如图2（b）所示。取自由水面与柔性射流平台进入出截面之间的水流为研究对象。根据伯努利方程，有如式（12）成立，式中H为水泵的扬程。

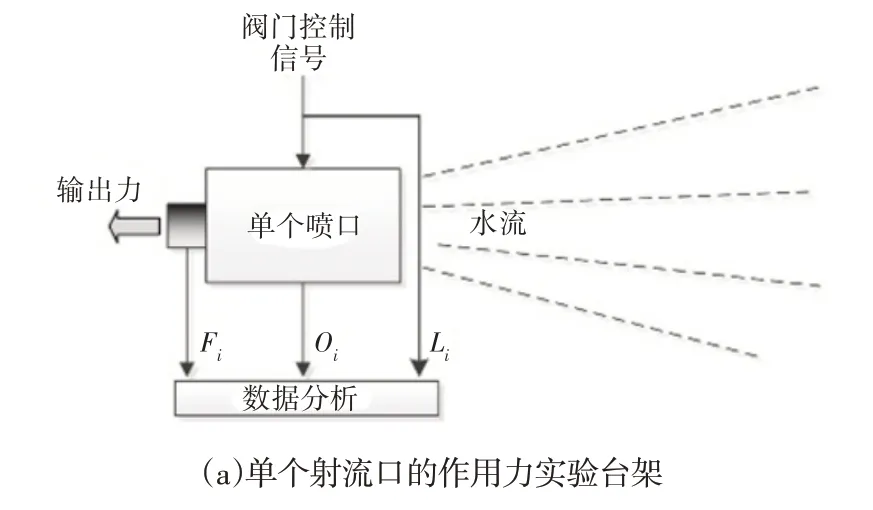
图2 柔性射流平台水泵工作原理图Fig.2 Schematic of the Flexible Jet Platform Pump

式中：ρghfi—平台输水管内的扬程压力损失；ρghfe式射流平台内部流动压力损失。水泵扬程与水泵功率有如下关系，其中，η—水泵工作效率。

由于平台尾喷管出口高度ze与平台引水进口端高度z1之间的高差相比射流平台飞行高度h很小，因此可以认为ze=zi=h，另外水泵进口端的自由液面可看成无限大，液面下降速度u1=0，p1为大气压，z1=0，可得：

此时对于射流进水口速度的大小为：

所以得进水口射流作用力为：

3.3 求解稳定状态关系

对该平台的动力学分析可实现其在稳定状态下的相关参数推导，可求解出稳定状态下具体参数的数学关系式。

当该平台飞行器处于稳定悬停状态时，根据式（6）、式（7）：

假设此时处于理想状态下各力保持相等状态即液压杆的推入长度li为一相同值，联立稳定状态下的数学表达式及水动力学的推导式，此时可求出在稳定状态下，水泵功率P、飞行高度h、以及液压杆推入长度li之间的关系式为：

根据设计需求，射流进水口的半径R为8cm；射流出水口半径r为6cm；水泵工作效率η取值为0.65；在动力学计算过程中，平台装置可看作是一个理想的圆柱形状，且其重力分布均匀，沿OXZ平面和OYZ平面均为结构对称，因此可知惯性积Ixz为0，同时根据转轴沿圆柱体转动惯量计算公式：

可求得Iz为6.25，与圆柱体中心垂直方向的转动惯量为：

求得Iz为3.3，联立式（3）得：c3=c7=0.3，c9=0.16。

设计中采用消防常用的聚氨酯水带作为平台的输水管路，水管的沿程水头损失与水力条件、管路材料等要素有关［7］。该材质的水带常被用于消防、船舶、水利、石化等众多领域中，聚氨酯材料水带主要采用高强度合成的化学纤维织成，并以橡胶作为水管衬里。在高压作用下，纤维和橡胶两种材质将紧密的结合，使其内部水流阻力较小，同时具有耐高温腐蚀，耐老化等特点。

由单位长度的管道沿程水头损失计算公式以及管道局部水头损失计算的相关参数［8］，可求得此时平台输水管内的沿程损失hfi大小为10.1m，射流平台内部流动损失hfe大小为2.7m；重力系数g取值9.8N/kg；代入后能得出水泵功率P、飞行高度h以及液压杆推入长度li的数学关系式：

当平台重量和负载重量之和为100kg 时，且使得平台飞行器平稳飞行高度为3m，理论上液压杆的行程范围应在0cm＜li＜6cm之间，不能使射流出水口完全关闭，为保证液压杆的使用寿命以及射流口调节部件的正常使用，可将行程范围设置为0cm ＜li＜5cm。

当该平台处于理想状态下，各力Fi保持相等状态，即液压杆的推入长度li为一相同值，此时存在三个未知变量：水泵功率P、飞行高度h、以及液压杆推入长度li，其数学关系式，如式（21）所示。在实际运行过程中，水泵功率P、飞行高度h其中之一往往被设定为固定常量，因此可对关系式进行控制变量分析。当我们将飞行高度设定为所需固定量，为便于观察理解，可将式（21）以数学曲线形式表达，假定保持飞行高度为3m时，此时可得稳定状态下关于水泵功率P和控制液压杆运动进程li之间的曲线图，如图3（a）所示，随着液压杆li的长度推入，射流口面积减小，维持飞行高度为3m 时，平台所需功率在不断减小。

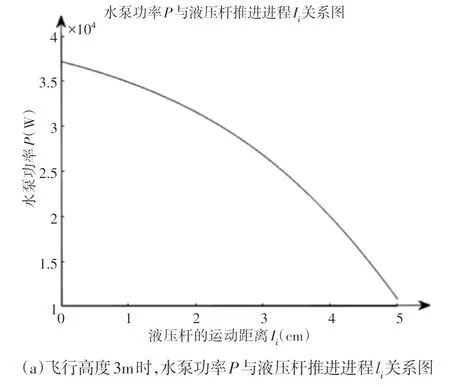
图3 液压杆进程与水泵功率/飞行高度关系图Fig.3 Relation Between Hydraulic Rod Advancement（li） and Power/Altitude

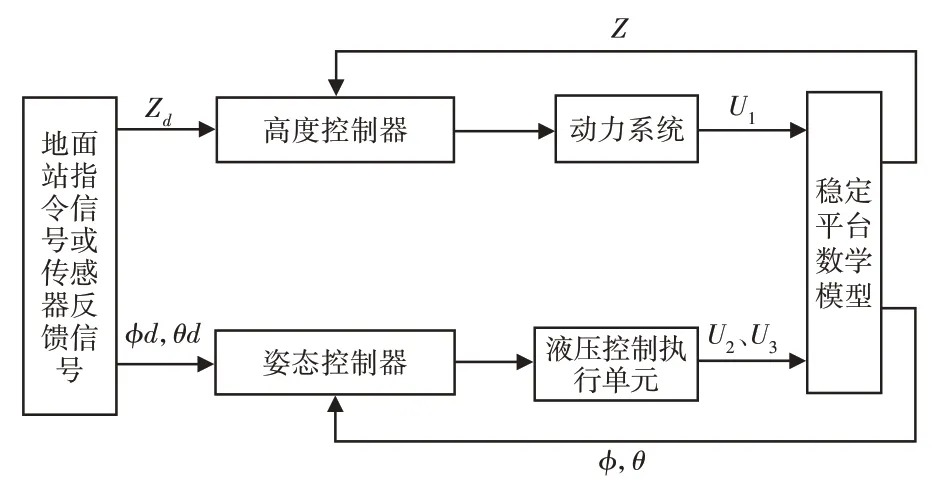
图4 平台飞行控制示意图Fig.4 Schematic of Platform Flight Control

同理，当设置在一定功率下运行，平台自重和载重量为100kg时，可以得到飞行高度h（h＞0）和液压杆推进的进程li之间的关系，由于在考虑水管路能承受的最大压力限制以及平台自身的耐用性等实际情况，需要将平台的飞行高度限制为在一定范围内。可设定实际飞行高度h的范围0＜h＜10m，当飞行高度达到10m此时再继续推进液压杆行程则可能造成输水管路压力过大、射流口流量调节装置严重形变等问题。稳定状态下，将水泵功率设置为30kW时，式（21）可用如图3（b）所示的飞行高度与液压杆进程曲线关系表示。图中显示，飞行高度随着控制液压杆行程的推进而不断升高，且其升高的变化率随液压杆的推进呈现增大的趋势。

4 控制系统仿真设计

一般飞行器在空间坐标系下的基本动作包括悬停、滚转、俯仰、偏航及竖直和水平方向位移［10］，平台基于用途和动力特性，基本动作包括悬停、上升、降落、滚转以及俯仰。设计中平台主要通过调整射流口力的大小，使得平台能稳定悬停在某一高度，同时具有较强的自稳定性。从其动力学特性以及平台的结构特征来看，飞行姿态的控制主要依赖于四路出水口射流反作用力的大小变化，飞行高度的变化同时依赖于中间射流进水口的推力的变化，即和水泵的功率大小有关。基于以上动作状态的分析，可设计如下控制结构。

针对设计平台的模型结构以及控制目标需求，在进行飞行平台设计时，需要注意以下问题：

（1）模型建立问题

在平台飞行过程中，由于平台内部射流水柱流动的不均匀性可能导致控制系统无法实现目标效果，给控制系统设计增加了难度。

（2）连接水管干扰问题

与平台相连接的输水软管摆动可能给平台的稳定飞行带来干扰，尤其在初始供水阶段，管路内水柱的冲击方向和变化难以直接预测，具有不确定性。根据设计的平台模型，针对以上存在的问题，对比以上常用控制算法的特点，依据动力学分析及控制结构设计图考虑控制算法。PID控制程序简单，稳定可靠，同时能用于系统控制模型具有不确定性特点的对象。因此，设计的控制系统主要使用了PID控制算法。

4.1 PID控制器设计

设计的控制系统主要使用了PID控制算法，对该平台的控制方案可将高度控制器、姿态控制器分离设计［10］。若定义三个独立的输入控制量分别为U1，U2，U3，状态空间方程为：

当平台处于悬停状态时，其高度控制系统的状态方程为：

假设zg为期望高度，建立高度控制器，如图5（a）所示。

图5 高度、俯仰角度和滚转角度控制器Fig.5 PID Control of Altitude，Pitch and Roll

对于该平台来说，设计姿态控制的目标是使得平台在一定的干扰环境下仍能保持平稳的悬停状态，因此当平台处于小扰动下的稳定状态时，其滚转和俯仰角度的状态方程简化后可表示为：

与高度控制子系统相似，假设θg，ϕg为期望俯仰角度和滚转角度，同样使用PID 控制方法设计，可得姿态控制器，如图5（b）、图5（c）所示。因此可以得到{z，θ，ϕ} 三个状态向量的PID控制器：

4.2 控制器仿真及分析

设计通过运用MATLAB仿真软件对该平台进行数学模型的建立以及控制系统的仿真分析，使用PID控制算法搭建整体控制逻辑的框架图，然后对框架内各个子系统进行建模设计，通过完整的控制仿真，观察平台在悬停状态下的姿态数据响应效果。

为了使整体逻辑更加清晰，便于查看和修改，部分功能封装为子系统。在参数设置时，平台重量已知，同时水泵以固定功率工作时，射流入水流量及射流入水口作用力F0为已知量。平台的悬停状态为其他动作基础，因此可建立当平台处于小扰动状态时，其控制系统仿真结果，如图6所示。

图6 平台控制系统仿真结果Fig.6 Simulation Results of the Platform Controlling

在进行悬停状态控制系统仿真时，平台飞行高度设为3m，根据控制系统的仿真结果可以看到在3s 左右高度通道值Z达到稳定，其滚转角度和俯仰角度也在此时趋于平稳状态，因此从仿真结果看，系统最终能够达到自身稳定的悬停状态，该系统具有可控性。

5 结论

首先提出了基于水射流为动力的平台设计思路，并进行了结构及关键尺寸设计，然后对该平台进行动力学的分析，可知当平台处于稳定状态下，水泵功率P一定时，飞行高度h随着液压杆推进距离的增大将会逐渐增大，理论上能够实现通过控制液压杆的推进距离对平台的位置及姿态进行控制。随后建立了系统控制模型，经过控制算法对比分析后，搭建Simulink控制仿真程序，得到了稳定状态下的姿态数据和稳定曲线均趋向平稳状态，验证了该方案理论上的可行性，为该平台的后续链路设计和实物搭建提供了理论基础。