高次有限元格式数值求解Stokes 方程

丁 晓，陈 璐，江 山

（南通大学 理学院，江苏 南通 226019）

20 世纪50 年代末，受大型水坝计算问题的启发，冯康院士创建了系统化、理论化的有限元法。随着计算机技术的飞速发展，有限元法已广泛应用于求解热传导、电磁场、流体力学等连续介质问题。Stokes 方程可以描述雷诺数很小时液滴在黏性流体中的运动问题，近年来被广泛关注。利用有限元法求解Stokes 方程一直是计算数学和流体力学领域的热点，其研究取得了诸多成果[1-7]。比如：文献[1]考虑非定常Stokes 方程，将流函数方程和涡度方程分开讨论，再用混合有限元法进行误差估计；王小军和祝家麟[2]针对含开边界的二维Stokes 问题研究Galerkin 边界元解法，数值模拟了不可压黏性流体的绕流；吴妍等[3]使用自适应变分多尺度方法对Stokes 方程进行优化，将细尺度问题分解为若干互不影响的子问题再进行求解；段献葆等[4]基于Stokes 问题，提出了一种与优化方法相耦合的自适应网格方法；文献[7]借助差商法研究了非线性稳态Stokes 系统的弱解对高阶分数的可微性；等等。此外，作者课题组应用有限元法与多尺度计算，针对二维奇异摄动边界层问题[8]、非稳态扩散方程[9]、弹性力学方程[10]等进行了一系列富有成效的理论分析和数值验证。但上述成果均未涉及Stokes 方程求解，且所得精度或效率仍有提升空间。本文主要针对Dirichlet 边界下的二维矢量型Stokes 方程，基于有限维逼近无限维的数值计算思想和变分虚功原理，将原方程区域离散化分割成有限个单元，再对每个局部单元选定二次基函数，形成并组装信息矩阵和载荷向量，进而针对矢量型方程求解代数方程组，并进行图像绘制和误差分析，即采用高次有限元格式处理Stokes 方程，以期得到更好的数值精度、更高的稳定收敛阶数。

1 Stokes 方程与泛函空间

考虑二维矢量型Stokes 方程

类似地，应力张量也可写为

二维区域Ω=[0，1] × [-0.25，0]，∂Ω 是其边界。

再进行分部积分，有

2 有限元格式与二次基函数构造

有限元法的基本思想是用有限维空间去逼近无限维空间，在保证数值解正确性的前提下，进一步考虑数值解的稳定性与收敛性。

下面构造所需的有限元空间。针对流速与压力，分别考虑有限元空间Uh⊂H1（Ω）和Wh⊂L2（Ω），记Uh0是由Uh在边界上值为零的所有函数张成的空间。有限元法的变分形式为：

接着，对区域Ω 进行网格剖分，用三角形单元将其离散化。对每个局部单元选取二次基函数，形成并组装信息矩阵A 和载荷向量，求解代数方程组，得到流速的有限元解。

为了取得更优越的模拟效果，在局部单元上采用二次元基函数。设初始的三角形单元E=ΔA1A2A3，再取三条边的中点A4、A5、A6，见图1。

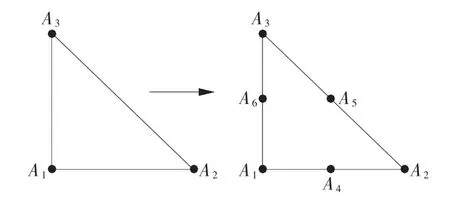
图1 线性单元3 节点与二次单元6 节点的对应关系

定义参考单元上的6 个二次元基函数

使得对任意i，j=1，…，6 都有

比如，对于ϕ1，将三角形单元的六个点代入，有

解六元一次方程组，可得

所以，ϕ1=2x2+2y2+4xy-3x-3y+1。类似地，经上述步骤可以求得全部6 个基函数，即

由此可使总刚度矩阵的稠密程度更高，每个单元与节点间的联系相对线性基函数而言也更紧密，二次基函数的有限元解能更好地反映Stokes方程的精确解分量。

3 数值算例

为验证有限元法求解二维Stokes 方程的可行性与有效性，通过实际算例和MATLAB 编程计算相应的数值精度和收敛阶数。

令黏度系数v=1，在区域Ω=[0，1]×[-0.25，0]，边界∂Ω 上有则右端为

为了直观展现有限元解与精确解之间的近似程度，用MATLAB 画出单方向剖分数N=32 时的精确解的两个分量u1，u2如图2，二次有限元解的两个近似分量u1h，u2h如图3，以及其绝对误差的三维图如图4。由图可见，有限元解与精确解非常接近，且u1的最大误差数量级为3×10-6，u2的最大误差数量级为6×10-7，验证了有限元解逼近精确解的可靠性。

图2 精确解的分量u1，u2 图像

图3 有限元解的分量u1h，u2h 图像

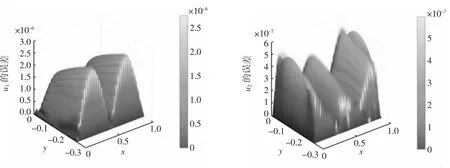
图4 精确解与有限元解之间的绝对误差三维图像

通过计算得到三种不同范数意义下有限元解与精确解之间的数值误差和收敛阶，见表1。由表1 可见：二次元基函数格式下该算例的L∞范数和L2范数都达到了三阶收敛；H1半范数达到了二阶收敛，并且最高精度可以实现10-8数量级。数值实践结果充分表明，高次有限元格式对于数值求解Stokes 方程十分有效，得到的结果也很理想。

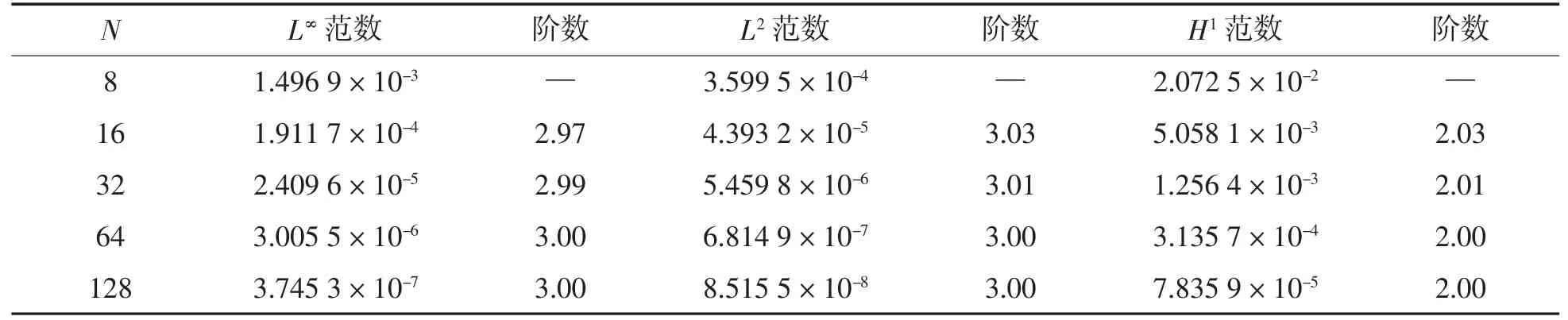
表1 二次有限元格式的误差范数及其收敛阶数

综上可知，通过高次有限元格式的理论构造和数值模拟，可直观系统地展示二次元基函数下有限元法求解二维矢量型Stokes 方程的有效性和精确性，得到了高精度、高收敛的一致稳定化数值模拟结果。