第一性原理研究Sr（Fe1- xPtx）2As2 中的反铁磁抑制与共存

李 力，王红丽，王伟芳，樊丽丽，王金环，陈立宇，郝璞玉，贾东芳

（唐山师范学院数学与计算科学学院，河北 唐山 063000）

1 引 言

继铜酸盐之后，铁基超导体的发现掀起了超导研究的新高潮.在F 掺杂LaOFeAs 中观察到超导现象[1]，超导体的转变温度（Tc）约为26 K.随后DOFeAs（D＝Ce，Sm，Nd，Gd等）的报告显示Tc超过45 K[2]，其中Sm[O1-xFx]FeAs 的Tc达到55 K[3].随后，122 家族[4-6]的EFe2As2（E＝Ba，Ca，Sr）迅速进入研究人员的视野，更容易制备出高质量的晶体样品[7]；其中，SrFe2-xMxAs2（M＝Ru，Co，Ni，Rh，Pt 等）的掺杂也先后得到了研究[8-9].在一些基本性质方面，实验报道单晶和多晶样本的研究得出了不同的结论[9-10]，因此借助理论计算得出的结论具有特殊的意义.

在铁基超导体的研究中，逐渐形成了相对统一的认识：反铁磁（AFM）序与超导态之间存在竞争关系[11].为了抑制AFM 诱导超导，通常采用碱金属或过渡金属掺杂[12]和施加外压[13].虽然超导态与AFM 之间的竞争已被广泛认识，但高温超导的机理仍在探索中.在对122 家族的研究中，有的掺杂实验发现了超导态和AFM 序在微观水平[14]的共存，也有发现了相分离的情形[15].从理论上讲，AFM 序在超导掺杂范围内是否仍然存在已成为我们感兴趣的问题之一.

在电子结构和磁机理的研究中，一种观点认为电子费米面（FS）和空穴费米面的嵌套决定了低温下反铁磁条纹的排列顺序[16-17]，另一种观点认为自旋构型的形成是由于原子[18]的超交换相互作用.对电子结构的分析同样应用于对铁基超导塌缩相和非塌缩相的研究中[19].本文主要研究了在0 K 下，Pt 掺杂SrFe2As2布里渊区中心Γ 和Z 点附近费米面嵌套的变化，这种变化反映了AFM 和超导竞争在铁基超导体中的作用.同时，为了说明Pt 掺杂对超交换的影响，利用了Heisenberg 模型计算交换耦合常数.

2 模型与计算方法

采用基于密度泛函理论的CASTEP 程序包进行计算.SrFe2As2的低温结构为Fmmm[20]，SrFe2As2的晶格常数（Å）为a＝5.578 3（0），b＝5.517 5（0）和c＝12.296（5）.这里使用含有20 个原子的1×1×1 超胞来进行计算.

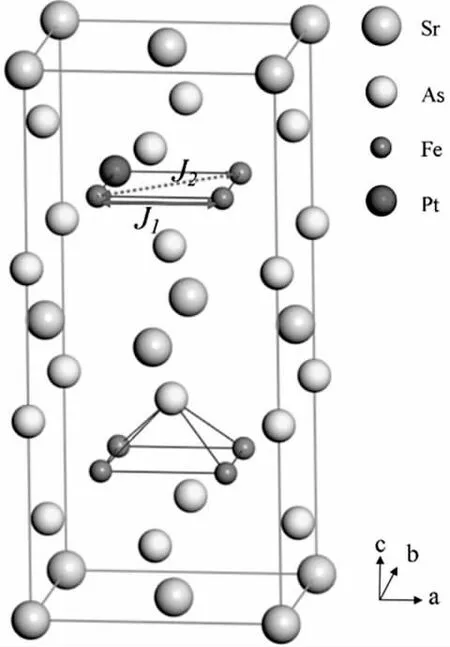
图1 Pt 掺杂SrFe2As2 时20 个原子超胞模型与Fe 平面上最近邻和次最近邻交换耦合常数J1，J2

基于密度泛函理论，采用平面波法进行计算.布里渊区采样由12 ×12 ×6 Monkhorst-Pack k 点网格给出.利用广义梯度近似（GGA-WC）中Wu 和Cohen 提出的交换相关函数[21]，计算出了不同磁序的体系能量.在计算中，截断能设置为450 eV，自洽收敛精度采用2×10-5eV/atom，对原子最大受力的收敛准则为0.05 eV/Å.最大位移和最大应力分别为2×10-4nm 和0.1 GPa.初步结果表明，在较高的收敛准则下，上述参数保持不变.

3 结果与讨论

我们对SrFe2As2和Sr（Fe1-xPtx）2As2的结构进行了优化，优化后的晶格参数和磁矩随共线AFM 的变化如表1 所示.结果表明，Pt 的掺杂使Fe 的磁矩由1.92 μB/Fe 降低到1.828 57（1）μB/Fe.在优化结构后，我们计算了四种不同磁序的体系能量：棋盘反铁磁序（AF1），共线反铁磁序（AF2），铁磁序（FM）和无磁态（NM）.我们发现共线AFM 序的体系能量最低（见表2）.这意味着共线反铁磁序在低温下为基态，这与文献[22]相同.

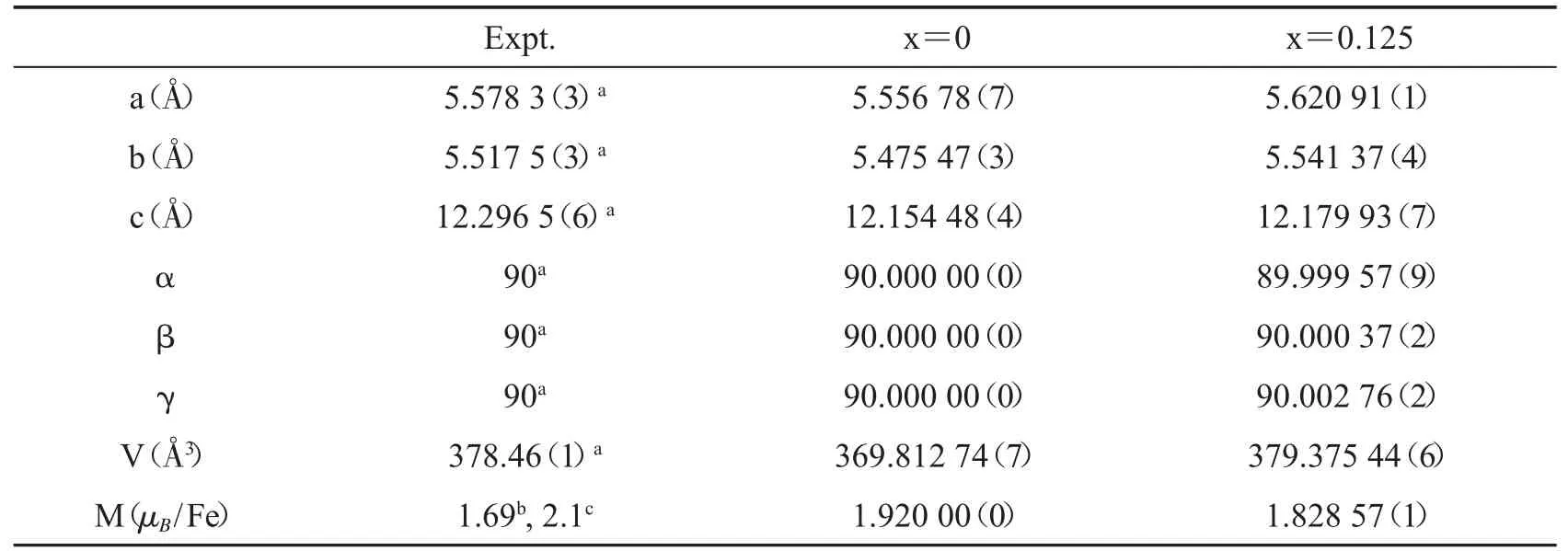
表1 共线反铁磁序下，优化了Sr（Fe1-xPtx）2As2 在x＝0 和x＝0.125 的晶格参数和Fe 磁矩M.

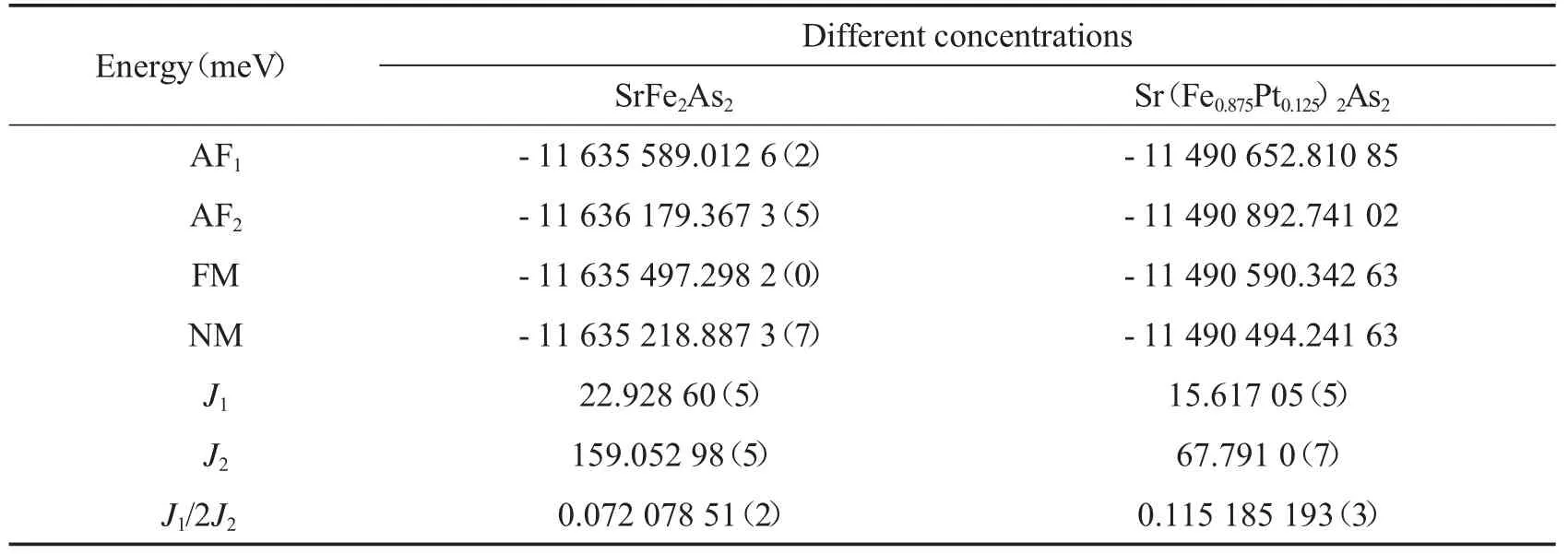
表2 Sr（Fe1-xPtx）2As2 在x＝0 和x＝0.125 时的J1、J2，以及Sr（Fe1-xPtx）2As2（x＝0 和x＝0.125）在四种不同磁序下的总能量：棋盘AFM 序（AF1）、共线反铁磁序（AF2）、铁磁序（FM）和非磁性态（NM）.

在基态下，计算了Sr（Fe1-xPtx）2As2（x＝0，0.125）的DOS 和PDOS，结果如图2 所示.从图中可以看出，DOS 主要来自于Fe 3d 和As 4p 轨道的贡献，而在费米能级（EF）附近，DOS 主要来自于Fe 3d 轨道的贡献.当掺杂Pt 达到x＝0.125 时，费米能级向导带方向移动，N（EF）由12.336 1（7）states/eV 增加到12.804 0（8）states/eV.计算表明，Fe 3d与As 4p杂化带宽度由9.318 0（8）eV（SrFe2As2）增加到10.312 0（4）eV（Sr（Fe0.875Pt0.125）2As2）.同时，掺杂后各Fe 的磁矩由1.92 μB/Fe 降低到1.828 57（1）μB/Fe，这意味着Fe 3d 的电子局域化特性变弱，而流动性增强.

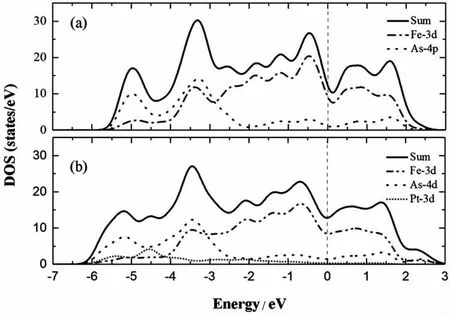
图2 共线反铁磁序下，Sr（Fe1-xPtx）2As2 在x＝0（a）和0.125（b）的DOS 和PDOS 图

能带图见图3.未掺杂时，SrFe2As2自旋向上和自旋向下的能带是重合的，在Γ 和Z点，分别有一条价带向上通过费米能级.随着Pt 的掺杂，费米能级向上移动，这与分析前面的DOS 图时得到的结论同样.费米能级的上移使得部分原本在Γ 和Z 点穿过费米能级的能带，此时完全位于费米能级之下，而部分导带向下弯曲并折叠通过费米能级.Pt 掺杂使价带在M 和A 点附近向上越过了费米能级.

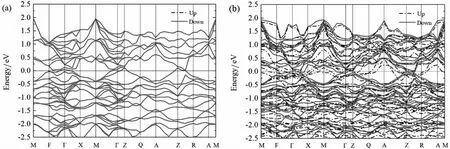
图3 共线反铁磁序下的能带图.（a）SrFe2As2 的能带结构.（b）Sr（Fe1-xPtx）2As2 在x＝0.125 时的能带结构

在图4 中绘制了SrFe2As2在0 K 时的费米面.SrFe2As2的费米面在Γ 与Z 点形成了嵌套关系.随着Pt 的掺杂，原来Γ 与Z 处的空穴型费米面消失了，并演化为电子型费米面.空穴型费米面的嵌套只形成于M 点和A 点附近.

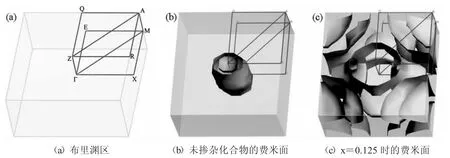
图4 Sr（Fe1-xPtx）2As2 的费米面图

为了反映掺杂对超交换的影响，本文利用Ma 等[26]提出的Heisenberg 模型计算了交换耦合常数，如表2 所示.结果表明，掺杂后J1和J2的交换耦合常数降低，磁矩和交换耦合常数的降低表明反铁磁序被抑制.计算表明，Sr（Fe1-xPtx）2As2（x＝0，0.125）的J1/2J2＜1，说明它们均为共线反铁磁序.同时，有研究工作[27]已经表明，当x＝0.125 时Sr（Fe1-xPtx）2As2处于超导状态，此时我们的计算结果可为超导态与共线反铁磁共存提供支持.

4 结论

借助CASTEP，我们研究了SrFe2As2在0 K 下的电子结构和磁学性质.DOS 分析表明，Pt 掺杂削弱了Fe 3d 轨道电子的局域性，增强了电子巡游性.随着Pt 的掺杂，布里渊区中心Γ 和Z 点附近的空穴费米面嵌套转变为电子费米面的拓扑结构.利用海森堡模型研究了Pt 掺杂对超交换的影响，超交换耦合常数J1和J2随Fe 磁矩的减小而减小.掺杂Pt 有助于抑制SrFe2As2中的AFM.对于SrFe2As2，计算表明J1/2J2＜1，这表明，无论从四种不同磁序下的体系能量比较，还是从Heisenberg 模型来看，共线反铁磁序均为基态.同时计算表明，在超导浓度（x＝0.125）时J1/2J2＜1，这意味着共线反铁磁序被抑制，但仍然存在.这些结果将有助于理解铁基超导体中AFM 与超导态之间的关系.