一种基于结构约束的点线特征融合SLAM 算法

马广飞,邵 巍,李晋屹,刘祥鹏

(青岛科技大学 自动化与电子工程学院,山东 青岛 266061)

SLAM 算法用于估计相机位姿,同时重建周围的未知环境。它们在自主机器人、自动驾驶汽车和增强、虚拟现实等方面具有广泛应用价值[1]。特征点SLAM 从图像中提取特征点,通过特征点匹配计算相机位姿,是视觉SLAM 的主流方法[2]。DAVISON 等[3]提出的MonoSLAM 通过提取每帧特征点估计相机位姿,但因逐帧对特征点进行提取,计算成本很高。ORB-SLAM2[4]是由Mur-Artal和Tardos提出的开源SLAM 算法,该算法以其速度快和精度高成为比较SLAM 算法性能时常用基准之一。特征点SLAM 算法涌现出许多优秀的算法,但这些算法在低纹理环境中依然面临严峻挑战[5]。线特征具有较好的光照不变性和旋转不变性,可以提供更多的几何结构信息[6]。NEIRA 等[7]首次将直线特征应用到单目SLAM 算法中,但该算法因线特征提取精度不高导致定位精度不理想。随着LSD[8]、EDLines[9]线段提取算法以及LBD[10]线特征描述符等算法的提出,基于线特征的SLAM 算法获得广泛研究。然而,这些基于线特征的SLAM 算法仍存在端点位置不准确、几何约束不明确等问题,过多的误匹配反而给系统带来更多的累积误差[11]。

研究人员为了得到性能更优的SLAM 算法,将点特征与线特征结合,提出了一些基于点线特征融合的视觉SLAM 算法。GOMEZ-OJEDA 等[12]提出了PL-SLAM 算法,该算法在点特征稀疏的场景性能较好,但其存在数据冗余和较大的误匹配问题。LI等[13]提出一种SLD 线段提取算法,将点线特征加入后端优化,有效解决了优化中的不稳定问题。现存点线特征SLAM 仅使用线特征的简单几何信息,没有利用线特征的结构性约束优化特征位置与相机位姿,造成了结构约束信息的浪费。针对上述问题,本研究提出了一种基于结构性约束的点线融合SLAM(point-line feature fusion based on structural constraints SLAM,PLSC-SLAM)算法。该算法充分利用点特征和线特征的结构性约束的优点,提高了SLAM 的精度和稳定性。具体开展的工作包括:1)利用RANSAC 方法鲁棒拟合空间直线,减小空间直线位置误差。2)将直线分为平行线与垂线,以此作为约束优化直线的三维空间位置与相机位姿。3)利用CAPE[14]算法提取表面法向量,依据表面法向量估计环境中的曼哈顿主方向,然后关联关键帧与估计的曼哈顿主方向,并将其作为局部地图的约束优化相机位姿与地图。并在TUM RGB-D数据集上进行PLSC-SLAM 算法评估与对比实验。

1 PLSC-SLAM 算法总体框架

如图1所示,PLSC-SLAM 算法分为3个主线程:跟踪、局部地图、闭环检测。该算法是以ORBSLAM 框架为基础,基于环境中结构性约束设计的点线特征融合SLAM 算法。其中每个线程中的蓝色部分是PLSC-SLAM 所做的工作。

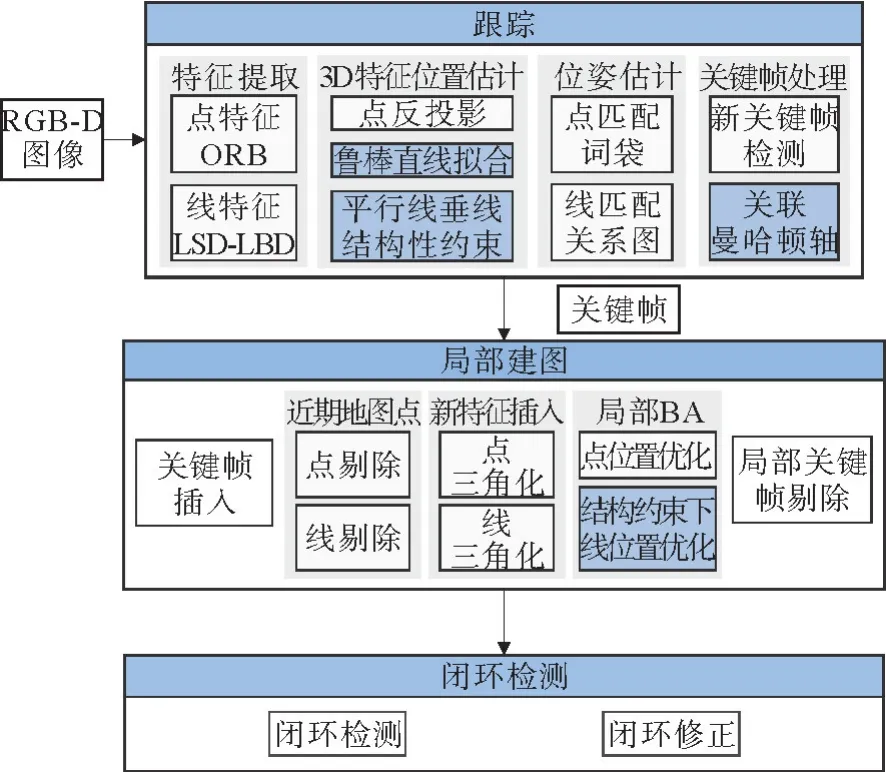
图1 PLSC-SLAM 算法框架Fig.1 Overview of PLSC-SLAM algorithm

跟踪线程对输入的每帧图像进行跟踪与处理,是SLAM 中的基本流程。跟踪的目的是提取当前帧的特征,建立当前帧与局部地图之间的共视关系及约束关系,用于优化当前帧的相机位姿。SLAM系统完成系统初始化后,对输入的当前帧图像提取点特征和线特征。在本阶段,使用ORB 算法提取和描述点特征,使用LSD 算法和LBD 描述符提取和描述线特征。利用三角化将点特征的三维位置恢复,然后将其映射到局部地图并进行匹配。对于线特征的三维位置,PLSC-SLAM 设计了平行线和垂直线分类算法,利用二者结构性约束优化线特征的三维位置。根据特征匹配关系,通过将当前帧的匹配特征投影到参考帧,利用非线性优化算法优化点线特征的投影误差即可得到当前相机位姿。判断当前帧是否符合关键帧选取条件,然后将满足条件的新关键帧关联曼哈顿主方向,最后将新关键帧保存到关键帧集合中。

局部地图线程对关键帧进行处理,目的是更新共视图与完成局部地图的构建。局部地图由共视关键帧和关键帧对应的地图点线构成。在该线程中,通过对新插入的关键帧计算,筛选关键帧和地图点线。然后进行局部BA(bundle adjustment,光束平差法)优化,同时优化相机位姿和地图点线。最后,对插入的关键帧和新的地图点线进行筛选,防止出现冗余关键帧。PLSC-SLAM 设计了一个曼哈顿主方向估计算法,利用曼哈顿约束优化关键帧的点线特征位置与相机位姿。

闭环检测线程分为闭环检测和闭环校正,主要用于消除估计的相机位姿和三角化后的地图点累积误差。闭环检测利用词袋模型检测关键帧数据库的相似程度来检测闭环。闭环校正包括闭环融合和图优化,将累计误差进一步消除。

2 结构性约束算法

2.1 垂线与平行线约束

在跟踪线程中,当特征点与特征线提取后,就可以获得它们在相机坐标系下的三维位置。对于一个特征点p i来说,通过对其进行三角化即可得到与二维特征点对应的三维地图点P ci。与特征点相比,特征线更容易受到深度不连续和遮挡的影响,通过对特征线进行三角化可能会导致特征线的三维位置不准确,因此使用RANSAC 拟合空间直线方法计算直线的三维位置。首先,统计与线段相交的深度值不为零的像素数量,如果这个数量超过某个阈值,就通过RANSAC算法估计三维线L ci并去除外点,具体流程如图2所示。

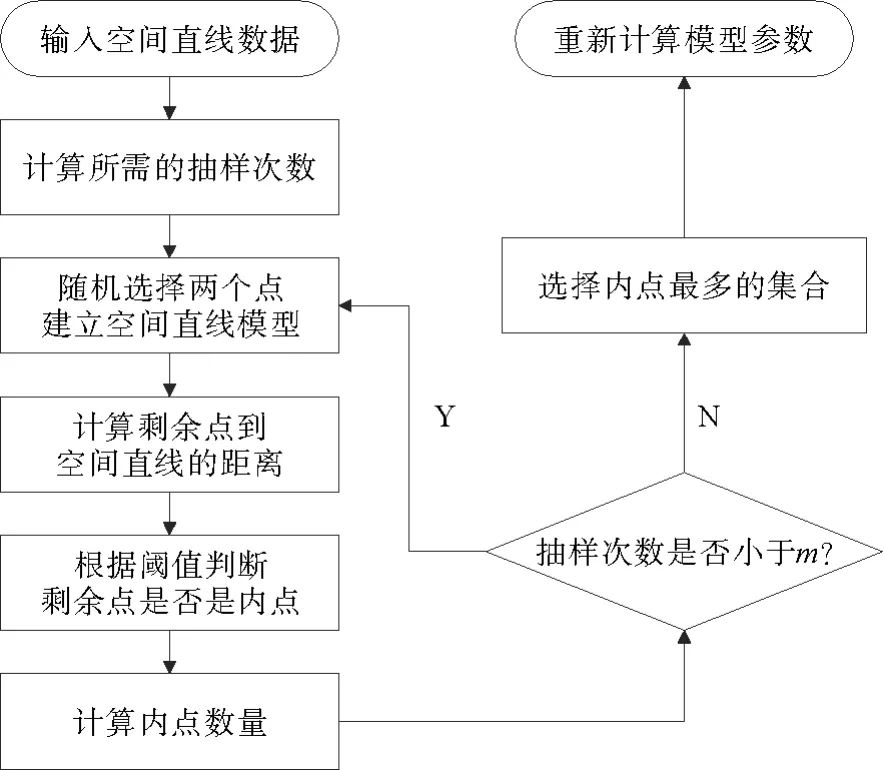
图2 RANSAC拟合空间直线流程图Fig.2 RANSAC fitting spatial line flow chart

然后,使用场景的结构性约束去优化每条检测的直线位置。对于当前图像中检测的每个可能的直线对,通过式(1)计算两个向量之间的夹角余弦值:

如图3所示,图中左图给出了相机坐标系中的特征点和特征线符号及其对应的三维点线符号,右图给出了垂线对误差和平行线对误差符号。

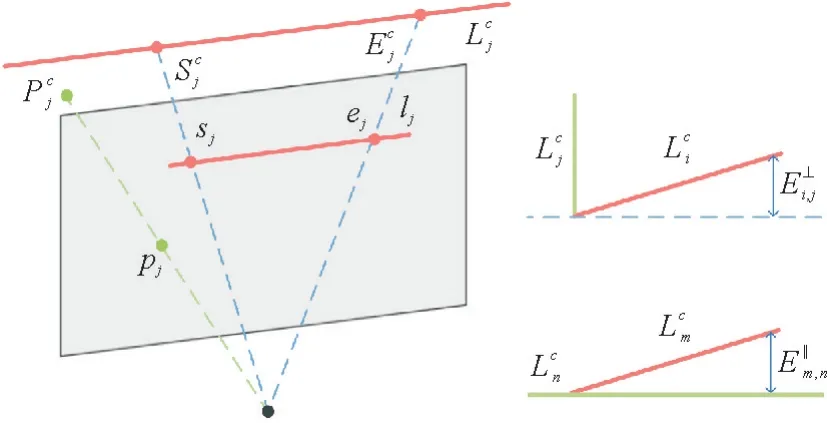
图3 点线二维三维位置示意图及垂线对、平行线对误差示意图Fig.3 Illustration of 2D and 3D position of point-line and illustration of perpendicular error and parallel error

定义L为待优化的变量集合,其中至少包含一种关联垂直与平行约束的线。然后,通过最小化以下误差函数来优化L的线端点位置:

其中ρ是用于减少外点影响的Huber核函数。

2.2 曼哈顿约束

如图4所示,曼哈顿世界假设假定环境中存在3个相互垂直主方向组成的坐标系O M,环境中存在的平面法向量与其中一个曼哈顿主方向一致。

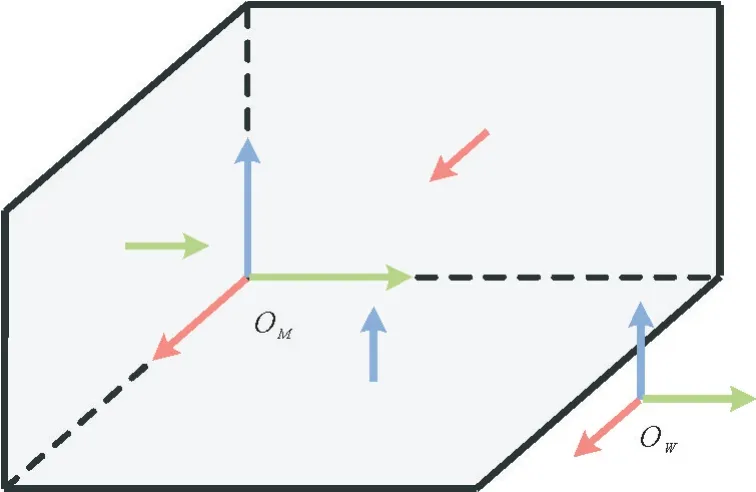
图4 曼哈顿世界假设示意图Fig.4 Illustration of Manhattan world hypothesis

2.2.1 表面法向量提取

表面法向量使用CAPE[14]算法提取,该算法首先将平面拟合到网格单元,然后通过在这些平面单元上进行区域生长来找到光滑的表面,最后将提取到的法向量表示为n=(n x n y nz)。CAPE 算法在不同场景延迟一致,速度更快。

为了便于将法向量可视化,用(n e+1)×255/2计算法向量对应的3通道像素值,把表面法向量转换成3通道图像。其中n e分别取n x、n y、n z,可视化后的表面法向量如图5所示。

图5 表面法向量可视化Fig.5 Visualization of surface normal vector

2.2.2 曼哈顿主方向估计

将曼哈顿世界坐标系(下文简写为MF)相对于相机坐标系的旋转关系用旋转矩阵Q·=[q1q2q3]表示,其中q1、q2、q3分别是曼哈顿坐标系的x、y、z轴在相机坐标系下的表示。通过式(6)将所有投影到MF的三轴切平面去计算均值偏移:

其中n i表示相机系下表面法向量,表示MF表面法向量,索引i j表示第i个主方向圆锥截面内的法向量。

使用黎曼对数映射表示切平面中的距离:

其中c表示高斯核宽度。使用黎曼指数将Mean-Shift算法结果转换回单位球面:

对MF所有轴重复以上过程,即可得到更新后的旋转矩阵:

使用Mean-Shift 聚类算法来初始化第一帧MF,从而使跟踪与局部地图建立在曼哈顿结构性约束框架下。

将与关键帧k有共视关系的关键帧记作Kco,被关键帧Kco观测到的地图点和地图线分别记作Pco和Lco,与关键帧k没有共视关系但观测到地图点Pco和地图线Lco的关键帧记作Knco。将Pco和Lco地图点线与关键帧k中特征之间的匹配关系分别记作匹配集ΩPk和ΩLk,与关键帧k有共视关系的垂线和平行线集合分别记作将Knco中与曼哈顿主方向有关联的地图线记作ΩM。定义优化变量,j∈Lco,l∈Kco},其中上标w表示世界坐标系。最后将优化问题定义为

其中K=Kco∩Knco,M j∈ΩM,E是误差。利用Levenberg-Marquardt算法对式(15)进行优化,即可得到优化后的点线三维位置和相机位姿。

3 实验结果及分析

3.1 评估标准与实验环境

为了验证提出的PLSC-SLAM 算法的有效性,在TUM RGB-D[16]数据集上评估了该算法的性能。TUM RGB-D数据集提供了几个图像序列,包括正常运动、快速运动、低纹理、无结构等特定场景。这些图像序列还具有通过外部运动捕捉系统获得的相机轨迹真值,可满足实验者不同的测试要求。

评价SLAM 算法精度指标常分为绝对轨迹误差(absolute pose error,APE)与相对轨迹误差[17](relative pose error,RPE)。绝对轨迹误差可以刻画SLAM 算法估计位姿与真实位姿的旋转和平移误差,能够反映系统精度与轨迹的一致性,故选取绝对轨迹误差APE 作为算法的精度评价指标。使用evo SLAM 评估工具,将提出的PLSC-SLAM 算法与多种不同视觉SLAM 算法进行比较。

所有实验均在一台装有Ubuntu 18.04 LTS操作系统的电脑上完成,12 GB RAM,处理器为Intel Core i5-7200U(2.50 GHz)。没有进行GPU 并行处理,以节省SLAM 算法运行成本。编程语言为C++、Python3,第三方库包括OpenCV 3.2、Eigen 3.1、G2O、Pangolin。

3.2 TUM RGB-D数据集定位结果与分析

PLSC-SLAM 对点线特征提取后,将提取的直线分为垂线与平行线,利用垂线与平行线的结构性约束优化地图线位置与相机位姿,避免了因点特征不足和线特征位置误差大导致定位失败及误差大的问题。fr1_room 图像序列沿着整个办公室墙壁走向拍摄,从4张桌子开始,然后围绕房间的墙壁运动,直到回到起点。该图像序列具有在墙壁、窗户上纹理稀疏,但墙角和窗户处存在垂直与平行的边缘直线的特点。图6、图7分别是PLSC-SLAM、ORBSLAM3在fr1_room 图像序列运行时的特征提取对比图与稀疏地图对比图。从图6(a)可以看出对图像进行点线特征提取后的结果,并且提取的直线存在明显的垂线与平行线。从图7(a)可以看到加入线特征后在局部地图中加入的地图线。

图6 特征提取对比Fig.6 Comparison of feature extraction

图7 地图对比Fig.7 Map comparison

如表1所示,选择了8组不同的TUM RGB-D图像序列进行实验测试。从命名能够看出这8组图像序列的特点,其中xyz表示相机平移运动,rpy表示相机做滚转、俯仰、偏航运动;desk、room 分别表示图像序列的采集环境在桌子周围和办公室内;str与nstr分别代表图像序列有无几何结构;tex与ntex分别表示图像序列有无纹理;near与far分别表示相机距离物体0.5和1 m。

表1 TUM RGB-D数据集上APE RMSE的评估结果Table 1 Evaluation results of APE RMSE on TUM RGB-D dataset/m

表1 分别给出了ORB-SLAM3、SP-SLAM、LSD-SLAM 及PLSC-SLAM 在8组图像序列测试的绝对轨迹误差结果。从结果可以看出,PLSCSLAM 获得的APE RMSE结果在不同程度上低于其他三种SLAM 算法。从表1可以看出在fr3_str_tex_far、fr3_str_tex_near两个具有结构性的RGBD数据集中,相比ORB-SLAM3,PLSC-SLAM 的精度分别提高了1.07%和20.30%,在剩余的多数数据集中,PLSC-SLAM 的定位精度都高于ORBSLAM3。而且PLSC-SLAM 在8组图像序列上都能稳定运行,完整估计相机轨迹,并没有出现跟踪丢失以及SLAM 算法定位失败的情况。

图8、图10 给出了PLSC-SLAM 与ORBSLAM3算法在fr1_room 图像序列上的APE 误差结果对比。从图中可以更直观地看出本工作PLSCSLAM 算法精度取得了显著的提高。究其原因,该算法对线特征三维位姿进行优化,提高当前帧与局部地图共视关键帧的匹配精度,降低了对相机位姿估计的误差。而加入结构性约束,依靠对曼哈顿主方向的估计,为后端优化提供了更多的约束条件,使得估计轨迹更接近真实轨迹。

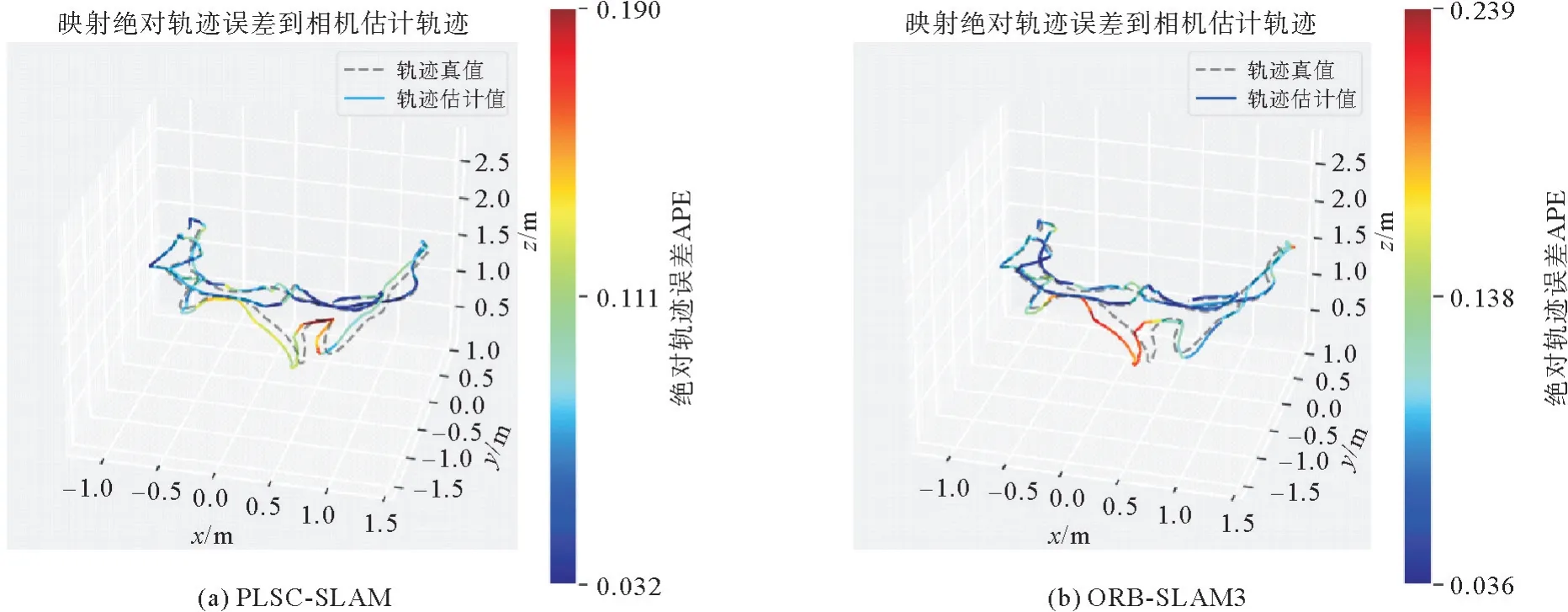
图8 fr1_room 数据集绝对轨迹误差在估计轨迹上的映射对比Fig.8 Comparison of absolute pose error mapped onto estimated trajectory of fr1_room dataset

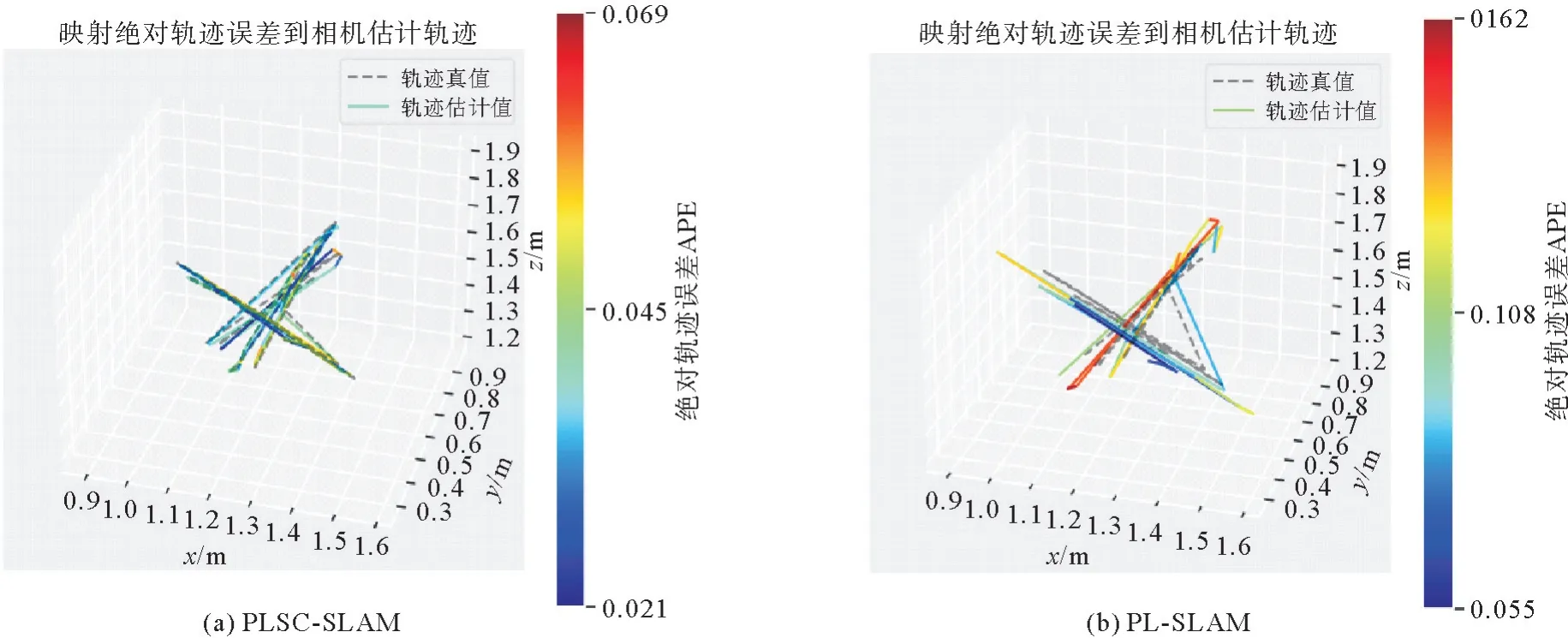
图9 fr1_xyz数据集绝对轨迹误差在估计轨迹上的映射对比Fig.9 Comparison of absolute pose error mapped onto estimated trajectory of fr1_xyz dataset

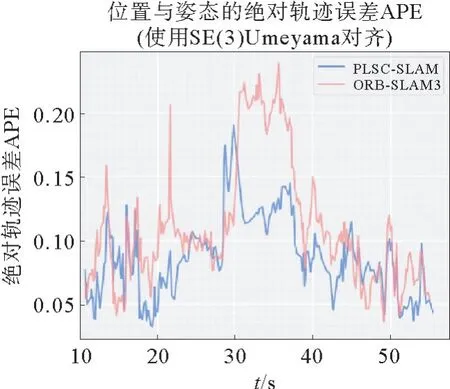
图10 PLSC-SLAM 与ORB-SLAM3在数据集fr1_room 上APE对比Fig.10 APE comparison between PLSC-SLAM and ORB-SLAM3 on fr1_room dataset

图9、图11是PLSC-SLAM 与PL-SLAM 算法在fr1_xyz图像序列上的APE 误差结果对比。两种算法都对点线特征进行提取,但PL-SLAM 没有利用环境中的结构性约束对跟踪过程的点线位置进行优化,也没有利用环境中的结构性约束优化局部地图,而PLSC-SLAM 充分考虑了环境中的结构性约束,并利用该约束优化相机位姿与局部地图。从二者对比结果可以看出,利用环境中的结构约束可以提高SLAM 系统的定位精度,减小估计轨迹与真实轨迹的误差。

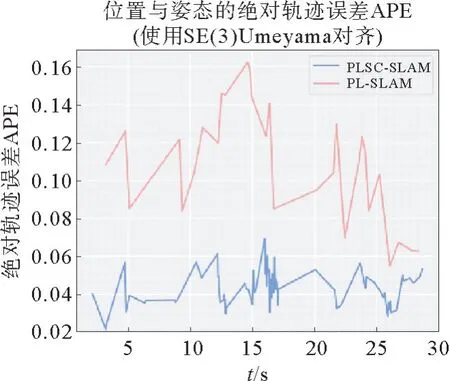
图11 PLSC-SLAM 与PL-SLAM 在数据集fr1_xyz上APE对比Fig.11 APE comparison between PLSC-SLAM and PL-SLAM on fr1_xyz dataset

4 结语

针对目前存在的稀疏特征点SLAM 算法在低纹理环境下难以提取足够多的特征点、定位精度低等问题,提出一种基于结构约束的点线特征融合PLSC-SLAM 算法。通过提取环境中的点线特征,充分利用环境中的结构性约束信息对直线三维位置与相机位姿进行优化,有效解决了点特征稀疏与定位精度低的问题。最后在TUM RGB-D 数据集上进行实验测试,依据绝对轨迹误差指标对本算法进行评估,结果表明本算法因加入线特征和结构性约束,提高了弱纹理环境中的定位精度与稳定性。