珠江三角洲网河区过江隧道极限冲刷深度研究

刘中峰，刘 达，罗志发，李 明，陈 晖

(1.广东省水利水电科学研究院，广州 510635；2.广东省水动力学应用研究重点实验室，广州 510635；3.河口水利技术国家地方联合工程实验室，广州 510635；4.广东省水安全科技协同创新中心，广州 510635)

1 概述

随着粤港澳大湾区世界级城市群建设的推进，珠三角各地之间互动性不断增强，高速公路等交通项目大量上马。珠三角水系发达，江河交错，公路跨江情况不可避免。因具有占地小、不影响通航等优势，过江隧道逐渐成为公路跨江的主要形式[1]。在设计过江隧道时，工程河段冲淤情况直接影响隧道工程建设方案，是确定隧道最大埋深的前提。埋深过小，虽可减少投资，但可能到最后隧道顶部出露，严重威胁工程安全；埋深过大，虽然工程安全可得以保障，但会增加工程投资及施工难度。因此，通过研究分析河床极限冲刷深度，合理、准确地确定既能保证安全又尽量减小投资的最大埋深，是过江隧道工程设计中必须解决的关键问题。众多学者都针对河床极限冲刷深度问题开展过研究[2-7]，研究手段主要有：河床演变分析、物理模型试验和数学模型计算。分析发现，既有文献大多采用单一研究手段，通过多种手段对该问题进行综合研究的情况相对较少。

本文在总结前人研究的基础上，以南沙明珠湾区跨江隧道工程为例，在河床演变分析的基础上，以物理模型试验为主，并辅以数学模型计算和经验公式计算两种手段，对隧道工程河段极限冲刷深度进行了研究。研究结果可为隧道工程埋深设计等提供重要依据，也可为完善此类问题的研究提供参考。

2 河道概况

拟建隧道工程横穿上横沥水道，该水道全长8.3 km，平均水面宽度约400 m，平均水深6.8 m，是珠三角网河区的重要通航河道和行洪排涝通道。该区水系洪水主要来自西江、北江和流溪河，具有明显的流域特征，洪水来源主要是暴雨。区域潮汐属不规则半日潮，日潮不等现象显著，潮位过程线表现为涨潮历时短，落潮历时长，呈不对称正弦曲线。受径流影响，年最高潮位多出现在汛期，尤其是夏季受热带气旋影响引发的风暴潮，常出现历史最高潮位，而年最低潮位则出现于枯水期；多年平均潮差在1.20～1.60 m之间，年内变化相对较大，年际变化不明显。根据已有资料，1999年7月、2001年2月、2008年8月及2012年8月上横沥水道中洪水期实测河床泥沙中值粒径依次为0.140 m、0.155 mm、0.072 mm和0.032 mm，总体上呈现泥沙粒径细化的趋势，这是河道比降减小、细颗粒泥沙落淤的表现。

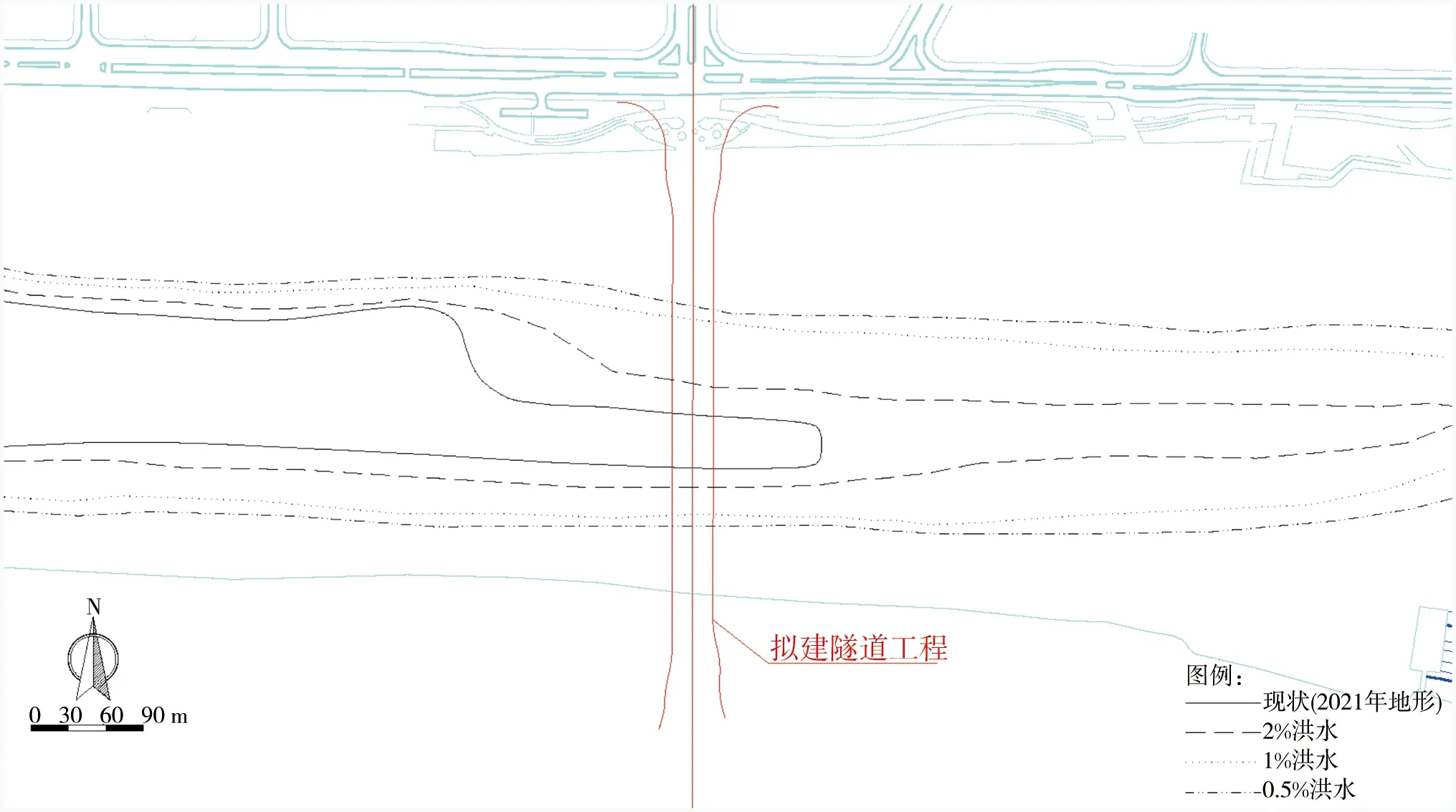
拟建南沙明珠湾区跨江隧道工程位于上横沥水道下游，上距已建凤凰二桥约1.0 km，下距河口(入汇蕉门水道)约1.5 km，跨江处水面宽度约为350 m(如图1所示)。

图1 工程河段河势及拟建隧道布置示意

3 工程河段近期河床演变特点

收集了工程河段1999年、2013年、2018年和2020年共4个年份的河道地形图，据其对比分析了该河段的主要冲淤变化情况：

1)从横向形态看，河道主槽横向位置基本稳定，河段平均宽度呈缩窄趋势，缩窄幅度为10.79～81.21 m；深泓线横向位置有一定的摆动，但摆幅较小，相对较稳定；断面过水面积有所减小，平均减小幅度约为65 m2。

2)从垂向高程看，该河段整体处于刷深下切状态，近20年来平均高程降低1.09 m，深泓高程平均降低1.77 m。

3)从河相系数看，总体呈减小趋势，减小幅度为-1.96～-1.16，平均减小1.53，河道河势相对不稳定；从河段容积变化看，1999—2013年、2013—2018年和2018—2020年年均冲淤量分别为14.99×104 m3/a、14.93×104 m3/a和22.93×104 m3/a。

总体而言，工程河段平面形态较为稳定，河道水深有逐年增加趋势，河道整体呈一定的下切趋势，但基本处于相对稳定状态。

4 物理模型

4.1 模型概况

依据相关技术规范[8-9]，根据工程河段地形、水沙特征及试验场地等条件，建立上横沥水道进出口之间约4.9 km河段的正态模型，模型几何比尺为1∶80。模型制作分为两个阶段，首先制作定床模型，用于模型率定与工程前的流态、流速分析；其次将拟定的铺沙范围(拟建隧道上下游各1 km范围)制作成动床，用于极限冲刷试验(如图2所示)。

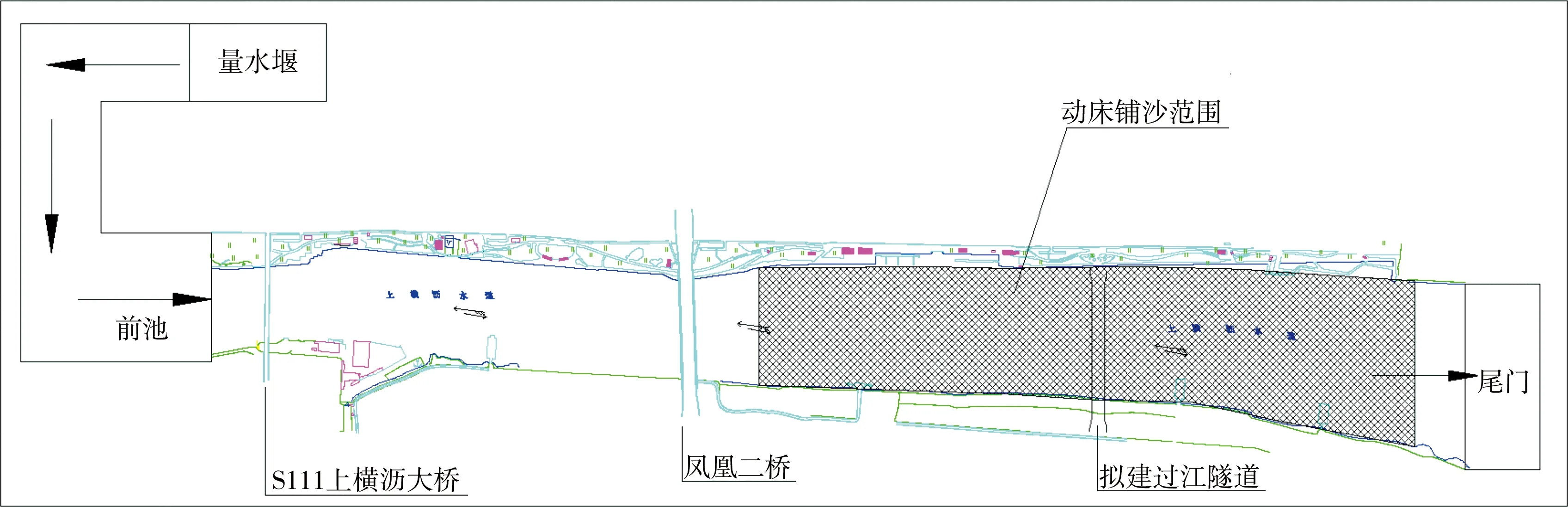
图2 物理模型布置概化示意

4.2 模型选沙

工程附近区域的表层河床泥沙以淤泥为主，前述分析显示河床沙粒径具有细化的趋势。结合已有实测资料并偏于安全考虑，本次试验泥沙中值粒径取0.04 mm。

根据以往试验经验，本次研究选取性能稳定，粒径变化范围大，且在动床模型中常用的塑料沙作为模型沙。经反复计算和配制，并根据水槽起动流速试验成果(见表1)，s=1.25 t/m3、d50=0.21 mm的塑料沙在模型水深为0.100～0.188 m(相当于原型水深为8～15 m)时，其起动流速为0.076～0.083 m/s，相应的起动流速比尺为10.20～10.58(平均值为10.27)，与理论流速比尺8.94相近(大于理论流速比尺，偏安全)，满足起动相似要求。

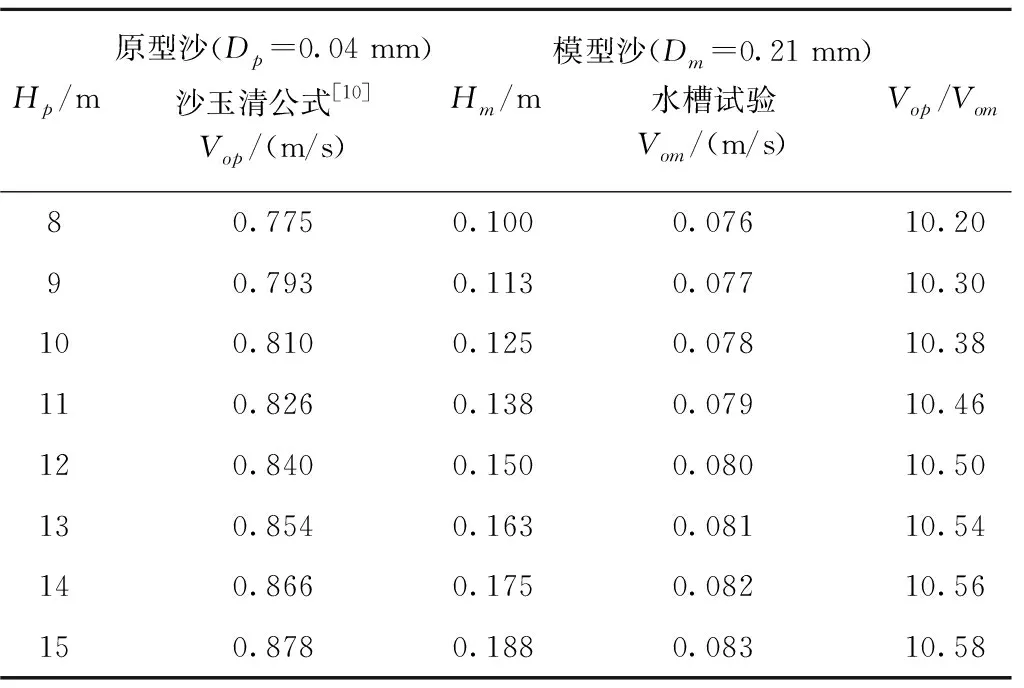
表1 不同水位下天然砂起动流速

4.3 模型验证

4.3.1定床模型验证

采用恒定流对定床模型进行验证，选定3个典型水文条件作为验证组次(见表2)，比对依据选取已经实测数据率定验证的数学模型的相应计算结果。受篇幅限制，本文仅给出验证结论：从水位看，物理模型的沿程水位和数模计算水位基本吻合，水位误差一般在±5 cm以内，表明模型和原体的阻力达到较好的相似；由流速分布，除各断面两端采样点的流速相对误差较大外(其主要原因在于两种模拟手段对滩地处理有所差别)，其余采样点物理模型试验结果与数模计算结果吻合较好(相对误差在±10%以内)，流速大小变化规律大致相同，基本满足规程规范对流速偏差的精度要求。

表2 模型(验证)试验组次

模型率定验证结果表明，模拟水流的水面线、流速与数学模型(已经实测数据验证)计算结果基本吻合，模拟水流运动满足了与实际水流特征相似的要求，较好地反映了拟建隧道工程附近水域的水流运动规律，该模型进一步用于动床极限冲刷试验是合理的。

4.3.2动床相似性说明

考虑工程河道人类活动较多，人为影响因素较大，地形测量相邻年份较远，实测地形资料可用性较差，因此本次动床模型试验未进行冲刷验证。动床相似性主要作如下考虑：

1)动床采用规范公式计算来确定各类比尺。

2)在模型控制上，动床模型与定床验证试验水流控制条件相同。

3)合理选择模型沙，本次试验进行了模型沙的起动流速水槽试验，模型选用模型沙的特性与原型沙在起动相似较为一致。

综上，可认为本次动床模型基本满足河床变形相似要求[11-12]。

5 河床冲刷深度分析

5.1 试验水文条件及试验控制

动床模型试验研究主要关注的是河道极限冲刷引起河床下切对工程安全的影响，而河道极限冲刷是发生在最不利的洪潮组合条件下，因此物理模型试验时应选取不利的洪水水文组合。经分析，模型选取上游频率洪水遭遇下游河口“2005.6”洪水潮型低潮位为最不利的水文组合。据此，物模试验组次与验证试验组次保持一致，具体见表2所示。

在上述各水文组次下，采用清水动床模型开展极端冲刷试验。在流量、水位稳定后，分别进行冲刷时间为3 h和4 h的动床试验(模型时间)，观测到，与冲刷3 h的河床地形相比，冲刷4 h后河床基本无变化。这表明试验3 h后，河床冲刷已基本稳定，因此，选定3 h(约相当于原型27 h)作为此次极限冲刷试验的控制时间。

5.2 试验成果

图3为200 a一遇洪水条件下拟建工程附近河段底流速分布情况。可见，该河段最大底流速在1.40 m/s左右。由4.2已知，该河段河床为较易起动的淤泥、粉细砂，起动流速在0.8 m/s左右。故当遭遇试验工况大洪水时，河道底流速远大于床沙起动流速，河床将出现一定程度的冲刷，且冲刷幅度随流量增加而增大。

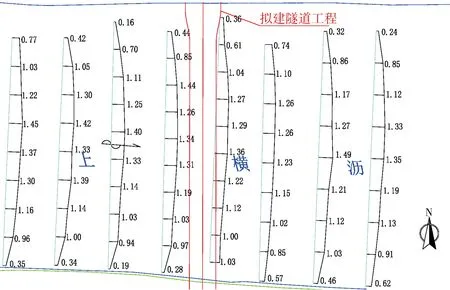
图3 底流速分布示意(0.5%)(单位：m/s)

在水流冲刷作用下，床沙出现鱼鳞状沙波，以波峰、波谷高程的均值作为标准，测定了不同组次下的等高线情况(见图4)。可以看出，跟初始地形相比，冲刷后河道等高线总体趋势表现为向两岸扩散，各等高线向两岸退缩幅度基本在50 m以内；同时，现状未贯通的-9 m和-10 m等高线都向下游有所延伸，且在0.5%组次均得以上下贯通。

a -9 m等高线

b -10 m等高线图4 等高线对比示意

图5为不同试验工况下深泓线的位置，从图中可以看出，不论是与初始地形相比，还是各试验组次之间相比，隧址上下游附近河段深泓位置变化不大，仅局部有一定幅度的摆动，大部分河段的深泓线左右摆幅基本在30 m以内。其中，隧址断面深泓线略向河道左岸侧偏移，最大偏移距离为23 m(P=0.5%)。在隧址下游约350 m处摆幅较大，深泓线由右向左摆动，最大摆幅在50 m左右(P=1%)。

图5 深泓线位置对比示意

图6为拟建隧道工程所在断面冲淤变化情况，表3统计了该断面冲淤变化特征值。由图6和表3可以看出，该断面形态变化不大，基本保持为“U”型河槽，但断面主槽出现一定程度的冲刷，且随着上游来水的增加，冲刷程度越大。P=0.5%组次下，工程所在断面河床最大冲刷深度为2.97 m，对应河床高程为-5.49 m，距离左岸约49 m；该断面冲刷后河床最低高程为-11.68 m，对应冲刷深度为1.86 m，距离左岸约221 m。

图6 拟建工程断面河床冲淤变化示意

表3 拟建工程断面冲刷特征值统计 m

5.3 试验成果合理性分析

为论证物理模型试验成果的合理性，分别采用数学模型和经验公式法，在同样边界条件下对最大冲刷深度进行了计算。其中，数学模型为二维潮流悬沙输运模型，其悬沙输移方程及河床冲淤变形方程参见文献[13]；经验公式采用《河道管理范围内建设项目技术规程》[14]中粘性土河床的河槽一般冲刷公式。

图7为200 a一遇洪水条件下拟建工程断面极限冲刷的3种方法研究结果对比。从最大冲深看，数学模型计算的最大冲深为2.77 m，稍小于物理模型测得的2.97 m，出现位置相差不大；从冲刷后的最低标高看，数学模型计算结果为-11.59 m，经验公式计算结果为-11.43 m，均略高于物理模型测得的-11.68 m。总体看，3种方法得到的冲刷后地形最低标高成果相差不大，表明物理模型试验成果较为合理且偏于工程安全。

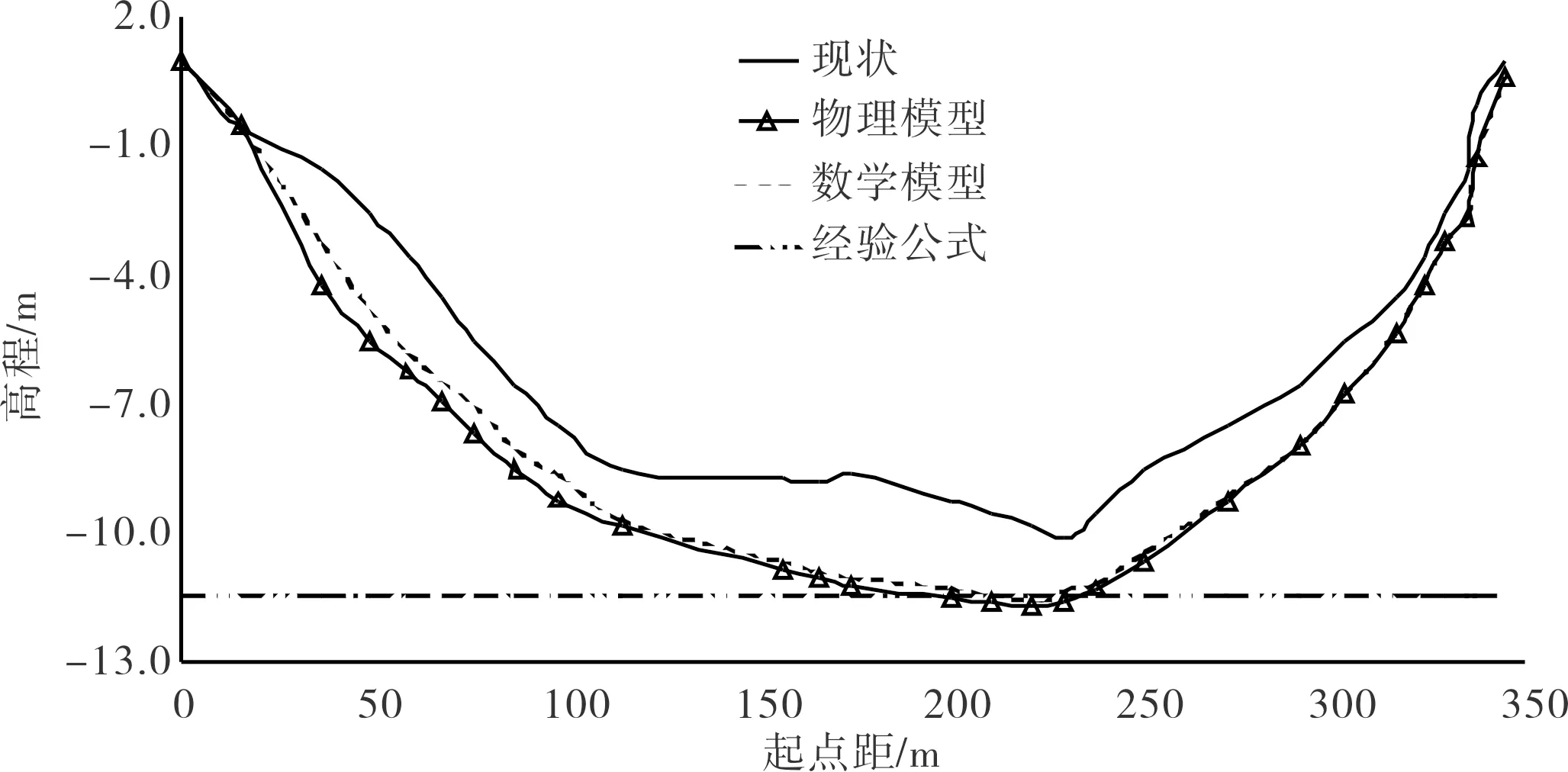
图7 拟建工程断面极限冲刷不同方法研究结果对比示意(P=0.5%)

6 结论及建议

1)在河床演变基础上，以清水动床物理模型试验为主要手段对南沙明珠湾区跨江隧道工程所在位置开展了极限冲刷研究，通过模型率定验证和合理选沙，模型基本满足规程规范要求，可用来模拟工程区域的水动力及极限冲刷情况。

2)试验结果表明，发生试验洪水时，河道底流速远大于床沙起动流速，河床将出现一定程度的冲刷，且冲刷幅度随流量增加而增大，200 a一遇洪水下，隧址所在断面最大冲刷深度为2.97 m，冲刷后河床最低高程为-11.68 m。

3)将物理模型试验成果与数学模型和经验公式的计算成果进行了对比分析，结果显示3种方法确定的极限冲刷成果较为接近，表明物理模型试验成果合理可信且偏于安全，可为确定隧道埋深提供参考依据。

4)需要指出的是，本文试验主要考虑了床沙中值粒径这一参数，并假定粒径保持不变，忽略了床沙的不均匀组成和冲刷过程中的粒径变化等。今后工作中，建议加强对工程河段泥沙特性和河床冲淤变化的观测和资料积累，以便对极限冲刷深度确定这一工程难题进行更深入的研究。