Auto CAD 图解法在缓和曲线计算中的应用

刘建利

（辽宁省交通高等专科学校， 辽宁 沈阳 110122）

1 Auto CAD 图解法计算缓和曲线坐标概述

采用Auto CAD 图解法计算缓和曲线坐标，首先需建立合理的直角坐标系， 并设置好距离、角度单位及显示精度； 然后依据工程设计提供的各项要素数据， 正确绘制出道路平面曲线路线图， 最后通过Auto CAD 的图形属性查询工具，获得施工测量所需的各项坐标数据及曲线要素数据。 由于缓和曲线是用Auto CAD 中多段较短直线拟合形成的， 为确保所绘缓和曲线各拟合点的坐标具有较高的精度， 根据缓和曲线长度和曲率半径， 选择合理的步长来拟合缓和曲线。

2 缓和曲线及基本计算公式

缓和曲线是在直线与圆曲线之间或两条相同转向的不同半径圆曲线之间起缓和与过渡作用的曲线。 为了保证行车的安全与平顺， 要求不同线型曲线连接处必须平稳地过渡， 以缓和曲线连接直线和圆曲线为例， 在HY、 YH 点处必须满足缓和曲线的半径和圆曲线的半径相等， 并且缓和曲线和圆曲线在HY、 YH 点的切线也必须重合。

目前我国公路和铁路系统中， 一般多采用回旋线作为缓和曲线。 回旋线是曲率半径随曲线长度的增大而成反比均匀减小的曲线， 即回旋线上任一点的曲率半径与曲线的长度的乘积为定值。以公式（1） 表示：

式中：l为回旋线上某点到回旋线起点 （r=∞） 的曲线长；R为缓和曲线某点的曲率半径；A为缓和曲线参数， 表示缓和曲线曲率变化的缓急程度。

直角坐标系下的缓和曲线坐标如图1 所示，以缓和曲线起点 （x=∞） 为坐标原点， 以缓和曲线起点（x=∞） 切线方向为X 轴方向， 通过原点的缓和曲线半径方向为Y 轴方向， 缓和曲线直角坐标公式实际上是无穷级数的展开式， 其中A越小， 缓和曲线l越长， 要求取位就越多。 实际工程中X 坐标一般取前四项， Y 坐标取前三项即能满足精度要求。

图1 缓和曲线直角坐标

式中：x为缓和曲线横坐标；y为缓和曲线纵坐标。

缓和曲线上任意一点P的切线与X轴的夹角β 称为该点的切线角， 该角值与P点至缓和曲线起点ZH （HZ） 的曲线长所对的中心角相等。

式中： β 为缓和曲线切线角。

3 缓和曲线图解法计算坐标实例

如图2 所示已知某道路曲线第一切线上控制点ZD1 （x=4637516.318， y=542398.463） 和JD1（x=4637998.246， y=542001.178）， 该曲线设计半径R=1200m， 缓和曲线长L=110m， JD1 里程为K1+500， 转向角=30°32′18″。 计算出道路曲线主点ZH、 HY、 QZ、 YH、 HZ 点坐标， 及第一缓和曲线和圆曲线上的中桩点 （K1+220、 K1+250）坐标。

图2 缓和曲线线路图

3.1 利用Excel 计算出缓和曲线直角坐标

Excel 中单元格的引用分为绝对引用、 相对引用， 绝对引用和相对引用的区别在于拖动单元格复制公式时处理的数据是原来的数据还是新的数据， 在默认状态下， Excel 进行数据处理时都是相对引用， 相对引用公式中的每个相对引用单元格在公式被沿列或跨行复制时都自动改变； 要采用绝对引用需在单元格前面加 “＄”， 绝对引用公式中的每个相对引用单元格在公式被沿列或跨行复制时都不会改变。

由于Auto CAD 中没有缓和曲线的绘制工具，一般可以采用直线拟合出缓和曲线， 这样首先需要选择合适的步长， 然后分段计算出缓和曲线的直角坐标。 计算缓和曲线坐标可以利用Excel 的公式复制功能， 在Excel 中首行输入缓和曲线直角坐标计算公式， 在设置好单元格的相对引用或绝对引用后， 再用鼠标向下拖拽单元格即可计算出其他行坐标。 如下表1 所示： 缓和曲线步长为4 米， 分段计算出缓和曲线的直角坐标， 为了验证直线拟合缓和曲线的精度， 需要计算出每段直线的长度之和， 再同缓和曲线的设计长度进行比较。 通过Excel 计算出的所有直线段长度和为109.999984 米， 缓和曲线的设计长度为110 米，两者差值仅为0.016 毫米， 可以满足工程的精度要求。

表1 缓和曲线直角坐标计算

表2 缓和曲线成果表

直线拟合总长度满足要求后， 还需要计算出缓和曲线点的最大拟合偏差， 由于采用了直线拟合缓和曲线， 曲率半径越小， 则曲线与直线的偏差就越大， 缓和曲线的曲率半径随着曲线的长度增大， 而越来越小， 所以可以采用本缓和曲线的最小处的曲率半径来进行计算。 如下图3 所示计算出D 的距离， D=1.67 毫米。 直线拟合最大偏差为1.67 毫米， 一般可以满足工程精度要求。

图3 直线拟合曲线精度分析图

3.2 建立测量坐标系与绘制拟合的缓和曲线

Auto CAD 中包括两种坐标系统， 世界坐标系和用户坐标系。 世界坐标系是Auto CAD 默认的坐标系中， 水平向右为X 轴正方向， 竖直向上是Y 轴正方向， 垂直屏幕指向用户方向为Z 轴正方向。 用户坐标系可以自定义原点的位置和X、Y 轴的指向， 本文定义的用户坐标系如图4 所示。

图4 建立缓和曲线直角坐标系

如图4 所示首先在Auto CAD 中给制出ZD1和JD1 两个点， 绘制时需注意先输入横坐标 （Y坐标）、 后输入纵坐标 （X 坐标）， 然后将此两点连接成一条直线。

为了实现测量Auto CAD 坐标系与缓和曲线坐标系的一致性， 需要利用Auto CAD 中的自定义坐标系功能定义新的用户坐标系。 自定义用户坐标系建立要求如图4 所示： ZD1 为坐标原点；切线方为X 轴正方向， X 轴顺时针旋转90°为Y轴正方向。 坐标系定义完之后， 可以把如表1 所示的缓和曲线直角坐标复制粘贴到记事本上， 格式为： “X 坐标” “逗号” “Y 坐标”， 然后执行Auto CAD 中的 “多段线” 命令， 在命令窗口粘贴上所有的缓和曲线直角坐标， 如图5 所示即可绘制出拟合的缓和曲线。

图5 绘制缓和曲线

3.3 绘制圆曲线圆心与辅助线

缓和曲线绘制完成后， 需绘制出HY 点的切线， 首先根据公式4 计算出HY 点的切线角（2°37′33.8″）， 利用旋转和平移工具， 绘出过HY的切线。 切线完成绘制后， 需绘制出圆曲线， 其步骤如下：

（1） 在HY 点处绘制出同切线的相垂直的直线

（2） 沿垂线方向量取距离1200 米， 绘制出圆心O 点

（3） 可通过 “圆心、 起点、 角度” 工具， 绘制出如图6 所示的圆曲线， 圆曲线可以绘制的较长一些， 即圆心角可以取值大一些

图6 绘制圆曲线

圆曲线绘制完成后， 需绘制出切线方向的角平分线， 如图7 所示过JD1 绘制出两条切线的角平分线， 然后过O 点绘制出第一切线 （ZD1—JD1） 的平行线， 与角平分线 （JD1—P 方向） 相交于P 点。

图7 绘制辅助线

3.4 平移曲线

依据道路曲线特性可知， 如图8 所示圆曲线的圆心点一定在切线角的角平分线上（JD1—P 方向）， 所以需沿切线方向移动曲线， 这时只要圆曲线圆心在角平分线上即可， 然后绘制出完整的曲线， 其步骤如下：

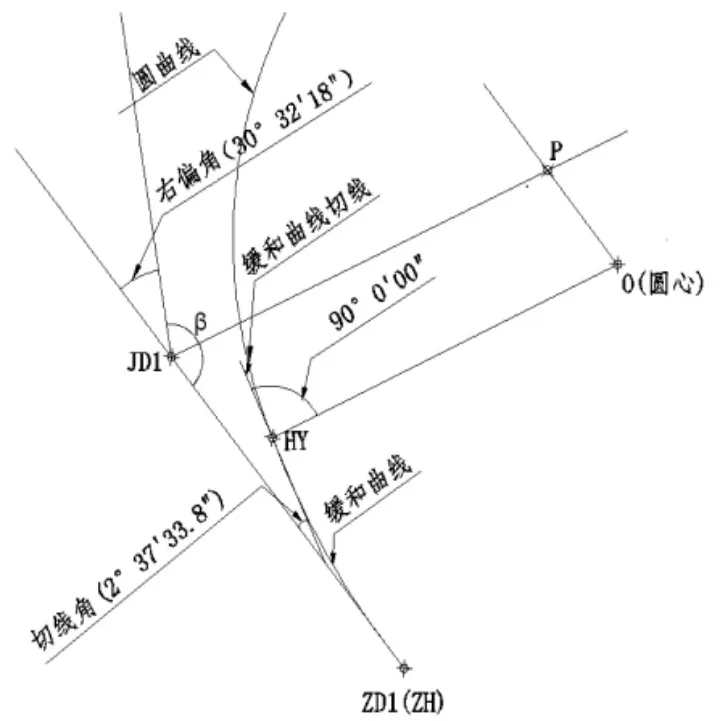
图8 平移曲线

（1） 利用平移工具将曲线进行平移， 平移时基点选择O 点， 移动点拾取p 点即可。

（2） 然后利用修剪工具进行修剪， （保留ZH—HY—QZ 曲线部分）， 其余部分删除。

（3） 最后用镜像工具绘制出YH—HZ 部分。最终的缓和曲线如图9 所示。

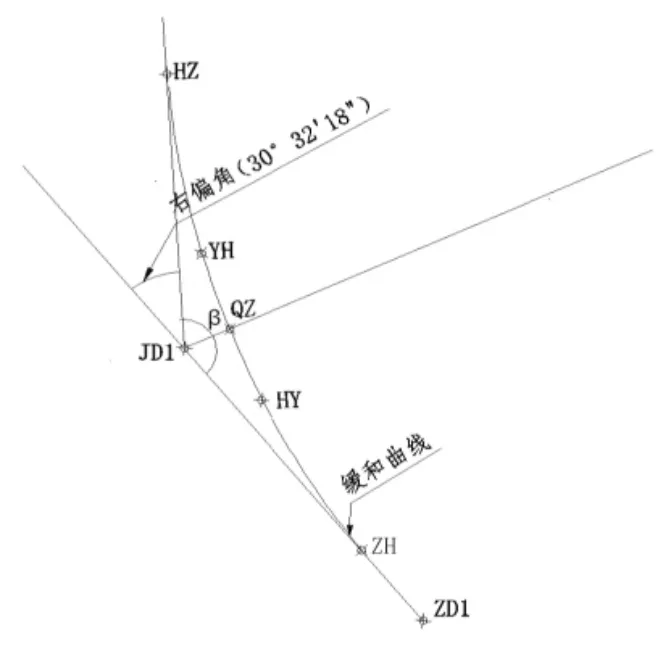
图9 镜像曲线

3.5 验证平移曲线的正确性与坐标查询

在图解完成缓和曲线后， 需验证下曲线的正确性与精度， 一般可以先在图面上查询出曲线长（749.593）、 切线长 （382.700）、 外距 （44.346）等曲线要素， 然后再依据相关计算公式计算出这些要素， 进行比较， 一般小于1 毫米即可。

在完成上述工作后， 需要将Auto CAD 的坐标系统恢复成默认的坐标系统， 即世界坐标系，然后通过查询工具可以查询出5 个主点 （ZH、HY、 QZ、 YH、 HZ） 坐标， 注意查询出的横坐标是Y 坐标， 纵坐标是X 坐标， 即是将Auto CAD 直接查询出的X、 Y 坐标需要相互调换下。

查询K1+220 及K1＋250 坐标方法如下：

（1） 将圆曲线及缓和曲线通过多段线连接工具将其连接成一条整体的多段线（ZHUKOV）

（2） 根据JD1 的里程 （K1+500） 和切线长（382.700）， 计算出ZH 点里程（K1+ 117.300）

（3） 计算出K1＋220、 K1＋250 到ZH 点的曲线长度

（4） 通过Auto CAD 定距等分绘点， 输入距离（K1＋220、 K1＋250 到ZH 的曲线长度），

鼠标拾取曲线的靠近ZH 点附近， 绘制出最近的点即为K1＋220 （K1＋250）。

（5） 通过查询工具查询点的坐标。

4 结束语

Auto CAD 图解法可以应用于工程中的坐标计算工作， 根据给定的坐标、 角度、 距离、 线切、 垂直等几何关系绘制出工程图， 然后可以直观地看出各个测量点的关系与实际是否相符， 在具体操作过程中， 要注意正确使用Auto CAD 精确捕捉的功能， 否则查询的坐标会有误差， 同时需要注意Auto CAD 坐标系和测量坐标系的定义不同， 需要将测量坐标系中的横、 纵坐标互换（或定义用户坐标系） 后再进行图解计算， 否则图解出的图形， 同实际图形之间的相对位置关系将不正确， 从而容易导致判断错误。