自抗扰和新型滑模观测器的PMSM无传感器控制
高俊岭,黄豪磊,张 磊,田 琳
(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)凭借高效率、结构简易等优势,在电动汽车、风机等领域获得了广泛应用[1].传统PMSM普遍采用机械式传感器对转子信息进行检测,这种检测方法存在电机体积大、可靠性低等缺点,无传感器控制很好地解决了这些问题,诸多学者也一直致力于该领域的研究[2].目前,中高速无传感器控制主要有扩展卡尔曼滤波(EKF)[3]、滑模观测器(SMO)[4]和模型参考自适应(MRAS)[5]等方法.
滑模观测器(Sliding Mode Observer,SMO)法是一种使用非常广泛的控制策略,由于滑模控制器自身机制会引起严重的系统抖振,文献[6]采用分段指数型函数作为滑模切换函数,有效削弱了滑模抖振,提高了系统的电流响应,但低通滤波器的使用使相位存在一定的滞后性.文献[7]采用高阶滑模观测器观测转子信息,应用新型滑模控制器作为速度控制器,有效降低了系统抖振,获得了良好的控制效果,由于系统转速存在较大的超调量,导致转速估计精度不高.文献[8]设计了一种双滑模控制策略,对滑模速度控制器和观测器都进行了优化,有效缩短了系统的响应时间,降低了系统抖振,但该方法在一定程度上增加了系统的运算量.
本文以id=0的PMSM矢量控制系统为研究对象,速度环采用自抗扰控制器(Active Disturbance Dejection Controller, ADRC)提高了系统的动态响应速度,增强了系统的抗扰能力.在满足Lyapunov稳定性的条件下设计新型滑模观测器(New Sliding Mode Observer, NSMO),从切换函数的角度降低了系统抖振,同时设计了一种可变边界层正弦输入函数;利用反电动势观测器对等效反电动势进行处理,有效避免了低通滤波器的使用及相位补偿问题.
1 自抗扰速度控制器设计
1.1 永磁同步电机的数学模型
表贴式PMSM在d、q坐标系下的数学模型为:
(1)
式中:ud、uq为定子电压d、q轴分量;id、iq为定子电流d、q轴分量;Ls为定子电感;φf为转子永磁体磁链;J为转动惯量;Te为电磁转矩;φd、φq分别为磁链的d、q轴分量;TL为负载转矩;Pn为极对数;Bω为摩擦系数;ωr为转子角速度;iq为交轴电流;R为定子电阻.
1.2 速度环ADRC设计
自抗扰控制主要包括跟踪微分器(TD)、扩张状态观测器(ESO)和非线性误差反馈控制率(NLSEF).为了减少计算量,速度环采用一阶ADRC.
TD:
(2)
ESO:
(3)
NLSEF:
(4)
以上公式中:e1、e2、e3为误差信号;α1、α21、α22、α3为跟踪因子;δ1、δ21、δ22、δ3为滤波因子;w*为TD的输入信号;z11为w*的跟踪信号;r0为TD的速度因子;β1、β2为ESO输出误差校正增益;ω为输出信号;z21为ESO观测输出速度;z22为扰动观测量;u0为NLSEF输出控制信号;k为调节器增益;b为补偿因子;u是补偿后的输入信号;fal代表非线性函数,其表达式为:
(5)
式中:sgn为符号函数.
2 新型滑模观测器设计
式(1)中d、q坐标下的电流方程经反Park变换得到α、β静止坐标下的电流方程为:
(6)
式中:iα、iβ为定子电流;uα、uβ为定子电压;θ为转子位置角;eα、eβ表示扩展反电势.
由定子电流误差构建新型滑模观测器的结构模型如图1所示.
2.1 新型滑模观测器
利用电流误差构造滑模面为:
(7)

图1 新型滑模观测器结构

不同滑模函数设计的滑模观测器具有不同的观测效果,传统滑模观测器通常采用开关函数作为滑模切换函数,而开关函数存在严重的滑模抖振.为了减弱系统抖振,文献[9]采用边界层固定不变的饱和函数作为滑模函数,但固定边界层厚度会影响系统的收敛速度.因此,采用边界层随转速可调的正弦输入函数F(s)作为切换函数,用来削弱滑模抖振和满足高性能控制的需要,其表达式为:
(8)
式中:m为边界层厚度(正常数);s为滑模面函数.
F(s)的函数曲线如图2所示.图2中,F(s)在整个实数域内连续且在零点处的函数值为零,常数m可以调节F(s)的陡度.边界层厚度m1、m2、m3分别对应转速ω1、ω2、ω3.速度较高时,通常采用较小的边界层m,此时对系统抖振的抑制较强,同理低速系统通常采用较大的边界层.因此,不同转速下的m值可通过查表法获得.

图2 F(s)函数曲线
边界层厚度m通过经验获得,在满足系统收敛性的同时要尽可能小[10].以300 r/min~1000 r/min转速范围为例,将这一范围划分为4个区间,不同区间的边界层m如表1所列.本文取m=0.2,重新定义了边界层厚度.

表1 不同转速下边界层厚度
新型滑模观测器的模型设计为:
(9)
式中:K为常数,表示滑模增益.
式(9)减去式(6)即可得到电流误差方程为:
(10)
将式(10)简化为:
(11)
式中:


为了保证系统稳定,构造Lyapunov函数为:
(12)
(13)

2.2 反电动势观测器
传统滑模观测器由于低通滤波器的使用会给系统带来相位延迟,且延迟角度的大小与电机实际转速及低通滤波器截止频率有关,估计精度较差.设计反电动势观测器不仅能够避免低通滤波器的使用和由此产生的相位补偿问题,简化系统,而且有效提高了转子位置和速度的估计精度.PMSM的反电动势模型可表示为:
(14)
由反电动势模型可以得到反电动势观测器设计方程为:
(15)

(16)

通过分析观测器的稳定性,定义Lyapunov函数为:
(17)
对式(17)求微分可得:
(18)
将式(16)代入式(18),得:
(19)

3 仿真实验与结果分析
在Matlab/Simulink中搭建自抗扰和新型滑模观测器的PMSM控制系统仿真模型.系统整体框架如图3所示.

图3 自抗扰和新型滑模观测器的PMSM系统框架
通过与传统滑模控制器(Sliding Mode Controller,SMC)和观测器相结合的控制方法进行对比,验证自抗扰和新型滑模观测器的优越性.仿真所用的PMSM主要电气参数如表2所列.

表2 永磁同步电机主要参数
3.1 加速和抗扰性能分析
ADRC和SMC控制方法下的实际转速波形如图4所示.

图4 ADRC和SMC实际转速波形
由图4可知,与传统滑模控制器相比,自抗扰控制器在电机启动和突加转速时能够快速稳定于给定转速,响应速度更快,转速抖振几乎为零.在0.08 s突加5 N·m负载时,传统滑模控制器的转速降落达到了95 r/min,恢复给定转速所需时间较长;而自抗扰控制器的转速降落仅为8 r/min,转速波动较小.结果表明自抗扰控制器具有较好的动态性能和抗干扰能力.
两种控制方法下的转速误差如图5所示.由图5可知,传统滑模观测器初始启动阶段的转速误差达到了10 r/min,当转速增加至1 000 r/min时,误差在-2~4 r/min之间波动,且突加转速或突加负载时误差都发生了较大波动;而新型滑模观测器在启动阶段的转速误差最大仅为0.12 r/min,当转速增加至1 000 r/min时,误差在0.02~0.1 r/min之间波动,有效减小了转子转速的估计误差.

图5 实际转速与估计转速误差
3.2 观测器性能分析
两种控制方法下的转子实际角度与观测角度曲线如图6所示.由图6可知,新型滑模观测器的转子位置跟踪效果明显优于传统滑模观测器.

图6 滑模观测器实际角度与观测角度
当转速为500 r/min时,传统滑模和新型滑模观测器的转子位置估计误差比较曲线如图7所示.由图7可知,传统滑模观测器得到的位置估计误差达到了0.026 rad,并伴有高频抖振;而改进滑模观测器的位置估计误差仅为0.0 105 rad,有效削弱了抖振幅值并减小了转子位置估计误差.
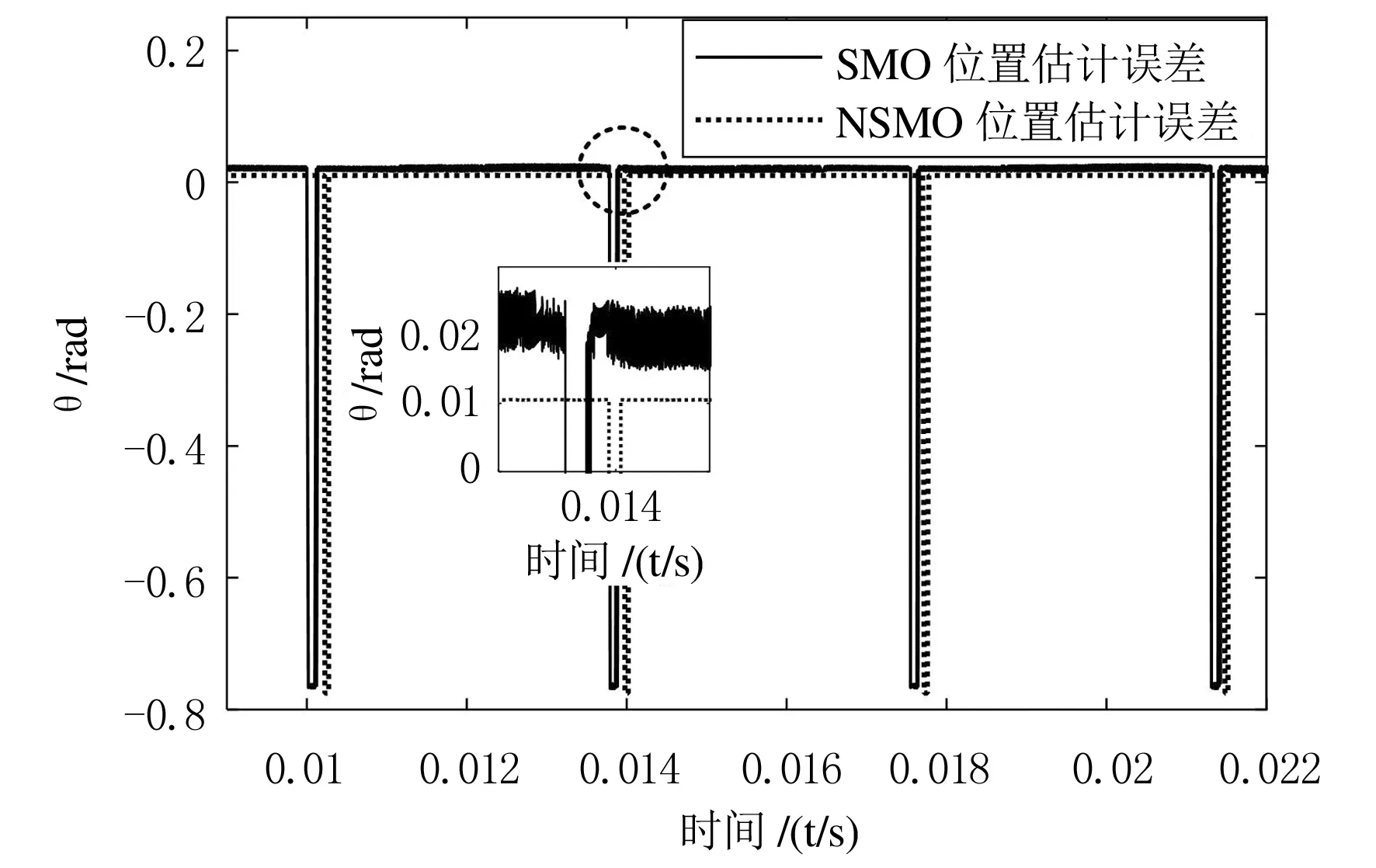
图7 传统SMO和NSMO转子位置估计误差
4 结语
本文以表贴式PMSM为研究对象,速度环采用ADRC控制器,使系统在初始启动和加速过程中都能快速稳定,当负载突变时,抗干扰能力较强.新型滑模观测器利用边界层可调的正弦输入函数,有效削弱了观测器抖振;通过反电动势观测器对反电动势进行提取,避免了低通滤波器的使用及由此带来的相位补偿问题,提高了系统的跟踪精度.

