一类非线性需求下渔业经济模型的动力学分析
周 欢
(兰州交通大学 数理学院,甘肃 兰州 730070)
资源的可持续利用是国内外学者研究的重要课题.当多个竞争个体共同利用公共资源时,谋利行为便是一个典型的博弈问题[1].对渔业经济的研究,通常用动态模型来描述资源数量的变化,进而获得最优的捕捞决策,制定一些措施来防止过度捕捞.Munro[2]与Levhari 等[3]是最早将渔业经济与博弈论结合起来的学者,其中Munro把渔业资源的动态模型与由 Nash 提出的两个个体合作理论结合在了一起; Levhari 和Mirman 主要研究了在离散区域内,两个体共同捕捞渔业资源的情形;Bischi[4]考虑了一个基于古诺寡头垄断博弈的多主体渔业经济模型,研究了非负平衡及其表示;顾恩国等[5]研究了具有不对称对手信息的两寡头博弈公共渔业资源的动力学模型.大多数模型中价格被看作是一个定值,但实际上价格取决于一些变量,如资源密度或捕捞努力量.Mansal[6]使用了关于价格的线性递减需求函数,获得稳定的无鱼平衡的情况,即渔业(捕捞努力量)在下降,而鱼类丰度趋于其承载能力.但是对于非线性需求函数,鱼类生物密度可以趋于零,而捕捞努力量仍然保持正的.Sidy Ly等[7]应用了一个价格的双曲线函数,考虑了资源的演变、不同地点之间的鱼类和船只流动、捕捞努力量和价格随供求关系而变化.事实上,在线性需求函数的情况下,存在一个最高价格,超过该价格,需求变为负(即等于零).相反,在双曲需求函数的情况下,即使价格非常高,需求仍然是正的.Brochier等[8]考虑可变价格的双曲需求函数,得出捕捞努力的流动性加上可变的鱼类价格导致了从当地过度开发到次区域可持续开发的转变.
在动态模型中研究非线性动力学行为是十分必要的.史晓琳[9]利用相图和时间序列图研究了几类关于捕捞函数的渔业经济模型.刘唯一[10]研究了几类生物模型中的不动点的稳定性与分岔.Li Hui等[11]研究了经济动力系统有两条不同的混沌路径,一条是通过flip分叉,另一条是通过Neimark-Sacker分叉.此外,吸引子和可行域也是许多学者感兴趣的问题.Bischi[12]研究了双寡头博弈中的多重稳定性和极限环.燕嘉敏[13]利用最大Lyapunov指数图,吸引子共存研究了异质企业的经济动力学模型.朱彦兰等[14]研究了系统中的吸引子的结构和数目随参数的变化.张亚鹏等[15]研究了吸引子共存时可行吸引域的演化.
因此,针对传统渔业经济模型中线性需求函数无法代表实际中较为多变情形的问题,本文考虑了突破市场最高价格后,仍存在需求的实际情形,建立了一个非线性需求函数下渔业资源存储量与捕捞量之间相互作用的多主体渔业经济模型,其中多个主体是完全不合作的且通过数值模拟与非线性动力学知识研究了参数如何变化时,渔业资源会得到可持续发展,并且个体获得更多的回报.
1 模型建立
假设有n个个体和m个市场,其中n,m>1.n个个体收获鱼,每个个体在m个市场上出售鱼.根据Brochie[8]采用的非线性需求函数,本文假定逆需求函数为
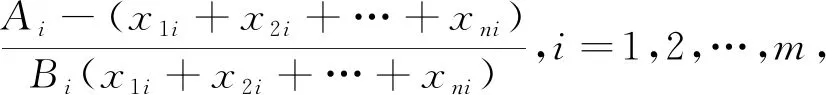
(1)
其中:Ai表示市场i(i=1,2,…,m)的价格等于0时的最大瞬时需求;Bi表示需求相对于价格的敏感度的参数;xki表示t时间内,个体k(k=1,2,…,n)收获并在市场i(i=1,2,…,m)上出售的鱼的数量.
令X(t)是在时间t时鱼类的总生物量,hk(t)是在时间t时个体k(k=1,2,…,n)收获(和出售)的鱼量,其中:hk(t)=xk1(t)+xk2(t)+…+xkm(t).
根据Clark[16]提出的柯布-道格拉斯函数,假设个体k(k=1,2,…,n)的捕捞成本函数为
(2)
其中:ck表示固定成本;γk表示技术参数.
假设si(t)=x1i(t)+x2i(t)+…+xni(t)为时间周期t内市场i(i=1,2,…,m)供应(和销售)的鱼量,且
H(t):=h1(t)+h2(t)+…+hn(t)=
s1(t)+s2(t)+…+sm(t).
(3)
假设每个个体都拥有完善的种群信息,在这种情况下,捕捞的鱼群的动态是由一维系统控制,
X(t+1)=
X(t)(1+α-βX(t))-H(t),
(4)
其中:α表示内在增长率;K=α/β表示环境承载力.
当多个主体在完全合作的情形下,每个个体k(k=1,2,…,n)通过最大化群体的整体利益来决定收获政策,则结合(1)和(2),可得个体k(k=1,2,…,n)在时期t的利润函数为
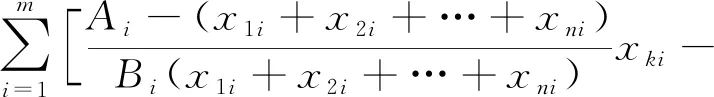
(5)
使得个体k(k=1,2,…,n)目标函数最大的一阶条件(边际利润)为
其中:π(t)是t时段多个主体的总利润,
假设每个个体决定其自身的收获活动,是使得参与的多个主体的联合利润最大化.每一时间段t所有个体决定t+1时段的捕捞量,必须形成其竞争对手的捕捞量的预期.则第k(k=1,2,…,n)个个体在t+1时段的捕捞量为
hk(t+1)=argmaxπk(hk(t),h-ke(t+1)),
(6)
其中:h-ke(t+1)表示第k(k=1,2,…,n)个个体关于其他个体的决策预期.

(7)

本文研究所有个体k(k=1,2,…,n)在市场i(i=1,2,…,m)出售的总捕捞量.因此对上式左右两边所有的i(i=1,2,…,m)和k(k=1,2,…,n)相加得到
(8)

(9)
(10)
结合(4)和(10),建立渔业资源储量与捕捞量之间相互作用的模型为

(11)

2 均衡点的存在性以及稳定性
系统(11)的不动点满足X(t+1)=X(t),H(t+1)=H(t),代入式(11),得
(12)
即不动点的坐标满足
X(t)(α-βX(t))=
(nbX(t))/(2mc).
(13)

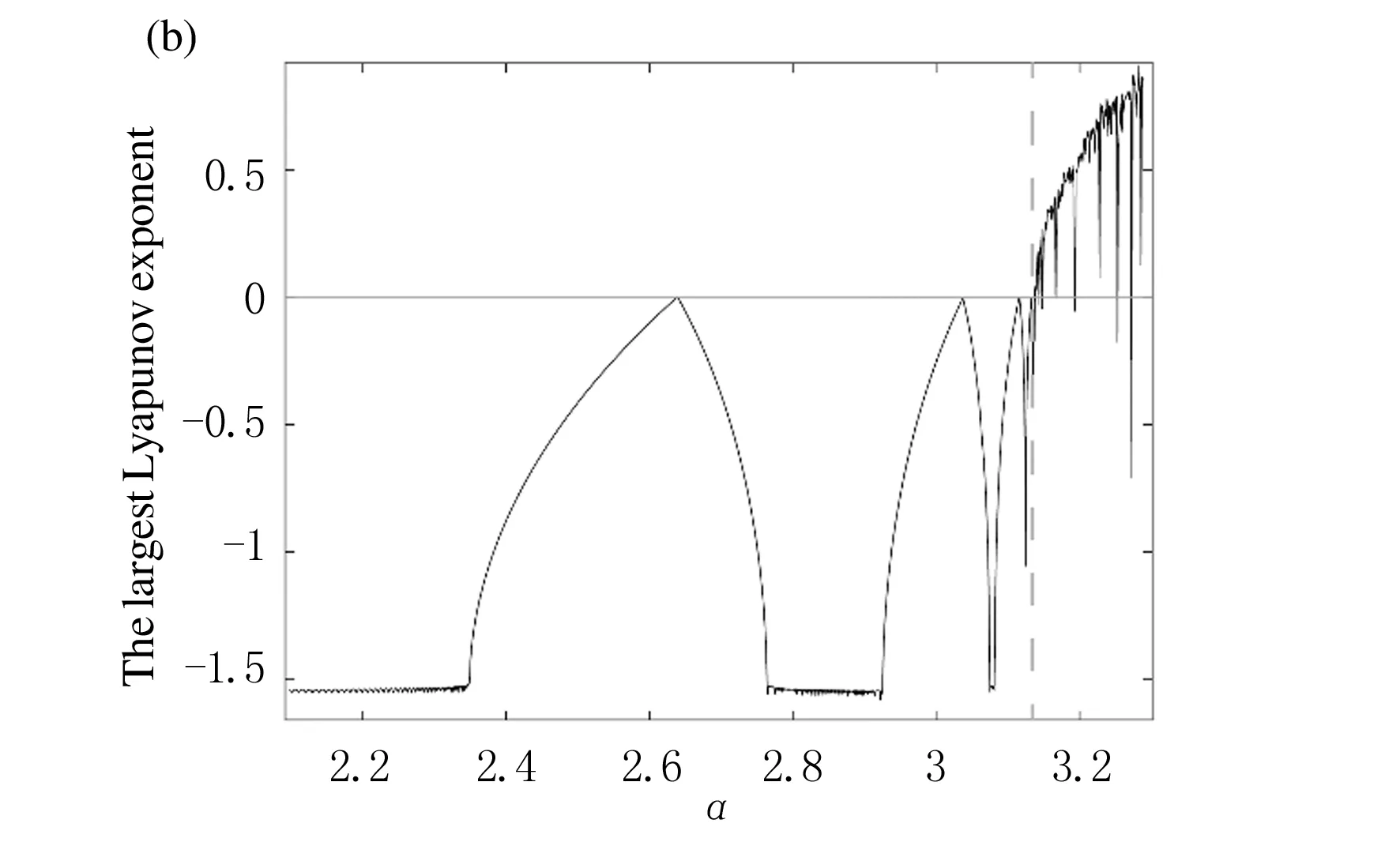
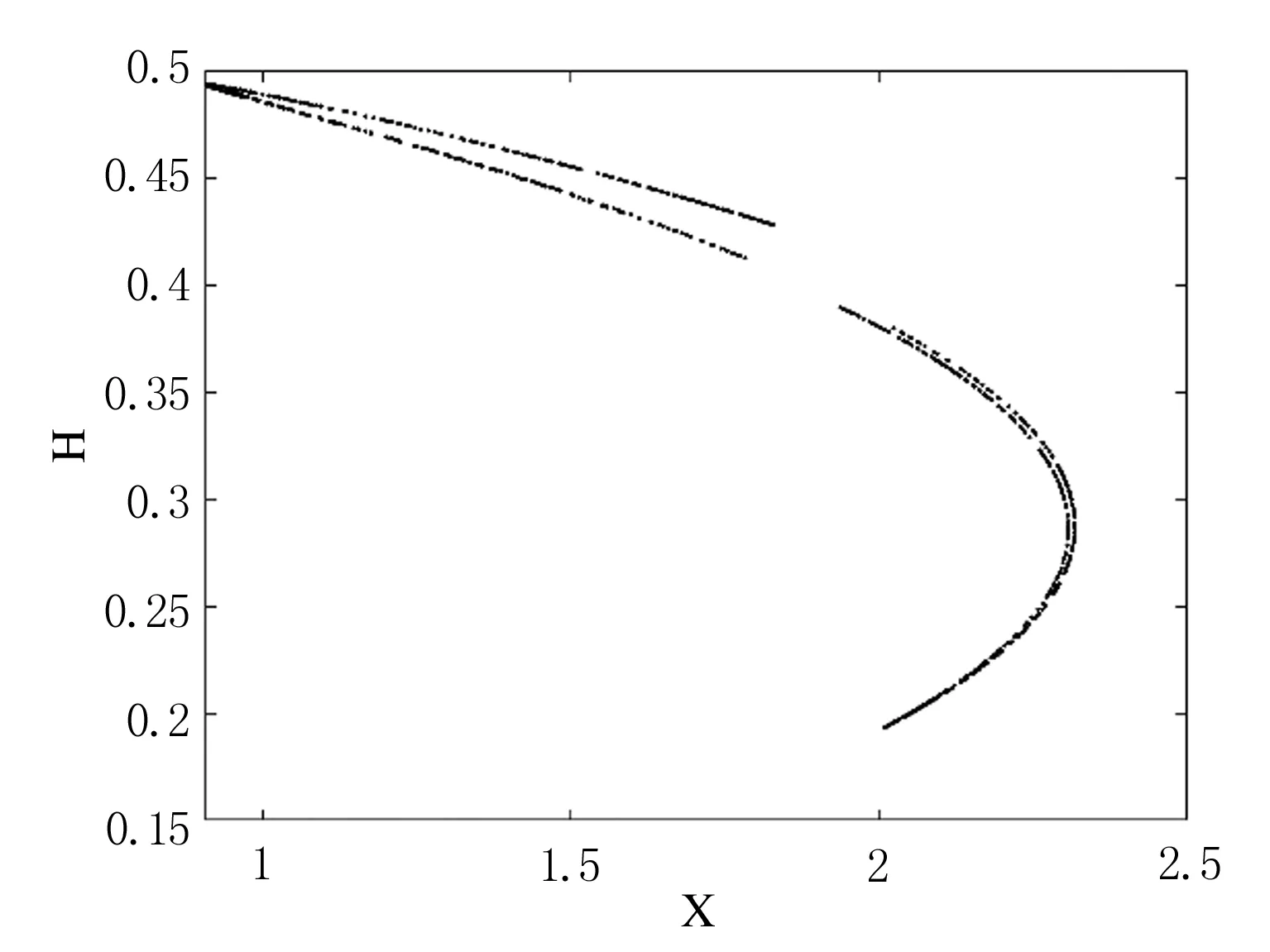
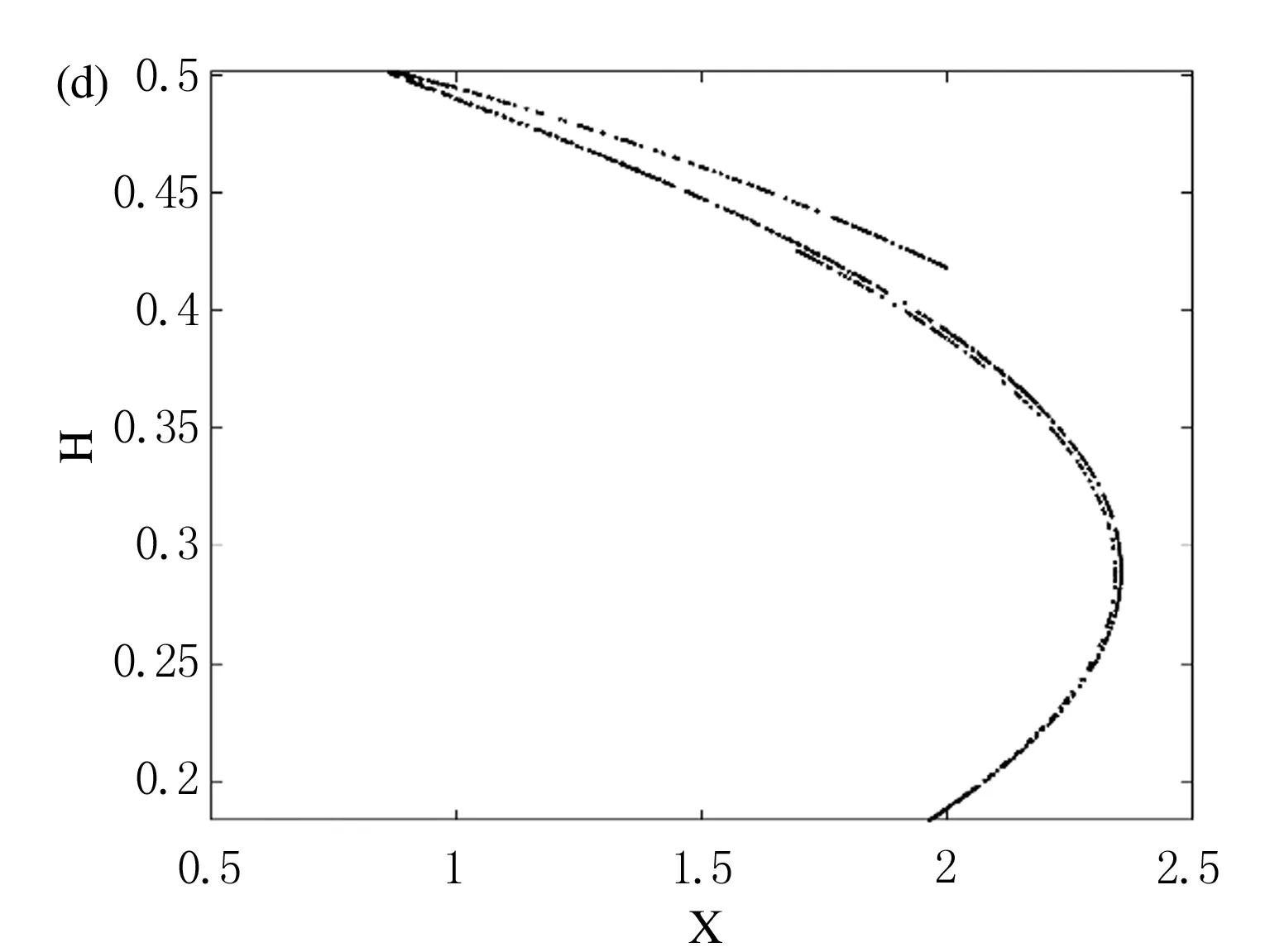
为了考虑模型本身的意义((X,H)∈{(X,H)|0 S={(b,c,α,β,n,m)|α>0,β>0, 系统(11)的Jacobi矩阵为 (14) 因此有以下命题. 命题1当满足下列条件时纳什均衡点E*是局部稳定的: (nb)/(2mc)<α<2+3M,M=min{1,α}. 证明系统在纳什均衡点E*处的Jacobi矩阵为 (15) J(E*)的特征多项式为 P(λ)=λ2-tr(J(E*))λ+det(J(E*))λ, 根据Jury判据: (i)1-trJ(E*)+detJ(E*)>0; (ii)1+trJ(E*)+detJ(E*)>0; (iii)1-detJ(E*)>0. 由条件S可知(i′)是恒成立的,根据条件(iii′)可得 结合条件(i′)和上式可得 (16) 化简条件(ii′),并将式(16)代入,则有 本节考虑有3个主体参与收获,并且在3个市场中出售所收获的鱼类,即n=m=3.当其他参数分别取α=2.5000,β=0.3570,b=1.3600,c=2.3400时,可得 计算该Jacobi矩阵的特征值,可得:λ1=-0.4594+0.2820i和λ2=-0.4594-0.2820i.根据二维离散动力系统均衡点的局部稳定性条件可知,Re(λ1)=Re(λ2)=-0.4594,均小于1,可以证实该纳什均衡点E*确实是一个稳定的焦点. 前面对纳什均衡点进行了稳定性分析,本节将通过数值模拟,利用单参数分岔图、吸引子和可行吸引域数目和结构的变化进行系统的动力学行为分析.在非线性动力系统中,系统参数的改变可能会导致系统动态行为的显著改变.此外,共存吸引子意味着系统的多稳态运动,即非线性系统的分岔演化行为随参数或初始条件的改变导致系统解数目的变化,分岔产生的稳定解导致了多个吸引子共存现象,因此多稳态运动被认为与分岔现象密切相关.在以下的数值模拟中,讨论两个主体参与收获并且在两个市场出售的情形,即:n=m=2;假定固定成本ck=0,并且假定两个参与者拥有同样技术捕获渔类生物,之后在相同的市场上出售. 首先根据文献[1],对系统(11)给出可行吸引域的定义. (17) 这里∂Ω表示可行吸引域Ω的边界.由(17)可知,X(t)的原象是H(t),因此可得 选取参数α=2.8075,β=0.5369,b=0.3500,c=2.9300,可以得到这组参数条件下的可行吸引域,如图1所示.此时,可行吸引域Ω是由H(t)在T-1的一次映射下得到的一阶原像H-1和X(t)轴所围成的区域,在图中用浅灰色标记. 图1 可行吸引域 由于纳什均衡点的稳定性与α,b,c有关,所以选取这3个参数作为分岔参数.首先固定参数β=1.5887,b=1.2100,c=2.8400,初始条件选取为(1.5000,0.9600),得到关于α的单参数分岔图,如图2(a)所示,黑色代表渔业资源存储量X(t),浅灰色代表总的捕获量H(t).可以发现系统在经历了一系列的flip分岔后,将从周期态进入混沌状态.其相应的一维最大Lyapunov指数图如图2(b)所示,分岔发生在最大Lyapunov指数等于零处,分别是2.6360,3.0380,3.1150,3.1330,3.1380等处.虽然在α∈(3.2220,3.2340)(图2(a)灰色虚线之间)时,单参数分岔图有一个小的“周期窗口”,此时系统处于短暂的6-周期,但是要想在实现多个主体利润最大化的同时,实现资源的可持续发展,需要将渔类生物的内在增长率控制在小于3.1380的范围内(图2(a)灰色虚线左侧),系统(11)才会处于一个稳定的状态. 为了研究“周期窗口”附近系统的状态变化,在图2相同的参数条件下,模拟参数α∈(3.1000,3.2300)系统中吸引子演化过程如图3所示.α=3.1000时,系统(11)存在着一个4-周期不动点吸引子,如图3(a)所示.随着内在增长率α的增加,这个不动点吸引子在α=3.1500通过局部分岔变为一个4-周期的混沌吸引子,如图3(b)所示.进一步增大α,4-周期的混沌吸引子的范围会不断变大,并且互相靠近,如图3(c)所示,在α=3.2000时,4-周期的吸引子变为2-周期的混沌吸引子.当内在增长率α持续增加至α=3.2300时,2-周期混沌吸引子进行了扩展合并的动态行为,最终形成一片混沌吸引子,如图3(d)所示. 图2 (a)关于α的单参数分岔图;(b)(a)对应的一维最大Lyapunov指数图 图3 吸引子的演化(a)α=3.1000;(b)α=3.1500;(c)α=3.2000;(d)α=3.2300. 最后研究参数c对系统稳定性的影响,固定参数α=2.9465,β=2.2380,b=1.1700.初始条件选取为(1.5300,0.3300)时,系统关于参数c的单参数分岔图如图5(a)所示,系统首先从1-周期态在c=1.3620时发生跳跃到7-周期态,之后在c=1.5420时又回到1-周期态,之后经历一系列flip分岔,最后进入混沌态.选取另外一组初始条件(0.9100,0.2200)时,系统的单参数分岔图如图5(b)所示.对比图5(a)和图5(b)可以看到系统在c∈(1.1800,1.5420)之间时(虚线之间),两幅单参数分岔图有明显的不同(灰色线处).图5(b)中系统从1-周期态跳跃到4-周期态,随后又进入1-周期态,之后又在c=1.4040发生跳跃到7-周期态,在c=1.5420时又回到1-周期,之后经历一系列flip分岔,最终进入混沌态.值得注意,在图5(b)中的跳跃发生了两次,分别是在c=1.1820和c=1.4040.以下利用可行吸引域和吸引子讨论单参数分岔图在这两处跳跃的原因.当c=1.1820时,系统(11)中存在两个吸引子,如图5(c)所示,一个是3-周期吸引子(用“*”标记),另外一个是1-周期吸引的不动点(用“☆”标记),这两个吸引子的吸引盆分别用黑色和灰色标记,逃逸区域用白色标记.这个1-周期的不动点是一个稳定的焦点,因为该点处的Jacobi矩阵为 计算可得特征值分别为λ1=-0.4783+0.5159i和λ2=-0.4783-0.5159i,Re(λ1)=Re(λ2)=-0.4783,均小于1.当c=1.4040时,系统中存在两个吸引子,如图5(d)所示,一个是6-周期吸引子(用“*”标记),另外一个是1-周期吸引的不动点(用“☆”标记),这个1-周期的不动点仍然是一个稳定的焦点,因为该点处的Jacobi矩阵为 计算可得特征值分别为λ1=-0.5566+0.3269i和λ2=-0.5566-0.3269i,Re(λ1)=Re(λ2)=-0.5566,均小于1.综上所述,单参数分岔图中出现跳跃现象的原因是吸引子共存. 除此之外,从两组单参数分岔图发现,系统每隔一段时间就会发生同样的分岔行为,这在可行域内就是可行吸引域的自相似结构.图5(c)和图5(d)的可行吸引域的形状像一座桥.不同吸引子的吸引盆的形状像桥洞,每座大桥里面又有很多小桥和小桥洞.图5中的自相似结构是一种弱分形结构[1],因为可行吸引域边界上只有有限个尖点.综合以上所述,当成本参数c保持在(1.5000,4.2000)之间时,系统将会保持在一个稳定的状态,在这个范围内渔类的生物量和各个主体捕捞量会实现可持续发展,而且多个主体也会获得更多的收益. 针对传统渔业经济模型中线性需求函数无法代表实际中较为多变情形的问题,本文考虑了突破市场最高价格后,仍存在需求的实际情形,建立了一个非线性需求函数下渔业资源存储量与捕捞量之间相互作用的多主体渔业经济模型.其中多主体之间是完全合作,他们以集体利益最大化作为自己下一阶段的收获决策.利用系统的Jacobi矩阵和Jury判据讨论了不动点及其局部稳定性.随后讨论了各个参数条件对系统稳定性的影响,根据单参数分岔图,价格敏感性和生物的内在增长率相对较小,成本参数保持在一定范围内时,将有助于渔业资源的可持续发展,参与的多个主体也会获得更多的回报.然后通过奇异吸引子的演化分析发现系统具有良好的自相似结构;通过系统的多稳态性分析发现由于吸引子的共存会让单参数分岔图有跳跃现象;通过吸引子与其吸引盆的接触导致的“边界危机”, 研究可行吸引域结构的变化.此外,通过可行吸引域的形状和大小,可以防止过度捕捞、鱼类资源枯竭和经济效益低下.对这一复杂系统的分析会支持渔业资源的可持续发展,也会增加各个主体的经济收益. 图4 (a)关于b的单参数分岔图;(b)b=0.3518时系统(11)的可行吸引域; 图5 (a)初始条件选取为(1.5300,0.3300)分岔参数c的单参数分岔图;(b)初始条件选取为
α>(nb)/(2mc),c≠0,n>1,m>1}.


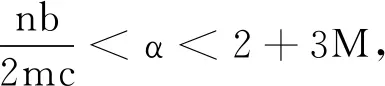

3 数值模拟
3.1 可行吸引域




3.2 参数对系统稳定性的影响




4 结语









