基于NMI-FA-DELM 模型的土壤热导率预测

雷宇 黄亦凡 罗学东 周盛涛 付超

（中国地质大学（武汉）工程学院，湖北 武汉 430074）

土壤热导率控制着稳定状态下土壤内的热传导过程，是土壤物理学水、热、溶质耦合数值模型的重要参数之一，也是研究土壤水分蒸发模拟、气象和地球物理过程的基础［1-6］；同时，土壤热导率是影响地下温度分布的重要土壤参数，在岩土工程和土木工程施工设计中有重要意义。目前，热脉冲法是测量土壤热导率较为有效的方法，但土壤是多相介质，其热特性受到固体、气体和液体等的影响［7-8］，大规模准确测量土壤热导率较为困难。因此，快速、简单、精准预测土壤热导率是很有必要的。

在土壤热导率预测领域，国内外学者提出了大量预测方程来描述土壤热导率与土壤饱和程度、容重、孔隙率、土壤颗粒形状和石英含量等影响参数之间的关系［9］。其中，预测方程分为理论模型和经验模型。理论模型是通过理论基础进行预测，Wiener［10］基于串联模型和并联模型经典混合定律对热导率进行预测，但其没有针对土壤热导率设置参数，不适用于土壤。Vries［11］假设土壤固体颗粒在连续孔隙流中均匀分布，提出了预测精度较高的预测模型，但公式十分复杂，所需参数难以确定。经验模型是通过拟合实验测量结果提出公式，Kersten［12］将土壤含水量和干容重作为参数，通过曲线拟合建立模型，其预测精度不足，忽略了土壤其他有关因素。Chen［13］根据经验拟合多组石英砂岩实验数据，建立拟合模型，但其模型只对砂岩适用，对其他类型土壤的预测结果精度较低。

近年来，使用机器学习方法来预测土壤热导率得到了大量的关注。机器学习通过分析大量数据块进行自我学习，并应用于回归、聚类和分类，能有效解决复杂的高度非线性预测问题。Rizvi等［14］使用深度神经网络（DNN）来预测不同孔隙度和水分含量值沙子的有效热导率，发现预测结果在合理误差范围内。Zhang 等［15］建立了一个用于预测非饱和土壤热导率的ANN模型，该模型可以定量、系统考虑多种影响因素对土壤热导率的耦合效应。Jiang等［16］建立了一个含有101组数据的数据集，通过极限学习机（DELM）模型预测了岩石热导率，同时通过与支持向量回归（SVR）和反向传播神经网络（BPNN）的对比，证明了DELM 在预测热导率方面有良好的性能。极限学习机中，输入量的选择和节点的参数选取能影响预测结果，因此，有必要对极限学习机进行优化，以提高预测模型的预测效果。

本文选取257组数据作为训练集，全面选取影响土壤热导率的6个因素作为输入量，构建基于归一化互信息法（NMI）下的萤火虫算法（FA）优化极限学习机（DELM）预测模型，用于预测土壤热导率，并对比分析统计方程、DELM、随机森林、BP神经网络和SVR预测模型的预测效果，同时用均方根误差、平均绝对百分比误差、a10指数和决定系数4种评价指标来综合评价模型预测效果。此外，通过模型对输入量的筛选，研究了各输入量对预测结果的重要性。

用语言去学专业知识的同时也在学习使用这种语言。教师应该鼓励学生在教室参加有意义的互动互动。增加学生发言时间，减少教师发言时间。这种交流也包括适当的母语及语码转换等，这些主要是帮助教学活动顺利进行，如教师用母语发出指令等。经过一段时间的适应后，无论教师还是学生都要尽力减少使用母语和语码转换。学生如果能较多地使用目标语讨论学科知识内容，则教学目标相对较好地实现了。

1 NMI、FA、DELM算法介绍

1.1 归一化互信息法

归一化互信息作为评价两个变量之间相关性的参数，不仅代表两个变量共同拥有的内容信息，而且能反映当一个变量变化时，另一个变量随之变化的程度［17］。在机器学习中，归一化互信息常用来反映输入量对输出量的敏感性。如果输入量与输出量之间完全不相关或相互独立，那么它们的相互信息为0，这意味着它们之间不存在相同的信息，则可认为输入量对输出结果没有贡献。一般来说，相互信息的值越高，输入量与输出量中包含的相同信息就越多，则表示输入量对输出量的贡献值越大，输入量的选择越可靠。

假设随机变量A=｛a1，a2，…，an｝、B=｛b1，b2，…，bn｝，则变量A和变量B的互信息可以通过以下方式获得：

式中，H（A，B）为这两个随机变量的联合分布，H（A）和H（B）分别为变量A和变量B的信息熵，相互信息I（A/B）为联合分布H（A，B）和积分布H（A）H（B）的相对熵。为了比较所有输入变量的重要性，相互信息应按以下公式进行归一化：

式中，F（A/B）为归一化互信息。变量A和变量B之间的相关程度如图1所示。

分析数据集输入值与输出值的皮尔逊相关系数r，得到数据矩阵图，如图6所示。由图可知，它们之间的相关系数绝大部分小于0.60，说明选择的输入量与输出结果之间的相关性较小，存在复杂的非线性关系。

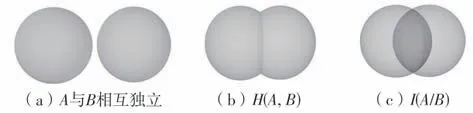
图1 归一化互信息法示意图Fig.1 Schematic diagram of normalized mutual information

1.2 萤火虫优化算法

式中，w为土壤含水率，γd为土壤的干容重。

图2 萤火虫算法示意图Fig.2 Schematic diagram of firefly algorithm

在萤火虫优化算法中，遵循如下3 条规则：①算法中不考虑萤火虫个体的性别差异因素，即所有萤火虫个体都视作是同性的。②萤火虫的吸引力与它们的发光亮度相关，对于任意两个萤火虫个体，发光亮度较强的将吸引发光亮度较弱的萤火虫，同时吸引力也会随着萤火虫之间距离的增加而减小。对于特定发光最亮的萤火虫个体，将在搜索空间随机移动。③在实际应用中，萤火虫个体的发光亮度一般是与求解目标函数值相关联的，通常，目标函数值就视为萤火虫在该处的发光亮度［19］。

萤火虫优化算法寻优过程中最重要的因素是萤火虫的自身亮度和吸引度。亮度在实际操作中一般视作为其当前所处位置的目标函数值，亮度函数M（d）可表示为

采用ABAQUS对5个模型进行模拟，模型中梁、柱采用B31纤维梁单元，由于纤维梁单元截面属性单一，框架梁、柱中的竖向钢筋需要通过编写ABAQUS软件形成的INP文件添加.框架柱中的箍筋通过添加TRANSVERSE SHEAR STIFFNESS参数来定义.运算时调用PQ-Fiber子程序，赋予材料属性.混凝土选用混凝土单轴弹塑性滞回本构模型，钢筋选用钢材的单轴弹塑性滞回本构模型(USteel02).图5为混凝土和钢筋的本构关系.

式中：M0为萤火虫初始亮度，即为萤火虫最大亮度；d为两萤火虫个体之间的距离；γ为光强吸收系数，用于表征光在介质中传播的损耗。萤火虫亮度越高代表其所处的位置越好，即目标函数值越优。相应地，在算法中亮度更高的萤火虫个体会具有更强的吸引力，这样就会把周围视野区域内亮度相对较弱的同伴吸引过来，吸引力函数β（d）可表示为

式中，β0为光源处即d为零时的吸引力。

萤火虫种群中，若两萤火虫个体i与j分别位于Xi和Xj位置，它们之间的距离可用欧式距离dij表示为

河流水质表达的本质是关于“污染物量”与“水量”的二元函数，河流天然“水量”的年际变化影响，远远大于人类的排放活动对河流水质的影响，需要约束的是“污染物量”的排放。

那人在离他不远的地方蹲下了，开始撒尿。一缕月光斜斜地照亮了这个人的半边脸，嘴角上有颗大大的黑痣。啊——甲洛洛几乎叫出了声，原来，原来这个嘎绒是偷人。

我们根据数据与处理一节表述的数据，采用第一个被触发台站周围的平坦先验和每个质点滤波定义1 000个质点，进行了质点滤波参数估计近似。这个方法以1s的时间间隔进行更新，而且所有的实验都在模拟的实时中进行。

式中，D为目标问题的空间维度，Xik为第i个萤火虫在k维上的坐标。

发光亮度较弱的萤火虫i将移向发光亮度较强的萤火虫j，其位置逐步更新，更新公式为

式中，t为算法当前迭代次数，α为步长因子，rand为［0，1］上均匀分布的随机实数。

萤火虫种群中，亮度最高的萤火虫位置更新方程为

式中，Xbest，i为亮度最高的萤火虫位置。

研究的结果表明学生总体来说缺乏与策略相关的意识。他们相对来说缺乏丰富的策略储备，例如他们对学习策略不大了解。因此，他们不能实施恰当的学习策略和有意识的控制学习策略的使用[6]。所有这些都说明学生在不同的语言学习任务中实施恰当的学习策略以及控制策略使用方面的能力比较低。因此学习策略的培训也是迫在眉睫。学习策略的训练旨在帮助学习者考量影响自己学习的因素，找到最适合自己的学习策略，这样学习者才可能更有效的学习，并且对自己的学习负责。它更加关注的是学习过程，因此强调是如何学而不是学什么。因此高校应尽可能地为非英语专业大学生自主学习英语的过程中提供相应的帮助和指导，让学生掌握如何自主学习英语的能力。

1.3 深度极限学习机

DELM 是一种以自动编码器极限学习机（ELMAE）作为基础单元的深度学习算法，一般由输入层、隐藏层和输出层组成。极限学习机（ELM）是一种有监督的学习方法，其网络训练的输入权重和偏置是随机产生的，不需要人工设置大量的网络参数，这使其有较快的学习速度。而自动编码器AE的训练是不受监督的，经过训练可以将输入复制到输出［20-22］。自动编码器极限学习机可以很好地实现维度的压缩，并高质量地维持原始数据的特征表达。将DELM 的每个隐藏层都用ELM-AE初始化，执行分层无监督训练，可以最大限度地降低重构误差，从而达到精准预测的目的，其模型训练过程如图3所示。

图3 DELM模型示意图Fig.3 Schematic diagram of DELM model

2 NMI-FA-DELM模型的构建

①落实管护人员，明确管护责任。北京市政府印发了《关于建立本市农村水务建设与管理机制意见的通知》。全市成立3927个农民用水协会，政府通过购买服务的方式 （每人每月500元补助）组建了10800名农民管水员队伍，负责农村水土保持、机井管理、用水计量、水资源费征收、河道管护等工作，实现了源头管理。北京市政府建立了水源涵养林管护机制，出台了山区移民搬迁政策 （每人每月400元补助）组建了4万多名生态林管护员队伍，使全市61万hm2水源涵养林实现了管护全覆盖。

基于NMI-FA-DELM模型的土壤热导率预测模型如图4所示，主要可以分为数据集处理模块、FA模块和DELM 模块，其中，DELM 模块根据FA传入的参数进行分析，获得隐藏层的节点数，以此来构建DELM预测网络模型。数据集经过NMI处理后分为训练集和测试集。为了避免数据范围和量级对模型的精度造成影响，将数据进行归一化处理，公式如下：

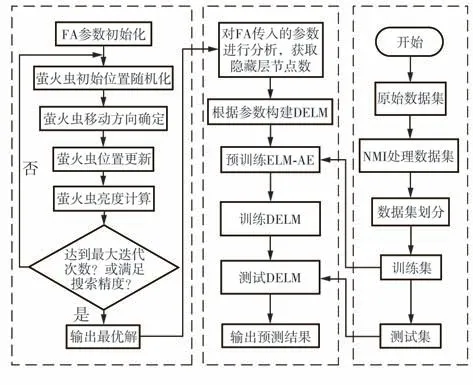
图4 NMI-FA-DELM模型流程图Fig.4 NMI-FA-DELM model flow chart

式中，xnorm为数据的归一化值，x为某一指标数据，min（x）为某一指标中的最小数据，max（x）为某一指标中的最大数据。

然后将数据参数进行归一化处理，通过DELM模型由训练集数据训练ELM-AE，接着训练DELM。模型将训练集的均方根误差（ERMSE）作为适应度函数，其计算公式如下：

式中，N为样本总数，为预测值，yi为实测值。

之后，模型将适应度值返回给FA。FA 根据适应度值更新萤火虫的移动位置，实现全局最优解的更新，直到满足循环条件后，输出最终预测结果。同时，该模型可以很好地通过Matlab 等软件实现，并很好地适用于生产实际之中。

3 土壤热导率预测算例分析

3.1 数据集的选取

本次数据库共选取257 组土壤热导率测量值，如表1 所示。数据库中第1 至160 组数据来自于Tarnawski 等［23］对加拿大9 个省份的40 块田间的土壤样品测试；第161 至240 组数据来自于Chen［24］和Zhang 等［25］对几种不同级配石英砂进行的测试；第241、242 组数据来自于Mccombie 等［26］对意大利罗马附近的粗火山碎屑土进行的测试；第243 至257组数据来自于Tarnawski等［27］对日本北海道附件的火山灰土壤和加拿大渥太华的土壤进行的测试。数据集中每组数据包括7个参数，分别为土壤干密度（ρd）、孔隙度（n）、饱和程度（Sr）、石英含量（mq）、含沙量（ms）、粘性土含量（mc）和土壤热导率（K），其中含量以质量分数计。将ρd、n、Sr、mq、ms、mc作为预测输入量，这些输入量在理论分析中对土壤热导率的影响较大，且其测试较为经济和方便，在大量已经存在的预测模型中表现良好［9，28-29］；土壤热导率作为预测结果。数据集数据中无离群数据，数据库结构合理，其分布情况如图5所示。

表1 数据集［23-27］Table 1 Data set［23-27］

图5 数据集小提琴图Fig.5 Data set violin diagram

并不是所有撒料区域都符合需要撒料的条件.例如，若某些区域面积过小，可能会导致装甑撒料执行机构最小撒料量大于实际所需撒料量，故可以根据分割完成的撒料区域所拥有的像素点数量对撒料区域做进一步的筛选，并将撒料区域像素点的数量作为撒料区域面积.图7是撒料区域面积大于的撒料区域，并保留图6中的编号.

图6 数据集矩阵图Fig.6 Data set matrix

本文将数据库数据的80%作为训练集，20%作为测试集，即207组数据作为训练集和50组数据作为测试集［31］。为获得模型的最佳参数，开发了8个不同参数值的NMI-FA-DELM 模型。多个模型中，设置模型萤火虫种群数量从20到200不等，最大吸引度值β0为2，光强吸收系数γ为1，初始化步长因子为0.2。通过均方根误差判定上述模型效果，如图9 所示。结果显示，当迭代次数达到500 后，均方根误差几乎不再变化，当种群数量为60 时，模型达到最佳效果，其均方根误差为0.363。

图7 热脉冲法测量装置图Fig.7 Heat pulse method measurement device diagram

3.2 输入量的选取

将NMI-FA-DELM 模型与统计预测方程、极限学习机、随机森林、BP神经网络和SVR这5种常见预测模型进行比较，其中统计预测方程是利用Kersten［12］所提出的经验公式进行拟合，其经验公式如下：

图8 输入量归一化互信息值图Fig.8 Input normalized mutual information value diagram

3.3 模型参数的设置

采用热脉冲法（也称瞬态法）来测量土壤热导率［30］。此方法可以在测量过程中有效地避免水分的迁移，其测量装置如图7所示。

3.4 NMI-FA-DELM预测结果

根据上述研究参数对NMI-FA-DELM 预测模型进行修正。为考察修正模型预测结果，利用均方根误差（ERMSE）［32］、平均绝对百分比误差（EMAPE）［33］、a10指数（a10）［34］和决定系数（R2）4种评价指标来综合评价模型预测效果。

式中，为实测值均值，m10 为测试集中测试值与实测值的比值在0.9到1.1之间的样本数。

本文NMI-FA-DELM 模型中的6 个输入量在一定程度上都影响着土壤热导率的预测结果，但各输入量显著性水平尚未明晰，需要进一步验证。本模型采用归一化互信息法NMI，通过计算6 个输入量对输出量的敏感性，对各输入量进行分析，以此评估各个输入对模型的重要性，其计算结果如图8所示。由图可以看出6个输入量的归一化互信息值都大于0.5，说明6 个参数都可以作为本模型的输入量，且对土壤热导率影响最大的是粘性土含量，最小的是石英含量。

萤火虫优化算法是一种新型的基于种群搜索的优化算法，该算法概念简单、流程清晰、参数设置较少、没有变异和交叉等复杂操作，易于实现和操作［18］。萤火虫优化算法的灵感来源于萤火虫在求偶、捕食、警戒等过程中的发光行为。萤火虫通过搜索周围发光更亮的同伴，逐渐朝着区域内较亮的位置移动，从而最终聚集到最亮即最优的位置，实现搜索最优解的功能，如图2所示。

6 种模型的预测结果如图10 所示，可以看出NMI-FA-DELM 的误差相对最小，其R2达到了0.961，平均绝对百分比误差（9.667%）在10%之内，而统计预测方程的误差值最大，R2仅为0.375，平均绝对百分比误差达到44.48%，同时没有优化的DELM 模型比NMI-FA-DELM 模型的效果差，其R2为0.807，平均绝对百分比误差为22.714%。

图10 不同方法土壤热导率的预测值与实测值的对比Fig.10 Comparison of prediction results of different methods and actual measurement results

为综合评价这6种模型，本文通过综合评价方法对模型进行打分；为了防止两个相近数据被分为不同等级而导致分数差距较大，本文对模型指标的数值进行归一化处理，并作为模型指标的得分，同时对得分进行累加［35］。训练集与测试集的分析结果如