基于统一标签矩阵的快速多视图聚类

刘怡俊 王嘉达 钟仕杰 杨晓君† 叶武剑

（1.广东工业大学 集成电路学院，广东 广州 510006；2.广东工业大学 先进制造学院，广东 揭阳 515200；3.广东工业大学 信息工程学院，广东 广州 510006）

数据集可以通过多个视图、不同的来源和异构属性进行编码［1-2］。基于这类数据集产生了一种聚类方法，称为多视图聚类［3-4］。这种方法可以学习来自不同观点的互补信息，并输出一致的结果。例如，在自然语言处理中，文档通常可以用多种语言表示。每种语言都表示一个视图，Kumar 等［5］提出的共正则化谱聚类（CoregSC）在这个领域中已经成为常用的数据处理方法。

众多学者对多视图学习进行了充分的研究分析与讨论［6-7］。目前，多视图聚类方法包括协作训练方法［8-9］、多核学习方法［10］和基于图的方法［11-12］等类型。由于基于图的聚类方法通过考虑不同视图之间的多样性信息和互补信息，可以有效地挖掘出数据的潜在信息，所以性能更为出色［13］。本文主要研究基于图的多视图聚类。

近年来，有众多学者提出在单视图聚类的基础上拓展多视图聚类的方法。Zhou 等［14］通过将归一化切割从单视图扩展到多视图，提出了一种多视图聚类方法；Cai 等［15］为每个特征描述建立了一个模型，然后将这些模型统一起来学习一个拉普拉斯矩阵；Liu 等［16］通过联合非负矩阵分解的方法（Multi-NMF）提出了多视图聚类，采用了一种共正则化策略来融合视图间的信息；为了处理大规模数据集，Li等［17］使用二部图构造相似性矩阵，发现了对每个视图独立使用流形融合或k-means 的不可行性；Zhan 等［18］提出了一种新的目标函数，通过最小化不同视图之间的差异来学习统一图，并在拉普拉斯矩阵中添加了秩约束，提出多视图一致图的聚类（MCGL）；为了直接获得聚类结果，Cai等［19］提出了一种新的鲁棒多视图k-means 聚类方法（MkC），该方法可以通过分解每个视图数据特征直接获得聚类结果；Xia 等［20］提出的基于低秩和稀疏分解的鲁棒多视图谱聚类（MSC），首先为每个视图构造了一个概率转移矩阵，然后恢复低秩概率转移矩阵，最后将公共矩阵输入到马尔可夫链方法中，得到聚类结果；Zhu 等［21］提出了一种一步多视图谱聚类，该方法从低维数据中学习亲和矩阵。

上述方法可以根据是否生成一致图分为两类。对于需要生成一致图的方法，其无法避免对一致图矩阵采用其他聚类方法进行处理，容易导致聚类结果产生次优解；对于不需要生成一致图的方法，通常具有更为出色的性能，但由于需要进行特征分解，所以时间复杂度很高且需要后处理。

针对产生次优解、高时间复杂度以及需要后处理等缺陷，本研究基于图重建、聚类结果的可解释性和时间成本，提出了一种新颖的多视图聚类模型。该模型不需要构建统一图，同时也避免了特征分解以降低时间复杂度并避免后处理，从而提升运行速度。该方法首先从传统的谱聚类（SC）中归一化切割（SNcut）和比例切割（SRcut）的统一观点出发，将非负约束和正交约束作为结构化约束构建模型；其次，随机选取锚点的地址，将每个视图中对应地址的数据定义为锚点，并嵌入到相似矩阵中，可以免去前处理（例如k-means）的迭代计算；同时，将多个视图的数据对齐；最后，通过非负的统一标签矩阵快速迭代更新。

1 相关工作

1.1 单视图谱聚类

谱聚类是一种近似于SRcut（或SNcut）的聚类方法［22］。而对子图的最小化切割极有可能是简单的将某个顶点从其他顶点的集合中切割下来。为了保证切割后每个子图的大小平衡，需要借助SRcut 和SNcut。其目标函数如下：

其中，非空子集需要满足Ai∩Aj=∅(i，j=1，2，…，c)和Ai∪，…，∪Ac={v1，v2，…，vn}。但是，为使子图大小均匀，以上两个需要解决的问题均为NP 难，因此，需要松弛上述两个问题。设指示矩阵为F∈Rn×c，则第j列向量用fj来表示。在SNcut 中，第i行的fj表示为

由式（3）可得，=cut(Aj)/vol(Aj)和FTDF=Ic，其中Ic为c阶单位矩阵。由此可将式（2）的SNcut问题转化为迹的形式：

其中，F需要满足式（3）。该问题对SNcut进行松弛后，则可以忽略离散化的要求，同时保留正交约束。若设H=D1/2F，代入到式（4）则可以将问题转化为

式（5）即为松弛的归一化谱聚类的目标函数。类似地，将式（3）中定义指示矩阵时的vo（lAi）j改为 |Aj|，可得松弛的SRcut的目标函数：

可以对L或进行特征分解，再从前c个最小特征值对应的特征向量来获得F或H的最优解，并对其行向量进行k-means来获得聚类标签。

1.2 多视图谱聚类

在现实世界中，由于单视图数据无法对事物完整地进行描述，因此，数据通常用多个异构源来描述，从而形成多视图数据［23］。由1.1节可以写出对应的多视图谱聚类目标函数：

式中，L（v）为第v个视图的图拉普拉斯矩阵。显然，这个目标函数存在问题，无法满足多视图聚类的需要。主要问题有3个：其一，式（7）没有考虑不同视图之间的关系，在多次迭代后，指示矩阵F无法得到一致性嵌入，从而无法准确地形成多视图指示矩阵；其二，依然没有摆脱后处理的限制，由于k-means算法对初始化敏感，不同的初始点将导致聚类结果不同，因此，后处理使得聚类结果不鲁棒；其三，该方法需要特征分解，这将导致计算复杂度和时间成本的大幅提升。有众多研究者对这一公式通过添加非归一化系数、增加正则项等手段进行优化，如文献［4］和［24］。本研究将通过增加平衡项和平衡系数来实现聚类算法的快速收敛并摆脱后处理的限制。

1.3 随机选取锚点地址

在单视图聚类中，选取的锚点通常是作为聚类中心，以提升聚类的速度和性能。但是，在多视图聚类中，需要无监督地学习不同视图之间的联系和差异。

目前，主流的锚点选择方式有k-means 和随机选取等［17］。其中，k-means 选取的锚点无法保证每个视图能够对齐，因此，本研究采用随机选取锚点地址的方法。如图1所示，以3行6列的矩阵为例，在一个矩阵中的5 个虚线矩形表示锚点所在位置。随机选取锚点地址的方法通常是随机选取同一个视图中的m个锚点地址，然后将其应用到每一个视图中。该方法选取的锚点不需要表示原始数据的特征，其主要目的是对齐各个视图。

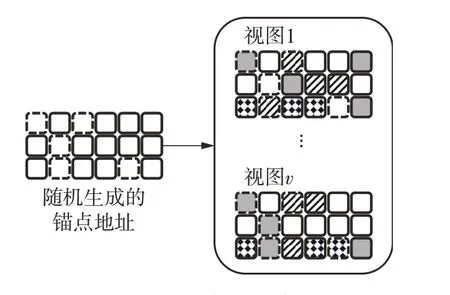
图1 锚点嵌入示意图Fig.1 Schematic diagram of anchor embedding

该方法主要有3个优势：其一，由于其随机性可以避免偏见选择，所以可提升准确性；其二，计算复杂度较低，可以保证在提升准确性的同时将时间成本降低；其三，具有广泛的适用性，能够适用于不同的数据类型，例如数值型数据、类别型数据和文本数据等。

2 基于统一标签矩阵的快速多视图聚类

本研究提出了一种无监督学习方法，即基于统一标签矩阵的快速多视图聚类（FMCULM），如图2所示。通过将多视图数据矩阵转化为嵌入锚点的相似图后，对标签矩阵进行迭代更新，从而使模型在最少的迭代次数后达到收敛；最后通过标签矩阵直接得出聚类结果。

图2 FMCULM方法框架Fig.2 Framework of FMCULM

2.1 算法思想

在谱聚类中，特征分解得到的拉普拉斯矩阵的特征向量就是指示向量。这一方法使得聚类失去了可解释性，故而十分依赖于后处理，可以把后处理理解为是对连续值重新离散化的过程［18］。如果想摆脱后处理，就需要在切图时避免过分的松弛［25］。因此，需要对式（7）增加非负约束，从而得到

本文从4个方面解释式（8）提出的模型。其一，该模型与谱聚类相比更接近SRcut（SNcut），因为在式（8）的模型和SRcut（SNcut）中的指标矩阵均有非负元素，而谱聚类将其松弛为实数。其二，在同一个簇中的两个样本可能具有不同的相似性，而SRcut（SNcut）在同一个簇内应该具有相同的相似性。其三，非负约束使式（8）提供了聚类的可解释性，即F的元素能反映数据和簇之间联系的紧密程度。其四，该问题是一个具有正交非负约束的问题，实质上式（8）的解已经具备离散性。如图3 所示，假设F∈R3×9，表示有9 个数据点分别隶属于3 个不同的簇。白色方块表示值为零的元素，其他方块表示非零元素。由于约束，使得F的每一行有且仅有一个非零元素，且每一列的L2范数为1。F为离散稀疏又具有物理意义的矩阵，其物理意义是F中元素的数值可以直接表示数据点和簇之间的关系。

图3 正交约束示意图Fig.3 Schematic diagram of orthogonal constraints

若相似矩阵W是一个双随机矩阵，即W的每一行和每一列所有元素之和为1的矩阵，则度矩阵是一个单位矩阵。那么L-I-W=，且F=H。此时，图拉普拉斯矩阵已经标准化，则式（5）与（6）完全等价。这就是从SNcut 和SRcut 的统一观点出发得出的结论。在后续分析中，默认W是双随机矩阵，同时也是结构化图。因此，可以通过命题1进一步变换等式（8）为式（9）。

命题1求解式（8）等价于求解

证明设W为对称的双随机矩阵，常数项为

在本研究中，式（9）是一种十分重要的模型，可以理解为是一种基于正交非负约束的图重构。因为原始图的构建通常在数据中存在噪声，所以没有清晰的结构，因此在学习结构化图时，图重构是一种优化过程。如图4 所示，M中每一个块对应一个连通分量，而一个连通分量属于同一个簇。在大多数情况下，一个连通分量直接对应一个簇。式（9）的目标是通过对角分块矩阵重构相似矩阵，重构后的矩阵需要与原始图W相似，即用具有结构信息的重构图来近似原始图。这种清晰的结构包含了很多关于簇类的准确信息。在图4 中，矩阵M的3 个位于对角线上的块矩阵之间具有显著差异。然而，在块内的数据不完全相同，但具有相似之处，因此这是一个十分优秀的模型，在聚类过程中可以保证既关注聚类标签又关注簇内的差异。

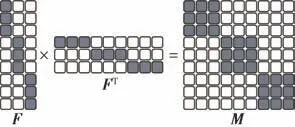
图4 图重构示意图Fig.4 Schematic diagram of reconstructed graph

因此，本研究的目标函数为

式中：第1 项是重构项，用于硬聚类；第2 项为平衡项，用于软聚类；λ为平衡系数，用于保持两项之间的平衡。当λ足够大时，F与G将无限接近，式（10）与式（9）等价。其中，G∈Rn×k，为标签矩阵，虽然描述的是聚类和样本之间的非排他性关系，但最终是通过索引标签矩阵G中每行最大元素所在列，从而确定聚类标签。并且，与G无限接近的F中元素的数值可以直接表示数据点和簇之间的关系。因此，硬聚类不需要阈值或界限值来保证硬分配。被松弛的F具有连续值，但是与谱聚类不同的是，在式（10）的模型中，F无限接近非负矩阵G。式（10）与式（9）相比其计算成本更低，且更具有可解释性。因此，将第2项用于统一标签矩阵可以降低时间成本，使该算法快速收敛。

2.2 优化

由于式（10）是一个非凸问题，因此优化过程采用交替方向乘子法（ADMM），将式（10）所提的问题分解为两个子问题进行求解。两个子问题分别是对标签矩阵G和指示矩阵F求得局部最优解。本文将最终的方法总结在下文的算法1中。

第1 步固定F并更新G。可以使用拉格朗日乘子法（Lagrange Multiplier Method）和KKT（Karush-Kuhn-Tucker）条件进行求解。虽然固定了F，但仍然需要满足条件FTF=I。通过增加和删除常数项，可以将问题转化为

从而可以进一步求解得：

则标签矩阵的最优解可以表示为

式中，（·）+表示矩阵中每个元素均取绝对值。

第2步固定G并更新F。假设(W(v)F+λF)的奇异值分解（SVD）为则式（10）可转化为

最终的方法总结如下。

2.3 初始化与构图

指示矩阵F的初始化有两种方法：第1 种，可以通过随机生成一个符合正交约束的矩阵进行；第2 种，可以通过计算的前k个最小特征值对应的特征向量构建，这种方法等价于计算W（v）的前k个最大特征值对应的特征向量。计算W（v）或并对其进行特征分解是一种十分消耗内存及时间的方法，为提升效率，可以通过奇异值分解的方法来求解。假设。若对(v)进行SVD 可得到。因为(v)的左奇异向量为W（v）的特征向量，因此，可通过计算前k个最大的奇异值对应的左奇异向量对F初始化。

FMCULM的详细流程见图5。

图5 FMCULM算法流程图Fig.5 Flow chart of FMCULM algorithm

2.4 时间复杂度

为进一步验证本研究所提算法在运行时间方面的优势，对时间复杂度进行进一步分析。随机选取锚点地址的时间复杂度为O（1），通过SVD初始化F的过程需要O（m2n+m3），构建的时间复杂度为O（mndv），迭代的过程需要O（mnk+m2k+nk2+k3）tv（其中t为迭代次数），对M进行SVD 的过程需要O（nk2+k3）。由于m＞k且n≫m，因此，总体的时间复杂度为O（m2n+mnktv），即只需要线性的时间复杂度。

3 实验

为说明本算法的有效性，本节将该算法与其他聚类算法在真实数据集上进行对比。实验中所有代码的运行环境均为Matlab R 2020a，硬件系统配置为2.60 GHz、i7-10750H CPU、16 Gbyte 运行内存、Windows 10系统。

3.1 实验设计

3.1.1 评价指标

在本文所述实验中，采用准确率（γACC）、归一化互信息（γNMI）和调整的兰德指数（γARI）3 个指标来判断该算法的性能。其中γACC和γNMI指标的区间均为［0，1］，γARI的区间为［-1，1］，三者均为数值越大则性能越佳。

如式（18）所示，γACC是指通过本方法进行聚类后获得的标签与真实标签之间匹配结果的平均聚类精度。

式中：pi为第i个样本在该算法下产生的标签，yi为真实标签；当x=y时，ϕ(x，y)=1，否则为0；map（·）用来映射预测标签与真实标签之间的不同，聚类精度将以最佳的映射结果计算。

设θ为正确的聚类标签，而θ'则为通过算法预测的聚类标签，可以通过下式计算γNMI：

式中，P(·)为该样本属于该集群的概率，P（·，·）为二者的联合概率，H（·）表示熵。

γARI用于测量两个集合之间的相似性，即

式中，和分别为第i个聚类的真实标签和学习标签，表示从a个元素构成的集合中选取b个。

3.1.2 对比算法

将FMCULM与下列9种基准算法进行比较。为加以区分，将单视图k-means 和Ncut 分别标记为Sk-means 和SNcut，二者均为单视图聚类算法。MSC 和CoregSC 是传统的多视图聚类方法，且是基于协同训练的多视图聚类方法。MkC 和multiNMF是基于多视图子空间的多视图聚类方法。ASMV、MGL和MCGL是基于加权的多视图聚类方法。由于Sk-means 和SNcut 只对单视图数据有效，所以对于多视图数据，本文将二者在每个视图中分别运行，并记录最佳性能的视图结果。

本研究从其作者的主页获得比较算法的原始代码并在MATLAB中运行。对比算法的参数设置采用对应文献中具备最佳性能的参数进行设置，以避免该方法的结果非最佳性能。对于FMCULM，也在MATLAB中运行，以确保环境的一致性。在参数设置中，利用经验将k设置为20，并将平衡系数设置为1。

3.1.3 实验数据集

本实验选取了不同视图数量、不同数据来源、不同维度的4种数据集。数据集来自于植物、新闻、手写数字和网页4类真实案例，对本研究所提算法进行多方面的比较。本文将重要参数归纳在表1中，以方便对比。表1中，n表示实例数量，v表示视图数量，c表示簇类数量，d1至d6分别表示第1个至第6 个视图的数据数量。①100leaves：有3 个视图，每个视图均为来自100 种植物叶片的1 600 个数据点。每个对象可以分别用3个视图中的形状描述符、精细比例边距和纹理直方图来描述。② 3sources：来自BBC、路透社和《卫报》均涉及的3 个视图。每个视图有169条新闻，可以分为6个簇。③Mfeat：手写数字数据集，包括来自UCI存储库的手写数字（0-9）。共计6个视图，每个视图包含2 000个样本。其中，每个样本均可以由6种不同类型的特征来表示。④ WebKB：有3个视图，其中每个视图有4类共203个网页。每个网页都可以用超类网页的锚定文本、页面的内容和标题来描述。

表1 真实数据集参数Table1 Real-world data set parameters

3.2 实验结果

实验结果比较如表2、表3和表4所示，表中结果记录为“→0”代表其结果接近于0，并非其结果实际为0。本实验将每种算法运行10次取最佳结果，以百分比的形式记录在表格中，并在表格中的括号内记录运行10次的标准差。为了方便观察，表中每个数据集中性能最佳的前两个数据加粗表示。图6和图7分别给出了图重构的实例图以及对于目标函数和平衡项收敛速度的对比图。

表2 聚类性能在准确率方面的比较Table 2 Clustering performance comparison in terms of ACC %

表3 聚类性能在归一化信息方面的比较Table 3 Clustering performance comparison in terms of NMI %

图6 正交非负约束在实例中的说明Fig.6 Practical illustrations of orthogonal non-negative constraint in the example

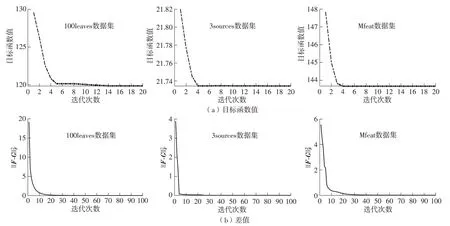
图7 在3个真实数据集中算法收敛性的分析Fig.7 Analysis of algorithm convergence in three real data sets

进一步分析FMCULM的算法性能，可以从图表中得出如下实验结果。FMCULM 在大部分数据集上达到了所列性能指标的最高聚类性能。例如，FMCULM 在100leaves 上相对于最好的第2 种MCGL的ACC超过了约11.9%，在3sources上相对于MGL的NMI 结果超过了约5.9%。FMCULM 优于其他算法的性能是由于在选取锚点时不再需要k-means 等前工程，这使得算法摆脱了选取锚点的质量对其的影响。同时，由于算法不需要后处理，而是通过直接索引标签矩阵每行最大元素所在列，从而使算法的性能得以提升［28］。此外，由于手写数字的数据集中包含大量的负值，而MultiNMF 是基于非负矩阵分解的聚类方法，因此，在Mfeat 数据集中，MultiNMF无法处理。与CoregSC和MSC等由谱聚类改进而来的多视图算法相比，FMCULM有明显的优势。这可能是由于本研究的算法不依赖于统一图的学习，而是通过统一标签矩阵获得标签。

此外，图6（a）给出了FMCULM 在100leaves 上图重构的实例说明。可以直观地看到，通过FGT重建的图具有清晰的结构，图中存在较强的簇内连接和较弱的簇间连接。结构化图重建过程使本研究的方法优于其他方法的聚类性能。如图6（b）所示，原始构造图是双随机矩阵W。对比可知，通过FGT重建的图比W具有更清晰的结构。

3.3 计算效率实验

算法的运行时间如表5所示，FMCULM 明显优于其他算法，在100leaves、3sources、Mfeat 和WebKB 数据集上均为最快的。在数据量最大的Mfeat 数据集上，FMCULM 的运行时间也明显高于其他算法，这显现出了该算法在时间成本上的优势。主要原因有3个：其一，由于本文的算法没有求解相似矩阵而是求解聚类过程中必要的值；其二，摆脱了特征值分解导致的O（n3）的高昂时间成本，转而利用SVD求解F，从而降低时间成本；其三，由于非负约束使得可解释性大幅提升，从而使得FMCULM不需要后处理。

表5 真实数据集中聚类性能在时间方面的比较Table 5 Performance comparison of each method in terms of running times s

3.4 算法收敛性验证

由于FMCULM是一种迭代算法，不可避免地要关注其收敛性。本研究还对该算法的收敛速度展开了实验。图7 中虚线显示了FMCULM 在100leaves、3sources和Mfeat 3个数据集上的收敛曲线。虚线表示目标函数值与迭代次数的关系，实线代表平衡项与迭代次数之间的关系。在实际的实验中，通常在目标函数两次迭代的变化量不大于10-4时判定为收敛。在收敛性验证的实验中，取消这一限制，强制其执行20次迭代。对于本研究中的平衡项，进行了100 次迭代的实验，从而充分验证这一方法的有效性和稳定性。FMCULM 通常是在10 次迭代之内收敛，原因是本研究为每个子问题提供了一个优化的解决方案。

FMCULM在目标函数中加入了平衡项，即统一标签矩阵，并设置了平衡系数λ。F和G在每次迭代中逐渐相互接近，表示负项逐渐趋小或消失。从式（14）可知，这正是F和G之间的差异或负数的部分。在图7 中，平衡项的值在迭代5 次左右趋向于0，这说明平衡项达到了收敛。此外，由于本研究所提出的算法是一种无监督学习方法且需要输入聚类数量，因此大大降低了快速收敛后过拟合的风险，为方法的稳定性和可靠性提供了充分的保证。

4 结语

本研究提出了一种基于统一标签矩阵的快速多视图聚类算法。该算法具有可解释性强、准确率高和运行速度快的优点。FMCULM 从谱聚类统一的切图观点出发，将构建的相似矩阵在正交和非负约束下重构为具有强簇内连接和弱簇间连接的结构图。非负约束使聚类更具有可解释性，从而避免后处理。在真实数据集上进行的大量实验表明，FMCULM 具有良好的性能。此外，由于FMCULM 在不同数据集中参数的设置主要依据经验进行调整，这导致该算法的自适应性有待提高。在接下来的研究中，将重点研究如何提高FMCULM的自适应性；此外，如何利用多视图互补信息来解决数据缺失的多视图聚类问题，也是我们后续重点关注的内容。