一种串并混联机械手的运动学分析

赵 普,何 阳,汪序凯,吉起旺,王润芝,赵裕明,冯海兵,李守军

(宿迁学院 机电工程学院,江苏 宿迁 223800)

0 引言

工业机器人是工业生产中的重要高端装备,常用的为六自由度串联机器人,多自由度串并混联机械手作为通用工业机器人的补充,在上下料、农业采收等领域突显其优势,广泛应用于机械制造、石油化工和农业采收等行业。目前,串联机械手的研究理论已经较为成熟,制造工艺也较为先进,形成一种以企业研发制造为主体的成熟的发展模式[1-3]。近年来,串并混联机械手逐渐引起了科研工作者和企业的重视,其研究和应用也在快速发展[4-7]。

一种串并混联机械手[8]由大臂、中臂、小臂和末端执行器组成,并且在大臂、中臂及小臂中的平面双菱形机构中均采用液压驱动方式,以保证良好的承载性。本文利用D-H法对该机构进行位置分析。

1 机械手构型介绍

7自由度串并混联机械手由机架、大臂、中臂、小臂和末端执行器组成,如图1所示。大臂为并联机构,其中两个移动副P1、P2为驱动;中臂为平行四边形机构,其中P3移动副为驱动;小臂为串并混联机构,其中两个移动副P4、P5和两个转动副R7、R19为驱动。

图1 串并混联机械手机构简图

设该机械手机构的主要几何参数为:S11S12=l1,S21S22=l2,R1R2=l3,R10R11=l4,R9R12=l5,S11S21=2u1,PS12=PS22=u2,BC=u3,UA-S21C=u4,ER1=u5,EF=u6,FR3=u7,R2R3=u8,UP=u9,UD=d1,DF=d2,R4R5=d3,GR7=d4,R7R8=d5,R8R9=R8R10=e1,R8R11=R8R12=e2,R8R13=e3,R15R16=e4。

2 机械手位置正解分析

由图1可知,该机械手的机构较为复杂,为了简化计算,可以根据各关节运动特点将其等效为串联机构,如图2所示,其中RU1和RU2分别与图1中U副的两个转动副,P45与图1中P4和P5等效,R4和R5分别与平行四边形R3R4R5R6中边R4R5两端的转动副对应,且转动副R4和R5的转角之和时刻为零,其余运动副与图1中对应。

2.1 坐标系建立

利用D-H法在每个关节处建立连杆坐标系,如图2所示,与机架固定的坐标系为基坐标系{O0}(原点与虎克铰中心重合),与连杆i固连的坐标系称为坐标系{Oi}(i=1～7),坐标系{O0}与坐标系{O1}的原点重合,坐标系{O7}为与末端执行器固连的坐标系。

图2 机械手等效机构

2.2 位置正解

根据D-H参数法,列出各连杆对应的连杆参数见表1,ai表示连杆长度,m;αi表示连杆扭角,(°);di表示相邻连杆之间的距离,m;θi表示相邻连杆之间的转角,(°)。

表1 等效机构的连杆参数

续表1

基于上述连杆参数,利用D-H法建立各连杆之间的变化矩阵Ti(i=1～7)得

Ti=Rot(z,θi)Trans(ai,0,di)Rot(x,αi)

(1)

式中,s表示sin,c代表cos。

由此可得机械手末端坐标系{7}相对与基础坐标系{0}的位姿变换矩阵为

(2)

机械手末端执行器的姿态用欧拉角表示,绕z轴转角α,绕y轴转角β,绕z轴转角γ,则欧拉变换矩阵为

(3)

由于式(2)与式(3)相等,即可得到串并混联机械手的姿态表达式。

2.3 位置反解

令式(2)与式(3)左右两边矩阵的(3,3)元素相等可得

(4)

由式(2)与式(3)相等可得

E(T5·T6·T7)-1=T1·T2·T3·T4

(5)

分别令式(5)左右两边矩阵的(1,4)、(2,4)和(3,4)元素相等,可解得θ1,θ3和l。

又由于R4R5为平行四边形的一边,则有关系

θ4=-θ3

(6)

再对式(3)进行变化,可得

(T1·T2·T3·T4)-1E(T6·T7)-1=T5

(7)

令式(7)左右两边矩阵的(1,1)元素相等,可解得θ5。

2.3.1 大臂位置反解

如图1所示,建立固定坐标系{U}:U-x0y0z0,其中坐标原点与虎克铰中心点U重合,z0轴与虎克铰靠近基座的转轴轴线重合,x0轴与虎克铰远离基座的转轴轴线重合,y0轴的方向由右手定则确定;建立参考坐标系{P}:P-xcyczc,其中坐标原点P位于球副S12和S22连线的中点,x1轴的方向为沿球副S12和S22连线方向,z1轴的方向与z0轴方向相同,y1轴的方向由右手定则确定。

大臂的位置反解即为求解θ1和θ2与l1和l2之间的关系。参考坐标系{P}相对于定坐标系{U}为先绕z轴旋转θ1,再绕x轴旋转θ2所得,其旋转矩阵可表示为

R=Rot(z,θ1)·Rot(x,θ2)

(8)

设球副S11和S21中心点在固定坐标系中的位置矢量为S11和S21,球副S12和S22中心点在参考坐标系中的位置矢量为S120和S220,均为已知量。由坐标变换可得球副S12和S22中心点在固定坐标系中的位置矢量为

S12=R·Si20+U,i=1,2

(9)

式中,U为虎克铰中心点U在{U}坐标系中的位置矢量,为已知量。

根据大臂机构的几何关系,得矢量方程为

li=Si2-Si1,i=1,2

(10)

式中,l1为大臂的两个驱动杆长矢量。

2.3.2 中臂位置反解

设中臂的驱动杆长为l3。中臂的位置反解即为求解θ3或θ4与l3之间的关系。

由图3可知,在三角形FR3R2中,有关系式

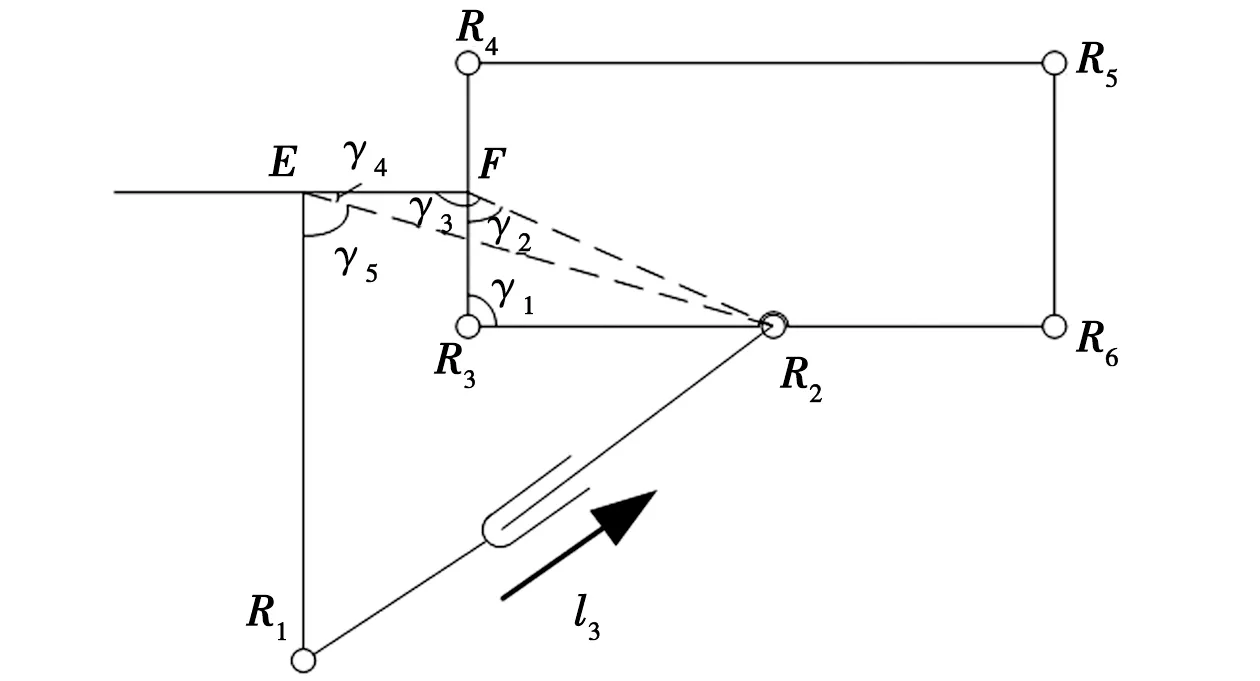
图3 中臂机构示意图

(11)

在三角形ER2F中,有关系式

(12)

在三角形ER1R2中,有关系式

(13)

联立式(11)～式(13),即可求得l3。

2.3.3 小臂位置反解

由于小臂机构的转动副R7和R19的转角分别与等效机构中的θ5和θ7相同,可由式(4)和式(7)获得。因此小臂的位置反解主要为求解θ6和l与l4和l5之间的关系。如图4所示为小臂机构的示意图。

图4 小臂机构示意图

由图4中各杆件长度有如下关系

(14)

如图4所示,在ΔR8R10R11和ΔR8R9R12中,已知R8R9、R8R10、R8R11、R8R12和φ1、φ2,l4和l5可以通过余弦定理解得。

3 结论

本文针对一种7自由度串并混联机械手,采用部分机构等效简化的方法,对机械手原型机构进行了运动学分析,得到了机械手的位置正反解。该机械手采用外伸悬臂结构,且具有7个独立的自由度,在合理设置驱动的前提下其工作空间较大、末端灵活性较好。基于上述特点该机械手特别适合作为工业上下料机械手或农业采摘机械手。本文的研究为该机械手的进一步研究奠定了基础。