全长锚固锚杆支护软岩巷道围岩承载结构力学响应解析

王想君，李英明，赵光明，孟祥瑞，王 艺，程 详,3

（1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001；2.安徽理工大学 矿业工程学院,安徽 淮南 232000；3.安徽理工大学 采矿工程博士后流动站,安徽 淮南 232000）

0 引言

深部软岩巷道开挖-支护过程中，围岩-支护体系统协同作用承载机制一直是理论和工程实践研究的重点[1-3]。开挖扰动打破了原有的应力平衡状态，围岩卸荷和应力重分布使其发生变形破坏并形成新的承载结构[4-5]。同时，为了保证围岩承载结构的稳定性，要求锚杆、索等构件须具备支护时效性，即能够明显改善围岩周边的力学环境及行为，有效抑制其变形破坏发展，从而迅速提高围岩自身的承载能力[6-7]。在巷道围岩-支护体相互作用过程中，围岩应力分布特征、锚杆受力规律以及两者间的相互作用关系是不可分割的有机整体，国内外学者对此进行了深入探讨，并取得大量研究成果。

在巷道围岩应力分布方面，最早由Fenner 和Kastner 等通过对轴对称圆巷的理想弹塑围岩介质进行力学分析，得到了经典的围岩塑性区半径和应力解，并一直被业界沿用至今[8-9]。陈登国[10]、余涛[11]等将围岩和锚杆相互作用承载体系视作锚固承载层，并分析了其应力分布特征。但是随着煤矿开采深度的增加，巷道软岩性质表现的愈发突出[3,12]，付国彬[13]、马念杰[14]认为，当岩体的应力超过其极限抗压强度后，岩体自身强度会随着塑性应变增加而逐渐衰减，并建立了巷道围岩塑性软化力学模型，将其由表及里依次划分为破碎区、软化区及弹性区。赵光明等[1]基于统一屈服准则，将软岩巷道围岩划分为“锚网喷区”和“非锚网喷区”，并分析了围岩承载结构力学特征。周建等[15]对圆形硐室围岩在考虑锚固和空间效应条件下进行了弹塑性分析，获得了围岩应力与变形解。同时，《煤矿安全规程》第四十四条规定软岩使用锚杆支护时，必须全长锚固[16]。全长锚固锚杆能在一定程度上避免锚固界面层的脱黏失效问题，可沿锚杆全长对围岩产生锚固作用[17]，对围岩应力分布具有显著影响。因而在全长锚固锚杆受力特征方面，学者们针对锚杆承载特性进行了大量的拉拔试验及理论研究[18-20]，获得了杆体在拉拔过程中剪应力和轴力的非均匀分布特性，但是拉拔试验难以准确反映杆体在实际支护过程中的受力情况及其作用机制。FREEMAN[21]、王明恕[22]等通过现场实测提出了中性点理论，为全长锚杆支护力学分析奠定了基础。CAI 等[23]基于载荷传递微分方程，提出了一种锚杆轴向力的预测方法。姚显春[24]、朱训国等[25]认为锚杆剪应力是由围岩变形产生的剪应力和锚杆近端剪应力对锚杆远端拉拔产生的剪应力两部分组成，并建立了全长锚杆的应力分布函数。陈梁等[26]基于剪切滑移模型和中性点理论，对围岩峰后剪胀变形条件下的全长锚杆受力分布规律进行了系统研究。综上所述，现有研究一般将支护体的工作阻力做了一定简化，即等效为在巷道表面均匀分布的径向支护力，而这一条件比较适用于端部锚固；并且在描述围岩-锚杆相互作用时更多的是一种处理方法或者相互作用结果的描述，而非相互作用本身。此外，侯公羽等[27]对弹塑性变形条件下的围岩-支护相互作用全过程进行了解析，认为在巷道开挖面空间效应影响下，围岩的虚拟支护力和混凝土(或钢架)的支护反力存在此消彼长的过程。笔者基于侯公羽的思想，认为全长锚杆作为具有延伸性能的支护构件，在其工作时不仅具有相同力学机制，且围岩力学状态也在随之发生相应变化，即虚拟支护力、锚杆受力及围岩应力分布三者处于同步动态演化状态，目前对这方面的研究鲜有报道。鉴于此，有必要对软岩巷道围岩与全长锚固锚杆的相互作用机制进行深入研究。

因此，笔者在前人研究的基础上，根据全长锚固锚杆受力边界条件，建立软岩巷道围岩变形作用下的全长锚固锚杆力学模型，推导了锚杆受力解析式，且将锚杆轴力以附加体积力的形式作用围岩内部。在此基础上，结合空间效应下的虚拟支护力影响与软岩三阶段力学模型，量化分析巷道在开挖-支护过程中围岩应力分布特征及锚杆受力规律，并借此揭示全长锚固锚杆与围岩耦合作用机理。研究成果可为高应力软岩巷道的全长锚固锚杆支护技术及设计方面提供一定理论依据。

1 巷道全长锚固围岩力学模型

1.1 力学模型与基本假设

建立全长锚杆锚固围岩力学模型如图1 所示。为了便于分析，对巷道全长锚固围岩模型作适当简化和假设[13]：①巷道轴向无限长，可简化为平面应变问题；②巷道为圆形，半径为直墙半圆拱(或矩形)巷道的当量半径r0；③巷道处于静水压力场中，原岩应力大小为p0；④围岩为均质、各向同性连续介质；⑤巷道周边围岩产生残余区和塑性软化区；⑥全长锚固锚杆沿巷道断面径向均匀分布，且将围岩受到的锚杆支护力简化为轴对称的径向体积力[1,10]。

图1 全长锚杆锚固围岩力学模型Fig.1 Mechanical model of full-length bolt anchoring surrounding rock

1.2 全长锚固锚杆受力分析

巷道开挖后即时进行支护，锚杆不仅随着围岩变形发展产生整体移动，而且由于围岩径向各点的位移量不同以及杆体与岩体刚度的非协调性，致使围岩/杆体界面层产生剪应力，且沿锚杆全长剪应力分布呈现非均匀性。假定锚杆、锚固剂(或砂浆)和岩石黏结良好，在图1 中取一全长锚杆锚固单体，沿该单体轴向取一微单元进行力学分析，如图2 所示。

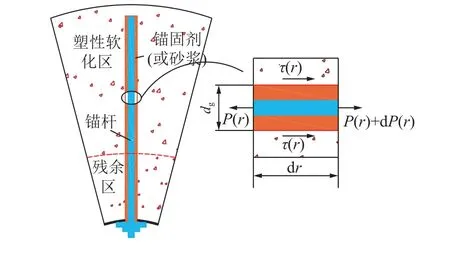
图2 围岩中全长锚固锚杆微单元受力示意Fig.2 Stress components of full-length anchor element in surrounding rock

根据锚杆轴力与围岩/锚固剂(或砂浆)界面剪力(简称界面剪力)的平衡关系，围岩变形作用于杆体单位长度上的剪力为

式中：P(r)为锚杆轴力；T(r)、τ(r)分别为r点处界面剪力和剪应力；dg为钻孔直径。

假设锚杆与孔壁之间没有产生明显相对滑动，即锚杆与围岩体的变形近似满足以下变形协调条件[28]

式中：Ub为锚杆杆体的变形量；Us(r)为锚杆支护条件下围岩的实际位移。

假定无锚杆支护条件下的围岩位移U(r)与有锚杆支护条件下围岩的实际位移Us(r)之差为

式中：U(r)通过弹塑性计算或现场测量拟合得到。

式(4)中F(r)精确表达式取为如下幂级数的形式[28]

需要说明的是，在锚固设计中，一般将岩体和锚固剂(或砂浆)界面的剪切强度作为确定锚固长度的基本依据[29]，并且现场拉拔试验也表明围岩/锚固剂(或砂浆)界面更易于发生脱黏失效[30]。因此，把锚杆和锚固剂(或砂浆)视为一个整体，同时由于围岩变形通过锚固剂(或砂浆)介质传递给杆体，考虑到两者的变形协调，在计算分析过程中采用锚杆和锚固剂(或砂浆)整体的综合弹性模量Ea，其计算公式[29]为

式中：Eb、Eg分别为锚杆和锚固剂(或砂浆)的弹性模量；Aa、Ab、Ag分别为钻孔、锚杆和锚固剂(或砂浆)的横截面积，Ag=Aa-Ab。

假定全长锚固锚杆支护过程中始终处于弹性状态，即杆体的变形为完全线弹性，则根据虎克定律有

式中：εa为锚杆轴向应变。

将式(8)代入式(1)得界面剪力为

根据式(8)、式(9)可知，要得到全长锚固锚杆受力的具体表达式，必须求解巷道围岩径向位移，但其位移比较复杂。通常软岩巷道开挖后，围岩会产生大规模的塑性破坏，变形剧烈，文献[31]通过考虑软岩峰后强度的应变软化和体积扩容特性，将围岩由表及里依次划分为残余区、塑性软化区及弹性区。本文假设锚杆全长处于围岩残余区和塑性软化区内，则圆形巷道轴对称的径向位移[31]为

联立式(10)、式(6)并代入式(8)、式(9)得到全长锚固锚杆的轴力和界面剪力为

试验研究表明[17]，全长锚杆锚固时轴力随着围岩碎胀变形先后经历由增大到迅速减小、再到逐渐丧失的过程，文献[28]分析了全长锚固锚杆在正常支护和临界失效两种工况下的受力特征。本文仅考虑锚杆轴力未丧失即锚杆正常支护时的受力情况，围岩变形条件下的全长锚固锚杆剪应力分布情况如图3 所示。

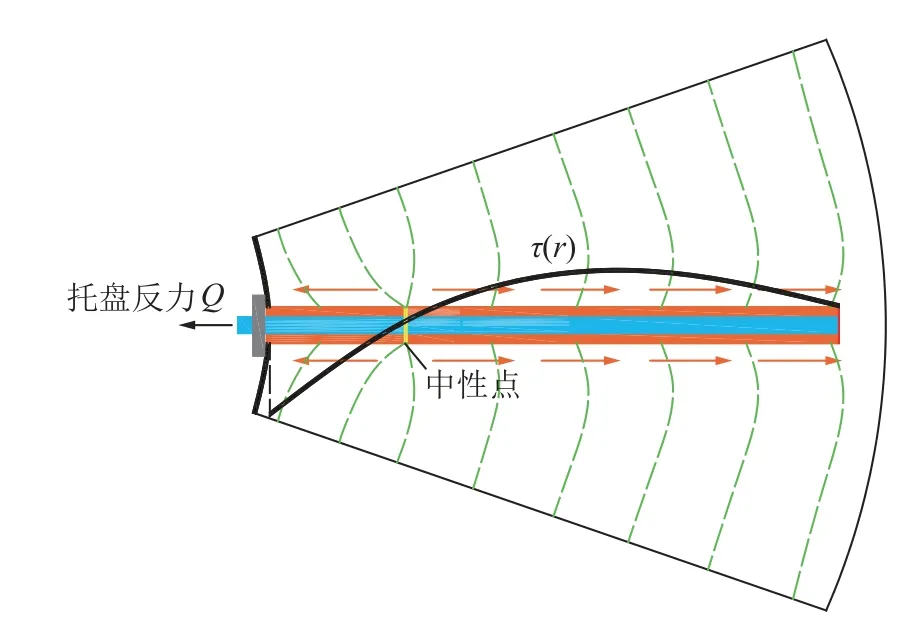
图3 全长锚固锚杆正常支护下的剪应力分布情况Fig.3 Shear stress distribution of full-length anchoring bolt under normal support

对于图3 中全长锚固锚杆正常支护时的受力情况，其边界条件为

式中：r1为孔口到中性点的距离；L为全长锚固锚杆的长度。

将式(13)代入式(11)，式(12)，求解得到系数为

由式(1)和图3 可知，锚杆在界面剪力T(r)和托盘反力Q作用下的静力平衡条件为

将m2，m3，m4代入式(11)、式(12)，并联立式(14)可求解得到锚杆中性点的位置r1，进而联立式(1)获得全长锚固锚杆在正常支护工况下其轴力和界面剪应力的解析解。

1.3 全长锚固锚杆支护围岩的体积力模型

如前所述，全长锚固锚杆支护过程中，围岩变形驱动锚杆杆体表面产生剪应力，使锚杆受到轴向拉伸作用；由于力的作用及反作用，锚杆通过锚固剂(或砂浆)会抑制围岩产生过大变形，从而给围岩提供支护抗力，起到支护围岩的作用。因此，锚杆与围岩的相互作用是一个不断收敛平衡直至形成稳定承载系统的过程。

全长锚固锚杆-围岩楔形单元体(图4)的体积为

图4 全长锚固锚杆-围岩楔形单元体Fig.4 Wedge element of full-length anchoring bolt and surrounding rock

式中：D1、D2为锚杆的间、排距。

楔形单元体受到的径向体积力K(r)为

联立式(11)、式(15)和式(16)得到楔形单元体的体积力表达式。

2 巷道围岩弹塑性分析

2.1 围岩力学模型

由于软岩巷道围岩径向各点的力学行为与岩石的全应力-应变曲线3 阶段(弹性、塑性软化及残余强度阶段)相对应[4,9,13]，因而将图1 表示为如图5 所示的力学模型。锚杆支护后在围岩产生的附加应力场会改善其应力状态，故将支护后的围岩进一步划分为锚固残余区、锚固塑性软化区、非锚固塑性软化区和弹性区。

图5 软岩巷道围岩分区模型Fig.5 Model of surrounding rock partition of soft rock roadway

此时，非锚固区和锚固区的静力平衡方程[32]为

式 中：ɛr、ɛθ分别为围岩的径向和切向应变。

2.2 巷道开挖面空间效应理论计算

巷道开挖过程中，开挖面附近的岩体由于自身的空间效应(一般指距开挖面(5～6)r0以内)，导致围岩变形及应力重分布不能立即完成，可等效为在巷道周边存在虚拟支护力的作用，该效应为巷道及时支护提供了理论依据[1]。虚拟支护力作用下的围岩位移一般由E.Hoek 拟合现场测量数据给出的方程[27]来计算：

2.3 围岩应力分析

2.3.1 弹性区

由胡克定律可以得到弹性区的应力场[31]为

2.3.2 塑性软化区

1)非锚固塑性软化区。假设巷道围岩峰后塑性软化阶段的岩体强度σs是其应变ɛθ的线性函数，则σs可表示[33]为

塑性软化区的Mohr-Coulomb 强度准则为

联立式(17)中第1 式、(22)和式(23)，并当r=Rs时，由应力连续求得塑性软化区的径向应力为

2)锚固塑性软化区。联立式(17)中第2 式和式(24)，并由锚固软化区和非锚固软化区应力连续条件，即当r=r0+L时，求得锚固塑性软化区径向应力为

2.3.3 残余区

1)非锚固残余区。残余区Mohr-Coulomb 强度准则为

在巷道表面r=r0处，将锚杆提供的支护阻力pi代入式(28)、式(29)，并联立式(25)可分别得到锚固前、后的残余区和软化区半径。

综合上文分析可知，由于考虑因素较多，所以计算过程较为复杂，其计算步骤主要如下：①首先求解巷道无支护(此时相当于围岩应力完全释放，初始支护力px=0)时围岩的残余区和软化区半径(Rb、Rs)，然后将其联立式(10)、式(19)求得空间效应影响下的巷道表面位移，再将该位移代入式(10)、(28)反算得到不同滞后开挖面距离x下的巷道表面虚拟支护力px；②在考虑虚拟支护力条件下，将围岩位移差(无支护和开始支护时的围岩位移差)代入全长锚固锚杆受力解析式，求解得到全长锚固锚杆轴力；③最后根据锚固后的围岩应力表达式及边界条件得到巷道围岩各分区的半径及应力分布。

3 算例分析

以淮南某矿轨道大巷工程背景为例，取巷道当量半径r0=3.0 m，原岩应力p0=24 MPa，岩体弹性模量E=8.0 GPa，泊松比ν=0.27，围岩极限强度σq=11.8 MPa，残余强度=0.52 MPa，内摩擦角φ=28°，其中待定常量的取值范围[33]是：扩容系数n1，n2=1.15～1.55，应变软化系数α=3.5～4.3(取4.1)。全长锚固锚杆的弹性模量Eb=200 GPa，直径db=22 mm，长度L=2.6 m，锚杆间排距D1，D2=0.8 m，托盘反力Q=25 kN。锚固剂弹性模量Eg=16 GPa，钻孔直径dg=32 mm。

3.1 围岩承载结构力学分析

巷道开挖卸荷使围岩由三向应力状态快速转变为二向(或单向)应力状态，围岩内部随着切、径向应力急剧升、降使其受到的偏应力作用骤增，裂隙向巷道周边快速萌生、扩展，导致围岩不断屈服进入塑性状态并形成新的承载结构[34]。同时，由于巷道开挖面空间效应，围岩径向应力没有得到充分释放，致使围岩破裂损伤及应力重分布不能立即完成[27]，具体应力表征如图6a 所示。当滞后开挖面距离x=2.0 m时，切向应力峰值距洞壁约3.79 m 为38.39 MPa，而当x增加至15.0 m 时，塑性区厚度增加了69.92%。说明随着滞后开挖面距离增加，围岩径向应力明显降低，切向应力峰区向其深部转移，表明一定径向范围内各点的围岩强度不断劣化，塑性屈服范围显著变大，导致围岩自身承载能力大幅减弱。主要原因在于随着开挖面向前推进，巷道自身的空间约束效应不断解除，即虚拟支护力逐渐衰减直至消逝，使得围岩变形破坏加剧。由此可见，软岩巷道围岩应力及强度调整过程可分为两个阶段，如图6b 所示，第Ⅰ阶段可近似认为在巷道开挖快速完成，具有不可控性；第Ⅱ阶段围岩的变形破坏随径向应力释放呈现渐进式发育规律，同时也是围岩-支护体相互作用且产生协同承载效应的重要阶段。

图6 无支护条件下空间效应对围岩应力的影响Fig.6 Influence of spatial effect on surrounding rock stress under unsupported condition

国内学者关于软岩巷道围岩承载效应相继提出了“主次承载区”、“深浅支撑层”等概念[35-36]，尽管提法各异，但其内涵基本一致，都是以围岩破坏程度及其应力分布情况作为划分依据。次承载区一般为残余区，所受切向应力要低于原岩应力，主承载区通常由塑性软化区和弹性区组成，承担了绝大部分的围岩载荷，且对巷道稳定状态起着决定性作用。主承载区越靠近洞壁，围岩稳定性越高，反之越低[35]。综上可知，巷道支护本质是及时有效地抑制围岩切向应力峰值区从A向B偏移(图6b)，减少围岩在第Ⅱ调整阶段的能量消耗，使其在较高能量状态下达到平衡状态，故可将AB区间视为“锚固调控区”。该区的力学机制如下：在围岩第Ⅰ调整阶段(图6b曲线1)及时将锚杆置入并涵盖次承载区，之后锚杆在第Ⅱ调整阶段的弹塑性及剪胀变形驱动下产生锚固力，并反作用于围岩。在此过程中，围岩的虚拟支护力和锚杆锚固力处于此消彼长的状态，但由于二者在量级和敏感性方面的差异，应力曲线1 存在向曲线2 转化的趋势，直至达到平衡稳定状态为止。这反映了锚杆支护具有显著的时效性特征，也说明了围岩与锚杆之间不仅要满足锚固耦合效应即产生耦合作用力，同时还要充分发挥围岩主、次承载区的相互协调作用，提高围岩自身的承载能力，使巷道锚固系统整体趋于稳定。

3.2 全长锚固围岩承载结构力学特性研究

围岩与锚杆相互作用过程中，锚杆在不同深度围岩的不均匀变形驱动作用下产生“锚固效应”，从而达到约束围岩变形、抑制其破坏的目的。这说明锚杆“锚固效应”强弱不仅和其长度、直径等属性密切相关，同时还受到围岩破坏程度、扩容特性等客观条件的影响。本节基于全长锚固围岩模型的理论推导，研究空间效应(支护时机)、扩容系数、锚杆长度和托盘反力对围岩-锚杆相互作用的力学特性的影响。

3.2.1 空间效应对围岩应力和锚杆受力的影响

图7 为不同滞后距离支护(支护时机)对围岩应力及锚杆轴力分布的影响。由图7 可知，随着滞后开挖面支护距离的减小，围岩应力升高区向洞壁方向移动，残余区和塑性软化区半径不断缩小，与此对应，锚杆杆体所受轴力呈现愈发不均分布趋势，轴力峰值明显升高。其中，滞后开挖面距离x为2.0、4.0和6.0 m 时，对应的残余区和塑性软化区外边界分别为：1.32r0/2.59r0、1.38r0/2.72r0、1.44r0/2.83r0，锚杆所受轴力峰值分别为141.38、100.73、68.96 kN。与无支护时(x=15.0 m)相比，残余区范围降低27.1%～47.0%，塑性软化区范围降低9.8%～17.4%。由此可见，巷道开挖-支护过程中，锚杆安装时机越早，围岩-锚杆的耦合作用效果就越显著，二者之间能快速构成共同承载体，不仅提高了围岩的自承能力，减小了塑性区范围，还有效发挥了锚杆的锚固潜能，符合上述“锚固调控区”的概念。

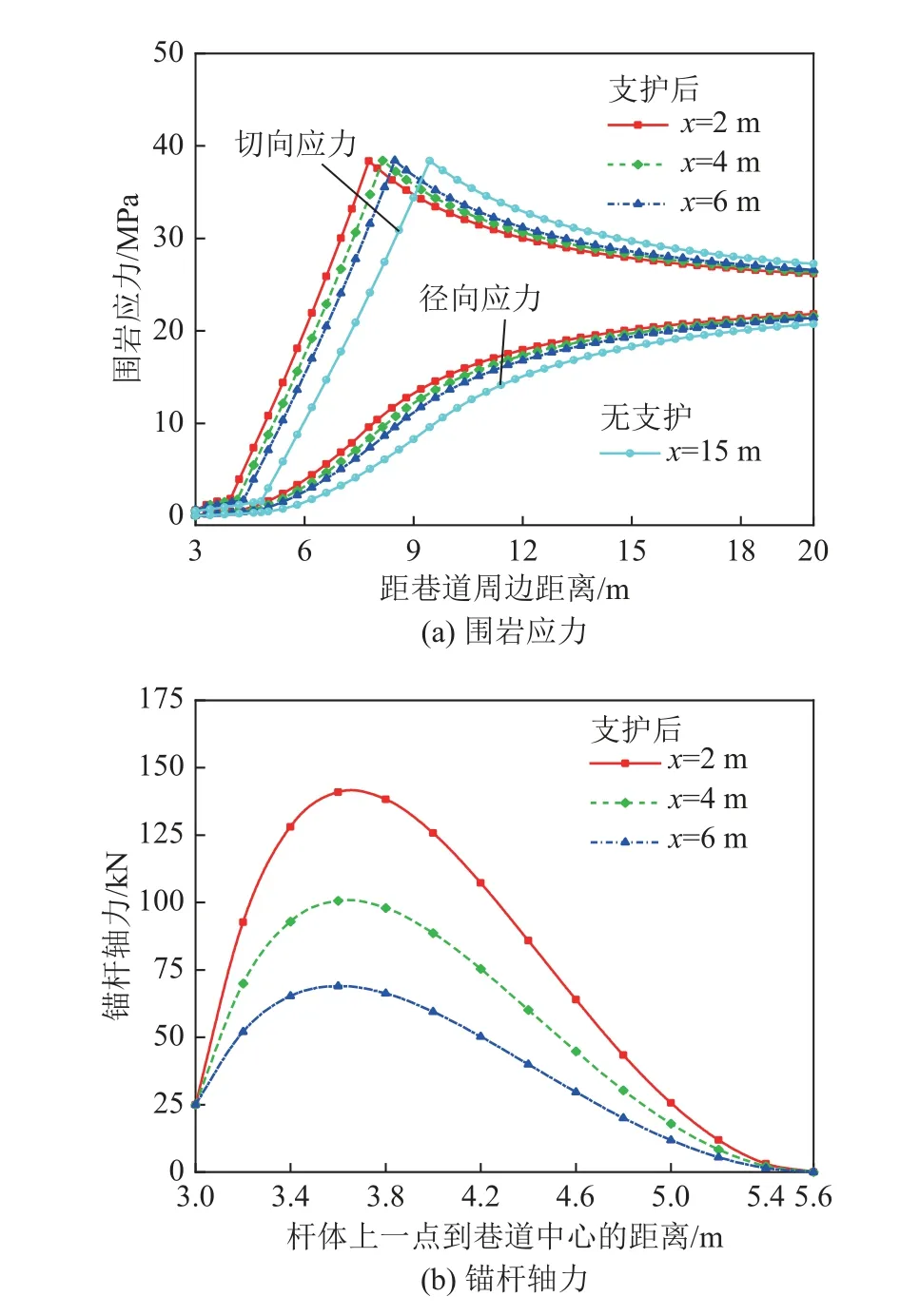
图7 空间效应与围岩应力、锚杆轴力关系Fig.7 Relationship between space effect and surrounding rock stress and axial force of anchor rod

3.2.2 扩容特性对围岩应力和锚杆受力的影响

以滞后开挖面3.0 m 为研究断面(下文保持相同)，得到开挖面推进过程中围岩扩容系数对围岩应力和锚杆受力的影响，如图8 所示。由图8 可知，围岩残余区扩容系数n2与锚杆轴力分布呈正相关性，而与围岩切向应力峰值位置呈负相关性，即随着扩容系数增大，锚杆轴力集中程度明显升高，围岩塑性区半径不断减小。其中，当扩容系数n2为1.4、1.6和1.8，锚杆轴力峰值为127.22、165.4、211.57 kN，则所对应的残余区和塑性软化区外边界分别为：1.34r0/2.63r0、1.29r0/2.52r0、1.23r0/2.41r0。经过分析，原因在于扩容系数越大，围岩位移及其梯度变化明显增高，致使围岩/锚固剂界面间相对位移变大，锚杆轴力迅速升高，进而对围岩的产生的锚固作用愈显著。这表明较破碎围岩的扩容(剪胀)变形使得锚杆锚固力发展速率加快，对围岩径向应力恢复作用越加明显，有利于保证承载结构的稳定性。

图8 扩容系数与围岩应力、锚杆轴力关系Fig.8 Relationship of expansion coefficient with surrounding rock stress and anchor rod axial force

3.2.3 锚杆长度对围岩应力和锚杆受力的影响

图9 给出了锚杆长度对围岩应力和锚杆受力的影响。

图9 锚杆长度与围岩应力、锚杆轴力关系Fig.9 Relationship between anchor length,surrounding rock stress and anchor axial force

可以发现，锚杆长度对围岩应力分布影响显著。锚杆长度L分别为2.4、2.8 和3.2 m 时，围岩残余区和塑性软化区外边界分别为1.38r0/2.70r0、1.33r0/2.60r0、1.28r0/2.51r0，锚杆轴力峰值分别为107.44、133.48、159.74 kN。这是因为全长锚杆锚固过程中，主要由岩石或锚杆位移引起锚固层界面的剪切使杆体产生高径向应力，通过这些应力在锚固界面产生的摩擦阻力来限制围岩变形。由于围岩变形向深部呈现逐渐衰减趋势，导致沿杆体分布的剪应力方向相反，即杆体上存在中性点，而中性点两侧剪应力使锚杆处于一种类似拔河的状态[22]。因而，锚杆长度越大，围岩与锚固剂(或砂浆)界面间的粘结范围越广，致使杆体受到的拉拔矛盾愈显著，沿杆体的轴力集中程度及其峰值相对增加，从而对围岩产生锚固作用也就越强，造成围岩应力升高区呈现向洞壁偏移的现象。同时，随着锚杆长度增加，杆体更易伸入到围岩深部较稳定的岩体中，有效锚固长度变大，而且锚固区域内的围压较大，有利于发挥锚杆的锚固性能，并能调动深部围岩实现共同承载。可见，在一定程度上锚杆越长，围岩塑性破坏范围明显减小，有助于实现巷道的长期稳定性。

3.2.4 托盘反力对围岩应力和锚杆受力的影响

图10 为托盘反力对围岩应力和锚杆受力的影响。由图10a 可知，托盘反力Q由20 kN 变化至80 kN时，相对于Q=20 kN，围岩切向应力峰值仅向巷道周边偏移了2.8%～5.3%，说明全长锚固锚杆托盘反力对控制围岩变形破坏十分有限。观察图10b 得到，随着托盘反力不断增大，沿杆体的轴力分布越不均匀，轴力明显增加，且轴力峰值位置向着孔口方向移进，说明托盘反力可以有效提高锚杆的锚固力。在该算例中，托盘反力的增幅为30 kN，但轴力峰值增幅相对较小约17 kN，根据姚显春[24]和张玉军[37]等人的观点，将单根锚杆的最大轴力等效为巷道表面的支护力，说明此时等效支护阻力变化较小，因而对围岩塑性区控制效果不明显。综上分析可知，带托盘全长锚固锚杆对围岩的锚固力由2 部分组成，一部分是托盘反力对孔口附近围岩产生压应力，并在之后的围岩变形中逐渐增大，进一步约束巷道表面，同时也对锚杆产生明显拉拔效应，改善杆体的受力状态，称之为托锚力；另一部分是杆体在围岩位移驱动作用下产生的剪切作用力即锚固界面剪应力，随着围岩位移增大而增大，使锚杆承受轴向载荷，并且由于剪应力沿杆长各点均对围岩产生锚固作用，相比于端锚而言锚固范围更广，可将其称之为剪锚力。由此可见，全长锚杆锚固过程中，剪锚力对围岩的锚固控制效果起主导作用，托锚力主要具有增强锚杆锚固力、挤压破碎松动块体的护表能力。

4 结论

1）考虑巷道围岩峰后强度软化时的扩容特征，以围岩变形为基础，结合全长锚固锚杆受力边界条件，推导了全长锚固锚杆受力解析式。利用等效体积力法建立了全长锚固围岩力学模型，将圆形巷道由表及里依次划分为锚固残余区、锚固塑性软化区、非锚固塑性软化区及弹性区，推导了围岩各分区的应力解析表达式。分析了空间效应、扩容系数、锚杆长度等因素影响对锚杆-围岩相互作用的力学响应，阐明了其耦合作用机制。

2) 巷道开挖过程中，开挖面附近一定范围内围岩的应力和强度的调整都将受到其自身的制约，其变形破坏并不会立即完成，将其划分为Ⅰ、Ⅱ两个调整阶段，锚杆锚固力主要在第Ⅱ调整阶段的弹塑性及剪胀变形作用下产生，且虚拟支护力和锚固力呈现此消彼长的状态，借此提出了“锚固调控区”的概念。

3) 锚杆安装时机越早，其杆体轴力明显增大，对围岩的破坏抑制效果越好；当围岩扩容系数较大，锚杆锚固力发展速率显著升高，有利于快速恢复浅部围岩径向应力；随着锚杆长度增大，围岩应力升高区向洞壁方向移动，塑性区半径明显减小；全长锚固锚杆托盘反力变化对围岩切向应力峰值的影响较小，其作用主要体现在改善杆体受力情况，并对破碎围岩产生一定的挤压护表能力。