考虑轴向应力影响的圆形巷道围岩塑性区边界近似解

刘洪涛，韩子俊，郭晓菲，周光东，韦晟杰，韩 洲，陈小港，程文聪

（1.中国矿业大学(北京) 能源与矿业学院,北京 100083；2.煤炭行业巷道支护与灾害防治工程研究中心,北京 100083）

0 引言

在煤炭开采过程中，巷道顶板灾害防治依然是煤矿安全的重点和难点。在2021 年全国煤矿事故统计中，顶板事故起数及遇难人数分别占煤矿事故总数的31%和32%。顶板灾害的发生是由于围岩产生不同形式和范围的破坏所致[1-2]。因此，研究巷道围岩破坏范围及塑性区分布规律对巷道围岩的稳定控制具有重要意义。

地下围岩在自重应力状态下处于稳定状态，巷道开挖会使围岩应力产生重新分布，当某一点的区域应力集中程度大于其弹性界限值时，该点处岩体会产生屈服或破坏[3]。因此选用合理屈服与破坏准则对研究地下工程问题是非常重要的。马念杰、赵志强等[4-5]基于M-C 准则，利用弹塑性力学理论推导出非均匀应力场下的圆形巷道围岩塑性区边界八次隐性方程。尹光志等[6]通过对比M-C、Mises、D-P、MLC、SMP 准则，对各种准则的适用性进行了评析，证明了MLC 准则在真三轴应力条件下的良好适用性。侯公羽等[7]基于Levy-Mises 本构关系和Hoke-Brown 屈服准则，推导出轴对称圆孔在理想弹塑性条件下的塑性解。师皓宇等[8-9]基于平面应变问题，结合三维应力场下的M-C 准则，阐述了中间主应力作用下巷道围岩的屈服破坏状态及规律，并对不同应力准则下的蝶叶敏感性进行了分析。

此外，地下工程破坏问题是弹性力学中的三维应力问题[10]。诸多学者在研究该问题时采用平面应变问题进行处理，但研究表明，巷道轴向应力对巷道围岩的变形与破坏也具有重要影响[11]。赵洪宝等[12]对三向非等压应力场下的围岩偏应力及应变能密度分布进行了研究，并结合弹塑性理论推导出圆孔周边最大、最小偏应力的计算式。尹光志等[13-14]、施维成等[15]采用控制变量的方法通过真三轴试验研究了球应力、偏应力及Lode 角对岩石变形特性的影响。骆开静等[16]以Lode 参数为指标分析了中间主应力对围岩塑性区尺寸的影响，并表明中间主应力会表现出“强烈区间性”。

综上所述，众多学者针对围岩的塑性区边界问题展开了大量研究，并基于不同岩体破坏准则推导出圆形巷道塑性区半径的弹塑性近似解，这些研究对分析巷道围岩的塑性破坏问题具有重要意义。而在探究孔洞塑性区边界问题过程中，大多数分析成果均忽略了巷道轴向应力的影响，而上述众多研究成果表明巷道轴向应力对围岩的稳定性具有重要作用。因此，基于Mohr-Coulomb 准则，通过引入Lode角，推导出考虑轴向应力作用的圆形巷道围岩塑性区边界隐性方程，得出不同三向应力条件下的围岩塑性区尺寸及形态，通过数值模拟进一步说明了理论分析的可靠性，为巷道围岩的塑性破坏分析及稳定控制提供一定的理论指导。

1 圆形巷道围岩弹塑性分析

1.1 圆形巷道围岩应力分析

在地下工程如巷道等长洞型问题中，由于巷道轴向方向的尺寸远大于其横截断面尺寸，故可将该类工程问题视为广义平面应变问题[17]。广义平面应变问题是将巷道周围的应力场简化为平面应变、面外剪切以及单轴压缩的问题，简化模型示意图如图1所示，郑雨天等[17]通过上述模型推导出极坐标下巷道周边任意一点的应力表达式为

图1 广义平面应变问题模型Fig.1 Generalized plane strain problem model

式中：σr、σθ、τrθ分别为巷道周边任意一点的径向应力、切向应力以及剪应力；σx为垂直巷道帮部的水平应力；σy为与巷道轴向平行的应力；σz为巷道围岩的铅垂应力；σv为巷道轴向的应力；r、θ为巷道周边任意一点的极坐标；v为巷道围岩泊松比；R为巷道围岩半径。

极坐标下围岩任意一点的主应力表达式为

式中：σ1、σ2、与σ3为围岩任意点的三个主应力，式中的σ1、σ3并非一定是围岩的最大、最小主应力。

1.2 三向应力场下巷道塑性区边界方程

在研究巷道围岩的屈服与破坏时，需要建立使围岩产生屈服与破坏的条件与准则。M-C 强度准则是目前应用最为广泛的强度准则，其物理意义在于当剪切面上的剪应力与正应力之比达到最大时，材料便会发生屈服与破坏。M-C 强度准则在主应力空间的表述为

式中：C和φ分别为为屈服或破坏参数，即岩石的黏聚力和内摩擦角。

文献[5]将极坐标下任意一点的主应力σ1、σ3的表达式代入式(3)推导出平面应变问题下非均匀应力场中的塑性区八次隐性方程式(4)，并基于式(4)对巷道围岩塑性区形态进行深入研究，首次提出“蝶形塑性区”的概念，揭示了圆形巷道非对称变形破坏的机理。

其中：η为最大围压与最小围压的比值。从式(4)可以看出，蝶形塑性区八次隐性方程是将平面应变问题模型下的两向围压定义为最大（最小）、最小（最大）主应力，而未考虑巷道轴向应力σy的情况。事实上，圆孔围岩处于三向应力场下，在X、Y、Z三个方向的应力数值大小未知的情况下，无法判断哪个坐标方向的应力为最大主应力和最小主应力。

根据岩土塑性力学可知，3 个方向应力σx、σy、σz可以通过应力不变量与Lode 角表示为式(5)：

将极坐标下任意一点的应力表达式式(1)代入主应力表达式式(2)，得到的结果再分别代入偏应力第二不变量J2、偏应力第三不变量J3、应力Lode 角θσ以及平均应力σm各自的表达式，即可得各自的计算解析式，再将得到的计算解析式代入式(6)，即可得考虑轴向应力的三维应力场下的圆形巷道围岩塑性区边界隐性方程(7)：

由于该隐性方程的求解极其复杂，因此无法直接转换成塑性区边界解析式。可在三向应力σx、σy、σz以及巷道半径R、泊松比v、围岩黏聚力C和内摩擦角φ都给定的情况下，通过数学软件Maple 即可计算出巷道围岩的塑性区尺寸。

2 巷道塑性区尺寸及分布形态分析

在一般的地质围岩环境中，巷道所受围压比值为1～2，而在大埋深复杂地质构造带、高构造应力以及叠合采动应力影响下，巷道围压比值表现为非常规性，最大围压比值可高达10 倍以上。为研究不同应力场下圆孔的围岩塑性区尺寸及形态，此处设定水平侧压η1与轴向侧压η2分别为式(8)和式(9)，且由于篇幅有限仅研究深埋煤层条件，取巷道埋深为800 m 的应力环境，σz=20 MPa，黏聚力C=2 MPa，内摩擦角φ=30°，泊松比v=0.25，巷道半径为2 m。由于σx变化后的塑性区尺寸及形态与σz变化后旋转90°结果完全一致，因此仅讨论σx、σy的变化对孔洞围岩塑性区尺寸及形态特征的影响。

2.1 水平侧压对巷道塑性区尺寸及形态影响

为探究水平侧压η1对巷道塑性区尺寸及形态的影响，此处固定轴向应力σy=10 MPa，即固定轴向侧压将水平侧压η1从0.3 增加至1.8时对应的应力代入计算式(7)，得到不同η1情况下巷道帮部(坐标系0°)、翼角(45°)、顶底板(90°)处的塑性区尺寸，如图2 所示。

图2 不同η1 情况下巷道不同位置塑性区深度及分区Fig.2 Size and partition of plastic zone in different position of roadway under different η1

分析图2 可知：对于巷道顶底板而言，侧压系数η1在区间[0.3,1.3]时，塑性区变化范围较小，塑性区尺寸仅增加0.69 m，说明σx的增加引起的曲线斜率变化较小，称该区域为应力迟钝区。在该区域内，η1为0.4 时，顶底板不产生塑性区；η1在区间[1.3,1.8]时，塑性区变化范围较大，变化曲线呈指数型增长，塑性区尺寸增加2.83 m，最大塑性区尺寸达3.54 m。

对于巷道翼角而言，η1在区间[0.3,0.7]内处于应力敏感区，该区域内塑性区尺寸减少3.89 m；η1在区间[0.7,1.3]内处于应力迟钝区，该区域内塑性区尺寸变化仅0.03 m，η1=0.9 时翼角尺寸达到整个区域最小值0.07 m；η1在区间[1.3,1.8]内处于应力敏感区，塑性区范围增加5.90 m，最大塑性区尺寸达6.58 m。

对于巷道两帮而言，塑性区尺寸对η1的变化敏感性较差，在区间[0.3,1.8]内，塑性区仅变化0.56 m，η1为1.8 时，塑性区尺寸达最大值1.17 m。

由式（7）可以看出，该隐式方程的求解在实际应用时较为困难。为使巷道围岩塑性区计算变得简单、快捷，采用Python 开发了“巷道围岩塑性区求解软件”系统，系统界面如图3 所示。

图3 巷道围岩塑性区求解软件操作界面Fig.3 Software operation interface for solving plastic zone of roadway surrounding rock

基于已开发的塑性区求解软件，选取侧压系数η1为0.3、0.5、0.8、1.0、1.2、1.5 及1.8 共7 种情况，将对应的应力代入式(7)得不同水平侧压下的巷道塑性区形态如图4、5 所示。

图4 η1≤1 时围岩塑性区形态演化规律Fig.4 Evolution law of plastic zone morphology of surrounding rock when η1 ≤ 1

由图4 可以看出，当η1=0.3 时，巷道塑性区轮廓呈四象限突出，坐标轴处凹陷的蝶形形态，最大塑性区尺寸发生在象限角平分线附近；当η1增加至0.8 时，巷道塑性区最大塑性区半径发生在横轴，最小塑性区半径发生在纵轴，塑性区形态呈横椭圆形态；当η1为1 时，圆孔各处塑性区半径一致，呈标准的圆形形态。

由图5 可知，当η1为1.2 时，巷道最大塑性区半径在坐标纵轴，最小塑性区半径在坐标横轴，呈竖椭圆形态；随着η1的继续增大，最大塑性区半径开始由纵轴向纵轴两侧扩展，η1为1.5 时，塑性区形态呈类蝶形形态；当η1为1.8 时，最大塑性区半径发生在角平分线附近，塑性区形态呈蝶形形态。

图5 η1＞1 时围岩塑性区形态演化规律Fig.5 Evolution law of plastic zone morphology of surrounding rock when η1＞1

从上述分析可以看出：

1）固定轴向侧压η2的情况下，变化水平侧压η1时围岩顶底板及翼角处破坏会分区域出现应力敏感区和迟钝区，而围岩两帮的塑性区尺寸对η1变化的敏感程度较小。

2）在η1从0.3 增大至1.8 的过程中，巷道塑性区形态会呈现蝶形→椭圆→圆形→椭圆→蝶形3 种形态的演化过程。

2.2 轴向侧压对巷道塑性区尺寸及形态影响

为探究轴向侧压η2对巷道围岩塑性区尺寸及形态的影响，取水平侧压η1为1、1.2、2 三种情况，对相同η1不同轴向侧压η2情况下的巷道塑性区尺寸及形态进行分析，具体分析方案详见表1 所示。需要说明的是，在方案三中，η2取0.3、0.4、0.5 时，围岩产生的高偏应力过大，根据式(7)知，巷道周围已经产生完全破坏，因此不对该3 种情况进行讨论。

将方案一中的σx、σz代入平面应变问题下的塑性区边界方程式(4)，得到不同轴向侧压条件下巷道顶底板、帮部、翼角处塑性区尺寸如图5 中红色线条所示，由于式(4)不考虑巷道轴向σy的影响，因此相同σx、σz情况下，变化η2时巷道不同位置的塑性区尺寸均不会发生变化，因此红色线条恒为直线。将方案一中不同η2下的三向应力代入式(7)，得到不同轴向侧压η2情况下的塑性区尺寸，如图6 中紫色线条所示。

图6 当η1=1 时不同η2 情况下巷道不同位置塑性区尺寸及分区Fig.6 Size and partition of plastic zone in different position of roadway under different η2 when η1=1

由图6 可知：①η1=1 时，圆形孔洞顶底板、两帮以及翼角处的围岩塑性区尺寸随η2的增加变化趋势及数值完全一致，说明η1确定的情况下，η2的变化会使围岩各个方向的塑性区等量增长。②在区间0.5～1.5，两种方程计算下的塑性区尺寸均为0.61 m，说明该区域内σy的变化对圆孔的塑性区尺寸没有影响，笔者将该区域定义为轴向应力无影响区。在区间0.3～0.5 以及1.5～3.0 范围内，两种方程计算下的塑性区尺寸存在差异，笔者将该区域定义为轴向应力影响区。③在区间0.3～0.5 内，塑性区尺寸呈负指数型下降，说明该区域塑性区尺寸对σy的变化十分敏感，最大塑性区尺寸达2.03 m；在区间1.5～3.0 内，变化曲线呈指数型增长，最大塑性区尺寸达3.89 m。

方案二中不同轴向侧压η2条件下的塑性区尺寸，如图7 所示。由图7 可知：①η1=1.2 时，随着η2的增加，圆形巷道顶底板、两帮以及翼角处的围岩塑性区尺寸的变化趋势均呈现强烈的区间效应。在区间0.3～0.5 内均为轴向应力影响区，塑性区尺寸曲线呈负指数型下降，最大塑性区尺寸分别为6.39、2.67、4.95 m。②圆孔顶底板、两帮以及翼角处的轴向应力无影响区间分别为0.5～1.8、0.5～1.6、0.5～1.7，该区间内塑性区尺寸分别恒定为0.68、0.57、0.65 m。③巷道顶底板、两帮以及翼角处的第二次轴向应力影响区间分别为1.8～3.0、1.6～3.0、1.7～3.0，在该区间内塑性区尺寸曲线斜率急剧增加，当η2=3 时，最大塑性区尺寸分别达3.19、2.21、3.00 m。

图7 当η1=1.2 时不同η2 情况下巷道不同位置塑性区尺寸及分区Fig.7 Size and partition of plastic zone at different positions of roadway with different η2 when η1=1.2

方案三中不同轴向侧压η2条件下的塑性区尺寸，如图8 所示。由图8 可知：①η1=2.0 时，巷道的顶底板、两帮以及翼角在η2的变化下均呈现强烈的区间效应。在区间0.6～0.7 内均为轴向应力影响区，该区域内最大塑性区尺寸分别为1.58、0.79、3.33 m。②巷道顶底板、两帮以及翼角处的轴向应力无影响区分别为0.7～2.8、0.7～1.6、0.7～2.3，该区间内塑性区尺寸恒为0.91、0.44、1.45 m。③巷道顶底板、两帮以及翼角处的第二次轴向应力影响区间分别为2.8～3.0、1.6～3.0、2.3～3.0，该区间内塑性区随η2的增加而不断增加，η2=3 时的最大塑性区尺寸分别为1.12、1.12、4.00 m。

图8 当η1=2 时不同η2 情况下巷道不同位置塑性区尺寸及分区Fig.8 Size and partition of plastic zone at different positions of roadway with different η2 when η1=2

在方案一和方案二中，选取轴向侧压η2为0.3、1.5、3.0，在方案三中，选取η2为0.6、1.5、3.0，将3 种方案下η1、η2所对应的应力代入式(7)，得到不同侧压系数条件下的巷道塑性区形态如图9 所示。

图9 三种不同方案下塑性区形态演化规律Fig.9 Morphological evolution of plastic zone under three different schemes

由图9 可知，在固定η1=1 变化η2情况下，巷道围岩塑性区形态均为圆形形态，η2值的增加仅仅带来塑性区尺寸的改变，而无形态的改变。同样，当η1=1.2 变化η2情况下，巷道围岩塑性区形态为类“竖椭圆”形态。当η1=2 变化η2情况下，孔洞围岩的塑性区形态均为蝶形形态。

从上述3 种方案分析可以得到如下规律：

固定σx、σz变化轴向应力σy的过程中，巷道顶底板、两帮、翼角处的塑性区均随着η2的增加呈现强烈的区间效应，都会伴随η2的增加呈现轴向应力影响区、轴向应力无影响区、轴向应力影响区3 种区间效应。在轴向应力影响区间内，轴向侧压的增加或减少对围岩的塑性区尺寸影响都会很大。

结合2.1 的分析结果来看，巷道围岩的塑性区形态由水平侧压η1决定，轴向侧压η2对巷道围岩的塑性区形态影响较小，对尺寸影响较大。

2.3 数值模拟分析

为进一步说明上述数学手段分析结果的合理性，采用有限差分软件FLAC3D7.0 进行数值模拟分析。本文建立X轴、Y轴、Z轴长度分别为40、0.8、40 m的块体模型，采用放射状网格划分方式共生成单元格101 600 个，模型六面均采用位移约束，运算时间设置为自动求解，不平衡率达到10-5时运算停止。本构模型采用Mohr-Coulomb，具体岩层力学参数与上文数学分析采用的参数完全一致。

由于篇幅有限，仅对上文中2.1 节与2.2 节的方案三进行模拟结果分析。数学分析与数值模拟的塑性区形态对比如图10 所示。通过数学分析与数值模拟的塑性区特征对比图发现，2 种分析手段下的塑性区形态能够较好的吻合，在不同的水平侧压及轴向侧压条件下，巷道围岩塑性区的形态演化规律几乎完全一致，均呈现圆形、椭圆形与蝶形3 种形态。计算顶底板、翼角及两帮的数据，与上文数学分析所得的数据对比图如图11a、图11b所示。

图10 数学分析与数值模拟塑性区形态对比分析Fig.10 Mathematical analysis and numerical simulation of plastic zone morphology comparative analysis

图11 数学分析与数值模拟塑性区尺寸对比分析Fig.11 Mathematical analysis and numerical simulation of plastic zone size comparative analysis

为了得出数学与数值分析下不同位置塑性区尺寸变化的相关性，通过对比数学与数值模拟下不同位置的塑性区尺寸，采用拟合度R2指标来衡量2 种分析手段的相关程度。

由图11 可知，固定轴向侧压变化水平侧压的情况下，巷道两帮、翼角及顶底板的拟合度R2分别为0.97、0.93、0.90；固定水平侧压变化轴向侧压的情况下，巷道两帮、翼角及顶底板的拟合度R2分别为0.94、0.99、0.74。由相关性结果可以得出，6 组数据中前5 组数据的拟合程度都在0.9 之上，说明巷道顶底板、两帮、翼角位置，数学分析与数值模拟分析所得数据变化趋势基本一致。最后一组数据顶底板的相关性较低是由于数值模拟塑性区的计算取决于单元格大小，当两种η值所造成的破坏范围差值小于单位单元格时，数值模拟默认破坏范围一致，即数值模拟的网格依赖性问题，因此会出现部分η增加而斜率不变的情况。

综合图10 和图11 中数值模拟与理论分析形态及尺寸结果对比来看，当巷道围岩塑性区形态为圆形或椭圆形时，数值模拟与理论分析所得塑性区尺寸差值较小；当巷道为蝶形塑性区形态时，2 种计算结果的差值较大。这是由于数值模拟考虑了高偏应力场下应力动态调整过程中塑性区会进一步扩大的问题，而数学分析未能考虑该因素[19]。由此可以认为，在工程实践中，类似应力场条件下巷道围岩可能产生更大的破坏。

综上分析可知，数学分析与数值模拟分析在塑性区尺寸变化趋势及形态演化规律上吻合程度较高，更进一步证明了数学算法的准确性。

3 巷道围岩塑性区稳定性因素分析

从式(7)可以看出，巷道围岩塑性区尺寸除了会受到三向应力环境的影响之外，还会不同程度地受围岩黏聚力C、内摩擦角φ、巷道半径R以及泊松比v这几个因素的影响，因此本节在上述已讨论围岩应力对围岩稳定性影响的基础上，分析C、φ、R、μ四个参数对巷道围岩稳定性的影响规律。

3.1 黏聚力C 对巷道围岩稳定性的影响

为分析黏聚力C对巷道围岩稳定性的影响，设定σx=40 MPa，σy=12 MPa，σz=20 MPa，φ=30°，v=0.25，R=2 m，分别将C为1.5,2.0,2.5,3.0,3.5,4.0,4.5,5.0 MPa 代入式(7)，得不同黏聚力时的围岩顶底板、翼角、两帮塑性区尺寸以及塑性区形态，如图12所示。

图12 黏聚力对巷道围岩稳定性影响分析Fig.12 Analysis of the influence of cohesion on the stability of roadway surrounding rock

从图12 左侧点线图可以看出，巷道顶底板、翼角以及两帮的围岩塑性区尺寸均与黏聚力呈负相关，而3 个位置的变化速率却各不相同，随着黏聚力的增加，顶底板塑性区尺寸的降幅分别为5.62%，5.66%，5.92%，6.29%，1.95%，2.16%，2.52%，翼角处的塑性区尺寸降幅分别为35.76%，21.19%，15.63%，12.03%，2.96%，2.82%，2.69%，两帮的塑性区尺寸降幅分别为20.05%，10.97%，7.60%，5.55%，1.30%，1.24%，1.18%。由降幅可以看出，巷道3 个位置对黏聚力变化的敏感性有所差异，敏感性分别为翼角＞顶底板＞两帮。从极坐标图中可以看出，随着黏聚力的增加，塑性区蝶叶的退化速率逐渐减小，塑性区形态逐渐由“蝶形”向“蝶形前态”转变。因此，黏聚力较大时，巷道围岩的工程隐患下降，蝶形冒顶风险降低。

3.2 内摩擦角φ 对巷道围岩稳定性的影响

为分析内摩擦角φ对巷道围岩稳定性的影响，设定σx=40 MPa，σy=12 MPa，σz=20 MPa，C=2 MPa，v=0.25，R=2 m，分别将φ为29°,30°,31°,32°,33°,34°,35°,36°代入式(7)，得不同内摩擦角时的围岩顶底板、翼角、两帮塑性区尺寸以及塑性区形态如图13所示。

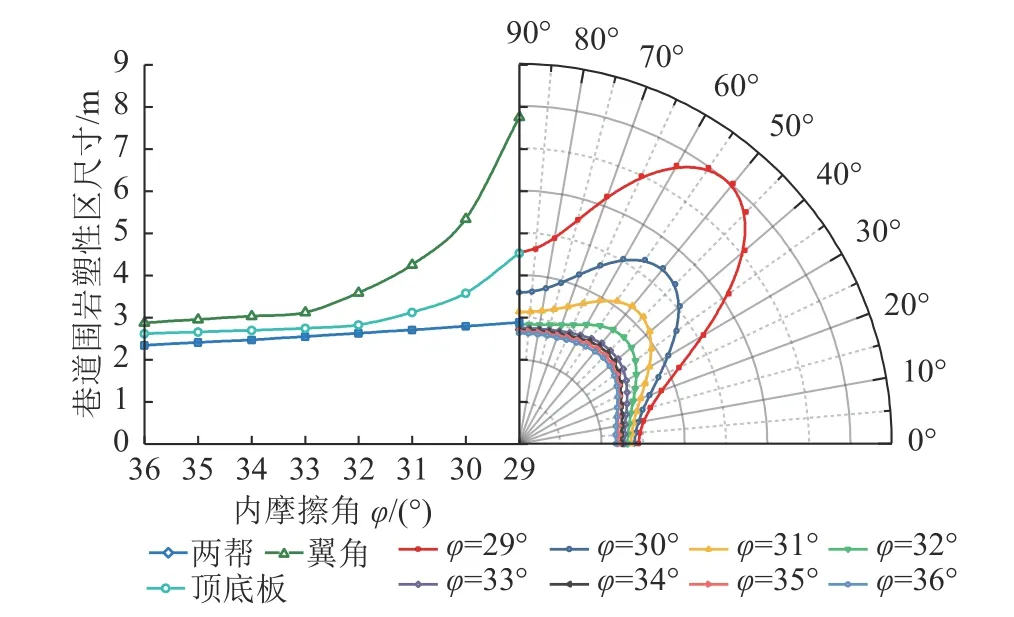
图13 内摩擦角对巷道围岩稳定性影响分析Fig.13 Analysis of the influence of internal friction angle on the stability of roadway surrounding rock

从图13 点线图分析可知，巷道顶底板、翼角以及两帮的围岩塑性区尺寸与内摩擦角呈反比关系。随着黏聚力的增加，3 个位置的围岩塑性区尺寸呈不同速率变化，顶底板的塑性区尺寸减小幅值为20.92%，12.82%，9.48%，2.90%，1.68%，1.58%，1.49%，翼角处的塑性区尺寸减小幅值为31.21%，20.27%，15.72%，12.86%，2.86%，2.70%，2.54%，两帮的塑性区尺寸减小幅值为3.23%，3.13%，3.04%，2.94%，2.85%，2.75%，2.65%。从减小幅值可以看出，随着内摩擦角的增大，3 个位置中翼角处敏感性最大，顶底板次之，两帮最小。且同一内摩擦角下，三者之间的塑性区尺寸始终为翼角＞顶底板＞两帮。从极坐标图中可以看出，内摩擦角较小时，蝶叶随着内摩擦角的增加退化速率较快，内摩擦角较大时，蝶叶退化速率逐渐减小。因此，内摩擦角越大，围岩的稳定性越好。

3.3 半径R 对巷道围岩稳定性的影响

为分析巷道半径R对巷道围岩稳定性的影响，设定σx=40 MPa，σy=12 MPa，σz=20 MPa，C=2 MPa，φ=30°，v=0.25，分别将R为2.0,2.5,3.0,3.5,4.0,4.5 m代入式(7)，得不同巷道半径时的围岩顶底板、翼角、两帮塑性区尺寸以及塑性区形态如图14 所示。

图14 巷道半径对巷道围岩稳定性影响分析Fig.14 Analysis of the influence of roadway radius on the stability of roadway surrounding rock

由图14 左侧点线图可以看出，巷道顶底板、翼角以及两帮的巷道围岩塑性区尺寸与巷道半径R呈正相关关系，且随着半径R 的增加，3 个位置处的敏感性大小排序为翼角＞顶底板＞两帮。顶底板、翼角处、两帮3 个位置处的围岩塑性区增幅均为25.00%，20.00%，16.67%，14.29%，12.50%。从极坐标图可以看出，随着半径R的增加，蝶叶塑性区形态呈均匀扩展。因此，巷道断面越大，围岩的塑性破坏越大，顶板发生冒顶的概率就越大。

3.4 泊松比v 对巷道围岩稳定性的影响

由2.2 节分析可知，σy对巷道围岩稳定性的影响区域可分为轴向应力影响区和轴向应力无影响区，在轴向应力无影响区内，围岩塑性区尺寸与平面应变下的蝶形破坏方程式(4)计算结果一致，由式(4)可知，泊松比v对巷道围岩的塑性区边界没有任何影响，由此可知，在轴向应力影响区域内，泊松比v不会对围岩的稳定性产生影响。

在轴向应力影响区内，为分析泊松比对巷道围岩稳定性的影响，设定σx=40 MPa，σy=12 MPa，σz=20 MPa，C=2 MPa，φ=30°，R=2 m，分别将v为0,0.1,0.2,0.3,0.4,0.5 代入式(7)，得不同巷道泊松比时的围岩顶底板、翼角、两帮塑性区尺寸以及塑性区形态如图15 所示。

图15 泊松比对巷道围岩稳定性影响分析Fig.15 Analysis of the influence of Poisson ' s ratio on the stability of roadway surrounding rock

由图15 左侧点线图分析可知，巷道顶底板、翼角以及两帮的巷道围岩塑性区尺寸受泊松比影响会呈现不同的变化趋势，随着泊松比的不断增加，顶底板的围岩塑性区尺寸呈先急剧减小后缓慢下降，在v=0.4 和0.5 时塑性区尺寸均为2.91 m，两帮的围岩塑性区尺寸在v=0、0.1、0.2 时保持一致，均为2.44 m，从v=0.2 开始塑性区尺寸不断增加，翼角处的塑性区尺寸不受泊松比的影响，塑性区值恒为5.33 m，是因为在式（1）中，当θ=45°时，余弦函数的值为0，轴向应力仅受σy值的影响。由极坐标图分析可知，随着泊松比的不断增加，围岩较小应力（σz）方向的塑性区尺寸不断减小，较大应力（σx）方向的塑性区尺寸逐渐增加。因此，当泊松比较小时，巷道冒顶的概率较大，要特别注重对巷道顶板及翼角处的支护。

综合文章的第2 章第3 部分的分析来看，侧压系数、黏聚力、内摩擦角、巷道设计半径、泊松比等因素对巷道围岩的稳定性不尽相同。当侧压系数较小时，围岩塑性区形态为圆形、椭圆形形态，侧压系数较大时围岩塑性区形态会呈现蝶形形态，即侧压系数为影响巷道围岩稳定性的先决条件。内摩擦角、黏聚力在合理参数范围内变化时，巷道最大塑性区尺寸先呈指数型变化而后转变为线性变化；巷道半径及泊松比在变化过程中最大破坏半径呈线性变化。黏聚力C、内摩擦角φ、泊松比v、巷道半径R为影响巷道围岩稳定性的主要条件。

4 对工程实践的指导

研究了轴向应力对巷道围岩稳定性的影响，当水平侧压及轴向侧压较大（较小）时，围岩的塑性破坏范围较大。研究可从以下2 个方面指导工程实践。

4.1 巷道取向判据

在深部开采条件下，巷道布置的方向对围岩的变形破坏具有很大影响，甚至在一定程度上超过支护本身造成的影响[20]。因此要依靠正确调整巷道方向与应力场方向的关系，削减构造应力对围岩稳定的影响。

当巷道旋转一定角度后受力分析如图16 所示。假设巷道沿Y轴布置，巷道初始轴向与σy平行，α为巷道旋转角，即σy与巷道轴向的夹角为垂直巷道帮部的应力为平行巷道轴向的应力。

图16 巷道轴向旋转α 角度后受力分析Fig.16 Stress analysis chart of roadway after axial rotation α angle

因此在巷道掘进前，可根据地应力测试结果，依据三向应力塑性区方程确定较优的巷道布置方向，避免巷道布置在蝶形应力环境区域。

4.2 巷道灾害预测及治理

可依据理论公式判断某种三向应力环境下的围岩塑性区形态，若围岩的塑性破坏产生蝶形塑性区，要对蝶叶扩展部位进行加强支护。此外当巷道不可避免的布置在高偏应力环境时，要通过工程手段如高应力方向卸荷等来改善围岩的应力环境。

5 结论

1）在相同轴向侧压不同水平侧压条件下，巷道围岩塑性区尺寸变化分为迟钝区和敏感区，且不同水平侧压下围岩的塑性破坏会呈现圆形、椭圆形及蝶形3 种形态。

2）在相同水平侧压不同轴向侧压条件下，围岩的塑性区尺寸变化呈现强烈的区间效应，基于平面应变求解下的塑性区尺寸将影响区间分为轴向应力影响区和轴向应力无影响区，在轴向应力影响区内，轴向侧压随围岩的塑性区尺寸影响很大，充分说明了轴向应力的重要性。

3）水平侧压对围岩塑性破坏的尺寸影响较大，轴向侧压对塑性破坏的形态几乎无影响，对塑性区尺寸影响较大。

4）巷道围岩的黏聚力、内摩擦角越大，围岩各个位置的塑性区尺寸越小，冒顶风险越低。围岩的塑性区尺寸会随着巷道半径的增加呈等差数列增长。在轴向应力无影响区内，巷道围岩的塑性区尺寸不会受到泊松比的影响，在轴向应力影响区内，翼角处的塑性区尺寸恒为定值，随着泊松比的增加，围岩塑性破坏向围压较大一侧方向扩展。