基于撞击流调控的煤泥水混合过程强化研究
唐海龙,樊玉萍,马晓敏,董宪姝,常 明
(1.太原理工大学 矿业工程学院,山西 太原 030024;2.太原理工大学 山西省生态矿业工程研究中心,山西 太原 030024)
0 引言
湿法选煤是煤炭清洁高效利用的重要途经,我国每年因洗选产生的煤炭废水高达几十亿立方米,这些废水通常采用浓缩压滤方式净化回用[1-2]。为使平行处理的各浓缩机入料浓度及颗粒粒度、密度等性质保持一致,需要混料桶对样品进行充分混合后分配至各浓缩机中。煤泥水混料桶虽结构简单,但内部流场复杂,且对入料前添加凝聚剂的凝聚效果及后续浓缩机的絮凝效果有着重要作用[3]。混料桶内部为强紊流混合区。强紊流混合区产生局部强剪切,增大颗粒、药剂间的速度差异,强化药剂在颗粒表面的碰撞吸附[4]。所以针对混料桶流场特性和颗粒运动行为进行研究,对于优化混料桶结构和提升生产效率有实际意义。
流体中普遍存在着颗粒碰撞行为[5]。对于混料桶内部流场,流体输运的湍流效应和颗粒运动的碰撞相互影响[6]。湍流在物理结构上可以看作是不同尺度涡旋叠加组合形成的流动,这些涡的尺度大小以及旋转轴的方向是随机分布的。大尺度涡的尺寸近乎流场的大小,其主要决定条件是流场的边界条件,大尺度涡是导致低频脉动的主要原因;大尺度涡持续破裂导致涡尺度不断减小,直至产生最小尺度涡,小尺度涡的尺寸约为流场尺度的1/1 000 量级,其主要决定条件是流体的黏性力,小尺度涡是导致高频脉动的主要原因[7-10]。流体流动是否产生涡旋对颗粒的运动状态有着非常大的影响,要合理利用涡旋,就需要对其本质机理有明确认识,从而充分利用其优势,促进颗粒碰撞[11]。而撞击流反应流场中存在着大量无序的湍流涡结构,使其具有良好的混合效果[12-13]。研究显示,造成水中微细颗粒之间的碰撞的本质原因是湍流的亚微观结构,也就是在湍流过程中所形成的微涡旋[14]。微涡旋流动可以很好的增进流体里微细颗粒的扩散与接触,主要有以下两点原因[15]:①涡流形成的流层之间存在的速度差异导致的流体相对运动造成其中的微粒发生相对运动[16];②涡流的旋转特性,旋转的流体夹带的微粒由于离心力在涡旋中做径向运动,从而促进了微粒间的碰撞。当微涡旋尺度越接近颗粒尺度时对颗粒间相互碰撞越有利[17-18]。湍流中,颗粒有效碰撞次数为碰撞频率与时间的乘积,所以设备中的搅拌强度和搅拌时间对水中颗粒的碰撞有重要影响[19]。
通常整个流场以及单个颗粒和群体颗粒的动力学问题通过采用数值模拟的方式进行量化分析[20-21]。模拟中,组分输运模型(Species Transport) 和DPM(Discrete Phase Model)模型相互结合可有效仿真有化学反应混合[22]和无化学反应混合过程[23]。同比例改变混料桶体积大小对内部流场影响较大,因而在实验室进行试验较为困难,立足于开发煤泥水液-液混合,液-固分离过程强化处理设备,采用数值模拟研究了装置内部混合流体运动规律,分析了颗粒分布规律,为混合凝聚装置水力参数优化提供了理论依据和数据支撑[24]。
1 模拟方案
1.1 结构及网格划分
此次数值模拟混料桶模型为塔山煤矿选煤厂煤泥水混料桶,其结构如图1a、1b 所示,桶体段高度为2 000 mm,内径为1 800 mm,入料口及出料口位置如图1c、1d 所示。上入料口(进料口1)的直径为625 mm,侧入料口(进料口2 和进料口3)的直径均为525 mm,且进料口1、2、3 的入料角度两两垂直。出料口的直径为725 mm。文中将侧入料口以下区域称为桶体下部区域,侧入料口以上区域称为桶体上部区域。
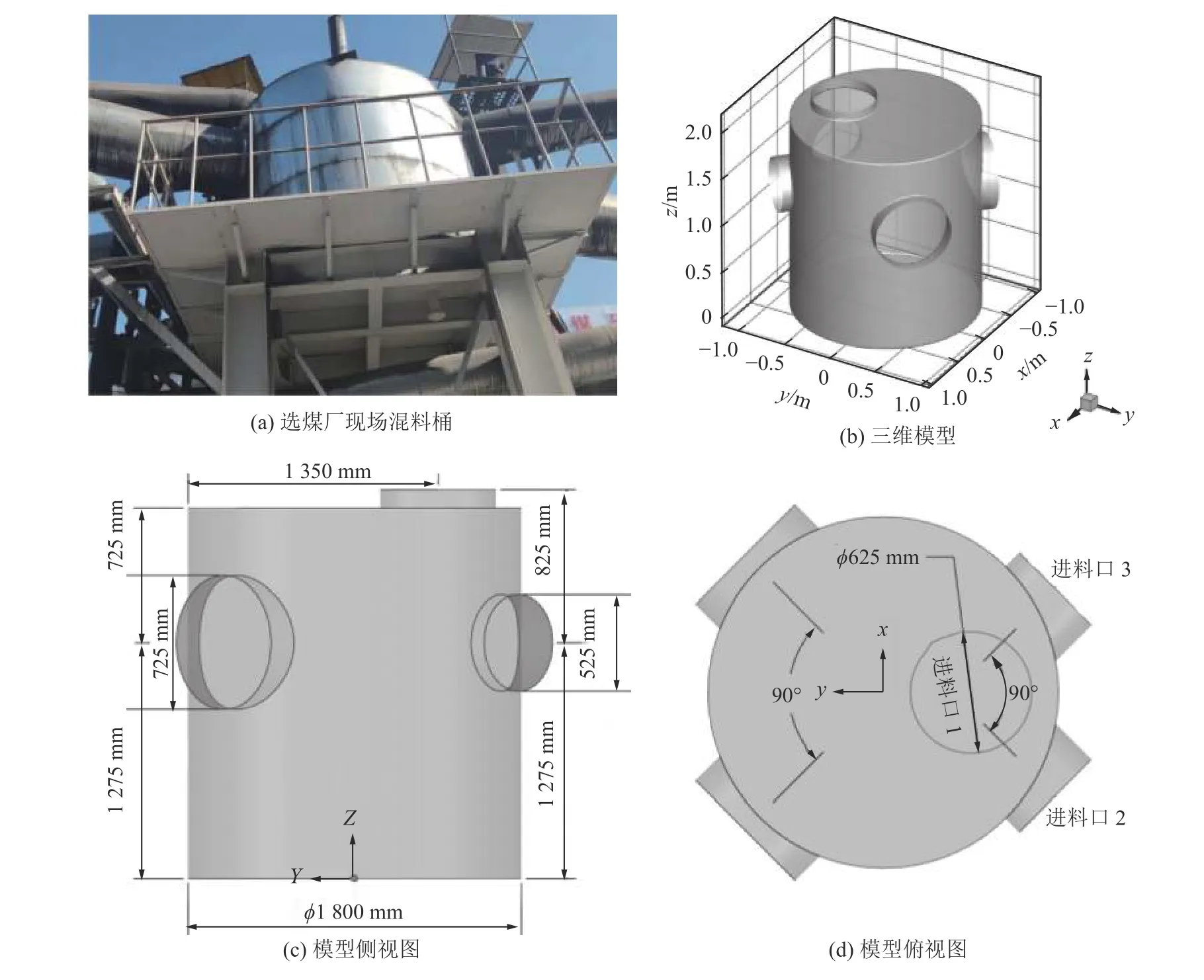
图1 混料桶尺寸结构Fig.1 Dimensional structure of the mixing drum
由上入料口和侧入料口进入的悬浮液射流相互垂直交叉碰撞,形成射流-撞击流。相互碰撞的流体会向周边扩散,扩散较快的区域和扩散较慢的区域之间会形成压力差。流体向着低压区快速移动形成涡流区域,从而达到搅拌混合的目的。在搅拌混合时可加速细微颗粒扩散和运动,产生的涡旋能有效增大颗粒碰撞概率,在混料桶加入凝聚剂可增强凝聚效果。由于凝聚剂对桶体内流场的影响极小,所以此次模拟没有考虑凝聚剂,只考虑涡的演化及颗粒运动。
此次模拟采用Fluent Meshing 软件进行非结构化网格划分,选择六面体/多面体混合网格,如图2 所示。内流场区域采用六面体网格划分,边界层采用多面体网格划分。数值模拟前进行了网格无关性检验,如图3,当网格数量达到148 万时,体积平均湍动能耗散率趋于稳定。综合计算准确性及成本,最终选取网格总数约 148 万的划分策略。

图2 网格划分Fig.2 Grid division

图3 网格无关性检验Fig.3 Grid independence verification
1.2 流体参数选择
对混料桶模型采用组分输运模型进行不同流速比条件混料桶的流场数值模拟,采用DPM 模型进行流场-颗粒双向耦合模拟。
模拟前测定了煤泥水悬浮液密度和黏度随固体颗粒的密度、粒度及浓度的影响规律(温度为16 ℃,选用NDJ-9S 旋转黏度计)结果如图4、5 所示,组分输送模型采用为不同密度物料在不同vup(上入料口的入料流速)和vside(侧入料口的入料流速)下混料桶内部流场变化,模拟入料性质参照选煤厂浓缩旋流器溢流和快开压滤机滤液,其密度分别为1 237 kg/m3和1 025 kg/m3。DPM 模型探究了如表1 所示的4种颗粒在混料桶流场中的分布状态和运动轨迹,受计算能力限制,DPM 模型中对10-6s 内产生的颗粒进行定位跟踪,此次模拟中形成了3 620 个pacel(DPM模型中将一定数量颗粒打包为一个pacel,颗粒和流场之间的相互作用是以pacel 为单位进行的),总共形成颗粒数为4 958 个,每个pacel 包含1.369 6 个颗粒。

表1 DPM 模型固体颗粒参数Table 1 DPM model solid particle parameters

图4 悬浮液密度随颗粒密度及浓度变化Fig.4 Variation of suspension density with particle density and concentration

图5 悬浮液黏度随颗粒粒度及浓度变化Fig.5 Variation of suspension viscosity with particle size and concentration
1.3 数学模型
考虑到煤泥水中固体颗粒粒度较细(大多小于500 μm),且研究采用高浓度、较大粒度和低浓度、较低粒度煤泥水混合,因此数值模拟设计为高浓度组分和低浓度组分两组分混合输送模型处理两种不同密度和黏度流体流动,组分输送模型选用 realizekε模型计算湍流,主要控制方程如下:
式中:Ds为组分S在水体中的扩散系数;Cs为该组分的体积浓度;ρCs为 该组分的质量浓度;Ss为该组分的生产率。
利用时间平均的三维瞬态 Navier-Stokes 方程、能量方程和连续性方程,采用有限体积法,将欧拉框架内的液体流动作为连续相求解。在物质输运模型中,笔者在 Eulerian 参考系中求解了另一个非反应性的两物质输运方程(不同密度、黏度的液体),以确定煤泥水的质量分数。在离散相模型中,采用拉格朗日框架下 Fluent 的粒子跟踪法(离散相模型)在连续相(水)内跟踪颗粒。
作用在颗粒上的重要力是阻力、升力和重力(浮力)。通过将拉格朗日坐标系下的粒子力平衡方程沿i方向积分,确定了液相中粒子的运动轨迹。
DPM 模型控制方程:
其中,ui为 流体相速度为粒子速度;ρ为流体密度,ρp为颗粒密度是单位粒子质量的阻力,由 Stokes-Cunningham 阻力定律给出,Cc=1+2λ/dp[1.257+0.4e-(1.1dp/2λ)]是亚微米颗粒的 Cunningham 修正因子。λ=6.6×10-8是分子的平均自由路径。等式右边的第二项是重力,最后一项Fi包括作用在粒子上的所有附加力,即升力、虚拟质量力、布朗力和压力梯度力。利用Saffman 升力方程建立了升力模型。
1.4 边界条件
入料口均设置为速度入口(Velocity Inlet),入料口流速设置见表2,出料口均设置为压力出口(Pressure Outlet),静压设置为 0(表压),固体壁面为无滑移壁面,借助 ANSYS FLUENT 软件进行求解,采用隐式求解器算法对控制方程进行离散化处理,多组分输送模型采用 SIMPLE 算法进行压力-速度耦合计算,密度混合法则采用容积比重混合法则,黏度混合法则采用质量加权混合法则,方程离散格式中,梯度采用 Least Squares Cell Based 格式,动量项和质量分数,湍流动能项、湍流耗散率项均采用二阶迎风格式;DPM 模型工作介质使用室温下的水,并添加1.3节中提到的附加力。收敛残差精度设置为 10-4,计算采用非稳态求解,时间步长设置 10-4s,计算约36 s达到统计学稳定后,取后10 s 作时均处理用于后续结果分析。如无特别说明,后处理结果均取混合相的物理参量值。

表2 入料口入料流速方案Table 2 Feed flow rate scheme at the inlet
2 计算结果分析
2.1 湍流特征分析
湍流动能表征湍流流态下流体的速度脉动强度,决定微细颗粒是否能获得足够大的动能突破流线与较大颗粒发生碰撞,湍流耗散率表征由于速度梯度产生的流体内摩擦引发湍流动能耗散的速率,与湍流最小涡尺度密切相关,涡尺度与其能有效作用的颗粒尺寸相关。
1)涡产生机理。当vup∶vside为1.882∶1.258,且ρup(上入料口入料密度)和ρside(侧入料口入料密度)相同时轴向截面与展向截面上的流体压力分布如图6所示。图6a 为Z=200、700、1 250、1 800 mm 等各截面上压力及整体混料桶流线空间分布图,图中由于入料流向在桶体下部靠近出口一侧形成了高压区域,靠近入口一侧形成低压区域,由流线可以看出流体从高压区域流向低压区域。沿轴向,如图6b 为Y=0截面所示,相互正交流向的流体在经过桶体之后,在Y-Z面两侧形成了压力较低的负压区,该区域内沿流动方向压力递增,即出现了逆压梯度,流体回流,形成涡旋,其旋转流动的旋转轴垂直于轴向,为展向涡;从图6a 可以看出部分桶体下部区域的上升流体又进入了桶体上部区域的展向涡区域。同样,图6c 为Z=700 mm 截面所示的展向截面上,桶体900 mm 以下两侧的逆压梯度促使图中所示轴向涡的形成。结合图6a 和6c 可以得知在桶体下部区域Y-Z面两侧形成了螺旋上升的发卡涡。展向涡和轴向涡强化流体内细微颗粒团聚,发卡涡强化上-侧入料不同密度流体之间的混合。

图6 混料桶内压力云图Fig.6 Pressure cloud in the mixing drum
2)混料桶内宏观涡演化过程。采用Q准则识别叶轮生成的湍流涡结构。通常情况下流体区域中当Q>0 时认为有旋涡产生,即旋转部分的涡量大于变形部分[25],Q准则特征方程为
其中,Ω为速度梯度张量的反对称分量(旋转速率张量);S为速度梯度张量的对称分量(应变速率张量)。分别对应流场中的旋转与变形。图7 为不同入料流速比下Q=0.01 时涡三维等势面图,并用流体流动速度着色。分析可知,在进料流速比相同的情况下,ρside>ρup时桶体内所产生的涡的涡尺度明显大于ρup>ρside时所产生的涡的涡尺度。在进料密度相同情况下,vup∶vside为1.882∶1.258 时,桶体下部宏观涡尺度最小,桶体上部展向涡尺度最大。当vup:vside为1.258∶1.258 和1.882∶1.870 时涡形态基本相同,在ρup>ρside情况下,桶体下部发卡涡尺度减小,涡通量增大,涡强度增强,小尺度涡更有利于流体混合。
对于涡等势面上速度分布,在流体交叉碰撞区至出料口区域速度较高,而桶体上部及桶体下部远离入料口区域以及宏观涡区域速度较低,由此形成了速度梯度区,涡流中不同流层间的速度梯度及桶内区域之间的剪切速率可有效强化流体间相互混合及颗粒间相互碰撞。
3)湍流动能。混料桶X=0 mm、Z=200 mm、400 mm、700 mm、1 000 mm、1 200 mm、1 500 mm、1 700 mm各截面上不同入料流速比下的湍流动能三维空间分布如图8 所示。流体进入桶体时,各流速比下湍流动能均有增大趋势,桶体下部靠近侧入料口区域和桶体上部远离上入料口区域湍流动能低于其他区域,随着与撞击点距离的增加,流体湍流动能不断衰减,可见垂直交叉流诱导出的一系列湍流涡及其相互作用增强了湍流脉动。此外,入料流速对湍流动能分布影响显著,结合图7 涡演化特性分析,在入料密度相同情况下,随着入料流速增加,高湍流动能区域增大,高湍流动能区中涡与涡之间的强相互作用对不同流体之间混合起强化作用。
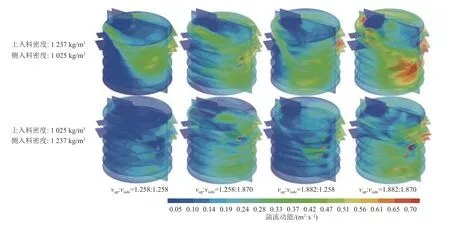
图8 不同入料流速比下混料桶内湍流动能空间分布云图Fig.8 Spatial distribution contours of turbulent kinetic energy in the mixing drum at different inlet fluid velocity ratios
4)最小涡尺度。湍流中,大尺度涡从主流体中不断获得能量,然后通过不同尺度涡之间和相同尺度涡之间的相互作用,能量逐渐传递至小尺寸涡中。最后因为流体粘性力持续作用导致能量耗散,小尺度涡逐渐消失,湍流流体中的能量转化为流体的内能[26]。根据Kolmogorov紊流微涡旋理论,最小涡尺度λ数学表征[27-28]为
式中:v为流体的运动黏度,m2/s;ε为单位质量水体耗散的有效能耗,m2/s。利用式(7)可计算桶体内各区域的最小涡尺度大小以及各部分最小涡尺度均值,如图9 所示。

图9 不同入料流速比下混料桶内最小涡尺度空间分布云图Fig.9 Spatial distribution contours of the minimum vortex scale in the mixing drum at different inlet fluid velocity ratios
根据图9,在混料桶各研究区域范围内,任意流速比均可诱导出μm 级小尺度涡,混料桶内靠近出料口一侧最小涡尺度小于靠近入料口一侧的最小涡尺度。结合图10,在实际流速比相同情况下,ρup>ρside时桶内产生的最小涡尺度均小于ρside> ρup时所产生的最小涡尺度,当上入料口和侧入料口入料流速均为1.258 时,两密度条件下桶内最小涡尺度平均值分别为96.83 μm 和104.99 μm,已达到颗粒有效碰撞涡尺度。vup∶vside从1.882∶1.258 降低至1.258∶1.870时,桶内产生的最小涡的尺寸在大多数区域呈现减小趋势,最小涡尺度平均值减小,最小涡尺度的减小对流体内能有效传递于细微颗粒有有利作用。在上-侧入料密度不变的条件下,当ρup>ρside时,随着vup∶vside增大,湍流动能和湍流耗散率缓慢增大,高湍流作用区域范围增大。当ρup<ρside时,湍流动能和湍流耗散率减小,高湍流作用区域范围减小。当流速比相近,仅流速增大时(vup∶vside从1.258∶1.258 增大至1.882∶1.870),湍流动能和湍流耗散率增大且湍流耗散率变化比湍流动能变化更快,流体内能量耗散速度加快,最小涡尺度减小。通过计算各流速比最小涡尺度最小值、平均值、最大值之间的差值可得知最小涡尺度主要以小于平均最小涡尺度的涡为主。
2.2 流体性质分析
根据流体混合原理,理论混合密度公式为加权平均:

表3 不同入料流速比下混料桶内理论混合密度Table 3 Theoretical mixing density in the mixing drum at different inlet fluid velocity ratios
湍流黏度(涡黏系数)和混合长度的平方同平均流速梯度的乘积成正比,湍流黏度的量纲中,可以知道湍流尺度的平方与时间成正比关系,其中,大尺度湍流是混合的促成因素[29]。湍流黏度反映的是流体作湍流运动时所产生的黏性应力和附加应力,其中附加应力包括法向附加应力和切向附加应力,这些附加应力都是湍流所特有的,是由于流体质点的脉动产生的。
上-侧入料口不同入料密度下不同流速比的情况中,理论混合密度在桶体中分布等值面如图11,并用等势面上得湍流黏度变化对其着色。由图可得,同一流速比时,理论混合密度等值面图在ρup>ρside时桶体内所占据尺度均大于ρup<ρside时的尺度。不论入料密度变化,当实际流速比为1.882∶1.258 时,理论混合密度等值面的表面积均达到最大。ρup>ρside时,沿Z 轴负方向湍流黏度逐渐增大;ρup<ρside时,沿Y轴正方向湍流黏度逐渐增大。流速比相同时理论混合密度等值面图上ρup>ρside时的湍流黏度均大于ρup<ρside时的湍流黏度,湍流黏度越大,流体速度梯度越大,湍流动能耗散越快,小尺度涡分布越密集,其更有利于流体混合及颗粒碰撞。

图11 不同入料流速比下混料桶内理论混合密度等值面Fig.11 Isosurfaces of theoretical mixing density in the mixing drum at different inlet fluid velocity ratios
根据图12 中湍流黏度随桶体高度的不同而变化的分布云图,当上-侧入料流速比小于1.0 时,在ρup>ρside的情况下,湍流黏度会随桶高位置的上升而呈现先增大后减小的趋势,在725~1 025 mm 内达到最大值;在ρup<ρside的情况下,湍流黏度会呈现随桶高位置的上升而逐渐减小的趋势,但在高度大于1 500 mm 的位置有一个明显增大。而当上-侧入料流速比大于1.0 时,两种不同入料密度情况下,湍流黏度会随桶高位置的上升均呈现出逐渐减小的趋势,说明在ρup>ρside情况下,增大上-侧流速比可增强桶体下部区域流体混合和对颗粒作用;在ρup<ρside的情况下,减小上-侧流速比可增强桶体下部区域流体混合和对颗粒作用。且不论入料密度如何变化,桶体下部的湍流强度均大于桶体上部,因而桶体下部区域体积大小对流体混合效果有较明显影响。
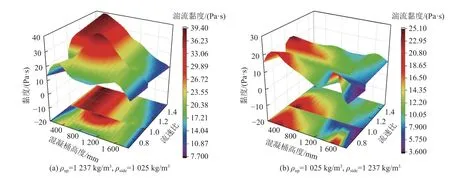
图12 不同流速比下湍流黏度随桶体高度变化Fig.12 Variation of turbulent viscosity with drum height for different velocity ratios
当ρup>ρside时,如图13a,流速比在0.67~1.05 和大于1.49 情况下,桶体内各等高平面平均密度随桶体高度上升而增大,且流速比在0.67~0.7、1.0~1.1、1.40~1.50 时桶内密度分布较为均匀。流速比在1.05~1.49 时,桶体内各等高平面平均密度随桶体高度上升而减小。流速比在0.67~1.05 时,在桶体高度1 150~1 750 mm 范围内密度有明显增大,而流速比在1.05~1.49 时,在桶体高度1 150~1 750 mm 范围内密度有明显减小,由于桶体高度1 150~1 750 mm是侧入料口和出料口的分布区域,所以流速比在0.67~1.05 时,在桶体高度1 150~1 750 mm 范围的密度受上入料口入料密度影响较大,流速比在1.05~1.49 时,在桶体高度1 150~1 750 mm 范围的密度受侧入料口入料密度影响较大。图13b 中,当ρup<ρside时,桶体高度在1 250 以下时桶体内各等高平面平均密度基本保持均匀,当桶体高度高于1 250 时,流速比在0.67~0.7、1.40~1.50 及接近1.10 时桶内密度分布较为均匀。流速比在0.70~1.10 间时流体密度明显降低,流速比在1.10~1.45 时流体密度明显增大。说明当ρup<ρside时,流速比小于1.10 的情况下,由侧入料口进入的流体主要进入桶体下部区域,而流速比大于1.10 的情况下,由侧入料口进入的流体流入桶体上部区域的较多。
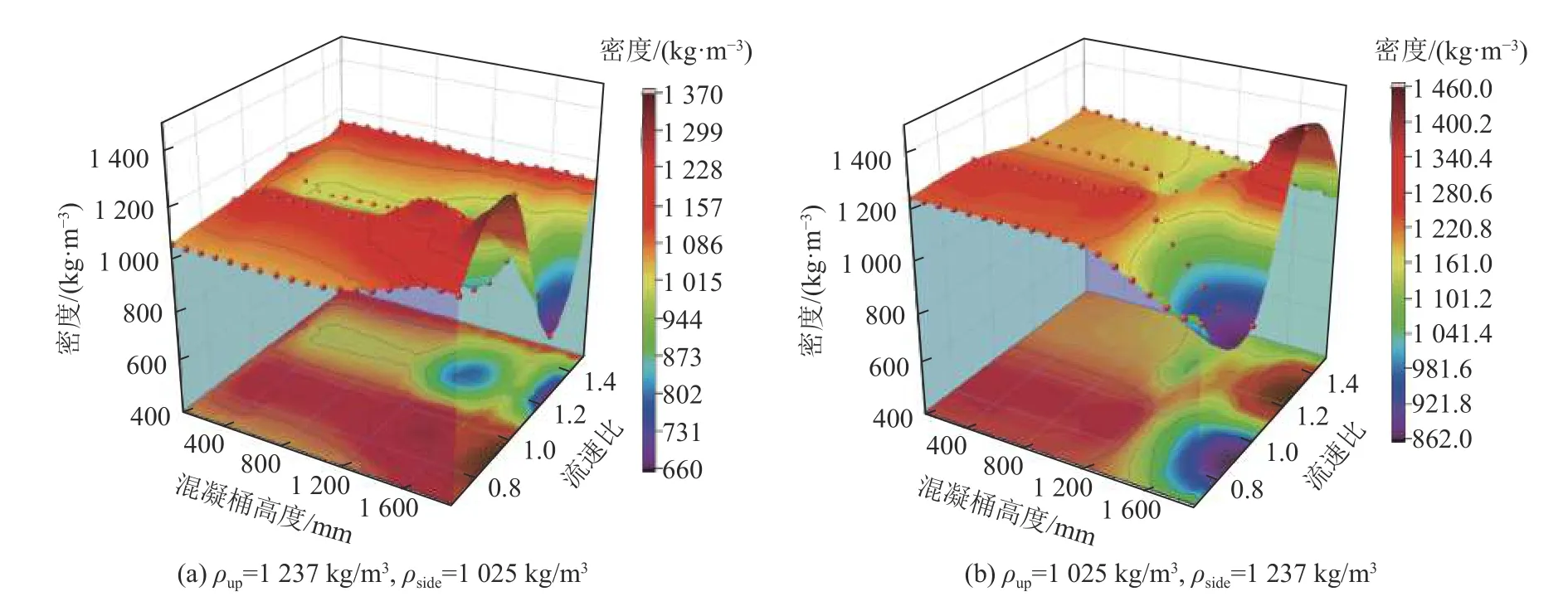
图13 不同流速比下流体密度随桶体高度变化Fig.13 Variation of fluid density with drum height for different velocity ratios
图14 中对不同等高面上不同流速比下混合流体表观黏度而言,其表观黏度和混合流体密度分布特征基本一致。表观黏度是在一定速度梯度下剪切应力和剪切速率的比值,在同一流速比下剪切速率变化较小,再结合图7,在ρup>ρside情况下,上-侧入料流速比小于1.05 时,桶体下部剪切应力较大;上-侧入料流速比在1.05~1.40 时,桶体下部剪切应力较小;上-侧流速比在1.4~1.5 时,桶体内表观黏度最为均匀,因而桶内流体剪切应力随桶高变化不大。在ρup<ρside情况下,上-侧入料流速比小于1.10 时,桶体上部流体剪切应力较小;上-侧入料流速比大于1.05 时,桶体上部剪切应力较大。剪切应力变化情况反映了桶体内流体流动性,因而在同一流速比下,表观黏度越均一,所反映的桶内流体流动性越好。

图14 不同流速比下表观黏度随桶体高度变化Fig.14 Variation of apparent viscosity with drum height for different velocity ratios
综上所述,增强桶体内湍流动能耗散率,减小平均最小涡尺度可有效强化不同密度煤泥水间的混合过程,增大细微颗粒碰撞概率。桶体下部区域湍流强度强于桶体上部,因而增大桶体下部区域体积对煤泥水混合具有强化作用,为增大桶体下部区域体积可使侧入料口和出料口的位置可适度上移,增大入料口与水平方向的夹角可使侧入料口入料煤泥水更充分进入桶体下部。为避免侧入料口入料短路直接从出料口流出,出料口位置应高于入料口位置;为避免上入料口入料短路直接从出料口流出,应适当加大出料口之间距离。从模拟结果看,上-侧入料流速比大于1.4,且侧入料流速至少为1.26 m/s 时混合效果较好,即上-侧入料质量流量比至少应大于1.28∶1。
2.3 颗粒分布
混料桶内部流场变化形成的湍流涡是导致流体内颗粒混合碰撞的主要原因之一,如图15 对各上-侧入料流速比在X-Z面正视视角上不同时刻颗粒及对应涡在混料桶内的分布分析,并对各入料口进入桶体的各种颗粒进行着色,由于进料口2 和进料口3对称分布所以只对进料口2 颗粒进行区别着色。

图15 各流速比不同时刻颗粒及对应涡在混料桶内的分布Fig.15 Distribution of particles and corresponding vortices in the mixing drum at different inlet fluid velocity ratios
结果显示,当vup∶vside为1.258∶1.258 时,颗粒进入桶体1.4 s 时的局部放大图中,颗粒在湍流宏观涡中移动的速度顺序:大粒度大密度>大粒度小密度>小粒度大密度>小粒度小密度。由于侧面入料口和出料口的影响导致的二次涡对颗粒的作用力导致颗粒向涡周边移动。在有旋流中,颗粒会始终沿着流线的切线方向移动,因而根据颗粒在宏观涡中的移动速度顺序,颗粒在涡流中具有一定速度梯度,并使大部分颗粒向同一方向移动,可增强颗粒碰撞和聚集效率。
当vup∶vside为1.882∶1.258 时,从上入料口进入的细微颗粒能够充分进入桶体下部,当vup∶vside为1.258∶1.258 和1.882∶1.870 时,入料流速比基本不变,仅实际流速增大,从结果可以观察到两种实际流速比下颗粒分布基本一致,说明不改变流速比,只改变流速大小对颗粒在桶内分布没有太大影响。而vup∶vside为1.258∶1.870 时,从上入料口进入的颗粒几乎不能进入桶体下部,而从侧入料口进入的颗粒也几乎全部进入桶体下部区域,vup∶vside为1.882∶1.258 时,从上入料口进入的颗粒可以进入桶体下部区域,而从侧入料口进入的颗粒也能有效分布于桶体上部区域和下部区域,且从图15 中vup :vside=1.882:1.258,t=5.8s 时的情况反映出颗粒有较好的团聚现象。
3 结论
1)相互垂直的流体进入混料桶内发生交会后,可诱导产生发卡涡、展向涡和轴向涡,涡-涡之间、涡-主流之间的交互作用显著提高湍流动能、降低涡尺度;随着上-侧入料流速及流速比从1.258∶1.870增大至1.882∶1.258,当上入料口入料密度大于侧入料口入料密度时,湍流动能和湍流耗散率缓慢增大,高湍流作用区域范围增大,平均最小涡尺度由68.33 μm增大至73.59 μm。当上入料口入料密度小于侧入料口入料密度时,湍流动能和湍流耗散率减小,高湍流作用区域范围减小,平均最小涡尺度由84.23 μm 增大至103.79 μm。当流速比相近,仅流速增大时,湍流动能和湍流耗散率增大且湍流耗散率变化比湍流动能变化更快,最小涡尺度减小。因此增大流速,降低上-侧入料流速比可有效减小最小涡尺度,且最小涡尺度主要以小于平均最小涡尺度的涡为主。
2)在同一流速比时,上入料口入料密度大于侧入料口入料密度的情况下,混合均匀性和混合效果均优于上入料口入料密度小于侧入料口入料密度的情况,更有利于流体混合及颗粒碰撞。当上入料口入料密度大于侧入料口密度时,流速比在0.67~0.7、1.0~1.1、1.40~1.50 时桶内密度分布较为均匀,上-侧入料流速比在1.40~1.50 时,桶体内表观黏度最为均匀,因而此流速比下桶内流体剪切应力随桶高变化不大,有利于不同密度流体混合。
3) 颗粒在湍流宏观涡中移动的速度顺序:大粒度大密度>大粒度小密度>小粒度大密度>小粒度小密度,使得颗粒在涡流中具有一定速度梯度,并使大部分颗粒向同一方向移动,可增强颗粒碰撞和聚集效率。模拟结果反映上-侧入料流速比大于1 时颗粒在混料桶桶体内分布比上-侧入料流速比小于1的分布更为均匀,并且上-侧入料流速比较大时有更好的颗粒团聚效果,因而适当增大上-侧入料流速比有助于流体混合及颗粒聚集碰撞。

