多技能资源能力不均衡环境下项目调度的鲁棒优化方法

胡振涛，崔南方

(1.湖北经济学院 工商管理学院，湖北 武汉 430205；2.华中科技大学 管理学院，湖北 武汉 430074)

资源受限项目调度问题 (resource constrained project scheduling problem, RCPSP) 以最小化项目工期[1-2]、最大化净现值[3]或计划鲁棒性[4]等为目标，在确定或不确定环境下构建一个满足资源和工序约束的调度计划。由基础RCPSP 可以延伸出若干项目调度问题，如多模式的RCPSP[5]、活动可中断的RCPSP[6]、柔性资源约束的RCPSP[7]等，其中，多技能项目调度问题 (multi-skilled project scheduling problem，MSPSP) 成为近些年研究的热点。它与传统RCPSP的主要区别在于所涉及的资源可以具备多项技能，能以不同的技能形式参与到不同的活动中去，因此资源与活动会存在多种对应关系。在进行多技能项目调度时，不仅要决定活动的开始时间及资源在活动间的分配，还要决定资源以何种技能参与其中，解的维度增加，问题变得更加复杂。

关于MSPSP 的研究多以工期最短为目标，并以元启发式或启发式算法求解，如蚁群算法[8]、混沌粒子群算法[9]、杂草入侵算法[10]、基于启发式规则的分支定界算法[11]、基于规则的启发式算法[12]等。在资源能力方面，大多假设资源的能力是均衡的，也即资源对每个技能的执行能力都取值于{0,1}，表示资源或是完全掌握该技能 (技能效率为1)，或是完全不掌握该技能 (技能效率为0)。也有部分学者考虑分等级的资源能力[13]，即根据执行能力的高低将资源分为不同等级，其中，高等级的资源可以执行低等级的技能；反之，则不然。

然而，在实际项目中资源对技能的掌握程度有时并不能用几个简单等级进行描述，其差异的大小可能取值于[0,1]上的任何数值，并且多个低能力的资源合力可以完成一项高能力需求的任务。例如在软件开发、设备维修等领域，多个不熟练的员工合力能完成一个熟练工的工作，多台低效设备同时运行能赶上一台高效设备的生产速度等。本文称这类资源为能力不均衡的多技能资源，它将资源能力的二元假设拓展到多元，使之更具一般性。

此外，项目的执行过程存在各种不确定因素，这些随机干扰会导致项目的实际进度难以完全符合预先制定的调度计划，而与计划不符的进度往往会增加项目的执行成本。为解决这一问题，学者们提出鲁棒性项目调度，即在制定计划时便考虑项目风险，从而生成一个抗干扰能力强的调度计划。然而目前关于鲁棒调度的研究多关注于单一技能资源受限项目，一旦考虑多技能资源尤其是能力不均衡的多技能资源，一般项目的鲁棒调度方法虽然也可使用，却由于忽略了资源的特点，并不能取得较好的结果。

基于以上背景，本文研究多技能资源能力不均衡环境下的鲁棒性项目调度问题 (multi-skilled project scheduling problem with uneven resource capacity，URC-MSPSP)。该问题的求解分为两个阶段：第1阶段通过基于规则的启发式算法求解基准调度计划；第2 阶段，在基准调度计划中插入时间缓冲，并根据资源特点对资源分配进行重新调整以提高调度计划的鲁棒性。

1 问题描述

项目网络采用节点式 (AON) 表示，共包含n个节点，起始节点1 和终止节点n代表虚活动；活动之间存在工序约束；以G= (V,E) 表示项目网络，其中，V= {1,2,···,n}表示活动集合，E为有向弧，表 示活 动的 工序 约束，以Pj表 示 活动j的前 序活 动的集合；资源具备多技能，每个资源都至少具备一种项目所需求的技能，R= {1,2,··· ,K}及F= {1,2,···,L} 表示资源和技能的集合，其中，资源总数为K，技能种类为L；用 R Fkl表示资源k执行技能l时的效率， R Fkl∈[0,1] ； 用TFil表示对技能l的需求量；活动i的工期是一个期望值为di的随机变量。结合URC-MSPSP 的特征，本文所研究问题的前提假设如下。

1) 资源是可更新的，且活动一旦开始，不可中途中止或更改资源分配方案；

2) 每单位的技能需求可以由多个资源合作执行，如1 单位的技能需求可由一个技能效率为0.6 和一个技能效率为0.4 的资源合作完成；

3) 过量的技能供应不能使活动的工期更短，例如一个需要1 单位技能的活动，若由一个效率为1 的资源单独完成时，其工期为3，则由两个技能效率分别为0.8 和0.3 的资源合作完成时工期亦是3。

为了进一步说明本文所研究的问题，引入算例(I)，其项目网络如图1 (a) 所示。其中，1 和4 为虚活动，2 和3 为实活动。项目需要2 种技能，各实活动的技能需求及期望工期分别标注在节点的上方和下方，项目的可用资源数量为5，资源的技能效率如图1 (b)所示。其中，R1～R5表示资源1 到资源5；F1和F2表示技能1 和技能2。可以看出，其中部分资源具备多技能，且资源能力不均衡，如资源R1在执行技能F1时其效率为0.2，而 在 执 行 技 能F2时其效率为0.5。图1 (c) 和图1 (d) 为两个可行的调度计划，每个矩形内的第1 个数字表示相应资源所参与的活动，第2 个表示该资源在该活动中所执行的技能。对比图1 (c) 和图1 (d) 可以看出，资源在活动间的分配以及资源在技能间的转换都会影响项目调度计划的工期。

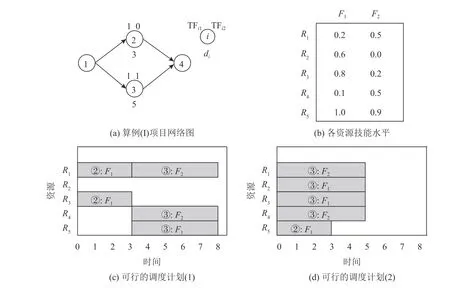
图1 项目算例 (I) 的相关参数Figure 1 Parameters of project instance (I)

在该算例中，对项目进行排程时，各活动的工期被视为确定值。因此在项目的执行进程中，一旦活动工期出现变化，实际进度便可能会与调度计划偏离，从而产生额外的执行成本。鲁棒性项目调度便是一种能有效应对这种风险的方法，它能在工期出现变动的情况下，使项目进度尽可能与原计划相符。基于此，本文的最终目的是在活动工期不确定环境下，针对多技能资源受限且资源能力不均衡的项目，生成一个具有较高鲁棒性的调度计划，以尽可能地最小化项目因不确定风险而产生的额外执行成本。

2 算法设计

2.1 确定环境下的基准调度计划求解

现有文献关于能力均衡的MSPSP 有较多的研究，求解方法主要有两种：元启发式算法，启发式算法。其中，元启发式算法虽然求解质量较高，却需要较长的求解时间，尤其在求解活动数量较多的复杂项目时，得到满意解所需要的运行时间往往是难以接受的。因此本文设计了基于规则的启发式算法以快速求解基准调度计划，算法1 展示了该算法的伪代码。

算法1: 基于规则的基准调度计划求解算法输入：项目活动V，工序关系E，活动的期望工期d，资源及技能相关参数等1 初始化： ， ， ， ， ，输出：基准调度计划中各活动的开始时间S t ←0 Vct Vp t Vst Vut w(t)card(Vut )＞0 2 while then card(Vst)＞0 3 while then 4 根据活动优先规则，选择优先权最高的活动i建立0-1 规划模型，求解活动i 的资源分配方案5 if 有解 then S i ←t Vst ←Vsti Vp t ←Vp t ∪{i}6 ， ，7 else Vst ←Vsti Vp t ←Vp t ∪{i}8 ， S 9 endif 10 endwhile t ←t+1 Vct Vp t Vst Vut w(t)11 更新 ， ， ， ，12 endwhile 13 return S

算法采用并行调度的方式，从时刻0 开始，在每个时间点t，将项目的所有活动分为4 个子集：已完工活动、正在进行中的活动、可排活动、不可排活动。其中，任意两个子集的交集为空集Φ，4 个子集的合集为项目活动集V。在算法1 中，w(t) 表示在时刻t各资源的权重的集合；Si表示活动i在调度计划中的开始时间。

2.1.1 活动优先规则

对于可排活动集Vts中的活动而言，所有紧前工序都已完工，即其满足所有的工序约束。然而由于资源可用量受限，Vts中的活动往往不能全部同时开始，这就需要对活动进行排序，以便有选择地开始部分活动，剩余活动则留作下一次迭代再行判断。现有文献中有较多关于活动优先规则的研究，本文选择和构造了以下5 种优先规则。

1) 随机选择 (random ranking, RR) ：活动随机进行排序。

2) 最晚结束时间 (latest finish time, LFT) ：活动按照最晚开始时间从早到晚排序。

3) 紧后活动总数 (total successors, TS) ：活动按照紧后活动 (直接和间接) 的总数量从大到小排序。

4) 技能需求度 (skill demand degree, SDD) ：活动按照对技能的需求程度 S DDi从小到大排序，SDDi用活动i的技能需求量与资源技能供应量的比值表示，赋值方式为

5) 最 大 分 级 位 置 权 重 (greatest rank positional weight, GRPW) ：根据活动及其所有直接、间接紧后 活 动工期之和 G RPWi从大到小 排 序，Wi表示 活动i的直接和间接紧后活动集，则

2.1.2 资源权重规则

按照活动优先规则选定活动后，就需要为活动分配资源。本文算法结合资源权重与0-1 规划模型以分配资源，一共考虑5 种权重计算规则。

1) 静态资源权重[12](static resource weight, SRW)，赋值方式如下。

2) 动 态 资 源 权 重 (dynamic resource weight，DRW)，赋值方式如下。

2.1.3 0-1 规划求解资源分配

在算法的每次迭代中，按照活动优先规则选择一个活动i，而后根据资源权重构建0-1 规划模型对其资源分配进行求解。

式 (5) 为目标函数，表示最小化当前所使用的资源的总权重。其中，xikl=1 表示资源分配，当资源k以 技 能l分 配 给 活 动i时xikl=1 ， 否 则，xikl=0 。wk为资源k的权重。当采用不同的资源权重规则时，目标函数便具有不同的现实意义。例如，当采用静态资源权重时，尽量不使用对整个项目更重要的资源；当采用动态资源权重时，尽量不使用对未排活动更重要的资源；当采用等权重时，在开始一个活动时尽可能少地使用资源。约束 (6) 为资源的可用量约束，Xkt表示资源k的当前可用量。约束 (7)为活动的技能需求约束。约束 (8) 为决策变量的取值范围。

2.2 不确定环境下的调度计划鲁棒优化

鲁棒性项目调度最常见的两种策略是设置时间缓冲和鲁棒性资源分配。据此，本文的鲁棒优化算法分为两部分：(1)从时间角度，向基准调度计划插入时间缓冲；(2)从资源角度，对已插入时间缓冲的调度计划进行资源的鲁棒优化。

2.2.1 基于时间的鲁棒优化方法

文献[14]提出一种基于风险估计的缓冲设置方法，即STC (starting time criticality)。它以最小化整个项目的总 stc 值为目标，逐步向基准调度计划中插入缓冲，每次迭代选择在stc值最高的活动前插入一单位的时间缓冲，直至整个项目的总 stc 值不再降低或计划工期达到项目期限为止。活动j的 stc 值为

其中，cj为活动j延迟一单位时长的惩罚成本；SEj、S j分别为活动j的实际开始时间和计划开始时间；γ(SEj＞S j)表 示活动j延迟的概率。

尽管很多文献证明STC 求解鲁棒调度计划的优越性，但它仍存在以下缺陷。(1) STC 在计算活动j的延迟概率时，考虑了活动j所有直接和间接紧前活动对它的推迟效应，并累加所有推迟效应以表示其延迟概率，然而在应用中这种累加会导致部分推迟效应被重复计算，导致延迟概率被放大，且紧前活动越多的活动延迟概率被放大的程度就越高。(2) STC 在每次迭代中，都以类似贪婪算法的方式选择在期望惩罚成本最大的活动前插入缓冲，然而项目调度的鲁棒优化问题并不具备最优子结构性质，这种短视的插入方法并不是最好的寻优方式。此外，STC 法是基于单技能资源受限项目调度问题设计的，虽然也可用在URC-MSPSP 中，却忽视了能力不均衡的多技能资源所引起的相关变化。基于此，本文提出改进的STC 鲁棒优化算法，伪代码如算法2 所示。

算法2: 改进的STC 算法输入：基准调度计划S，活动工期分布函数CDF，活动延迟惩罚成本c，项目期限Duetime Sr 1 初始化： ,输出：插入缓冲后的鲁棒调度计划Sr ←S c ←1通过Monte-Carlo 模拟，求解各活动的延迟概率Sr stc根据延迟概率和延迟惩罚成本求解 下各活动的c=1 2 while then c ←0 V′←V 3 ，card(V′)＞0 4 while then stc V′5 根据 用轮盘赌的方式，从 中选择活动i，将其开始时间延迟一单位，并将相关紧后活动的开始时间也延迟一单位，得到S′调度计划S′ stc′6 求解 下各活动的∑stc′＜∑stc max(S′)≤Duetime 7 if && then c ←1 Sr ←S′ stc ←stc′8 ， ，9 break 10 else V′←V′i 11 12 end 13 end rand(1)＜pm 14 if then V′←V 15 card(V′)＞0 16 while then 1/stc V′17 根据 用轮盘赌的方式，从 中选择活动j，将其开始时间提前一单位，并将相关紧前活动的开始时间也提前一单位，得到调度计划S′′S′′18 if 不违背工序及资源约束 then 19 ，计算 中各活动的 ，Sr ←S′′ S′′ stc′′ stc ←stc′′break 20 end 21 end 22 end 23 end Sr 24 return

1) 基于Monte-Carlo 模拟的活动风险估计。

2) 缓冲的有偏随机插入法。

在传统STC 法中，缓冲总是以贪婪的方式插入到具有最大 stc 值的活动前。本文提出有偏随机插入缓冲的方式。所谓有偏，就是插入缓冲时更偏向于选择 stc 值 大的活动，同时， stc 值小的活动也有被选择的可能。这一过程在算法2 的4～13 行执行，即根据各活动的 stc 值，按照轮盘赌的方法选择所要插入缓冲的活动，其中，活动j被选择的概率为stcj/

3) 缓冲的有偏随机回退法。

在传统STC 法中，随着迭代的进行缓冲不断增加，而没有减少的过程。改进的STC 则借鉴了爬山算法的思想，在每次迭代中以一定的概率pm，减少某个活动前所插入的缓冲。这一过程在算法2 的14～22 行执行，其中活动的选择也是有偏随机的，值得注意的是在缓冲插入过程中，新的调度计划只有在其总期望惩罚成本低于前一次迭代的调度计划时，才会被接纳为新解，而在缓冲回退过程中，只要新的调度计划满足工序及资源约束，便会被接纳。活动j被选择的概率为

2.2.2 基于资源的鲁棒优化方法

本文从资源弧优化和资源合作优化两个方面，对资源进行鲁棒性调整。

1) 资源弧优化。

资源弧是指由于资源的流向而在两个活动之间形成的先后约束关系，与工序约束不同，资源弧约束是可变的，它随着调度计划及资源分配的变化而发生改变。资源弧会为项目活动增加额外的约束，从而导致调度计划的鲁棒性降低。对一个项目而言，最好的资源分配方案是尽可能地减少与工序约束不重合的资源弧。调度计划在经过算法2 的缓冲插入以后，活动时间窗的重叠会减少，这也为资源调整提供了基础。算法3 展示了资源弧优化算法的伪代码。

算法3: 资源弧优化算法输入：已插入缓冲的调度计划Sr Srr输出：经过资源弧优化的调度计划Srr ←Sr Srr stc 1 初始化： ，求解 下各活动的i=1 →n 2 for do i 3 if 在活动 的时间窗内存在可调换的资源 && 调换以后能减少活动之间的约束 then S′4 调换相关资源，得到调度计划S′ stc′5 求解 下各活动的∑stc′＜∑stc 6 if then Srr ←S′ stc ←stc′7 ，8 end 9 end 10 end Srr 11 return

2) 资源合作优化。

在多技能资源能力不均衡环境下，活动的技能需求有时会需要多个资源合作才能满足。以前文中引入的算例 (I) 为例，图1 (c) 所示的调度计划中，活动2 对技能F1的 需求 便是由资源R1和R3合作执行的。在插入缓冲以后，调度计划中的空闲时间窗会将原本不可被某活动使用的资源变为可用。这里的做法是尽可能少地使用资源，从而达到减少活动间资源流约束的目的。算法4 展示了这一过程的伪代码。

算法4: 资源合作优化算法Srr输入：调度计划SR输出：最终的鲁棒调度计划SR ←Srr SR stc 1 初始化： ，求解 下各活动的i=1 →n 2 for do i 3 if 在活动 的时间窗内存在空闲资源 then S′4 通过0-1 规划求解资源分配方案，得到新的调度计划 ，其中资源权重的计算方法为等权重法 (ERW)S′ stc′5 求解 下各活动的∑stc′＜∑stc 6 if then SR ←S′ stc ←stc′7 ，8 end 9 end 10 end SR 11 return

3 数值实验

所有算法用Matlab R2017b 进行编写，测试平台为Windows 10 操作系统，处理器为Intel (R) Core (TM)i3-6100 3.70GHz，内存4.00G。

3.1 算例库

本文参考文献[15]提出的多技能项目算例生成方法，结合URC-MSPSP 的特点，生成4 个算例集J30、J60、J90 和J120，其中的项目算例分别包含30、60、90 和120 个实活动，每个算例集包含108个算例，整个算例库共432 个算例。每个项目所涉及的技能有4 种，其中的资源具备多技能，且技能能力不均衡，即 R Fkl∈[0,1] 。此外，还考虑以下两个项目参数。

1) 网络复杂度 (network complexity, NC) ：代表项目网络的复杂程度，以活动的平均紧后工序数表示， N C ∈{1.5,1.8,2.1} ；

2) 需求因素 (requirement strength, RS) ：代表活动对技能的需求强度，以活动平均需求的技能种类数与技能总种类数的比值表示，例如，当RS = 0.5时，表示项目中活动的执行平均需求 4 ×0.5=2 种技能， R S ∈{0.25,0.5,0.75,1} 。

3.2 实验设计

为了研究项目不确定性的影响，本文对活动工期设置了低、中、高3 种不确定风险水平。活动工期服从对数正态分布，以 σd表示活动工期的标准差， σd∈{0.3,0.6,0.9} 。一个期望工期为3 的活动。3种风险环境下的工期的概率密度函数曲线如图2所示，其中，横轴表示活动工期；纵轴f(d) 表示工期等于d的概率。

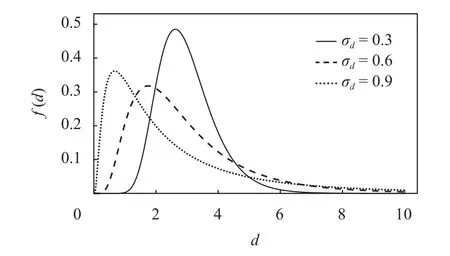
图2 E (d)=3 的活动在3 种风险水平下的工期分布Figure 2 Distribution functions for activities with E(d)=3under three risk levels

参考文献[14]，在仿真实验中将项目的工期期限设为基准调度计划工期的1.3 倍，各活动每偏离计划一单位时间的边际惩罚成本c从[0,1]中随机产生，项目每超过工期期限一单位时间的惩罚成本为。实验以项目的总惩罚成本为评价调度计划鲁棒性的最终指标，则项目算例z仿真的总惩罚成本为

3.3 结果分析

3.3.1 基准调度算法实验结果分析

求解基准调度计划的关键步骤有两个，即活动排程和资源分配，分别对应前文中的活动优先规则及资源权重规则。表1 汇总了本文所研究的相关规则，从中可以看出在求解基准调度计划时，共有25 种规则组合可供使用。以算例库所有算例为实验对象，本文测试了全部的规则组合，实验结果如图3所示。其中，横坐标表示规则组合；纵坐标表示各算例集求得的平均工期。

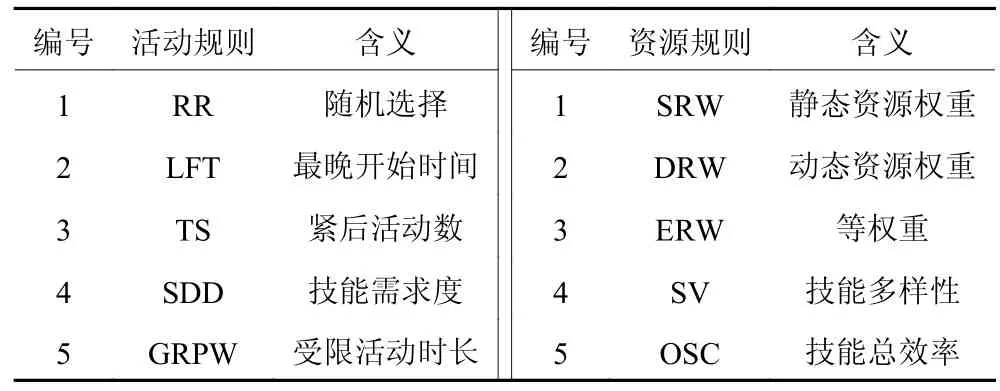
表1 活动与资源规则汇总Table 1 Activities and resource rules

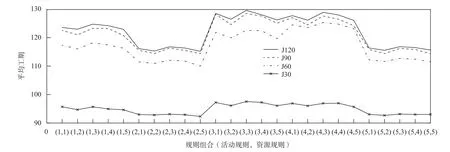
图3 4 个算例集在25 种规则组合下的平均工期Figure 3 The average makespans of four instances under 25 rule combinations

由图3 可知，在4 个算例集中，各参数组合的整体表现趋势几乎相同，其中最优的参数组合为(2,5)，也即活动按照最晚开始时间排序，资源权重大小等于资源的技能总效率 (LFT, OSC)。这与文献[14]在求解能力均衡条件下的MSPSP 所得的结果 (LFT, SRW) 不同。这是因为在能力不均衡环境下，资源不仅存在技能种类上的差异，还存在着执行效率的差异，资源效率的影响变得更为突出，从而导致在传统MSPSP 中表现较好的资源规则SRW 在URC-MSPSP 中的表现差于表示资源技能总效率的规则OSC。

3.3.2 鲁棒优化算法实验结果

由算法2 可知，鲁棒优化过程中有两个会影响算法效率的参数：Monte-Carlo 模拟次数Tmc和缓冲回退概率pm。为校正这两个参数，本文选择算例库部分算例作为测试集。结果表明，随着Tmc和pm的增大，解的质量会提高，但同时算法的运行时间也会相应变长。通过权衡算法的求解质量和求解时间，本文设

在最终的仿真实验中，首先通过基于优先规则(LFT, OSC) 的启发式算法求解每个算例的基准调度计划。在3 种风险水平下，分别用文献[14]的STC法、本文提出的无资源调整过程的改进STC 法(iSTC) 与含有资源调整过程的改进STC 法 (iSTCr)，对基准调度计划进行鲁棒性优化。最后经过 3 000次仿真模拟，求解各算例的TPC，结果汇总如表2所示。

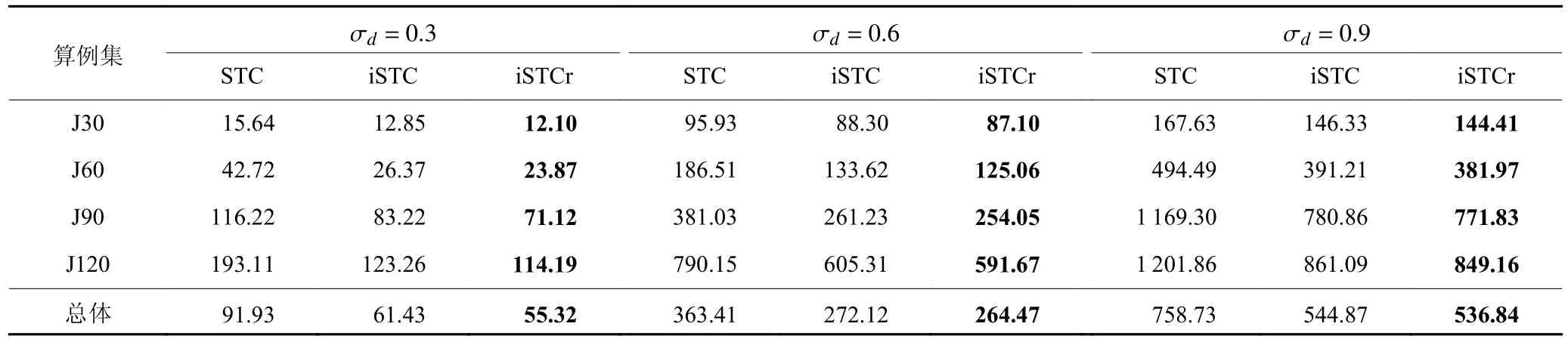
表2 各风险水平下不同算法求解的平均C TPTable 2 The average C TP under different risk levels obtained by different algorithms

由表2 可以看出，随着项目规模及风险水平的升高，项目的总惩罚成本也逐渐增加。这是因为在制定计划时，不可能预测到未来的全部情况，无论如何考虑鲁棒性，都不能完全消除不确定因素的影响。项目规模越大、风险水平越高，不确定因素就越多，所引起的惩罚成本也就越高。此外，对比3 种鲁棒优化算法可知，在不同的项目规模及风险水平下，其所求得的TPC 大小顺序都是一样的，即STC ＞iSTC ＞ iSTCr。这证明有偏随机缓冲的插入与回退以及资源的调整过程都是有效地提高调度计划鲁棒性的方法。

4 结束语

在活动工期不确定的环境下，URC-MSPSP 的鲁棒调度具有不同于传统RCPSP 的特点。相较于传统RCPSP，URC-MSPSP 中资源能力的不均衡使其求解调度计划变得更加困难，但同时资源间更加灵活的替代、合作关系也为鲁棒优化提供了更多的调整空间。基于此，本文提出基于优先规则的基准调度计划求解算法，以及考虑时间缓冲设置和资源调整的鲁棒优化算法。仿真实验的结果表明，相较于传统的鲁棒优化方法，本文所设计的算法能更加有效地提高调度计划的鲁棒性。本文的主要贡献有以下3 点：1) 设计了求解URC-MSPSP 基准调度计划的启发式算法；2) 从时间缓冲视角，引入缓冲的有偏随机插入及回退过程，设计了基于时间的调度计划鲁棒优化算法；3) 根据多技能且能力不均衡的资源的特点，从资源弧调整和资源合作调整两个方面，设计了基于资源的调度计划鲁棒优化算法。