改进的包裹圆算法提取建筑立面轮廓
张睿,余代俊
1. 成都理工大学 地球科学学院,成都 610059;
2. 广东省建筑设计研究院有限公司,广州 510010
1 引 言
三维激光扫描技术可快速获取扫描对象的表面点云数据,基于点云数据对物体进行三维重建是当前三维重构的研究热点(程效军和方芳,2014;张娟等,2018)。
对于完整的三维点云,提取其边界通常需要将其分割为若干个面片后对各个面片进行边界提取。王琼等(2017)认为点云边界特征是物体重要的几何特征,对三维重构起着重要作用。Previtali 等(2014)提出了一种高度自动化的方法,该方法首先将建筑立面的点云分割为平面元素,然后利用一些先验知识从识别的平面簇中自动提取立面隔断线以供之后生成模型。部分研究借助霍夫变换实现点云的分割,Song 等(2019)利用三维霍夫变换实现了大规模点云的地面提取;Widyaningrum 等(2019)提出有序点辅助霍夫变换(ordered pointsaided Hough transform,OHT)算法,该算法使用有序建筑物边缘点辅助霍夫变换,进而从机载激光雷达(light detection and ranging,LiDAR)点云中高质量地提取出建筑物轮廓。闻平等(2020)提出渐进式建筑物轮廓线提取方法,该方法先通过渐进数学形态学滤波分离非地面点,然后使用改进的三维霍夫变换分类出建筑物点云,进而提取建筑物轮廓点。霍夫变换的稳健性较好,抗噪性较强,但计算量较大,对于稀疏点云可用,但较稠密的点云不太适用该方法。Mineo 等(2019)提出利用邻域点特征来提取边界点,优点是能跳过分割直接提取完整的三维点云轮廓。对于分割后的点云,常用的边界提取方法有图像法、区域增长算法、alpha-shapes算法等。邹纪伟等(2020)通过将点云内插为深度图像,使用图像边缘检测方法提取边界。霍芃芃等(2019)指出基于影像的自动化提取方式不需要人工干预,效率较高。该方法的缺点是点云转换影像在重采样过程中会丢失细节特征,导致提取边界精度较低。赵传(2017)将区域增长算法应用于建筑物屋顶面轮廓提取,但该算法对数据噪声、数据缺失敏感。詹曦和张建生(2013)使用基于三角网格的边界提取算法,但由于涉及转换三角网格模型,时间成本较高。alpha-shapes 算法是近年较为常用的一种提取点云边界的算法。沈蔚等(2008)将该算法应用于LiDAR 点云建筑物轮廓的提取,成功提取出了各类凹凸多边形轮廓线。廖中平等(2019)提出了一种可调节滚动圆半径的alpha-shapes 平面点云边界提取算法,该算法具有良好的稳健性。伍阳等(2021)提出了一种可自适应变换滚动圆半径的alpha-shapes 算法,能够有效提取机载LiDAR 建筑物点云顶部轮廓,具有较高的提取效率和良好的稳健性,提取的轮廓精度较高。针对alpha-shapes算法运算速度慢的缺点,聂玉泽等(2016)提出了包裹圆算法提取LiDAR 点云的边缘点,并给出了包裹圆半径的经验值。但包裹圆算法仅对密度均匀的点云有较好的适应性,当点的密度分布不均匀或点的密度未知时,包裹圆算法难以确定包裹圆半径及包裹圆内部点数的阈值。
本文针对上述包裹圆算法难以确定包裹圆内部点数阈值的问题,提出了改进的包裹圆算法,以方位角为基准将包裹圆划分为若干区域,以每个区域内是否都存在点为条件,判断各个点是否为边界点,避免了阈值选取问题,且无须依赖点云密度确定包裹圆半径。
2 包裹圆算法边缘点提取
对于建筑物立面点云,提取其轮廓线步骤为:首先,将立面从建筑物点云中提取出来,其次,通过旋转算法将立面点云旋转至与某一坐标面平行,一般旋转至与XOY面平行,旋转后的立面点即可以用X、Y坐标显示;再次,利用边缘点提取算法对建筑物的边缘点进行提取;最后,将提取出来的边缘点拟合,形成建筑物的轮廓线。
2.1 包裹圆算法原理
包裹圆算法通过设定一个半径r及包裹圆内点数阈值h,以点云内每个点为圆心作半径为r的圆,称为包裹圆,并统计包裹圆内点的个数:若包裹圆内点数大于等于h,则判断该点为内部点;否则为边缘点。以图1 矩形为例,在边缘部分以边缘点为圆心形成包裹圆,包裹圆内圆心角有180°范围内没有点的存在,角点处有270°范围内没有点的存在,以1.5 倍点间距作为包裹圆的半径,理论上角点包裹圆会包裹4 个点,边缘点包裹圆会包裹6 个点,内部点包裹圆会包裹9 个点。利用落在包裹圆内部点数不同这一特征,可将边缘点提取出来。但对于未知密度或密度不均匀的点云,包裹圆算法很难确定阈值h及包裹圆半径r,需要不断人工尝试以确定,极大影响了算法的自动化程度。
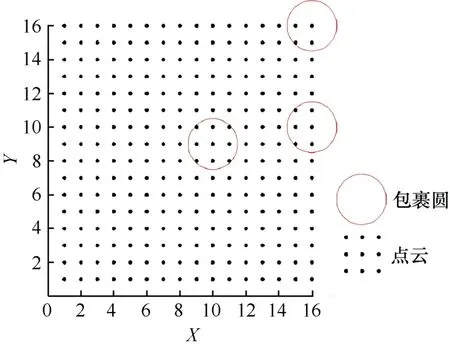
图1 包裹圆算法仿真示意图(单位:cm)Fig.1 Wrapping circle algorithm workflow(Unit:cm)
2.2 包裹圆算法步骤
包裹圆算法输入参数为包裹圆半径r及包裹圆内部点数阈值h,当某点的包裹圆内部点数大于h时,判断该点为内部点;反之则为边缘点。算法流程,如图2 所示。
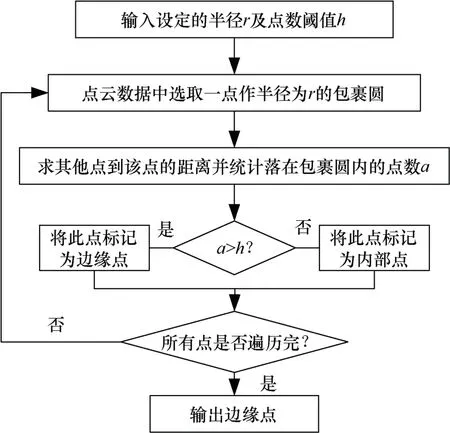
图2 包裹圆算法流程Fig.2 Wrapping circle algorithm process
3 改进的包裹圆算法
改进的包裹圆算法将包裹圆按照方位角θ划分为若干个区域,通过判断各个区域内是否都存在点进而判断边缘点。对于内部点而言,包裹圆的各个区域必然都存在点,但边缘点的包裹圆会有若干个区域不存在点。因此,若某点包裹圆内各个区域都存在点,则判断其为内部点;反之则为边缘点。
3.1 改进算法步骤
有别于alpha-shapes 算法与包裹圆算法,改进算法可应用于建筑物整体的轮廓提取,而不局限于单个立面,即可用于提取三维点云的轮廓,而非仅适用于二维点云。
(1)对于单个建筑立面(二维点云),改进算法为:①创建kdtree,用于执行半径近邻搜索;②选取点云中一点,以其为圆心作半径为r的包裹圆,并将包裹圆等分为若干个区域,每个区域对应的圆心角为θ;③使用半径近邻搜索获取落在包裹圆内的点,并计算落在包裹圆内的点所在的区域;④判断包裹圆内各个区域是否都存在点,若都存在则包裹圆圆心为内部点,反之则为边缘点;⑤选取另一个点为包裹圆圆心,执行步骤②、③、④直至点云内所有点都遍历完毕。
(2)对于建筑物整体轮廓提取,实施步骤为:①使用随机采样一致性(random sample consensus,RANSAC)算法拟合建筑物中一个立面(赵烨等,2014;刘亚坤等,2021;邹鹏等,2020;Wu 等,2021)对应的平面A,获取该平面相对准确的参数解(雷经发等,2020),根据罗德里格斯旋转公式,计算将该平面旋转至与XOY面平行的旋转矩阵,根据得到的旋转矩阵旋转点云;②对点云使用上述提到的单个建筑立面轮廓提取的算法,该步骤会提取出建筑点云中所有与平面A平行立面的轮廓;③重复步骤①、②直至建筑物整体轮廓提取完成。
3.2 时间复杂度分析
(1)包裹圆算法主要步骤的时间复杂度分析。设点集内有n个点,对于算法的时间复杂度,每次迭代均需要计算包裹圆圆心与点集内每个点的距离,该步骤的时间复杂度为O(n);获取距离小于r的点数目a,该步骤的时间复杂度为O(n)。综上,包裹圆算法每次迭代的时间复杂度为O(n),由于点集内每个点都需要遍历,所以需要执行n次迭代,算法的总体复杂度为O(n2)。
(2)改进算法主要步骤的时间复杂度分析。建立kdtree 在迭代之前进行,时间复杂度为O(nlogn),进入迭代后,创建包裹圆的时间复杂度为O(1),可以忽略,半径近邻搜索的时间复杂度为O(n1-1/k+m),其中,k为kdtree 的维度,m为返回的点数目,计算包裹圆内各点与包裹圆圆心的位置关系的时间复杂度为O(m)。综上,改进算法每次迭代的时间复杂度为O(n1-1/k),算法的总体时间复杂度为nO(n1-1/k+m)。
根据两种算法的时间复杂度分析,当n较小时,两种算法的时间消耗应当大致相同,甚至在k较大而n较小时,包裹圆算法的执行时间可能小于改进算法;但随着n增大,改进算法与包裹圆算法的时间消耗会逐渐接近,当n足够大时,改进算法的时间消耗会远小于包裹圆算法。
4 实验与分析
研究以Matlab 为平台,以实际测量某建筑点云为实验数据。由于边缘检测算法对离群点和噪声十分敏感,在应用边缘检测算法时先对点云做降噪处理(巩育江等,2022)。
4.1 单个立面轮廓提取实验
实验用点云数据,如图3(a)所示。由于原始数据的点密度不均匀,难以使用包裹圆算法提取边缘点,所以包裹圆算法所用点云经过了体素降采样,采样距离设置为3 cm,取包裹圆半径为1.5 倍点间距,即4.5 cm,取阈值h=7,结果如图3(b)所示。改进算法可应用于密度不均匀的点云,所以直接使用原始数据进行处理,取包裹圆半径r=5 cm,θ=60°,结果如图3(c)所示。可以看出,由于经过降采样,包裹圆算法已经无法提取出点云内的门,且包裹圆算法提取的文字边缘略显模糊,改进算法提取点云轮廓的效果优于包裹圆算法,且包裹圆算法必须要应用在点密度均匀的点云上,否则很难确定算法的参数。
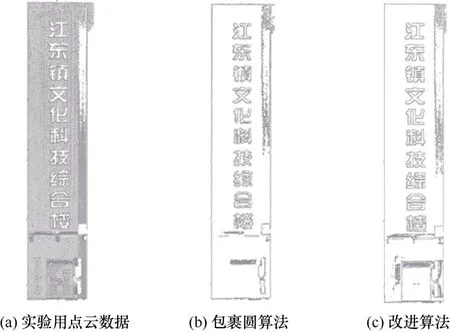
图3 基于点云数据的包裹圆算法和改进算法两种方法处理效果对比Fig.3 Comparison of the processing effects of the wrapping circle method and improved algorithm based on point cloud data
两种方法提取边缘点的耗时对比,如表1 所示。在点数较小的时候,改进算法耗时较包裹圆算法较长,此时两种方法耗时都较短;随着点数的增加,改进算法的耗时增长更慢,包裹圆算法耗时的增长较快,当点数足够大时,改进算法的耗时较包裹圆算法大大缩短。
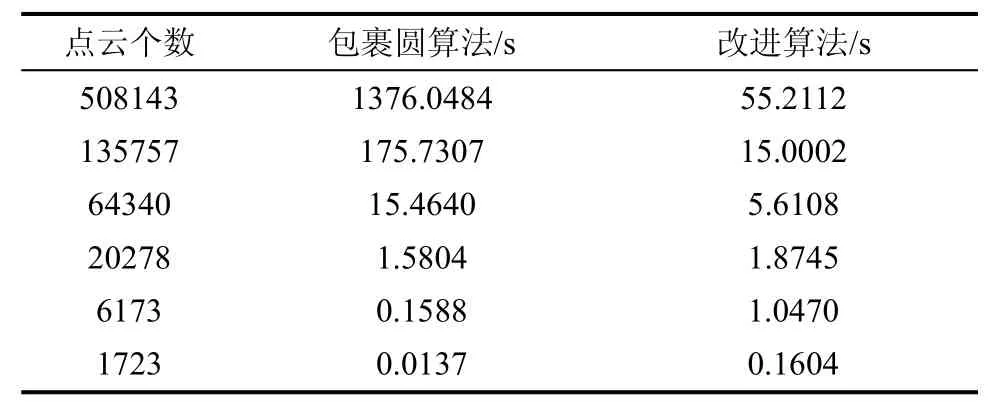
表1 两种算法提取边缘点的耗时对比Tab.1 Comparison of the time consumption between two methods
4.2 建筑物整体轮廓提取实验
通过反射率滤波将反射率较低的部分点(如玻璃窗户)滤除,研究使用预处理后的点云,如图4(b)所示。
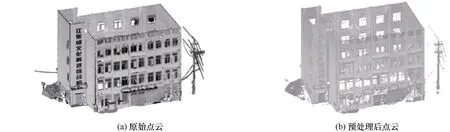
图4 实验用的原始点云和预处理后点云数据Fig.4 Original point cloud and preprocessed point cloud data used in the experiments
采用传统的先分割后提取方法与本文的不进行分割方法,分别进行建筑物的整体轮廓提取,实验结果如图5 所示。可以看出,存在凸起的墙体及一扇凸起的门,传统方法提取的轮廓中已丢失这些轮廓,本文方法可很好地保留这些细节;且传统方法在各个立面交线处有许多冗余的点,这可能是因为在立面分割过程中未能很好地处理交线处的点,本文方法避免了对交线处点的处理,大大减少了交线处的冗余点。
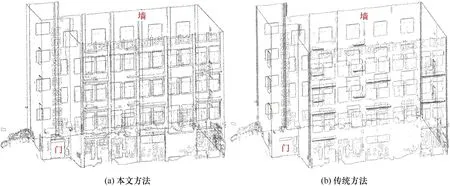
图5 本文方法与传统方法的实验结果对比Fig.5 Experimental comparison of the method in this article and traditional method
相较于传统轮廓提取算法,研究特点主要体现在:①建筑立面上通常会有凸起的物体,如空调、雨棚等,传统方法通过点云分割将立面点云分割出来后会将其投影为二维点云,在投影的过程中这些凸起的物体会丢失,导致提取出的轮廓丢失许多细节,改进算法提取轮廓可以很好地保留这些立面上的凸起物体,使提取的轮廓细节更完善;②传统方法需要通过点云分割将建筑物各个立面提取出来,提取出的轮廓受点云分割结果的影响较大,改进算法可规避点云分割这一步骤,避免点云分割结果对最终提取出的轮廓的影响且由于无需处理点云分割的成果,自动化程度更高。
5 结 论
针对包裹圆算法存在的,处理点的密度分布不均匀时,难以确定其包裹圆半径及点数阈值的问题,本文提出将包裹圆划分区域,通过针对区域内点的分布情况判断边缘点的改进算法。针对传统立面轮廓提取流程受点云分割结果影响较大的不足,提出了不进行点云分割的立面轮廓提取方法。实验表明:本文的改进算法不仅在效果上优于包裹圆算法,且自动化程度较高,当点云规模较大时,处理速度也明显优于包裹圆算法;对于建筑物整体的轮廓提取,本文方法能避免传统方法由投影带来的部分三维细节丢失问题及点云分割带来的立面交线处冗余点问题。

