Real-Time Optimal Control for Variable-Specific-Impulse Low-Thrust Rendezvous via Deep Neural Networks

，

College of Astronautics， Nanjing University of Aeronautics and Astronautics， Nanjing 211106， P.R.China

Abstract: This paper presents a real-time control method based on deep neural networks （DNNs） for the fuel-optimal rendezvous problem.A backward generation optimal examples method for the fuel-optimal rendezvous problem is proposed， which iterates through the dichotomy method based on the existing backward generation idea while satisfying the two integration cutoff conditions of the backward integration.We construct a DNNs structure suitable for the variable-specific-impulse model and divide the output control of networks into the thrust output and the specific impulse output.For the specific impulse output， a method is proposed that learns the optimal specific impulse first and then limits it according to its actual upper and lower limits.We propose the enhanced fault-tolerant deep neural networks （EFT-DNNs） to improve the robustness when approaching rendezvous.The effectiveness and efficiency of the proposed method are verified by simulations of the Earth-Apophis asteroid and Earth-Mars missions.

Key words：trajectory optimization； variable specific impulse； fuel-optimal control； indirect method； deep neural networks（DNNs）

0 Introduction

Electric propulsion （EP） is a quite promising propulsion method for deep space exploration missions， and there are already many examples of successful use of EP［1-4］.The thrust of EP is very small， usually less than 1 N， and it needs to be turned on continuously to get the work done［5］.The dynamic continuous low-thrust control poses great difficulties for trajectory optimization.Traditional methods for solving the low-thrust trajectory optimization problems are direct methods［6-7］and indirect methods［8-9］， and the combination of the above two［10］.The direct method is to solve the original problem by transforming it into nonlinear programming （NLP） with discrete series， while the indirect method is to transform optimal control problems（OCPs） into a two-point boundary value problem（TPBVP） by constructing co-states.Deep space exploration missions have a long period and long flight distance， with non-negligible communication time delay［11］.Considering the influence of uncertainty and other complex factors， the spacecraft needs to have the capability of autonomous trajectory optimization and real-time control.However， due to the limitation of onboard computing capability， the direct and indirect methods are computationally intensive and cannot meet the requirements of onboard real-time control.

With the progress of artificial intelligence technology， especially machine learning （ML）， in the field of spaceflight is gradually increasing， which provides the possibility of real-time control onboard［12］.Deep learning and reinforcement learning are currently the most popular ML techniques in the field of deep space exploration trajectory design and optimization.Deep learning is a kind of supervised learning.In the existing research， the optimal trajectory information， including the initial values of costates， fuel consumption， transfer time， thrust，etc.， is often obtained by methods such as indirect methods， and subsequently， DNNs are trained to learn the mapping relationship between inputs and outputs.Deep learning enables fast estimation of transfer costs［13-14］， fast optimization of trajectories and real-time control［15-20］.For the problem of rapid estimation of low-thrust transfer costs， Zhu et al.［13］achieved rapid assessment of low-thrust transfer accessibility and optimal fuel consumption prediction by a multilayer perceptron （MLP） in the context of the seventh edition of the Global Trajectory Optimization Competition （GTOC7）； Li et al.［14］used neural networks to achieve optimal time prediction；Viavattene et al.［15］applied neural networks to the rapid estimation of transfer times and costs for multitarget asteroid missions.For the difficulty of guessing initial values of co-states， Yin et al.［16］and Zhao et al.［17］proposed initial guessing methods based on neural networks for the interplanetary transfer and asteroid landing problems， respectively.However，for the real-time control， a more accurate way than guessing the co-states initial value is to use neural networks to complete the state-control mapping［17］.Cheng et al.［18］proposed a multiscale-DNN to achieve high accuracy transfer， and this network is for real-time control of the thrust direction angle.Li et al.［14］studied the time-optimal real-time control problem based on neural networks； Izzo et al.［19］solved the Earth-Venus fuel-optimal transfer problem and compared control effects of value function and policy function networks.Unlike deep learning，reinforcement learning is performed by discretizing control into a finite number of actions and later modeling the OCPs as a Markov decision process（MDP）.Optimal actions are explored through the payoff function， which leads to real-time optimal control［20］.However， reinforcement learning is good for simpler OCPs， but can hardly solve complex strongly nonlinear problems.In addition， increasing the number of control actions to obtain a more continuous control also makes the problem more difficult to solve.In this paper， we choose a deep learning approach to achieve OCPs of the spacecraft.

One of the important things of using deep learning is how to get the optimal dataset efficiently.Datasets are often generated by solving traditional lowthrust trajectory optimization problems， most commonly using indirect methods to generate datasets.However， solving low-thrust problems one by one is very time-consuming， and it is worthwhile to investigate how to improve the dataset generation rate.Considering the small difference between initial values of co-states of adjacent trajectories， Yin et al.［16］proposed a method based on the fast generation of optimal nominal trajectories， which used initial values of co-states of nominal trajectories as costates guesses of new trajectories.Liu et al.［21］proposed a data generation algorithm based on the optimal trajectory continuation method to improve the success rate of initial value guessing.However，these two methods for fast dataset generation are still essentially guessing initial values of co-states and then solving the TPBVP.Izzo et al.［19］proposed a method to satisfy the shooting equation for backward integration， which they called “the backward generation of optimal examples”， and successfully applied it to the fuel-optimal transfer problem.Since this method changes the solution time of the TPBVP into one backward integration time， the solution speed is greatly improved.Izzo et.al.［22］applied this method to the constant acceleration time-optimal control problem.However， the shooting equation for the fuel-optimal rendezvous problem is different from both the fuel-optimal transfer and the constant acceleration time-optimal problem， so it cannot be applied directly.Therefore， this paper proposes a backward generation method of optimal examples for the fuel-optimal rendezvous problem.

At present， deep learning methods used in realtime OCPs all aim at the fixed-specific-impulse problems［13-14，18-19］.In fact， the specific impulse of EP engines， including magnetic plasma rockets［23］，Hall effect［4］， and ion EP［1，3］， is variable.The variable-specific-impulse electric propulsion model is more in line with the engineering reality.In this paper， we consider the specific impulse as a controlled quantity that can be actively varied in the interval，where the engine input power is influenced by the distance of the spacecraft from the sun［24-25］.First，for the optimal trajectory generation， the introduction of variable-specific-impulse will make the trajectory optimization problem more complicated to solve.Second， when using DNNs for optimal control， it is worthwhile to find out how to perform the accurate control of the variable-specific-impulse.In the related literature［14，18-19，22］the control quantity of the deep neural network controller is one or two kinds of thrust direction and thrust size.The control quantity under the variable ratio impulse model is increased on this basis for the control of the ratio impulse， and the more the number of control quantities， the greater the possibility of error.How to improve and ensure the control accuracy is also worth considering.Based on the above research status，this paper studies the real-time OCPs of variablespecific-impulse low-thrust rendezvous based on DNNs.

The contributions and advantages of this paper are mainly in the following three aspects.Firstly， to address the problem that the backward optimal trajectory generation method in existing studies［19，22］cannot be used for fuel-optimal rendezvous trajectories， an backward generation optimal examples method applicable to the fuel-optimal rendezvous problem is proposed to improve the efficiency of data set generation.Secondly， since existing DNNbased research［13-14，18-19］is only for the fixed-specific impulse problem， not for the variable-specific-impulse problem， this paper proposes a DNN-based real-time control method for variable-specific-impulse， and constructs a real-time optimal control deep neural networks （RTOC-DNNs） to control the thrust and specific-impulse.For the thrust control， the Monte Carlo simulation accuracy of thrust learning in Cartesian and orbital coordinate systems is compared.For the specific impulse control，DNNs are proposed to learn the optimal specific impulse， and then the output is restricted by the upper and the lower bounds of the specific impulse.Finally， EFT-DNNs are proposed for enhancing the control robustness and rendezvous accuracy of the spacecraft in the second half of the flight， and the effectiveness of the EFT-DNNs are verified by simulations.

The structure of this paper is as follows.Section 1 introduces the variable-specific-impulse lowthrust model along with the fuel-optimal rendezvous problems and the optimality conditions are derived using the indirect method.Section 2 presents the backward generation for the fuel-optimal control rendezvous problem.Section 3 presents the network structure.In Section 4， nominal trajectories and data set generation are presented， followed by the RTOC-DNN and the EFT-DNN parameters selection and construction of the networks.In Section 5，the proposed methods are applied to the Earth-Apophis asteroid and Earth-Mars rendezvous missions，and the effects of DNNs are verified using Monte Carlo simulations.Section 6 concludes the paper.

1 Low-Thrust Trajectory Optimization

1.1 Dynamical model

We consider a spacecraft with a variable-specific-impulse EP engine， and this spacecraft moves in the gravity of the Sun.In the Cartesian coordinate system， the dynamical equations with the spacecraft of massmcan be expressed as

wherer=(rx，ry，rz)Tandv=(vx，vy，vz)Tare the position and the velocity vectors of the spacecraft，respectively； the spacecraft-sun distance is expressed asr=‖ ‖r；Tmaxandαdenote the maximum thrust and the unit direction vector of the thruster，respectively.The power throttle level is denoted asu， andu∈[0，1].u=0 andu=1 mean that the thruster is in the off and fully on state.g0andμare the acceleration at ground level and the solar gravitational constant， respectively， and they take values ofg0= 9.806 65 m/s2andμ= 1.327 124 400 18 ×1011km3/s2.The specific impulse of the engine is expressed as

whereIsp-minandIsp-maxare the lower and upper limits of the specific impulse， respectively， and the specific impulseIspcan change actively.

The amplitude of thrust is obtained as

wherePmaxis the maximum input power； andηis the engine input power utilization efficiency， which varies linearly withIsp.

whereβ0andβ1are empirical coefficients of the effect of specific impulse on engine efficiency.Our work takes performance parameters of NASA’s Evolutionary Xenon Thruster （NEXT） as a reference［26］， soβ0=0.291 6 andβ1=0.962 4×10-4s-1.

In the actual spacecraft work， in order to ensure the normal operation of the system function，the electrical energy generated by the solar panel first supplies the equipment except the engine and then supplies the engine to produce the thrust.The output power of the solar panel is affected by the distance between the spacecraft and the sun， and the specific relationship is as［27］

wherePSAis the solar panel output power；PAUthe solar panel output power at 1 AU distance； the part in parentheses represents the empirical value of the solar panel efficiency changing with the instrumental day distance， whered1，…，d5are the empirical coefficients.Further， the maximum input power of the enginePmaxcan be listed［27］

wherePP-maxandPLare the maximum input power of the engine power processor and the total power required by systems other than the engine system； respectively.δis the duty cycle， which represents the power conversion efficiency.

1.2 Indirect method for low-thrust trajectory optimization

We consider a fixed-time interplanetary rendezvous problem with the performance metric of the fuel-optimal control problem

wheret0，tfandεare the departure moment， the completion rendezvous moment， and parameter of homotopy， respectively.

In order to achieve the fuel-optimal control， it is necessary to minimizeJ.The functionalJis chosen based on the work of Chi et al.［24］In their work，the decoupling of the control quantityuand the control quantity specific impulseIspis completed， which makes the problem easy to solve.The indirect method for solving OCPs introduces co-states with no specific physical meaning.Therefore， there is no clear guessing range in selecting initial values of costates， which greatly affects the efficiency of the solution.In this paper， we suggest the normalization of co-states according to the co-states normalization method in Ref.［9］.The initial values of eight costates， includingλ0， are restricted to an eight-dimensional unit hypersphere.This can narrow the guessing range and greatly improve the guessing efficiency.Since the fuel-optimal control problem is difficult to solve directly， a common approach is to introduce the homotopy parameter.First， solving the problem atε= 1.After that，εis gradually reduced from 1 to 0 using the homotopy method.Whenεis 0 corresponds to the fuel-optimal control problem.We can list the Hamiltonian function

whereλr，λvandλmdenote co-states corresponding to position， velocity， and mass， respectively.According to the Pontryagin’s minimum principle（PMP）［28］，if we want to achieve the optimal control， we need to make the Hamiltonian function take the minimum value.That isλv·αtakes the minimum value， at this timeλvandαthe direction opposite.Therefore， the optimal thrust direction is

According to the first order necessary condition we can write the Euler-Lagrange equation［24，29-30］

For Eq.（9） with the modified logarithmic homotopy function， the optimal power throttle level is written as［24］

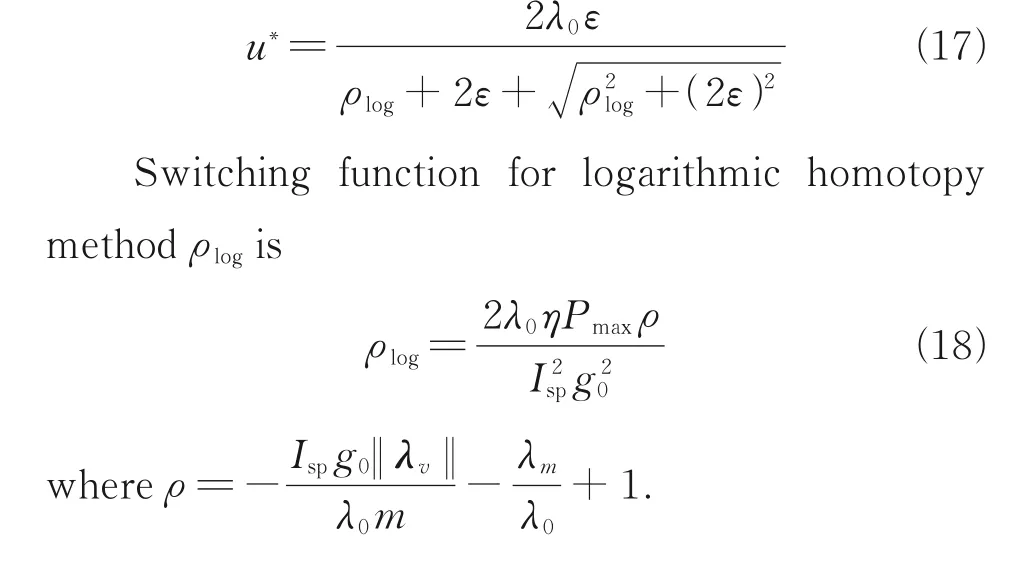
The fuel-optimal control problem is transformed into a two-point boundary value problem（TPBVP） with a spacecraft with a fixed velocity at the beginning， end positions and a fixed mission time.If the end-state mass is free， the value of the co-state at the end is zero.The shooting equation is

whererfandvfrepresent the position and the speed at the rendezvous moment， respectively， andλ=[λr，λv，λm，λ0]T.

2 Backward Generation of Fuel-Optimal Rendezvous Examples

The essence of DNNs is to construct mapping relationships between inputs and outputs， which are often complex and nonlinear.In order to obtain such complex mapping relationships， DNNs must be trained based on existing datasets consisting of a large number of samples.However， generating a large amount of sample data is extremely time-consuming.Izzo et al.［19］proposed the method of backward generation of optimal examples in their work.The idea of this method is to assume that an optimal nominal trajectory has been obtained， to perturb the variables except for the constraint of the shooting equation and to carry out the backward integration.Although the new trajectory is different from the nominal trajectory， it is still optimal because it satisfies the first-order necessary condition of optimality and does not change the shooting equation.Since the method of backward generation of optimal examples changes the TPBVP solving problem to numerical integration of trajectories， the speed of data generation is substantially improved compared to solving TPBVP directly.However， only the fuel-optimal transfer and the time-optimal rendezvous with constant acceleration have been solved［19，22］.For the fuel-optimal rendezvous control problem， the backward generation method cannot be used directly because shooting equations are different.Therefore，this paper proposes a method for backward generation of fuel-optimal rendezvous examples based on Ref.［19］.

In the shooting Eq.（19）， ‖ ‖λ(t0) -1 is the costates initial value normalization condition， which is introduced to reduce the difficulty of guessing the initial value of the co-states.However， in the backward integration from the momenttfto the momentt0， it does not need to guess the initial value of the co-states.So it is not necessary to satisfy this condition when performing the backward integration.The conditions are satisfied by the backward integral as

The position co-states， velocity co-states， and mass at the rendezvous moment are not in Eq.（20），so changing these variables has no effect on the shooting equationϕbackand does not change the optimality of the solution.We define the equation

where the superscript “ * ” indicates the value of the nominal trajectory； andδλr，δλvandδmfdenote perturbation values.The backward integration ofλr（tf），λv（tf），mfas initial conditions can obtain an optimal trajectory different from the nominal trajectory.The backward integral equation consists of the dynamical Eqs.（1—3） and the Euler-Lagrange Eqs.（12—14）.

For the rendezvous problem， there are two conditions for the backward integration cutoff.One for the initial massm*0to be reached at the integration cutoff， and the other for the integration time to be the spacecraft flight timet.When both integral cutoff conditions are satisfied， a new rendezvous optimal trajectory can be generated in backward.In this work， we use flight time as the integration cutoff condition.After that， we use the perturbedλ r（tf），λv（tf） andmfas the initial condition for the backward integration and integrate the equation to solve for the initial massm0.Then， We determine the difference betweenm0and the nominal initial massm*0， and use the idea of dichotomy to gradually and iteratively select the value ofmf.The iteration cutoff condition is

whereσdenotes the backward integration accuracy.

Now we turn the time to solve TPBVP once into the sum of multiple iterations of integration time.Trajectories solved after iteration have the same end state and different initial states as the nominal trajectory.New trajectories are still optimal since they do not change the shooting equation.The backward generation method of fuel-optimal rendezvous examples（Fig.1） is as follows：

Step 2 Set the initial mass iteration stepmstepand the iteration precisionσ.

Step 3 Backward integration withλr（tf），λv（tf）andmfas the initial value of integration； and solve the initial massm0.

Step 4 Calculate the absolute value of the difference between them0and the nominal valuem*0.If it is greater than the iteration accuracyσ， reduce the mass iteration stepmstepby half and proceed to Step 3.

Step 5 If the absolute value of the difference betweenm0and the nominal value is less than the iterative precision， the iteration ends， and the optimal trajectory is output.

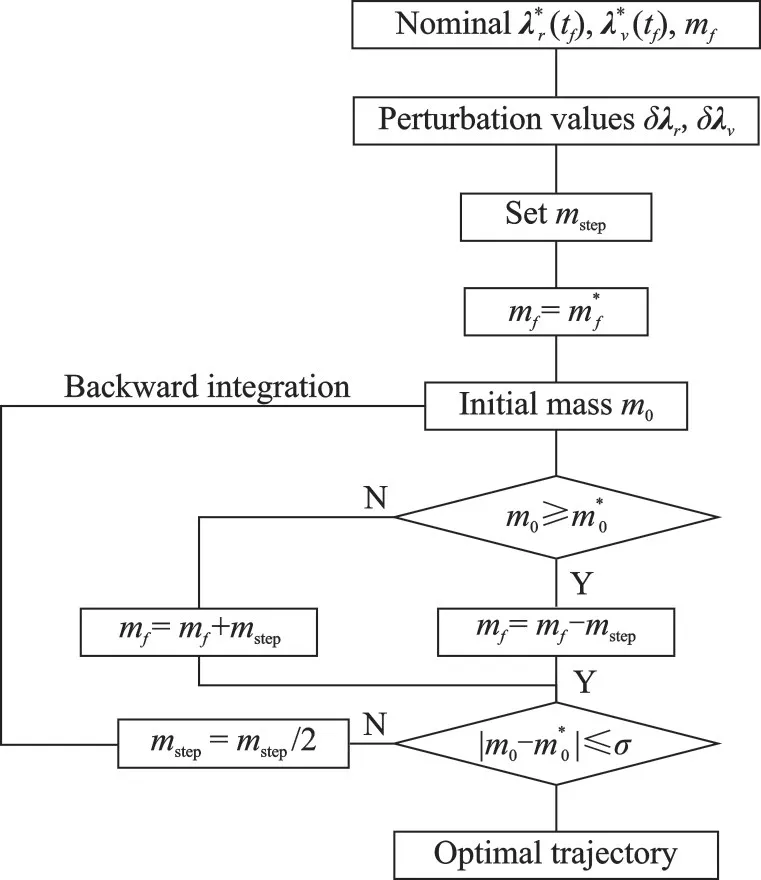
Fig.1 Algorithm for backward generation of fuel-optimal rendezvous examples

3 Deep Neural Networks for Real-Time Optimal Control

DNNs refer to the working mechanism of biological neural networks and use multiple layers and connections between multiple neurons to achieve the mapping between input and output layers.With the increase in the number of neurons and the number of hidden layers of DNNs， DNNs can theoretically achieve the mapping between any input and output.We use feedforward neural networks to learn the mapping relationship between states and control quantities of fuel-optimal control data samples.Trained DNNs can provide optimal control in real-time based on the current state information.

We use the modified equinoctial orbit elements［31］x=[p，f，g，h，k，L]Tand time as inputs to DNNs， as shown in Fig.2.The reason whyrandvin the Cartesian coordinate system （CCS） are not used as the input of DNNs is that the six-state quantities are all fast variables， and the severe data changes are not conducive to the learning of DNNs.Modified equinoctial orbit elements have only one fast variable and it differs from classical orbit elements in that modified equinoctial orbit elements are singularity-free at zero eccentricity and zero orbital inclination.Therefore， modified equinoctial orbit elements are more suitable for describing the spacecraft state.

Fig.2 Network structure

The output of the DNN is divided into two types： The thrust and the specific impulse.We use the Cartesian and orbital coordinate systems （OCS）to describe the thrust

where the thrustTCCSin the Cartesian coordinate system is represented by three componentsTx，TyandTz； the thrustTOCSin the orbital coordinate system is described by the yaw control angleα， pitch control angleβ， andμ.

For DNNs to learn the specific impulse control more accurately， we use the optimal specific impulseIsp-optof Eq.（16） as the output of DNNs.Subsequently， the actual optimal specific impulseI*spis obtained by limiting the DNN output specific impulseIsp-optusing in Eq.（15）.

The loss function measures the difference between the DNNs model and the real model.For regression problems， the mean-square error （MSE）is the most commonly used loss function.For outlier-free data， MSE is a good measure of the error between the predicted value and the true optimal value.In this paper， MSE is still used as the loss function.The reason why DNNs can accomplish very complex nonlinear mappings is the inclusion of a nonlinear activation function in the hidden layers.The choice of the activation function and other hyper-parameters are discussed in the following sections.

4 Network Training

We use Fortran to code the optimal trajectory generation program， and Python for DNN training and simulation.The positions and velocities of Earth and Mars in the example are calculated by DE421.Asteroid status information is from the Jet Propulsion Laboratory Horizons system.All simulations are implemented on a desktop computer with Intel Core i7-8700K CPU @3.70 GHz.

4.1 Nominal trajectory

Two interplanetary rendezvous missions are considered in our work： The Earth-Apophis asteroid 230 d rendezvous mission and the Earth-Mars 600 d rendezvous mission.Assume that the spacecraft in both missions use only one NEXT.According to NEXT parameters， the adjustable specific impulse range setting is as ［2 210， 4 100］s［27］.Other parameters are set asPAU=10 kW，PP-max=6.9 kW，PL=0.4 kW and duty cycleδ=0.94.The part in parenthesesd1，d2，…，d5in Eq.（7） are chosen as［32］：d1=1.106 3，d2=0.149 5，d3=-0.299 0，d4=-0.043 2 andd5=0.The specific mission information is given in Tables 1，2.

By solving Eq.（20）， we can obtain the optimal control.After that， using the homotopy method，we iterate the program and gradually reduce the value of the homotopy parameterεto finally find the fuel-optimal control.Fig.3 displays the power throttle levelufor the two missions with differentε.Whenεdecreases from 10-2to 10-6，ugradually approaches the bang-bang control.We consider the fuel-opti-mal control is achieved forε=10-6.The fuel-optimal consumption for the Earth-Apophis asteroid rendezvous mission is 128.717 8 kg， and the fuel-optimal consumption for the Earth-Mars rendezvous mission is 157.886 0 kg.

Table 1 Earth-Apophis asteroid 230 d rendezvous mission

Table 2 Earth-Mars 600 d rendezvous mission

Fig.3 Effect of homotopy parameter changes on the throttle

4.2 Database generation

We use the backward generation method of fuel-optimal rendezvous examples to generate the dataset.It is worth noting that our dataset is generated based on the two nominal trajectories described above.The mass iteration step is set asmstepand the iteration precision asσ=10-5.This parameter setting allows the initial mass of the generated trajectory to be within 0.01 g of the nominal mass.For each task， we solve the fuel-optimal control problem only once.The Earth-Apophis asteroid mission is calculated to take 28.125 s to generate 1 000 trajectories using the backward generation method and 683.766 s using the traditional homotopy method.The Earth-Mars mission takes 29.922 s to generate 1 000 trajectories using the backward generation method and 1 367.906 s using the traditional homotopy method.This shows the backward generation method of fuel-optimal rendezvous examples can greatly improve the speed of the dataset generation.

4.3 DNN optimization

4.3.1 Real-time optimal control networks

The RTOC-DNNs implement the state-control mapping.For DNNs involved in this paper， we only consider control in the spatial extent of the dataset.The dataset spatial extent refers to the maximum extent in space that can be reached theoretically when the dataset is generated.The spatial extent of the dataset depends on the extent of perturbation of the position co-statesδλrand velocity co-statesδλvin the backward generation method.We set theδλrandδλvperturbation range of the dataset for training the RTOC-DNNs at

For easy description， we refer to this range of perturbations as the 1% perturbation and also denote the following perturbation range as such.Fig.4 visualizes the range of data sets for both tasks.

Fig.4 Range of RTOC-DNNs data sets

For both missions， 10 000 trajectories are randomly selected in all training.A total of 1 001 points are taken for each trajectory at equal time intervals，for a total of 10 010 000 sample points.Where 80%of the dataset is used as the training set and 20% as the validation set.After our attempts， the activation function is hyperbolic tangent function （Tanh）， and the number of hidden layers is set to five， and each layer contains 256 neurons， which can often achieve better results.To ensure the output margin of the hyperbolic tangent activation function［33］， the range of the dataset normalization is set to ［-0.9， 0.9］.The Adam algorithm［34］is chosen as the neural network optimization algorithm， and the Adam method is very efficient in optimization because it can correct both the gradient descent direction and the learning ratelrduring the optimization process.Parameters of Adam’s method： The learning rate is set tolr= 0.001， and the parameters controlling the first-order momentum and the second-order momentum are set toβ1= 0.9，β2= 0.999.Because of the large number of training sets， we use the mini-batch gradient descent method and set the number of batches to 2 048 and the number of training sessions to 100.In addition， the optimization of neural networks using GPUs for speed.

4.3.2 Enhanced fault-tolerant networks

The RTOC-DNNs’ dataset has a small spatial distribution in the period close to the rendezvous.This creates a problem in that RTOC-DNNs barely allow for errors in the period close to rendezvous.Larger errors may cause the spacecraft to deviate from the training range of RTOC-DNNs， which in turn makes the error at rendezvous increase dramatically.To improve this situation， Izzo et al.［22］adds larger perturbed data to the dataset and make the neural network learn its control mechanism.Although this approach makes it much less likely that the spacecraft will deviate from the range of the neural network training set.However， it also increases the difficulty of neural network learning due to the introduction of larger perturbed data.For the rendezvous problem， the data set under small perturbations for the flight start moment is sufficient for neural network training， and data with larger perturbations are not needed.

In this paper， we propose the use of EFTDNNs for enhancing the control accuracy of neural networks in the second half of the flight time.EFTDNNs are independent of RTOC-DNNs， and EFTDNNs are used as a backup network to deal with the situation when the spacecraft deviates too much from the spatial extent of the training set of RTOCDNNs.For the Earth-Apophis asteroid mission， the dataset of EFT-DNNs uses a 20% perturbation.For the Earth-Mars mission， the dataset of EFTDNNs uses 8% perturbation.The spatial extent of the training data set for EFT-DNNs is shown in Fig.5.There are 10 000 randomly generated data in the dataset， and 501 feature points are selected for each trajectory at equal time intervals， for a total of 5 010 000 input and output data.Similarly， 80% of the dataset is used as the training set and 20% as the validation set.The hyper parameters settings are kept the same as those for training RTOC-DNNs.

Fig.5 Range of EFT-DNNs data sets

4.4 Network usage scheme

As shown in Fig.6， the overall scheme for the real-time control using DNNs is divided into two parts： Offline training， and online real-time control.The offline training consists of two parts： Dataset generation using the backward fuel optimal trajectory generation method and neural network.The weights and biases of each neuron in RTOC-DNNs and EFT-DNNs eventually obtained by offline training are passed to the online real-time control module.The online real-time control module inputs the real-time spacecraft status and flight time into the DNN， which outputs real-time thrust and specific impulse control.Whether RTOC-DNNs or EFTDNNs are used for control is determined by the network switching module.The network switching module switches the network depending on whether the time of flight or the spacecraft state is to exceed the DNN training space range.The DNN outputs two parts of control， thrust and specific impulse.The thrust is used directly for real-time control and the specific impulse requires truncation based on the actual specific impulse limit range for real-time control.The controlled spacecraft state is then used as input to the DNN to produce the control output.This process continues until the end of the flight.

Fig.6 DNN-based real-time control master plan

5 Numerical Results

In this section， we investigate the effect of the homotopy parameters on the training effect of DNNs.To test the effect of DNNs， we perform Monte Carlo simulations for two cases， and the number of Monte Carlo simulations is set to 1 500.Finally， the simulation results using RTOC-DNNs and EFT-DNNs are analyzed.

5.1 Exmple 1：Rendezvous from the Earth to Apophis

5.1.1 Simulation analysis in deterministic environment

One way to determine whether DNNs are better at learning the optimal control law is to investigate the size of the loss function.Table 3 shows the values of the loss function of RTOC-DNNs in two coordinate systems with different homotopy parameters.From Table 3， it can be seen that the loss function has a tendency to increase gradually as the congruence parameter decreases.This shows that the reduction of the homotopy parameter makes it more difficult for DNNs to learn the optimal control law.The smaller the homotopy parameter， the closer the control law is to bang-bang control.The bang-bang control is reflected in the sharp change of the three output thrusts in the CCS and in the OCS in the sharp change of the power throttle levelu.The bang-bang control causes a large error between the predicted and the true values of the DNN near the switch， which in turn makes the loss function increase sharply and makes it more difficult for DNNs to learn the optimal control law.But with a somewhat larger homotopy parameter， the power throttle levelubecomes more smoothly with state and flight time， the loss function is lower， and DNNs are more likely to learn the optimal control law.

Table 3 Training results (Earth-Apophis)of RTOC-DNNs

Fig.7 Monte Carlo simulation results (Earth-Apophis asteroid)

Another way to determine whether DNNs are better at learning the optimal control law is to perform Monte Carlo simulations.We perform 1 500 Monte Carlo simulations in which the departure positions of the spacecraft are randomly selected outside the training and validation sets.And the departure positions are obtained by the backward generation method with a perturbation of 1%.In this section and later simulations， the integrator uses the fourth-order Runge-Kutta algorithm （RK4） with a fixed step size， and the number of integrations is set to 1 000.The fuel consumption deviation is defined as the difference between the DNN-controlled fuel consumption and the optimal fuel consumption.Fig.7 shows the Euclidean distance， velocity， and fuel consumption deviation between the arrival state and the target state for the Monte Carlo simulations of the Earth-Apophis asteroid mission.The horizontal coordinatesAtoEcorresponds to cases with the homotopy parameterεof 10-2， 10-3， 10-4， 10-5and 10-6， respectively.For the position deviation and the velocity deviation， there is a tendency for error values to become larger asεbecome progressively smaller， and this tendency is more obvious in the OCS.For the fuel consumption deviation， caseAin both coordinate systems has the highest fuel consumption， consuming on average more than 4 kg of fuel.while theBtoEcases in both coordinate systems consume less than 0.5 kg of fuel on average.The selection of a DNN suitable for real-time control onboard requires not only making its rendezvous position and velocity deviations small， but also a comprehensive consideration of fuel consumption.We choose the network in the coordinate systemBcase with the smallest distance deviation as realtime control DNNs for this mission.The average error of distance， in this case， is 5.064 9×10-4AU， and the average error of speed is 1.075 7×10-2km/s； the average consumption is 0.350 41 kg more than the optimal fuel consumption， which is about 0.272 2% of the optimal fuel consumption.

5.1.2 Simulation analysis in uncertain environment

As the above mentioned， simulations are performed in a deterministic environment， while there are various uncertainties in the real flight environment［20］， so we further investigate the performance of DNNs in a state-uncertain environment.It is worth noting that the dataset used for DNNs training in this paper does not consider the uncertain environment.So when considering uncertainty， theoretically DNNs do not make the position and velocity errors of end rendezvous less， and often all produce larger errors than they in a deterministic environment.Although EFT-DNNs are used to compensate for the spacecraft being out of the training range of RTOC-DNNs， EFT-DNNs will not stay out of the network training range in the case of large errors， ensuring the accuracy of the control.

We simulate both cases without and with EFTDNNs.Not using EFT-DNNs means that RTOCDNNs are used throughout the mission.For the Earth-Apophis asteroid mission， we use EFTDNNs case and set the flight time from 0 to 130 d use of RTOC-DNNs for control， and after 130 d we use EFT-DNNs for control.RTOC-DNNs and EFT-DNNs are selected for the Cartesian coordinate systemBcase.1 500 Monte Carlo simulations are performed in a state uncertain environment satisfying a Gaussian distributionσrx=σry=σrz=5 km，σvx=σvy=σvz=0.003 km/s.The simulation results ：The average position error is 1.107 5×10-2AU；the average speed error is 0.446 9 km/s， and the average fuel consumption error is -1.724 4 kg without EFT-DNNs； the average position error is 5.434 9×10-3AU， the average speed error is 0.112 0 km/s，and the average fuel consumption error is 1.535 0 kg with EFT-DNNs.After calculation， the percentage of position error less than 0.01 AU is 59.33% without the use of EFT-DNNs， and this percentage is increased to 89.20% with the use of EFT-DNNs.

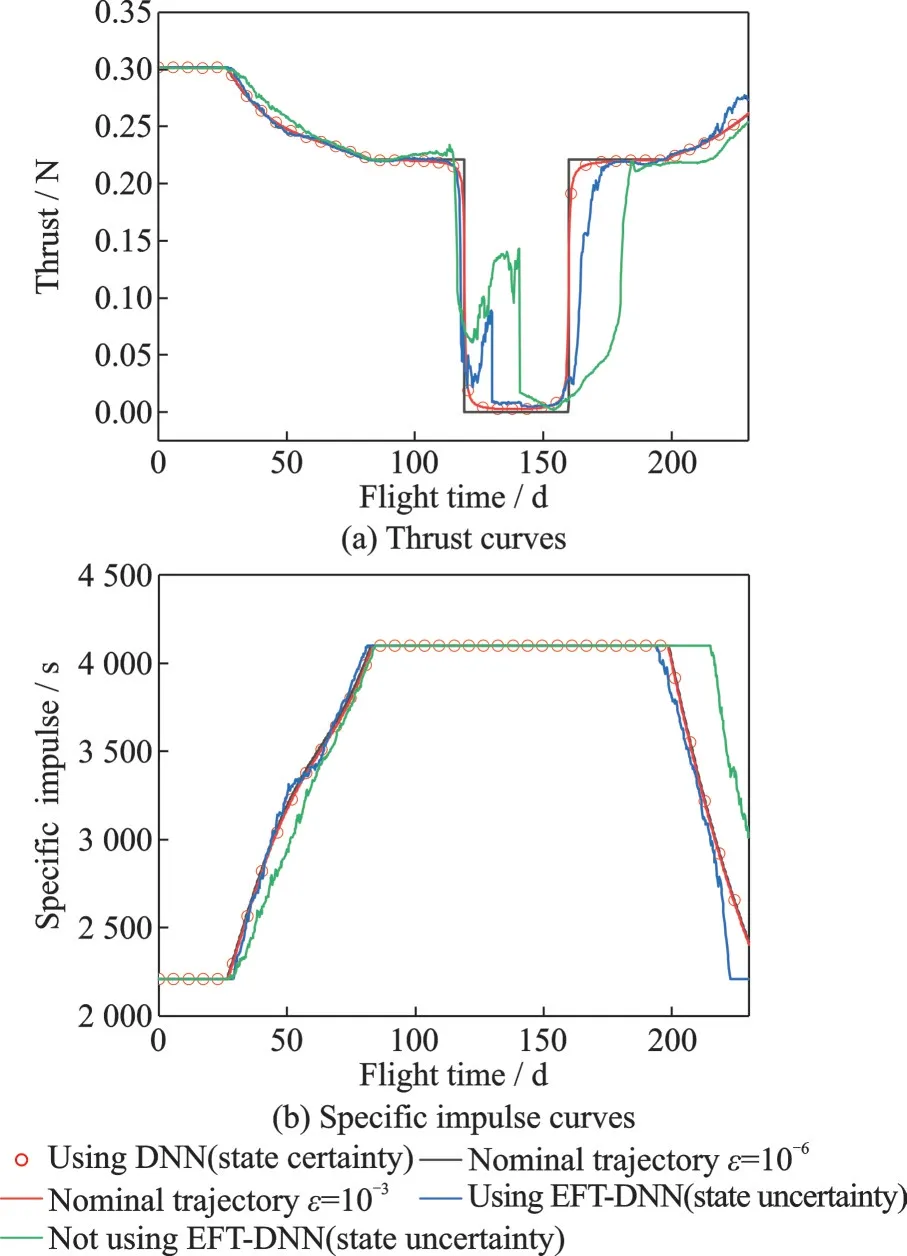
Fig.8 Variation curves of control quantities Earth-Apophis asteroid (under conditions of environmental certainty and environmental uncertainty)

Fig.8（a） shows the thrust in the deterministic environment and the thrust in the uncertain environment for the nominal departure position condition of this task， and Fig.8（b） shows the corresponding specific impulse control.First， it can be seen that the thrust and specific impulse of the DNN output in the determined environment match well whenε=10-3， indicating that RTOC-DNNs learn the optimal control well.The thrust and specific impulse curves after considering the state uncertainty are significantly different from those when the uncertainty is not considered.This also shows that the DNN outputs optimal thrust and specific impulse control based on the time and state of the current input.

5.2 Exmple 2：Rendezvous from the Earth to Mars

5.2.1 Simulation analysis in deterministic environment

We first analyze the training results （Table 4）of RTOC-DNNs.They are the same as the results of Example 1， and the loss function has a gradually increasing trend asεdecreases.This again validatesour idea that a larger homotopy parameterεwill make it easier for DNN to learn the optimal control law.

Table 4 Training results (Earth-Mars) of RTOC-DNNs

Similarly， we perform a Monte Carlo simulation with the number of simulations of 1 500.The departure position of the spacecraft in the simulation is generated by the backward generation method with 1% random perturbation.Fig.9 shows the Euclidean distance deviation， velocity deviation， and deviation relative to the optimal fuel consumption between the arrival state and the target state for the Monte Carlo simulation of the Earth-Mars mission.The meaning of the horizontal coordinate is the same as those in Example 1.Under the CCS， the average position and the velocity errors ofCare large， and those ofAare the smallest of 3.448 7×10-3AU and 5.963 7×10-2km/s.However， the deviation of fuel consumption ofAin CCS is larger，11.457 7 kg， which is about 7.256 9% of the optimal fuel consumption.In the OCS， the average position and the velocity errors tend to become larger asεbecomes smaller.The errors at the sameεare all larger than those under the corresponding CCS， so we only select the network at the output of the CCS.The deviation of the combustion consumption ofAin the CCS is too large， and the average position and the velocity errors ofCare large， both of which are not selected.The network picks among the remaining three，B，D， andE.We finally choseB，which has the smallest position and speed errors among these three.Although the fuel consumption error ofBis larger than that ofDandE， it is within the acceptable range.The average error in caseBis 4.092 2×10-3AU， and the average error in speed is 7.141 3×10-2km/s； the error in fuel consumption is 1.494 6 kg， which is about 0.946 6% of the fuel-optimal consumption.

Fig.9 Monte Carlo simulation results (Earth-Mars)

5.2.2 Simulation analysis in uncertain environment

For the Earth-Mars mission， we use EFTDNNs case and set the flight time from 0 to 350 d use of RTOC-DNNs for control， and after 350 d we use EFT-DNNs for control.RTOC-DNNs and EFT-DNNs are selected for the Cartesian coordinate systemBcondition.1 500 Monte Carlo simulations are performed in a state uncertain environment satisfying a Gaussian distributionσ rx=σ ry=σ rz=1 km，σvx=σvy=σvz=0.001 km/s.Simulation results：The average position error is 1.662 8×10-2AU，the average speed error is 0.289 2 km/s， and the average fuel consumption error of 1.342 1 kg without EFT-DNNs； the average position error is 1.040 7×10-2AU， the average speed error is 0.188 0 km/s， and the average fuel consumption error is 2.167 1 kg with EFT-DNNs.After calculation， the percentage of position error less than 0.01 AU is 38.20% without the use of EFT-DNNs， and this percentage is increased to 57.47% with the use of EFT-DNNs.Both Example 1 and Example 2 show that the use of EFT-DNNs can lead to a significant improvement in the rendezvous accuracy considering state uncertainty conditions.

Fig.10 shows the thrust in the deterministic environment and the thrust in the uncertain environment for the nominal departure position conditions of the Earth-Mars mission， and the corresponding specific impulse control is also shown.In this example， RTOC-DNNs also learns the optimal control very well.The thrust and specific impulse curves after considering the state uncertainty are more significantly different from those when the uncertainty is not considered.This is also the same as it in Example 1， which shows that DNNs tend to control the spacecraft to reach the rendezvous position optimally from the current state.

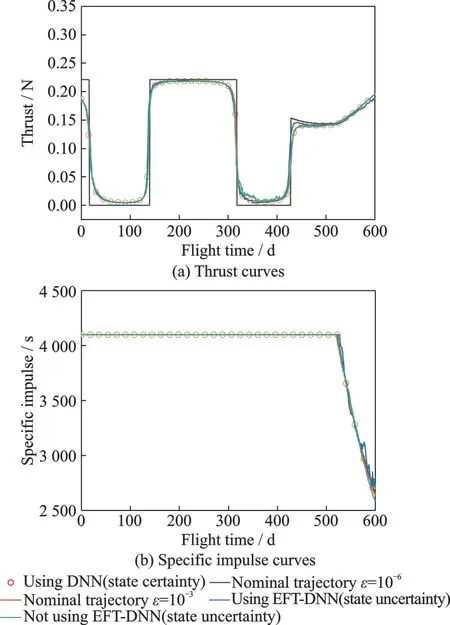
Fig.10 Variation curves of control quantities in the Earth-Mars mission (under conditions of environmental certainty and environmental uncertainty)

5.3 Network speed

The reason why DNNs are suitable for the realtime optimal control of starboard is the fast computation speed， which is shown in Table 5，for the DNNs we have chosen.The output time of the networks we use is about 0.000 23 s at a rate of 4 000 Hz or more， which proves the advantage of DNNs for real-time control onboard.

Table 5 Speed of the networks

6 Conclusions

This paper presents a method to achieve realtime optimal control of variable-specific-impulse low-thrust rendezvous via DNNs.First， the method of backward generation optimal examples for the optimal fuel rendezvous problem is proposed.The method generates datasets 24.312 times faster than the homotopy method for the Earth-Apophis asteroid mission， and 46.814 times faster for the Earth-Mars mission.Second， DNN structure is constructed for low-thrust model with variable specific impulse， and the network output control is divided into the thrust output and the specific impulse output.For the specific impulse output， a method is proposed that first learns the optimal specific impulse first and then limits it according to its actual upper and lower limits.DNNs are trained using optimal datasets with different homotopy parameters.The results show that DNNs can learn the optimal thrust and the optimal specific impulse well， and that it is more difficult for the neural network to learn the control law as the homotopy parameter decreases.After that， we conduct Monte Carlo simulations in deterministic and uncertain environments.The simulation results show that the EFT-DNNs can effectively enhance the control range in the second half of flight and improve the rendezvous accuracy.Finally， the network processing speed is calculated.The single processing time of the networks is about 0.000 23 s and the processing frequency is above 4 000 Hz， which is sufficient to show the potential of the proposed method for the real-time control onboard.