A Stochastic Modeling Method of Non-equal Diameter Pore with Optimal Distribution Function for Meso-structure of Atmospheric Ice

，，，，

1.Chengdu Fluid Dynamics Innovation Center， Chengdu 610010， P.R.China；2.Key Laboratory of Icing and De-icing Research， China Aerodynamics Research and Development Center，Mianyang 621000， P.R.China；3.State Key Laboratory of Aerodynamics， China Aerodynamics Research and Development Center， Mianyang 621000， P.R.China

Abstract: The macroscopic mechanical properties of atmospheric ice are affected by the mesoscopic pore structure，while traditional approaches to simulating still have certain limitations.To more accurately represent the mesoscopic structure of porous atmospheric ice， a new modeling method based on statistical principles is proposed.Firstly， the statistical information of atmospheric ice pore diameter is obtained by image recognition.Then， the optimal distribution function that matches the real distribution state of pore diameter is identified using a goodness-of-fit test.Next， a novel approach for deriving the geometric size of atmospheric ice models is introduced， and a method for generating random pore position and diameter data is provided.Finally， a pore intersection determination module is added to construct the mesoscopic model of atmospheric ice.The results demonstrate that the quantitative information of the pores in the generated atmospheric ice model is in good agreement with the experimental results， illustrating the accuracy and feasibility of the modeling method.Moreover， the influence of model parameters on porosity accuracy is systematically discussed.When the number of model pores reaches 50， a good balance between model accuracy and cost can be achieved.Thus， this study provides a novel method to characterize the mesoscopic features of atmospheric ice， and lays a foundation for the related simulation.

Key words：atmospheric ice； pore； meso-structure； porosity； simulation

0 Introduction

In the atmosphere， dynamic icing occurs when supercooled water droplets collide with a low-temperature surface， resulting in atmospheric ice formation.The atmospheric ice can form complex and diverse meso-structures during freezing and growth due to the fixation of air between the water film and the ice layer， as well as air bubbles in some water droplets［1］.The macroscopic view of atmospheric ice is opaque and contains numerous bubble pores in the mesoscopic view， as shown in Fig.1［2］.These pores significantly impact the macroscopic mechanical properties of atmospheric ice， such as elastic modulus， strength， density， heat transfer coefficient， etc［3-5］.Therefore， obtaining quantitative meso-structure parameters and understanding the influence mechanism of atmospheric ice pores are necessary for fundamental understanding of dynamic icing mechanisms and ice thermal/mechanical study［6-7］.

Fig.1 Thick section showing air bubbles in ice[2]

The density of ice is an important parameter for the numerical simulation of ice shape［8-10］， the mesoscopic structure of ice is closely related to the wave velocity in icing detection［11-13］， the ice pores has significant influence on the adhesion strength and thermal conductivity in the anti-icing and de-icing design［14-17］.However， most of these parameters determined by the mesoscopic structure of atmospheric ice pores are currently given by empirical setting，limiting accurate prediction of icing shape， high-precision detection of icing， and efficient design of antiicing and de-icing systems.The accurate and rapid construction of meso-structure models for atmospheric ice pores is thus crucial for the mechanical properties analysis of atmospheric ice and the design of de-icing systems.

Experimental and simulation studies have focused on the numerical simulation of nuclei formation， crystal growth， and surface contact nucleation to understand the microscopic characteristics of dynamic icing［18-19］.These studies have qualitatively shown that the meso-structure of dynamic icing is mainly affected by velocity， temperature， particle size， and liquid water content in icing conditions.The maximum pore size and porosity increase with the reduction of temperature.The air bubble volume and porosity decrease with the increasing of velocity， which can be attributed to the crushing effect of the incoming flow on the bubbles［20］.These studies show certain qualitative understanding of the microscopic characteristics of icing.However， due to the lack of detailed quantitative research， obtaining the mathematical expression and refined modeling of the meso-structure of atmospheric ice with pores under different icing conditions remains difficult.Among the prerequisites for accurate simulation of the macroscopic mechanical properties of atmospheric ice，the most critical step is to construct mesoscopic structural models of atmospheric ice with high porosity accuracy.

Representative volume element （RVE） modeling has been used to simulate the micro/mesoscopic scale structure as an effective way.The specific method is to acquire a 2-D serial image by using CT or Micro-CT， processing the image information and then reconstructing it in 3-D structure［21-22］.In the aspect of 2-D porosity analysis， the main method is to obtain the cross-section microscopic image of icing under low temperature environment， and then carry out relevant analysis［23］.However， the existing modeling methods for atmospheric ice meso-structure are not yet well developed.Li et al.［24］provided a 3-D modeling method for dynamic freezing microstructure according to the cross-section microscopic image of icing.Based on the assumption that the pores are spherical， the spherical center coordinates of the pores are randomly generated in a uniform distribution， and the diameter of the pores is randomly generated in a specified distribution.The meso-structure model of ice is generated in a given three-dimensional region by combining the position of the spherical center and the pore diameter.This method can construct the mesoscopic structure of atmospheric ice pores， but there are still some shortcomings in accuracy and operability.Firstly， the specified pore diameter distribution function leads to a weak generalization capability.Secondly， it cannot avoid the rounding error caused by the calculation of pore number in the model.Thirdly， it cannot avoid the intersection of pores-pores and pores-interfaces， which will be detrimental to the construction of high-quality meshes for subsequent finite element analysis.

In order to address the limitations of atmospheric ice meso-structure modelling technology， this study proposes a new stochastic modeling method for generating non-specified probability distribution function to characterize pore parameters.In addition，innovative techniques such as the determination of model characteristic edge lengths and pore interference intersection judgement are used to further increase the model’s accuracy.Moreover， the influence of model parameters on porosity accuracy and the balance between modeling cost and accuracy are discussed.This study aims to provide a new approach for the refined modeling of the meso-structure of atmospheric ice with pores， and to make the modeling parameter reference for the numerical simulation of the mechanical properties of atmospheric ice.

1 Stochastic Modeling Method

The modeling process for the meso-structure of atmospheric ice is presented in Fig.2， where microscopic image technology is utilized to obtain the meso-structure parameters of atmospheric ice pores.Numerical models of atmospheric ice mesoscopic structure， matching the real porosity， pore diameter size， and distribution law， are constructed through a statistical fitting method and pore numerical generation algorithm.

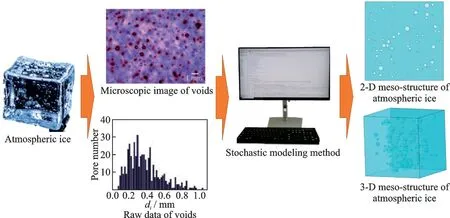
Fig.2 Schematic diagram of atmospheric ice modeling process

The statistical fitting method and pore generation algorithm of atmospheric ice pores are key to the construction of high-accuracy meso-structure models of atmospheric ice with pores.In this paper，a new stochastic modeling method is proposed to make the atmospheric ice modeling process more efficient and accurate.The specific core steps of the modeling approach are shown in Fig.3（a）， which comprise four steps： （1） Obtaining raw data of pores from images， （2） obtaining the optimal distribution function of the atmospheric ice pore， （3） calculating the meso-structure model side length， and（4） generating the meso-structure model（including generating pore center location， pore diameters，and determining the intersection of pores）.

1.1 Obtaining raw data of pores from images

Icing experiments were conducted in a 0.3 m ×0.2 m icing wind tunnel of China Aerodynamic Research and Development Center.The icing microscopic images were obtained using an Olympus CX31 microscope.The specific steps included slicing atmospheric ice in a low-temperature environment， acquiring microscopic 2-D images using a microscope， and then using image segmentation to obtain the pore sections.The perimeter and area of each pore were obtained using Matlab’s own command.Assuming the pore to be spherical， its diameter was obtained.Finally， sample data of pore diameter were counted， and the porosity and the histogram of pore diameter were derived.

1.2 Obtaining optimal distribution function of atmospheric ice pore

After obtaining the pore statistics， the optimal distribution function that best matched the true distribution of pore diameters in atmospheric ice was selected from a variety of common distribution functions.Specifically， based on the obtained pore diameter distribution data and histogram， the maximum likelihood method was used to estimate the parameters of each common distribution function.Then，based on the principle of the goodness of fit test， the sum of squared errors（ndiis the number of atmospheric ice samples，diandd̂iare the measured value and the fitted value of the pore diameter of theith sample， respectively）is used as the goodness of fit parameter.The goodness of fit parameter values of each common distribution function were calculated， respectively.Finally， the calculation results of the goodness of fit parameters were sorted， and the common distribution function with the minimum goodness of fit parameters was selected as the optimal distribution function of the atmospheric ice pore diameterF(x).

Fig.3 Modeling methods for meso-structure of atmospheric ice with pores

1.3 Calculating meso-structure model side length

After obtaining the optimal distribution functionF(x) of pore diameter， the geometric size of the meso-structure model should be derived to ensure that the porosity and pore distribution of the model are consistent with the actual situation of atmospheric ice.

When desired to construct a 3-D structural atmospheric ice model， the model feature edge lengths are determined according to the following equation

whereL3-Dis the edge length of the 3-D model，λthe porosity，F-1(1) the value of the inverse of the optimal distribution function taken at 1，F′(x) the probability density function of the optimal distribution function，xthe pore diameter， andN3-Dthe pore number in the 3-D model.λ，F-1(1)， andF′(x) are obtained from relevant steps in Sections

1.1 and 1.2.N3-D is self-determined.

When desired to construct a 2-D structural atmospheric ice model， the model feature edge lengths are determined according to the following equation

whereL2-Dis the edge length of the 2-D model， andN2-Dthe pore number in the 2-D model.

According to the above equations， the side length of the model can be accurately calculated， so as to ensure the high consistency between the porosity of the model and the real porosity of atmospheric ice.

1.4 Generating meso-structure model

The process of generating a mesoscale model is divided into three steps after obtaining the optimal distribution function and key parameters such as pore diameter， porosity， and the model’s side length.Firstly， the pore center location is generated， followed by the generation of pore diameters and the determination of pore intersection.

1.4.1 Generating pore center location

To ensure that the subsequent finite element analysis yields high-quality， uniform meshes at the boundary of the model， the generation space range of the pore center is appropriately limited， taking into account the influence of pore intersection and boundaries.Using the space corresponding to the model feature edge lengths as the model reference boundary， the pore center coordinatesOj，3-D(Xj，Yj，Zj) are generated in a uniformly random manner in theδL3-D×δL3-D×δL3-Drestricted space （δis the restricted scaling factor and the restricted space of the 2-D model isδL2-D×δL2-D）.

1.4.2 Generating pore diameters

Once the pore center coordinates are generated，the pore diameterdj，3-Dcorresponding to each pore center coordinateOj，3-D(Xj，Yj，Zj) is determined based on the random form of the optimal distribution function of atmospheric ice pore diameterF（x）.

At this point， all the geometric features of the atmospheric ice meso-structure model are generated.

1.4.3 Determining intersection of pores

The self-intersection between pores may result in a shorter mesh size at the intersection， leading to low computational efficiency in the subsequent finite element model.To improve the quality of the model， an adjacent pore intersection judgment module is added.If the distance between the center of adjacent pores is less than the sum of the radius of adjacent pores， it is determined that there is an intersection between adjacent pores.The center coordinates of each pore and the corresponding pore diameter in the model are then regenerated until all pores in the model do not intersect.This process yields the final mesoscale model of atmospheric ice.

1.5 Differences from traditional methods

In this study， the proposed method for generating meso-structure models of atmospheric ice presents several improvements and innovations compared with traditional methods.

（1）The method for generating pore diameters is improved by using the optimal distribution function instead of a specified pore diameter distribution function.Traditional methods rely on specific distribution functions to fit pore diameter distributions，which suffer from weak generalization and unclear physical meaning.For example， the pore distribution function specified in Ref.［23］ is

wherex∈［ 0， + ∞）， andk1，k2are parameters to be fitted.The proposed method in this study uses a non-parametric test based on goodness of fit to select the optimal distribution function among dozens of common distribution functions， which avoids singularity and specificity and is suitable for fitting pore diameter distributions of atmospheric ice under different conditions.

（2）The method for determining the geometric size of the model is improved by changing the calculation from pore number to model side length.Traditional methods calculate the pore number by giving model side length， which can produce rounding errors and deviate from the theoretical value， leading to differences between the model porosity and the actual porosity.The proposed method calculates the model side length， avoiding the rounding error.

（3）The proposed method considers the influence of the model boundary conditions when generating the pore center position， whereas traditional methods do not.The proposed method limits the generation space range when generating the pore center position， considering the influence of the intersection of pores and boundaries， which can generate high-quality uniform meshes at the boundary of the model for subsequent finite element analysis and avoid cutting off pores at the boundary of the model.

（4）The traditional method does not include pore intersection determination.The proposed method adds an adjacent pore intersection judgment module to improve the model’s quality， which avoids generating too small-sized meshes and causing distortion during finite element calculation.

2 Simulation

2.1 Modeling method validation

To validate the modeling method presented in this paper， atmospheric ice generated in a wind tunnel was used as an example to construct corresponding 3-D/2-D meso-structure models.The experimental state including liquid water content LWC =0.75 g/m3， mean volume diameter MVD=38 μm，wind speedv=25 m/s and temperatureT=-6 ℃.According to statistics， the porosity of the atmospheric ice is 0.051 2［24］， and the pore diameter histogram is shown in Fig.4.The Pycharm 2022.2.2 program was used to develop the models.The computer configuration was a 16-core CPU 2.2 GHz with 16 GB memory.

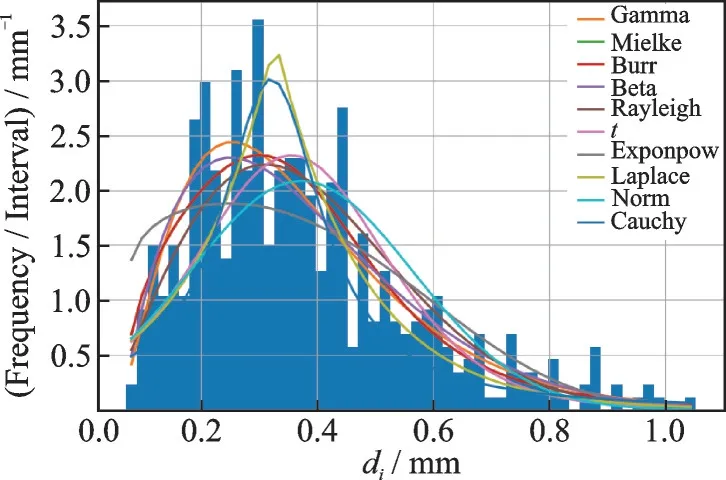
Fig.4 Void diameter histogram and distribution function fitting

The examined pore diameter distribution functions includedt， Exponpow， Laplace， Norm， Cauchy， Gamma， Mielke， Burr， Beta， Rayleigh， and other common distribution functions.The fitting results of the pore diameter distribution are presented in Fig.4.The sum of squared errors was selected to test the goodness of fit of the above common distribution function.The calculation results of the square error sum （goodness of fit parameter） of each distribution function are shown in Table 1.The results indicate that the Gamma distribution function had the smallest goodness of fit parameter value.Therefore，the Gamma distribution function was selected as the optimal functionF（x） of the atmospheric ice pore diameter.It should be noted that adding more distribution functions for examination can lead to obtaining the global optimal distribution function.

The pore number in the model was specified as 100.The side length of the 3-D model and 2-D model were determined to be 4.35 mm and 14.81 mm，respectively， based on Eqs.（1，2）.The limited scale coefficientδwas set at 0.8， and the coordinates of each pore center were randomly generated in the limited geometric space.Based on the optimal distribution function， the pore diameters were randomly generated.Intersection judgments were madeon adjacent pores to ensure that all pores in the final models did not intersect.

Table 1 Distribution function fitting degree sorting

The meso-structure modeling results of atmospheric ice with pores are presented in Fig.5， where Fig.5（a） shows the 3-D structure modeling results，and Fig.5（b） shows the 2-D structure modeling results.It can be seen that the pore distribution of the atmospheric ice model is in good agreement with the experimental observation results， as manifested in pore size， distribution， and randomness.The porosity of the atmospheric ice model was verified by calculation to be 0.051 1 （3-D model） and 0.051 4（2-D model）， consistent with the porosity value obtained from the atmospheric ice experiment（0.051 2）.Thus， the model developed in this paper has high accuracy and can accurately reflect the porosity and pore distribution characteristics of atmospheric ice.

Fig.5 Meso-structure models of atmospheric ice

2.2 Mesh generation results

To demonstrate the effectiveness of the established atmospheric ice model in obtaining high-quality finite element meshes， the model was imported into the general finite element analysis software platform ABAQUS.The results of finite element mesh generation of the 3-D structure and 2-D structure were presented in Fig.6 and Fig.7， respectively.

Fig.6 Meshing of 3-D meso-structure models of atmospheric ice

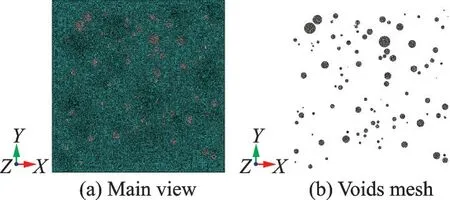
Fig.7 Meshing of 2-D meso-structure models of atmospheric ice

The generated mesh size was generally uniform， and the mesh quality was high.Furthermore，due to the avoidance of pore truncation by the model boundary， the mesh at the model boundary was uniform and symmetrical， which facilitated the application of symmetrical and periodic boundary conditions for more objective and accurate calculation and analysis of the mechanical properties of atmospheric ice.

2.3 Influences of parameter

The performance of the model is directly affected by its parameters， and therefore requires further discussion.Among the important atmospheric ice characteristic parameters， porosity stands out as a key parameter.As the porosity of the model may differ from the actual porosity obtained from experiments， this section aims to investigate the influence of model parameters on the accuracy of porosity for both the 3-D and 2-D models.Specifically， this section presents the relationship between the model porosity and the model pore number， as well as the modeling accuracy and costs.

2.3.1 Influence of model pore number on 3-D model porosity generation

To investigate the actual porosity of the atmospheric ice 3-D model， with a real porosity of 0.051 2 obtained from atmospheric ice experiment as input，the porosity of the atmospheric ice 3-D model was studied when the number of model pores was 10，50， 100， 150， and 300， respectively.A corresponding relationship exists between the model side length and the pore number， with the model side length of the 3-D model corresponding to 2.01，3.45， 4.35， 4.98， and 6.27 mm， respectively， according to Eq.（1）.To ensure repeatability， one hundred modeling experiments were conducted in each group with the same input conditions.The mean and standard deviation of the porosity of each group of models are shown in Fig.8.

The actual porosity calculation results in Fig.8 demonstrate that the mean value of the model porosity is 0.048 3 when the model pore number is 10，which is somewhat different from the true porosity of 0.051 2.However， when the model pore number gradually increases， the mean value of the 3-D model porosity gets closer to the true porosity of 0.051 2，indicating that the accuracy of porosity generation increases significantly.Moreover， the standard deviation of the model porosity tends to decrease as the model pore number increases， indicating that the dispersion of the model-generated results decreases as the pore number increases.

Fig.8 Results of 3-D model porosity generation corresponding to different model pore numbers

2.3.2 Influence of model pore number on the 2-D model porosity generation

The real porosity of 0.051 2 obtained from the atmospheric ice experiment is still used as input.The porosity of the 2-D meso-structure model of atmospheric ice is examined for different model pore numbers， namely 10， 50， 100， 150， and 300.Based on Eq.（2）， the corresponding model side lengths for these pore numbers are 4.68， 10.47，14.81， 18.14， and 25.66 mm， respectively.One hundred modeling repeatability experiments were carried out for each group of 2-D models， with all input conditions held constant.Fig.9 shows the mean values and standard deviations of porosity for each group of models.

Fig.9 Results of 2-D model porosity generation corresponding to different model pore numbers

From the actual porosity generation results of the 2-D models in Fig.9， it can be observed that when the model pore number is small （N=10）， the porosity of the model is 0.048， which differs significantly from the real porosity of 0.051 2.As the model pore number increases to a certain point （N≥50），the porosity of the model becomes very close to the real porosity of 0.051 2， ranging from 0.051 0 to 0.051 6.Furthermore， as the model pore number increases， the standard deviation of the porosity of the 2-D model decreases.Additionally， compared to the generation results of the 3-D models， the porosity dispersion of the 2-D model is smaller under the same model pore number.

2.3.3 Modeling accuracy and cost

In regards to the modeling accuracy and cost，it was observed that the porosity accuracy of both 3-D and 2-D models increased as the number of model pores increased within a certain range.Specifically， when the number of pores in the model reached 50 or more， the average porosity of the model closely aligned with the real porosity of 0.051 2， as demonstrated in Fig.10.

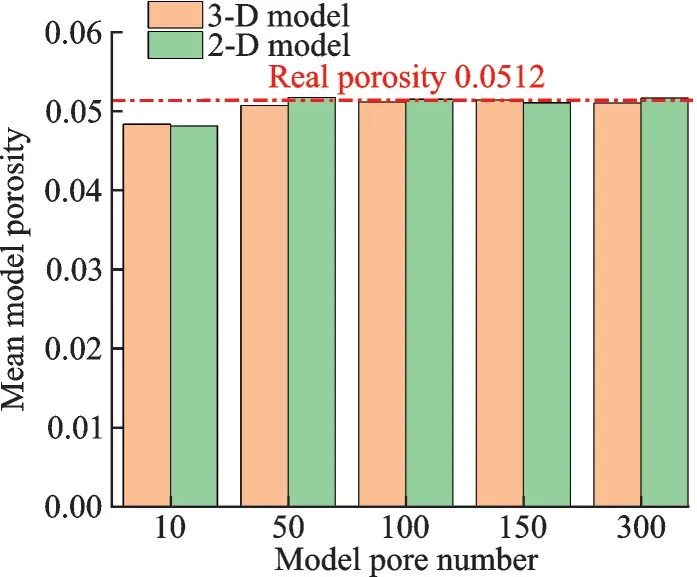
Fig.10 Mean model porosity of 3-D model and 2-D model corresponding to different model pore numbers

In contrast to the literature method， which necessitates a model pore number of 1 000 for comparable accuracy of the model porosity［24］， the proposed method only requires 50 pores to achieve similar precision.This suggests that our method is more accurate and convenient， and capable of modeling the meso-structure of atmospheric ice with high porosity accuracy at a lower modeling cost.

Furthermore， an increase in the model pore number leads to an increase in modeling costs， as well as subsequent model meshing and solution time.To minimize the modeling cost， it is advisable to reduce the model pore number and geometry size while maintaining high porosity accuracy.As Table 2 illustrates， when the pore number in the model is 50， the modeling time is approximately the 1/40th of the time required for 1 000 pores.In comparison to the literature method， the proposed method significantly reduces the required modeling time while sustaining equivalent porosity accuracy.Additionally， both the modeling time and the model finite element solution time are directly proportional to the pore number and the size of the model.Thus， this modeling approach presents notable advantages in minimizing the computational cost of batch and parametric atmospheric ice mechanics analysis， which can enhance the efficiency of icing and anti-icing research and design.

Table 2 Model generation time corresponding to different model pore number

3 Conclusions

A novel stochastic modelling method for nonequal diameter pores with an optimal distribution function has been proposed to construct a refined meso-structure of atmospheric ice and acquire quantitative meso-structure parameters.The proposed method can provide a technological foundation for simulating and investigating the mechanical properties of atmospheric ice， considerably increasing modelling accuracy， quality， and efficiency.Specific conclusions and innovations of this study are described below.

（1） The optimal distribution function that strongly matches the actual pore diameter distribution of atmospheric ice can be automatically filtered based on the goodness of fit test method.This avoids the weak generalization ability and severe limitation of traditional specified distribution function methods.

（2） The model’s geometry is determined using the computation of model side length， rather than the calculation of pore number.This can increase modelling accuracy by preventing rounding mistakes in pore number computation.

（3） Corresponding algorithms are designed to avoid the drawbacks caused by the intersection of pores-pores and pores-interfaces.This enables obtaining a high-quality finite element mesh for the created model and the implementation of periodic boundary conditions on the boundary surfaces.

（4） The study examines the balance between modelling cost and accuracy， along with the impact of model pore number on the actual porosity of 3-D and 2-D models.Results reveal that once the pore number reaches 50 for both 3-D and 2-D models， the model porosity is extremely compatible with the actual porosity， and the model modelling costs are much lower than using conventional techniques.Thus， it is recommended to adjust the pore number to at least 50 in atmospheric ice meso-structure modelling.

Subsequent work will focus on collecting， modelling， and experimenting on atmospheric ice samples under different icing conditions.The ultimate goal is to obtain a mapping between “icing conditions-meso-structure of atmospheric ice-atmospheric ice mechanical properties”.