面向泊位共享的泊位资源预测与分配模型

郑圣旺,王京元,高颖超

(1.浙江省交通运输科学研究院,杭州 310023;2.深圳大学 土木与交通工程学院,广东 深圳 518060;3.潍坊学院 数学与信息科学学院,山东 潍坊 261061)

在城市“停车难”背景下,泊位共享伴随着共享经济的浪潮应运而生。泊位共享是指将某一停车场非高峰时段的闲置泊位为周边有停车需求的对象提供停车服务[1-2]。随着泊位共享理论的共识化推广,共享泊位资源的预测与分配作为有重要意义的研究课题,近年来受到了国内外学者的广泛关注,并展开了持续研究。

相关研究可分为共享泊位的预测和分配两方面。在共享泊位资源预测方面,现有研究大多基于一种理论方法建立单一的预测模型:Dunning[3]构建基于自回归移动平均理论的泊位占用预测模型;Caliskan等[4]构建基于齐次马尔可夫算法的空余泊位预测模型;刘志广[5]、陈恺[6]构建基于时间序列分析方法的泊位共享时间窗预测模型。由于单一预测模型考虑因素有限,从预测结果看,精度有待提高。在共享泊位资源分配方面:姚恩建等[7]以提高泊位资源利用率为目标,研究住宅区业主自主上报的车位空闲时段与停车请求时段匹配模型;唐秋生等[8]为提高居住区泊位利用率,构建一种错时错位泊位共享匹配模型;Xie等[9]将结构方程模型和Logit模型相结合,构建泊位动态分配模型;CAI等[10]以拒绝停车请求最少、共享收益和泊位利用率最大为目标建立两阶段泊位分配方法;Shao等[11]、张水潮等[12]从停车运营管理方出发,以运营企业收益最大化为目标,基于0～1线性规划理论构建共享泊位与停车需求者间的泊位分配模型。上述研究均是在全局信息已知情况下构建的车位级固定泊位分配模型[13-16]。由于固定泊位分配模型要将停车需求分配到具体泊位,因此需要知道每个泊位的空闲时间,要求泊位所有者自主如实的上报泊位空闲时间,由于泊位所有者共享意愿影响因素较多[17],上报的泊位空闲时长不确定性较大。而在实际运营中,停车场多为有车位即可停的随机泊位模式,且收费模式会影响驾驶人对停车场的选择和泊位分配结果。

鉴于此,文中提出一种基于共享泊位供给量预测的泊位分配模型,先建立基于停车历史数据的泊位供给量组合预测模型,进而构建不同收费模式下的共享泊位分配模型。理论上,该方法无需依赖泊位拥有者上报的泊位空闲时间,仅利用共享停车场历史停车数据即可实现对共享泊位供给量的预测,且能改善既有研究单一理论模型预测精度不高的问题;在应用中,该模型与停车场实际运营结合更为紧密,且停车场历史车辆进出数据较易获得,更具实践性。

1 共享泊位供给预测

1.1 建模机理分析

停车场供给共享泊位即空余泊位,是指给定时段(统计周期)内自始至终均未被占用的泊位数。其短期变化为非平稳非线性,影响因素较多且难以用函数量化,但长期来看,变化趋势呈现出一定规律性,每个时段的空余泊位数与历史数据存在某种相关性[18]。研究表明,BP神经网络对于具有非线性、难量化等特征的时间序列问题预测具有较好的适用性[19],因此,文中基于BP神经网络构建共享泊位供给组合预测模型。

1.2 关键参数确定

综合考虑预测效果、模型复杂度和网络学习时间[20],文中采用单隐藏层BP神经网络。根据网络结构,结合空余泊位预测特点和已有研究成果[21],确定网络主要参数取值。

1.2.1 输入层神经元个数

采用皮尔逊相关系数r进行相关性判断,r的绝对值越接近1,表明两个数据序列相关性越强;r的绝对值越接近0,表明两个数据序列相关性越弱[22]。选取深圳市前海鲤鱼门西街停车场2020年9月21日至9月25日的5个工作日空余泊位统计数据,计算所预测时段空余泊位与前m个相邻时段空余泊位之间的相关性。初选m=10,即计算所预测时段与前10个相邻时段的相关性大小,结果表明:随着时间序列的前移,相关性呈逐渐下降趋势。以r=0.9作为选取临界值,由表1可知,当m=5时r≥0.9,故输入层的神经元个数选取为5,即以预测时段的前5个相邻时段空余泊位数作为预测输入数据。

表1 相关系数r计算结果

1.2.2 输出层神经元个数

文中预测对象为停车场未来某时段的空余泊位数,故输出层神经元个数为1。

1.2.3 隐藏层神经元个数

采用试验法确定隐藏层神经元个数:首先从少量神经元开始训练,再逐个增加神经元个数,对比不同神经元个数下的预测误差,误差最小的即为符合试验要求的隐藏层神经元个数。试验结果表明(见表2),当隐藏层神经元个数为8时预测效果最好,故隐藏层神经元个数确定为8。

表2 隐藏层神经元个数实验结果

1.2.4 激活函数

BP神经网络需要确定隐藏层和输出层两个激活函数。根据文献[18]所述,隐藏层的激活函数选用Sigmoid非线性函数,输出层的激活函数根据实际预测问题来选择。文中预测对象为停车场未来某时段的空余泊位数,属于回归预测问题,回归预测问题是根据输入数据预测一个连续数值,选用Purelin线性函数。

1.2.5 学习速率

根据文献[21]所述,学习速率用来调节神经网络训练学习过程中参数调整的快慢,若每一步跨越太大,就会失去曲线很多变化信息,学习速率过小,网络训练速度也会较慢,文中取学习速率为0.01。

另外,最大训练次数取10 000次,最小设定误差取0.000 1。

1.3 预测模型构建

基于BP神经网络,将历史数据作为先验条件对未来时段空余泊位数进行预测,但先验数据时间粒度的选取会直接影响预测结果的精确度[23]。为具有对比性,分别采用当日相邻时刻、相邻工作日同时刻、相邻周同工作日同时刻等不同时间粒度对输入层样本数据进行处理,构建3种不同时间粒度下的预测模型,并基于3种预测结果进一步构建组合预测模型,以提高预测精度。

1.3.1 当日相邻时刻预测模型

基于当前时刻以及与其相邻的前4个时刻空余泊位,预测未来相邻时刻空余泊位。如图1所示,设当前时刻为Tn,n表示时刻,当前时刻有效泊位数量为Xn,则Xn+1为对应Tn时刻所预测的期望输出值。

图1 当日相邻时刻预测模型

1.3.2 相邻工作日同时刻预测模型

基于当前工作日的当前时刻,以及与其相邻的前4个工作日在相同时刻的空余泊位,预测未来相邻工作日在相同时刻的空余泊位。如图2所示,设当前时刻为Tn,m表示周工作日(weekday),n表示时刻,对应的有效泊位数量为Xmn,则X(m+1)n为对应Tn时刻所预测的期望输出值。

图2 相邻工作日同时刻预测模型

1.3.3 相邻周同工作日同时刻预测模型

基于当前周的当前工作日当前时刻,以及与其相邻的4个周在相同工作日、相同时刻的空余泊位,预测未来相邻周在相同工作日、相同时刻的空余泊位。如图3所示,设当前时刻为Tn,k表示周,m表示周工作日(weekday),n表示时刻,对应的有效泊位数量为Xkmn,则X(k+1)mn为对应Tn时刻所预测的期望输出值。

1.3.4 组合预测模型

组合预测模型基本思想是把各单一模型预测结果进行加权组合,得到一个更加准确的预测结果[24],如图4所示。

图4 组合预测模型

以误差平方和最小原则确定各单一预测模型权值。记Q为组合模型预测误差平方和,则可建立以下模型,最终可求得各单一预测模型权值分配结果。

(1)

(2)

式中:xt为所要预测的目标对象第t时刻的真实值;zt为组合模型第t时刻预测值;et为组合预测模型第t时刻预测误差;m为单一预测模型个数;wi为第i种单一预测模型在组合模型中所占的权重。

1.4 实证分析

1.4.1 数据来源

以深圳前海鲤鱼门西街停车场2020年9月24日08:00—20:00时段内空余泊位预测为例,通过前海停车管理云平台获取鲤鱼门西街停车场2020年8—9月的车辆进出时间序列数据,并以15 min为统计周期,统计各时段空余泊位数量。

1.4.2 预测流程

基于BP神经网络和组合预测理论的停车场空余泊位预测流程如图5所示。

图5 基于BP神经网络和组合预测理论的空余泊位预测流程

1.4.3 仿真实验

采用前述3种基于BP神经网络算法的预测模型处理样本数据;再分别将设定好的BP神经网络参数代入到预测流程进行仿真实验,分别得到3种单一预测模型的预测结果;最后,将3种预测结果代入到组合预测模型,求得3种单一预测模型的最优权值分别为0.077 3、0.089 1和0.833 6,进一步得到组合预测模型预测结果。具体预测结果如图6～7所示。

图6 4种预测模型预测结果与实际值对比

图7 4种预测模型预测结果相对误差

1.4.4 结果分析

采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)3个预测误差评价指标,比较4种模型的预测效果,计算结果如表3所示。

表3 4种模型预测结果评价

上述对比结果表明:就3种基于BP神经网络算法的单一预测模型来说,相邻周同工作日同时刻模型的性能指标评价值均为最低,预测效果最好,反映了人们在不同周的相同工作日具有比较相似的出行特征;而组合预测模型,使得3个性能评价指标均得到了一定程度的改善,预测效果相对最好。综合各单一预测模型的组合预测模型在一定程度上能更加全面地反映数据变化信息,有效预测停车场下一时刻的泊位变化趋势。

2 共享泊位分配模型

区别于既有泊位分配模型研究“共享泊位供给数据全局已知”的假定,文中所构建分配模型的供给数据基于前述预测模型得出,且将收益管理思想引入分配过程,分别构建固定收费和阶梯收费模式下的共享泊位分配模型。

2.1 问题描述

假设在夜间停车矛盾突出的某居住区,存在步行距离在可接受范围的某办公停车场,二者达成泊位共享意愿,居住区为共享泊位需求方,办公停车场为共享泊位供给方。

假设ts为泊位共享开始时间,te为泊位共享结束时间,则[ts,te]为共享时段,将共享时段以Δt等间隔划分为K个离散时间间隔,则第k个间隔的时间段为[ts+(k-1)Δt,ts+kΔt]。

假设居住区在时段[ts,te]内有溢出停车需求M个,为解决停车需求,每个溢出的停车需求用户m在共享平台提交停车请求。定义DM×K为共享泊位需求矩阵,表示共享平台收集的停车请求,矩阵元素dm×k表示停车用户m在k时段是否有需求,若在k时段有需求,则取值为1,否则取值为0,则有

DM×K=[dmk]M×K,m=1,2,…,M;

k=1,2,…,K

(3)

其中

dmk=

(4)

假设办公停车场在[ts,te]时段内有空余泊位用于共享,定义S1×K为共享泊位供给矩阵,表示各间隔时段可用于共享的泊位数量,矩阵元素sk为k时段所预测的空余泊位数,则有

S1×K=[sk]1×K,k=1,2,…,K

(5)

文中所构建模型的共享泊位供给数据是基于BP神经网络的组合预测模型得出。

假设停车运营管理方在泊位分配决策时段内将共享泊位需求与供给进行优化匹配,以最大共享效益为目标做出泊位分配决策。定义X1×K为共享泊位分配矩阵,表示共享泊位需求与供给的匹配结果,矩阵元素xm表示用户m的停车请求是否被接受,若被接受,则取值为1,否则取值为0,则有

X1×M=[xm]1×M,m=1,2,…,M

(6)

其中

(7)

2.2 模型构建

2.2.1 目标函数

停车场收费模式会对驾驶员的选择和泊位分配结果产生直接影响,以停车场运营方共享收益最大化为共享泊位分配模型的优化目标,总目标函数为

w=Gs-Gj-Gy

(8)

式中:w为总收益;Gs为总收入;Gj为拒绝停车请求惩罚总成本;Gy为预测误差惩罚总成本。

2.2.2 固定收费模式下的共享泊位分配模型

固定收费即每小时收费为定值,不随停车时长而变。设每小时收费为p0,停车时长不足1 h的按1 h收费,则总收入为

(9)

当供给小于需求时,部分停车请求会被拒绝,会影响被拒绝停车请求用户对共享平台的信任度,因此,需对拒绝的停车请求设置一定潜在惩罚损失,设隐形惩罚系数为μ,则有

(10)

当预测值与实际值存在误差时,可能会出现已经接受的停车请求按时到达停车场却无泊位可停情况。故针对预测误差,需设置一定的潜在惩罚损失,设隐形惩罚系数为σ,预测误差为φ,则有

(11)

综上所述,可建立以下分配模型

(12)

(13)

(14)

(15)

式(13)表示每个时间间隔接受的停车请求数不得超过该时间间隔内的共享泊位供给数;式(14)表示停车请求的预约进出场时间均需在泊位共享时间段内;式(15)表示决策变量为0～1。

2.2.3 阶梯收费模式下共享泊位分配模型

(16)

(17)

2.3 模型求解

共享泊位分配模型实质为0～1整数线性规划模型,可将其转化为以下一般矩阵形式进行求解。

max(min)w=CX

(18)

(19)

式中:约束方程系数矩阵A为共享泊位需求矩阵DM×K的转置矩阵;矩阵B为共享泊位供给矩阵X1×K的转置矩阵;目标函数系数矩阵C可根据所给条件计算得出。

2.4 指标体系

为验证分配模型在实际应用中的有效性,采用以下3种评价指标对分配结果进行评价分析。

2.4.1 共享停车总收益

记共享停车总收益为θ,为共享泊位分配模型的目标函数值,以固定收费模式为例,则有

(20)

2.4.2 停车请求接受率

记停车请求接受率为λ,为停车场所接受的停车请求数与总停车请求数的比值,则有

(21)

2.4.3 共享泊位利用率

记共享泊位利用率为τ,表示接受的停车请求占总时长与共享泊位供给总时长的比值,则有

(22)

3 数值分析

以深圳前海鲤鱼门西街停车场及其周边龙海家园居住小区为例,对共享泊位供给预测及分配结果进行分析。

3.1 实验数据

3.1.1 模型基础参数

鲤鱼门西街停车场工作日夜间19:00至次日早8:00时段泊位占用率较低,而其周边居住区刚好相反。因此,选取工作日夜间19:00至次日早8:00时段为共享泊位分配时段,以Δt=15 min为划分间隔。为使各收费模式有可比性,以停车时长为平均停车时长时3种收费模式的总收入相同为原则,确定收费规则。经调查,周边居住区夜间平均停车时长为5 h,最高可接受总停车费用为20元。固定收费模式下,取停车费为每小时4元;递减阶梯收费模式下,取首小时停车费为10元,之后每小时2.5元;递增阶梯收费模式下,取首小时停车费为2元,之后每小时4.5元。

3.1.2 共享泊位供给数据

采用基于BP神经网络的组合预测模型,对泊位共享开放时间段内各15 min间隔时段的空余泊位数进行预测,预测误差φ=0.48%,预测结果如表4所示。基于预测结果,可得共享泊位供给矩阵S1×52(限于篇幅,表4以1 h的4个时段为1行)。

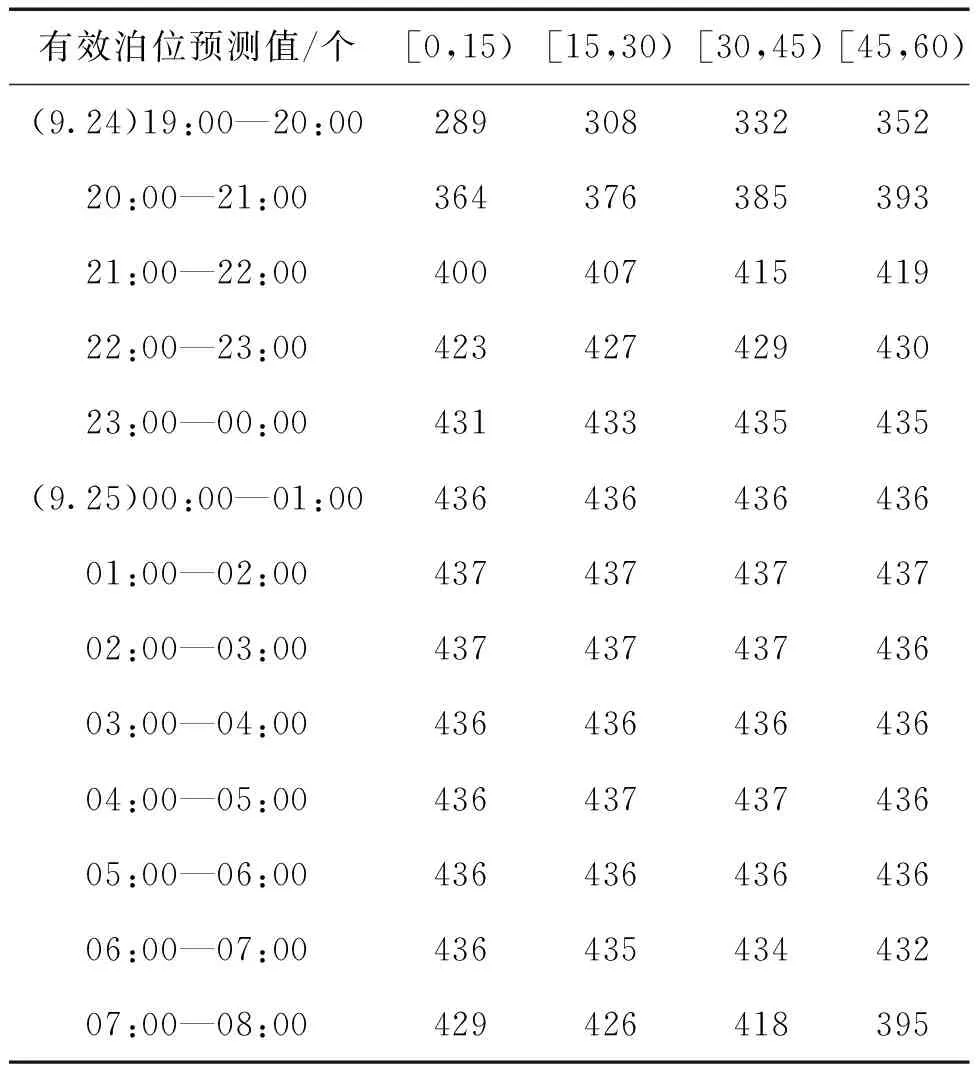
表4 基于BP神经网络的组合预测模型预测结果

3.1.3 共享泊位需求数据

将鲤鱼门西街停车场附近的龙海家园小区车辆进出数据,作为共享平台停车需求数据的备选数据集,根据数值实验(见3.2节)的测算工况需要,随机抽取共享时间段内M辆车的进出数据,将各辆车的进出时间作为其请求共享停车的起止时刻,进而计算各停车请求停放时长,得到共享泊位需求矩阵DM×K。

3.2 结果分析

采用数值实验对比分析不同收费模式下的分配效果,并结合本案例实际,确定实验输入模型的停车请求数[0,1 000]。先抽取M=20个停车共享需求作为第一个测算工况,然后按照20个的步长增加请求车辆数,在上一工况已抽取车辆基础上进行增补,抽取生成下一工况的共享泊位需求矩阵,直至M=1 000个。综合分析在停车请求数变化情况下,不同分配模型各评价指标的变化特征。

3.2.1 评价指标对比分析

图8～10分别为各分配模型的共享停车收益率、请求接受率和共享泊位利用率等评价指标变化图。根据共享停车接受率变化图,并综合收益率和利用率曲线,结合曲线形态和变化率大小,可发现存在520和620两个拐点,从而将变化过程分为3个阶段:当共享停车请求数不超过520个,停车请求接受率均为100%,可理解为空余泊位供给充足,所有请求均可被接受,即供大于求;当超过520个,停车请求接受率开始下降,当大于620个时,停车请求接受率下降加速,详细分析如下。

图8 共享停车总收益对比

图9 停车请求接受率对比

3.2.1.1 阶段一:M∈[0,520),供大于求

此阶段共享泊位供给充足,所有停车请求均可被接受,且随着被接受停车车辆数的增加,共享停车总收益和共享泊位利用率呈线性增长,直至请求数逼近供给数520个,但因供给和需求时段的匹配度问题,共享泊位利用率并未达到100%。因所有停车请求均被接受,停车收益主要由停车费率和时长决定,故递增阶梯收费模式的共享停车总收益最高,固定收费模式次之,递减阶梯收费模式最低。

3.2.1.2 阶段二:M∈[520,620),需求逼近供给、甚至略大于供给,供求相近

此阶段供给约束开始起作用,出现停车请求被拒绝现象,共享停车接受率由100%开始缓慢下降。随着停车请求数的增加,平台共享停车时段的匹配成功率提升,共享泊位利用率仍在缓慢上升。由增加的所接受的停车请求带来的收入使得总收益在这一阶段仍在增加,但受限于所拒绝的停车请求带来的惩罚成本,增长率明显放缓,当M=620个时总收益达到最高。3种收费模式的收益高低同阶段一,递增阶梯收费模式最高,递减阶梯收费模式最低。

3.2.1.3 阶段三:M∈[620,+∞),供小于求

随着停车请求的进一步增加,共享泊位利用率缓慢向100%逼近,当上升到92%后,逐渐趋于稳定,停车接近饱和,平台无法再接受新的请求。同时,拒绝的停车请求数量越来越多,停车请求接受率持续下降。与阶段二相比,由于接受的停车请求几乎没有增加,而拒绝请求的惩罚成本不断增加,蚕食停车收益,导致总收益逐渐下降。从收费模式视角看:递增阶梯模式下请求接受率最低,总收益和共享泊位利用率都最高;而递减阶梯收费模式则反之,固定收费模式均居中。

综上,随着共享停车请求数量的变化,3种收费模式下的停车请求接受率与共享泊位利用率全程均非常接近。递增阶梯收费模式的共享停车总收益始终最高,递减阶梯收费模式的共享停车总收益则最低,且呈现出“线性上升—缓慢上升—缓慢下降”三个阶段的变化趋势。

3.2.2 所接受停车请求的停车时长分布对比分析

以给定停车请求M=800个为例,对比分析3种分配模型所接受请求的停车时长分布情况,如图11所示。由图11可知,递增阶梯收费模式接受的长时停车请求最多,而递减阶梯收费模式接受的短时停车请求最多,表明在既定收费模式下,共享停车位的分配结果均为获得最大收益,与式(16)的优化目标一致。另外,这也解释了以下原因:递增阶梯收费模式的停车接受率略低,而泊位利用率却略高;递减阶梯收费模式的停车接受率略高,而泊位利用率却略低。

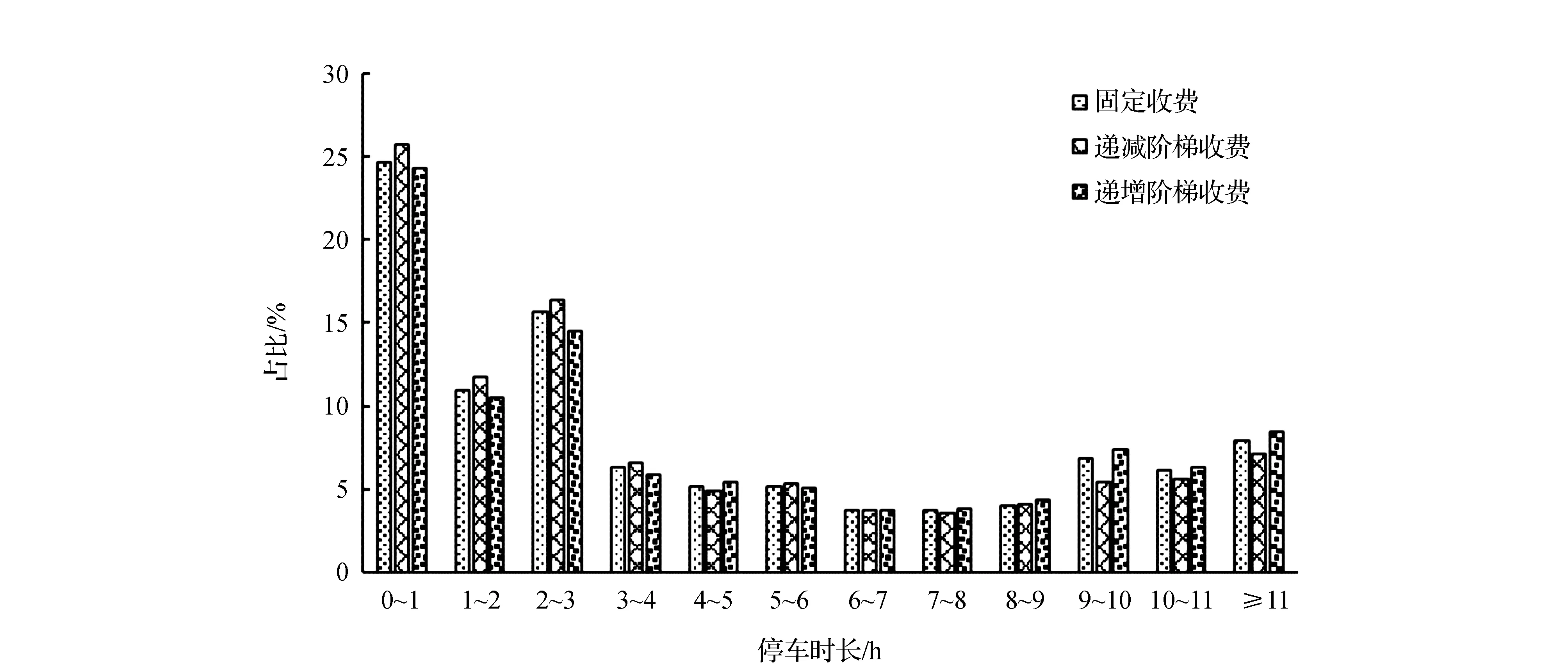
图11 3种收费模式下所接受停车请求的停车时长分布对比(M=800)

3.2.3 泊位共享实施效果分析

基于以上分析,本案例选取递增阶梯收费模式下的泊位分配模型,以给定停车请求M=800个为例,对比分析共享停车模式实施前后,停车场泊位利用率的变化情况,即不同时段停车场被占用泊位数与总泊位数的比值变化情况。从图12可看出,共享停车实施前后,泊位利用率发生显著变化,尤其是夜间,实施前低谷时仅为14%,实施后,泊位利用率显著提升,峰值达到76%。

图12 共享停车模式实施前后停车场泊位利用率对比图(M=800)

4 结 论

区别于既有研究中“共享泊位供给数据全局已知”的假定,文中将泊位预测与分配相结合,提出一种基于共享泊位供给量预测的泊位分配方法。采用基于BP神经网络的组合预测模型对停车场未来不同时段共享泊位供给量进行预测,从停车运营管理方的视角以总收益最大为目标,构建固定收费、递减阶梯收费、递增阶梯收费3种收费模式下的共享泊位分配模型。通过数值实验,从共享停车总收益、停车请求接受率、共享泊位利用率、停车时长分布、停车场泊位利用率等多方面对模型的分配效果进行分析和验证。基于本案例得到以下结论。

1)组合预测模型能有效改善单一预测模型预测效果,提升共享泊位供给量预测精度,文中案例的平均绝对百分比误差为6.49%。

2)从供需关系视角看,共享泊位利用率随停车请求数单调增加,逐渐逼近100%。停车接受率在供大于求时为100%,供需相近时开始降低,而共享停车总收益则呈现“线性上升—缓慢上升—缓慢下降”的三阶段变化趋势,在供求相近阶段的尾端达到最大值。

3)从收费模式视角看,递增收费模式的共享停车总收益一直最高,递减阶梯收费模式则反之,固定收费模式居中。停车请求接受率和共享泊位利用率在需求接近供给后开始体现出稍许差别。递增阶梯模式下,请求接受率最低,共享泊位利用率则最高,递减阶梯收费模式则反之。

4)基于共享收益最大为优化目标的分配结果表明,递增阶梯收费模式接受的长时停车请求最多,而递减阶梯收费模式接受的短时停车请求最多。递增阶梯收费模式与递减阶梯收费模式相比,停车接受率略低,而泊位利用率却略高。

5)所构建的共享泊位分配模型可显著提高整个停车场泊位利用率,在夜间共享时段,停车场泊位利用率由共享前低谷的14%提升到共享后的76%。

基于上述结论可以看出,站在停车运营管理方角度,在停车请求接受率相差不大的情况下,为追求更高效益,具有更高共享收益和泊位利用率的递增阶梯收费模式往往是首选,尤其是对于实施长时泊位共享用地类型,递减阶梯收费模式对于实施短时泊位共享的用地类型会体现出一定优势。研究成果可为共享停车场运营模式的制定和共享泊位的分配决策提供有效参考。需要指出的是本研究将共享时间段设定为连续时间段,对在实际中开放多个不连续共享时间段的停车场共享泊位分配问题可做进一步研究。