一种改进的刻画S 盒的球方法*

王永兴，冯秀涛，徐圣源

1.中国科学院 数学机械化重点实验室，北京100190

2.中国科学院大学，北京100049

1 引言

混合整数线性规划(mixed integer linear programming，MILP) 是一种寻找某个线性目标函数最大值或最小值的基础方法，其中，目标函数的变量受到一些线性约束(即这些变量满足某个不等式组).MILP 被广泛应用于运筹学、图论和计算几何等领域[1].一个MILP 问题可以有如下描述: 给定一个矩阵Rm×n，一个向量Rm以及n个实数c1，c2，···，cn，寻找一个满足Ax ≤b的Zn，使得目标函数达到最大或最小，这里m和n是两个正整数，R 和Z 分别是实数集和整数集，Rm×n、Rm和Zn分别代表R 上m×n阶矩阵集合、R 上m维向量空间以及Z 上n维向量空间.

在密码学领域，MILP 被成功应用到密码分析中.在2009 年，Borghoff首次将二元域上求解稀疏二次方程组的问题转化为一个组合优化问题，并且提出了对一些Trivium 简化版本的数值攻击[2].在2011年，Albrecht 和Cid 通过冷启动攻击得到了带噪声的非线性代数方程组，提出了一种整数规划方法求解该方程组[3].在2012 年，Walter 等人展示了如何使用MILP 优化对分组密码EPCBC 进行代数密码分析的猜测策略[4].最近又出现了一种基于MILP 求解推理系统最小化问题的新方法，该方法可用于搜索猜测确定分析的最优路径[5].

对于分组密码的差分密码分析[6]和线性密码分析[7]，构造MILP 模型是一种搜索高概率差分迹和线性迹的有效方法.Mouha 等人提出了一种基于MILP 的方法来搜索最小活跃S 盒个数，可以用来证明分组密码抵抗差分分析和线性分析的安全界[8].文献[9] 给出了基于整数规划的一般算法，该算法可以很好地评估不同分组密码活跃S 盒个数的下界.Sun 等人改进了Mouha 的方法，刻画了一些分组密码中比特级差分传播路径[10].在另一项工作中，Sun 等人对分组密码的差分特征传播进行了比特级刻画，从而发展了一种自动化计算分组密码抗差分攻击安全性的方法[11].对于ARX 结构的分组密码，Fu 等人通过刻画密码函数中的基本操作构造了寻找其差分特征和线性近似的MILP 模型[12].基于不相交的二次形式结合二次布尔函数的相关性，Shi 等人[13]从MORUS 类密钥流生成器中导出MILP 问题，并确定了MiniMORUS 和MORUS 的线性迹的相关性.

在2009 年，Dinur 和Shamir 引入了立方攻击[14]，自此之后立方攻击成功应用于流密码，在2011 年他们又提出了动态立方攻击[15].现在立方攻击已经成为了密码分析中的一个重要方法.最近立方攻击的一个重要进展是应用MILP 来确定单项式的存在性和评估目标函数的次数.Huang 等人使用MILP 技巧大大改进了Keccak 海绵函数的区分攻击[16].之后，基于MILP 模型，Li 改进了Huang 的对缩减轮Keccak-MAC-384 和Keccak-MAC-512 的密钥恢复攻击[17].在立方攻击的框架下，Song 等人提出了一种新的MILP 模型，该模型可以挑选更好的甚至最优的条件变量[18].

现在，MILP 技术已成为自动分析对称密码的强大工具.

1.1 相关工作

对于经典的密码分析方案，构造其基于MILP 的自动化模型的一个关键点是，对于一个点集S ⊆{0，1}n，如何使用尽可能少的线性整系数不等式组L，使得L在{0，1}n上的解集恰好为S，这样的L称作S的一个完全线性整系数不等式刻画(full linear integer inequality characterization，FLIIC).为方便起见，有时也称L是S的(完全) 刻画.在实际工作中，待刻画的点集S一般是由某个密码函数或密码函数中的部件F生成的.在不引起歧义的情况下，如果L完全刻画了S，也称L完全刻画了F.Mouha 等人首先提出了基于MILP 技巧的密码自动化分析算法[8]，这个算法的核心是借助哑变元对面向字的Xor操作进行了建模，即刻画了{0，1}3上的一个特殊子集.受限于刻画方式，该方法不具有通用性，难以直接应用于比特级的密码函数.

之后，研究者们致力于设计算法来寻找尽可能好的FLIIC.现有的构造算法通常采用两个步骤: 第一步，通过某种方式产生尽可能多的线性整系数不等式L′(称之为候选不等式集合)，使得L′是S的一个FLIIC;第二步，去除L′中冗余的不等式，即选择L′的一个子集L，使得L在{0，1}n上的解仍然是S.在文献[11] 中，基于计算几何的知识，Sun 等人提出了一种刻画4 比特S 盒的方法(这里可以看作刻画了{0，1}8的子集S).他们首先使用数学软件SAGE 计算了相应点集凸包的H 表示(H-representation of the convex hull of a set)，这个H 表示就是能够刻画S的一组不等式L′;然后，对L′使用贪心算法，从中每次选择一个割掉{0，1}n S中点最多的不等式(即中不满足该不等式的点最多) 加入L中，直到中的点被割完，将L集合作为输出就找到了S的一个含有更少不等式的FLIIC.这样，对于任意给定的4 比特S 盒，都能找到一个含有较少不等式的集合来刻画其差分传播.但是，使用SAGE 去计算点集凸包的方法无法解决大维数情况，即对于S ⊆{0，1}n，n ≥13，由于时间复杂度过高，无法求出相应的H 表示.针对上述过程中的第二步，Sasaki 和Todo 摒弃了贪心算法，转而采用MILP 模型去挑选最优解[19]，他们将从候选不等式集合中挑选完全刻画子集的过程等价成了集合覆盖问题，对于中的任意一点x，必须要存在L′中的一个不等式l，使得l可以割掉点x(即x不是l的一个解)，通过将这一性质转化为MILP 模型，再求解最优化问题从L′中选择最少个数的不等式去刻画S.基于集合覆盖的不等式挑选算法由于是该问题的一个完全刻画，被认为是当前第二步的最优解决方案，尽管在n较大时受限于求解器的求解效率往往难以给出最优解，但求解器在有限时间内输出的可行解已经远远优于贪心算法，因此第二步的研究基本解决，后续研究者们致力于第一步的研究，即构造完全刻画不等式的候选集合.针对比较大的n，Abdelkhalek 等人将S的刻画问题转化为求一个布尔函数最小和积的问题(the problem of minimizing the product-of-sum of Boolean functions)[20]，这一问题在其他领域已经有了非常深入的讨论，利用经典的算法，可以较快地输出8 比特的S 盒的完全刻画(即刻画{0，1}16的一个子集)，但是这样得到的不等式个数普遍过于繁多，且不能进一步约减.之后，Li 等人[21]提出了一个根据维数迭代的求解方法，对于一个点集S ⊆{0，1}n，通过现有的构造方式得到一个更低维数的点集S′⊆{0，1}n-1，假设能找到S′的一个刻画L′，则根据不等式系数以及其所刻画的点集的关系，可以将L′通过升维扩充为S的一个刻画，但这种方式局限之处在于，对S′的刻画仍然需要基于原有算法，如果得到的低维刻画集合L′中的不等式个数太多，那么L会包含更多不等式且难以约减.后来，Boura 等人进一步推进了之前的工作，得到了现有最好的结果[22].对于小维数情况，给定一组不等式L′，通过将L′中不同不等式相加组合得到新不等式，从而扩充了候选不等式选取的范围，有希望得到更好的解;对于大维数情况，提出了割球的方法，即研究能够割掉一个离散球的子集的不等式的性质，来寻找一些高质量的不等式，从而得到更好的结果.

上述给定点集的完全刻画构造算法可以应用于密码函数中的S 盒、AND 等部件的刻画，而XOR 作为一种广泛使用的密码学部件，其刻画方式的优劣对线性层、更新函数等部分起着重要的影响，通常被攻击者单独提取并研究.Boura 等人[22]基于代数的方法从理论上证明了刻画n输入的XOR 操作所需的不等式个数下界.从XOR 刻画的相关理论中可以看出，更少的XOR 数有助于构造更少不等式数目的刻画.线性变换的实现仅需XOR 操作，密码函数中所应用的线性变换都可以等价写成二元域上的矩阵的形式，Boura 等人基于上述对XOR 刻画的观察优化了SPN 函数中线性层的刻画.

我们注意到，Sun 等[23]以及Udovenko[24]独立地研究了给定子集S 的最优FLIIC 求解问题，特别是在文献[23] 中，在AES 的S 盒方面得到了比本文更好的结果.但需要说明的是，本文与这两篇文献属于完全独立的平行工作，从理论方法上来说，本文与其有着较大的差别.本工作是从不等式系数的取值范围出发建立了较为完善的理论体系，对有限点集的完全刻画进行了详尽的理论分析，并对半径为2 的球的任意子集给出了其是否被一个线性不等式完全刻画的充要条件.由该充要条件可以直接写出对应的线性不等式.这些理论成果在文献[23] 和文献[24] 中完全没有涉及.

1.2 贡献

设S是{0，1}n上的一个点集，L是一组关于n个变元的线性整系数不等式，如果L在{0，1}n上的解集恰好为S，则L称作S的一个完全线性整系数不等式刻画(FLIIC)，此时也称L完全刻画了S.记L中元素的个数为|L|，我们的目标是找到S的一个完全线性整系数刻画|L|，使得|L| 尽可能小.

首先，本文改进了Boura 和Coggia 在文献[22] 中提出的球方法.我们称B(c，r):{x|wt(x ⊕c)≤r}是一个以c为中心半径为r的球，这里x，0，1}n，Z，wt(x) 是x的汉明重量.如果S可以由一个不等式完全刻画，则称S是平整的.事实上，对于S ⊆B(c，2)，Boura 和Coggia 的球方法[22]给出了一个S是平整的充分条件.本文根据平移定理将球心移动到了原点，这样既便于理论分析，又提高了求解效率.其次对于S ⊆B(0，2)，本文首次给出了S是平整的充分必要条件.之后，又讨论了半径为3 的球的情况，提出了相应的MILP 模型，以求解S ⊆B(0，3) 的平整性.

然后，对于n ≤8，本文进一步提出了检查S ⊆{0，1}n是否能被k个线性整系数不等式完全刻画的MILP 模型，该模型可以找到S的最好刻画.

最后，将提出的新方法应用到不同的S 盒刻画中.对于4×4 的S 盒，可以快速得到最好的结果.表1 列举了刻画一些4×4 的S 盒所需的不等式个数.对于更大规模的点集，本文分析了分组密码AES所使用的S 盒，得到了比文献[22] 更好的结果，表2 列出了相关数据.

表1 刻画不同S 盒差分分布表所需不等式的个数Table 1 Number of inequalities for difference distribution tables of Sboxes

表2 刻画AES 的S 盒差分分布表所需不等式个数Table 2 Numbers of linear inequalities to characterize difference distribution table of Sbox used in AES

1.3 章节安排

本文的其余部分安排如下: 第2 节给出了一些符号和预备知识;第3 节提出了半径为2 的球上平整集合的充要条件，同时给出了MILP 模型来寻找平整集合;在第4 节中给出一个MILP 模型来寻找小维数点集的最佳刻画;第5 节将新算法应用于不同的S 盒刻画中.

2 记号和预备知识

本节介绍一些关于点集刻画的定义和定理.表3 列出了本文用到的一些记号.

表3 本文用到记号Table 3 Notations used throughout this paper

对于Πn，下面首先给出S的完全线性整系数不等式刻画(FLIIC) 的定义.

定义1(FLIIC) 令S是的一个子集，以及L是一组线性整系数不等式:

这里ai，j以及bi都是整数，0≤i ≤m-1，0≤j ≤n-1.

如果L在上的解恰好为S，则称L是S的一个完全线性整系数不等式刻画(FLIIC)，也称L完全刻画了S.

注1本文仅讨论给定点集的FLIIC 问题，对于其他刻画问题如引入辅助变元等，不在本文考虑范围之内.

对于一个给定的集合Πn，一个自然的问题是它的FLIIC 是否存在.在回答这个问题之前，在不引起歧义的情况下，本文对不等式及不等式组所用的符号l和L作一些约定.对于一个给定的不等式

下面证明FLIIC 的存在性.

定理1(FLIIC 存在性定理) 对于任意的Πn，S的FLIIC 一定存在.

证明:如果S则取L{x0≥0}即可;如果S∅，则取L{x0＜0}即可.

下面考虑非平凡情况.对任意的考虑如下不等式:

注意到x[i]⊕c[i]x[i](1-c[i])+c[i](1-x[i])，所以lc的解恰为与c的汉明距离大于等于1 的点，从而，{c}.于是L{lc|是S的一个FLIIC.

对于给定的一个集合Πn，上面已经证明S的FLIIC 总是存在的，事实上，S的FLIIC 不止一个，将S的所有FLIIC 记作C(S).为了提高MILP 模型的求解效率，通常要求|L| 尽可能地小，基于这一点，下面提出最优FLIIC 的概念.

定义2(最优FLIIC) 设Πn，C(S) 是S的所有FLIIC 的集合.对于某个(S)，如果对任意的L′(S)，都有|L|≤|L′|，则称L是S的一个最优FLIIC.

对于集合Πn，找到S的最优FLIIC 是NP-hard 问题.本文的主要工作是如何高效地找到一个(S)，使得|L| 尽可能小.为了做到这一点，首先考虑一种最简单的情况:S可以被一个线性整系数不等式完全刻画.

定义3(平整集合) 对于Πn，如果S可以被一个线性整系数不等式完全刻画，则称S是平整的，也称S是平整集合.

下面介绍平移的概念，这在本文研究中发挥着重要作用.

定义4(平移) 对于Πn以及c(c[0]，c[1]，···，c[n-1])点集S平移c定义为:

l:aixi+an ≥0 是一个线性整系数不等式，l平移c定义为:

进一步可以定义一组不等式L平移c:

对于给定的Πn以及(S)，S的平移与L的平移间可以找到对应关系，下面给出平移定理.

定理2(平移定理) 设Sl Pn，Sl可以由一个不等式l完全刻画，则对任意的，有{lc} C(c ⊕Sl).

进一步，对于S ⊆以及(S)，有Lc C(c ⊕S).

成立当且仅当

当且仅当

由lc的定义可以看出(Sl) 当且仅当{lc}C(c ⊕Sl).

设L{li}是一组整系数线性不等式，沿用之前的记号，将不等式li与其对应的解集都记作li.则

这说明Lc的解集恰好为c ⊕L，该定理得证.

3 改进的球方法

本节改进了文献[22] 中的球方法.首先介绍球的概念.

定义5(球B(y，r)) 对于以及一个非负整数r，定义一个以x为球心，以r为半径的球:

对于任意的Πn，本文旨在找到S的一个FLIIC，使得|L| 尽可能小.首先将分成几部分，这里Si都是平整的.从每个C(Si) 中各挑选一个不等式，就组成了S的一个FLIIC.球方法就是选择平整集合Si ⊆B(ci，ri)，这里ci Si ⊆在文献[22] 中，Boura 和Coggia 考虑了半径为2的球B(ci，2) 中的一些平整集合.根据平移定理，只需要考虑球心在原点的球ci ⊕B(ci，ri)B(0，ri)，对于(S)，L′(S′)，S′y ⊕S，它们的关系见图1.对于半径为2 的球B(0，2)，本文给出了B(0，2)上平整集合的充分必要条件，这个条件涵盖了文献[22] 中的球方法.除此之外，本文还将球的半径扩展到3，提出了一个新的MILP 模型，用来判断B(0，3) 上子集S是否是平整的.

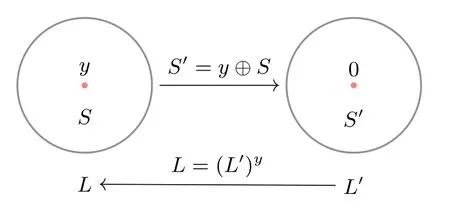
图1 L 与L′ 的关系Figure 1 Relationship between L and L′

3.1 球B(0，2) 上平整子集的充分必要条件

假设0(0，2) 并且S是平整的，线性整系数不等式

因为0，所以总是有b ＞0.为了进一步刻画S和l的系数间的关系，下面引入一些新的记号和定义.

定义6对于给定的0(0，2)，记

如果一个不等式l完全刻画了，则关于l的系数有如下结论.

命题1设0(0，2)，假设{l:aixi ≥an}C，则

(1)an ＞0;

(2) ∑i∈I ai ≥an，这里I是{0，1，···，n-1}的子集，且其所含元素个数|I|≥3;

(3)ai ＜an当且仅当eiΓ;ai ≥an当且仅当ei

(4) 如果ai ≤aj，则Γi，j ⊆Γj，i.进一步，对于eiΓ 和ej有Γi，j ⊆Γj，i.

证明:因为0，所以an ＞0;因为所有汉明重量大于等于3 的点都在中，所以(2) 成立;根据Γ 的定义，(3) 是平凡的;对于k/i，j，如果ai+ak ≥an，则aj+ak ≥ai+ak ≥an，即如果ei ⊕ek则ej ⊕ek从而Γi，j ⊆Γj，i.

根据以上命题，如果S是平整的(从而也是平整的)，则对于i/j，要么有Γi，j ⊆Γj，i，要么有Γj，i ⊆Γi，j.这类似于两个整数ai和aj，它们总是可以比较大小.为了描述这一性质，下面给出有序集的定义.

定义7(有序集) 设0(0，2)，如果下面两个条件成立:

(1) 对于i/j，要么有Γi，j ⊆Γj，i，要么有Γj，i ⊆Γi，j;

(2) 对于eiΓ 和ej有Γi，j ⊆Γj，i，则称S是一个有序集.

在确定S是否是有序集时，事实上并不需要比较所有的Γi，j，下面引理说明了这一点.

引理1设0(0，2)，如果Γi，i+1⊆Γi+1，i对所有的i0，1，···，n-2 成立，则对于0≤i ＜j ≤n-1，Γi，j ⊆Γj，i，从而S是一个有序集.

证明:先证明对于k ≥2，有Γ0，k ⊆Γk，0.只需证明对于某个eiΓ0，k，有eiΓk，0.

当i ＞k时，由于ei ⊕e0所以eiΓ0，1.再考虑Γ0，1⊆Γ1，0，所以eiΓ1，0，得到ei ⊕e1;继续考虑Γ1，2⊆Γ2，1，···，Γk-1，k ⊆Γk，k-1，最终可以得到ei ⊕ek从而eiΓk，0.

当i ＜k时，类似上面证明，可以得到ei ⊕ei-1这时考虑ei-1Γi，i+1⊆Γi+1，i，最终可以得到ei-1⊕ek即ekΓi-1，i，而Γi-1，i ⊆Γi，i-1，从而也可以得到ek ⊕ei综上，得到了Γ0，k ⊆Γk，0.

对于0＜j ＜k，同理可以证明Γj，k ⊆Γk，j，引理得证.

注2假设j ＜k以及Γk，j ⊆Γj，k.取{0，1，···，n-1}上的一个置换σ，其对应为σ(j)k，σ(k)j，对于i/j，k，σ(i)i，则有Γσ(j)，σ(k)⊆Γσ(k)，σ(j).依此类推，对于一个有序集，总是可以找到一置换σ，使得对于所有的i0，1，···，n-2，总有Γσ(i)，σ(i+1)⊆Γσ(i+1)，σ(i).为了方便起见，后面总是考虑σ是恒等映射的情况.

根据以上分析，对于一个有序集S，只需考虑Γi，i+1⊆Γi+1，i.此外，下面这条性质也十分重要.

引理2设0(0，2)，如果Γi，i+1⊆Γi+1，i对所有的i0，1，···，n-2 成立.对于i ＜j，以及h，k/i，j，有:

(1) 如果ei ⊕ej S，那么对任意的k ＞j，有ei+ek对任意的h ＞i，有eh ⊕ej S;

(2) 如果ei ⊕ej S，那么对任意的k ＜j，有ei+ek S;对任意的h ＜i，有eh ⊕ej S.

证明:对于(1)，根据引理1，Γj，k ⊆Γk，j，如果eiΓj，k，自然有eiΓk，j，即ei ⊕ek同理，对于h ＞i，考虑ejΓi，h ⊆Γh，i，即ej ⊕eh

(2) 可以看作(1) 的推论.

有了前面的准备，接下来将证明对于0(0，2)，可以由一个不等式完全刻画当且仅当S是一个有序集.先考虑一种简单的情况B(0，1)⊆S ⊆B(0，2).

引理3设B(0，1)⊆S ⊆B(0，2).则SB(0，1) 或B(0，2) 当且仅当Γi，i+1Γi+1，i对所有的i0，1，···，n-2 成立.

证明:必要性是显然的，下面证明充分性.

如果对某个i，有Γi，i+1Γi+1，i/∅，下面证明Γi，i+1{0，1，···，n-1}{i，i+1}.否则，如果k/Γi，i+1，就可以得到i，i+1/Γk，k-1，Γk，k+1，因此k-1，k+1/Γi，j，依此类推，最终得到Γi，j∅，这与假设Γi，i+1Γi+1，i/∅矛盾.从而Γi，i+1{0，1，···，n-1}{i，i+1}，这对应SB(0，1).此时可以验证xi ≥2().

接下来，对于一个有序集B(0，1)⊆S ⊆B(0，2)，将构造一个不等式l，使得().

定理3对于B(0，1)⊆S ⊆B(0，2)，Γi，i+1⊆Γi+1，i对所有的i0，1，···，n-2 成立.按如下方式构造n+1 整数:

这里i0，1，···，n-2，并且

这里a0是一个满足下列方程的正整数:

证明:首先说明总是存在a0满足方程(4).这是因为a0+a1+a23a0+c1以及an2a0+c2，这里c1和c2是两个常数，其值大小由a1，a2，···，an-1的构造决定.因此当a0足够大时，总有3a0+c1≥2a0+c2.

再根据a0，a1，···，an的定义，有a0≤a1≤···≤an-1＜an，并且

这里I ⊆Zn并且|I|≥3.因此，下面只需要验证对于i ＜j，

如果a0a1···an-1，这对应Γi，i+1Γi+1，i对所有的i0，1，···，n-2 成立，这对应引理3 的情况，此时该定理成立.

接下来只需考虑至少存在一个i ≤n-2，使得ai严格小于ai+1.如果i ＜j且aiaj，则使用来代替ai和aj，则由升链

可以得到一个长度大于1 的严格升链这里n′＞1 以及a0

再根据e0⊕en-1是否在中分两种情况讨论.

同样的方法，就可以证明ai+aj ≥an当且仅当ei ⊕ej即方程(5)成立.

·e0⊕en-1.这种情况下，对于ai类似前面的证明，一定有ei ⊕en-1否则与a0＜ai矛盾.再根据引理2，一定有e0⊕ei S，i ≥1.此时就考虑下面这条升链

和情况e0⊕en-1一样，同样可以证明方程(5)成立，这里不再赘述.

下面举例说明定理3 如何操作.

例1设S{(0，0，0，0)，(0，0，0，1)，(0，0，1，0)，(0，1，0，0)，(1，0，0，0)，(1，1，0，0)，(1，0，1，0)}，则S ⊆并且B(0，1)⊆S ⊆B(0，2).可以计算得到

定理3 解决了情况B(0，1)⊆S ⊆B(0，2)，对于一般的0(0，2)，也有类似的结论.

定理4对于0(0，2)，令Γ{e0，e1，···，ek-1}，这里k ≤n，即当i ≤k-1 时，ei S，当i ≥k时，ei;Γi，i+1⊆Γi+1，i，对所有的i0，1，···，n-1 成立.则有如下结论:

· 如果ei ⊕ej对所有的i/j以及j ≥k ＞i成立，则取

这里k ≤j ≤n-1.再考虑下面这样一个集合

证明:根据定理3，第一种情况是显然的.

如果0(0，2) 可以由一个不等式完全刻画，自然地S是一个有序集，根据前面讨论，实际上定理4 通过构造的方法给出了S可以由一个不等式完全刻画的充分必要条件.至此，本节完全解决了r2的情况，对于更大的r，还没有相关结论，但是r ≤2 的情况已经足够在实际中使用.接下来将介绍如何使用球方法构建MILP 模型来寻找相应的不等式.

3.2 寻找平整集合的MILP 模型

本节提出了寻找半径为r的球B(0，r) 上的平整集合的MILP 模型.因为要证明模型的正确性需要用到图的连通性的相关知识，下面先介绍一些关于连通性的内容.

定义8(路径) 设Πn.对于x0，x1，···，xm S，如果对所有的i0，1，···，m-1，都有d(xi，xi+1)1，则称(x0，x1，···，xm) 是S中一条连接x0与xm的路径.

有了路径的概念，接下来给出连通性概念.

定义9(连通性) 设Πn，如果对任意的x，，都能在S中找到一条连接x和y的路径，则称S是连通的.

有了连通性的概念，可以发现所有的平整集合都是连通的.

定理5设Πn以及S的元素个数|S|≥2.如果S可以由一个不等式刻画，则对于任意的x，，存在S中的一条连接x和y的路径.

证明:设不等式aixi ≥b完全刻画了S，这里b和ai都是整数，i0，1，···，n-1.记函数f(x)aix[i].

对于任意x，，有f(x)≥b以及f(y)≥b.下面证明存在中的一些点x0x，x1，···，xty，使得f(xi)≥b对所有的i0，1，···，t成立，并且d(xi，xi+1)1 对所有的i0，1，···，t-1 成立，即(x0，x1，···，xt) 是S中连接x和y的一条路径.

记x(x[0]，x[1]，···，x[n-1]) 以及y(y[0]，y[1]，···，y[n-1]).根据x和y分量的值定义如下三个集合:

设集合I有p个元素I{h1，h2，···，hp}.记x0x，按如下方式构造p个点:

其中，eh表示上的一个单位向量，其第h个位置为1，其他位置都为0.

根据上述构造，首先d(xi，xi-1)1 对i1，2，···，p成立，因为xi与xi-1只相差一个单位向量.其次，下面说明f(xi)≥f(xi-1)，这是因为:

根据I的定义，xi-1[hi]1 时，有＜0;xi-1[hi]0 时，有≥0;所以始终有f(xi)-f(xi-1)(1-2xi-1[hi])≥0.

设集合J有q个元素J{k1，k2，···，kq}.按如下方式构造q个点:

类似x1，x2，···，xp的构造，d(xj+p，xj+p-1)1 以及f(xj+p)≤f(xj+p-1) 对j1，2，···，q成立.

因为WI∪J，所以xp+qy.

综上，有

即上述构造的点x0，x1，···，xp+q都在集合S中，从而(x0x，x1，···，xp+qy) 是S中一条连接x和y的路径.

当n或者r比较大时，很难求解模型M(y，r).但是如果已经得到了一个不等式，那么从这个不等式出发可以高效地得到更好的结果.具体来说，如果模型M(y，r) 可以高效求解rr0，但是对rr0+1很难求出结果，那么对rr0+1 可以提出一个启发性算法.假设通过M(y，r) 得到了不等式l，则可以用模型M*(y，r，l) (模型2) 来计算一个新的不等式l*，该不等式满足l*⊆l.

注4模型M(y，r) 和M*(y，r，l) 求出的不等式对应的解集都是平移之后的，即y ⊕Sy ⊆B(0，r)，最初需要的集合还需要再平移(和y异或).需要指出的是平移操作可以明显提高模型求解效率.对AES所使用的S 盒进行实验，对于r2，使用平移操作后求解时间为7646.18 s，而不使用平移操作需要11 384.26 s，可见平移操作在提高模型求解效率方面确有帮助.

3.3 不等式系数的界

在模型M(y，r) 中，对于整数变量要确定其上下界，通常来说，很难精确地给出这个界.如果取的界太小，那么求解出的|Sy| 也可能很小，达不到|Sy| 尽可能大的要求;如果界太大，则可能会增大模型求解空间，从而影响模型求解效率.本节考虑B(0，2) 上的平整集合时，可以给出相应的精确的界.对于0(0，2)，S是平整的，根据定理4，可以构造从而可以得出l系数的界.

证明:不妨假设n′≥3 (此时3n′-5≥4).只需要证明定理4 构造的不等式系数可以由M界定即可.

先考虑a0a1＜a2和a0+an′＜an的情况，注意到

由ai+1最多比ai大1，所以an′-1≤a+n′-3.于是ana2+an′-1≤a+a+n′-3，而a0+a1+a23a-2，为了保证a0+a1+a2≥an，只需要3a-2≥2a+n′-3 即可.于是可以取an′-1.由此可以算出an ≤3n′-5.

对于其他情况，即a0，a1，a2与an的大小关系，其讨论过程和上面的情况一样，这里不再赘述.

假设S能够被aixi ≥an完全刻画，这里-M ≤a0，a1，···，an ≤M，M是一个正整数，现给出如下模型3 来求解最小的M以及对应的a0，a1，···，an.

4 对小维数点集的最优刻画

对于给定点集S，本节提出了一个判断S是否可以被k个线性整系数不等式完全刻画的MILP 模型.假设(S)，那么L应满足下面两个条件:

(1) 对每个以及，应该有;

(2) 对每个至少存在一个不等式l′使得

假设|L|k以及li:ai，jxj ≥bi L，i0，1，···，k-1.对于第一个条件，只需要令

对所有的i0，1，···，k-1 以及成立.对第二个条件引入新的二元变量di，y，i0，1，···，k-1，这里di，y1 代表di，y0 代表.为了描述di，y，引入如下约束:

当M足够大时，可以看到:

(1)di，y1

(2)⇒di，y0.

对于每一个点因为总是存在一个不等式使得y/l，所以要引入如下约束:

下面列出所有的约束条件:

对于一个正整数k，如果模型有解，那么就得到了(S) 满足|L|k.否则对任意的(S) 就有|L|≥k+1 .令k1 开始逐步增大，直到模型有解，最后就可以得到S的最优刻画.

5 应用

本节将新方法应用到分组密码S 盒的差分分布表刻画中，和现有的方法相比，得到的不等式个数更少.设S是一个S 盒，S的差分表记为S，即

对给定的8×8 S 盒，以AES 使用的S 盒为例，使用模型M(y，r)，对于r2，对i0，1，···，15，取Mi50，M′800，M1610，利用模型M(y，2) 得到的不等式个数小于3100;对于r3，很难得到M(y，3) 的最优解，为了解决这一问题，固定M(y，3) 的求解时间最终得到一组不等式L′，然后进一步求解模型M*(y，2，l)，这里l是M(y，2) 的解，得到另外一组不等式L′′.最后基于L′和L′′得到2740个不等式.表2 列出了关于AES 使用的S 盒的一些结果;对于4×4 的S 盒，我们使用了第4 节中的方法，结果见表1.