公钥密码安全强度刻画概述*

林 申，陈 洁，王陆平

1.华东师范大学 软件工程学院 上海高可信计算重点实验室，上海200062

2.苏州科技大学 电子与信息工程学院，苏州215009

3.江苏省电梯智能安全重点建设实验室，常熟215500

1 引言

现代公钥密码方案的安全性是建立在困难性问题假设上的，具有可证明安全性(provable security)，即: 若求解该问题假设是困难的，则称该公钥密码方案是安全的.这也是公钥密码学与对称密码学在本质上的一大不同.公钥密码方案的安全性与困难问题假设的种类紧密相关，按困难问题对公钥密码方案进行分类也是一类常见的分类标准.

如图1 所示，现存的公钥密码方案可大致分为两类: 基于经典数论问题的方案和基于抗量子攻击困难问题的方案.经典数论体系下公开的公钥密码方案以1976 年提出的Diffie-Hellman 密钥交换算法[1]为开端，可根据嵌入困难问题的不同分为三类: 即基于大整数分解问题、基于离散对数问题和基于椭圆曲线问题的方案.然而，随着量子计算机的出现，经典公钥密码体制的安全性受到了极大的挑战.Shor 算法的提出，使得破解RSA、DSA、ECDSA 算法成为了可能[2].因此，抗量子攻击的新密码方案在近些年应运而生，被称为后量子密码.相似地，根据困难问题的不同，可将常见的后量子密码分为五类:基于格问题、基于编码问题、基于哈希函数问题、基于超奇异椭圆曲线同源问题和基于多变量二次方程组问题的方案.由于方案安全性的内核和攻击者的能力都有本质不同，经典公钥方案和后量子公钥方案的安全性评估标准和结果都有明显的区别.

图1 根据困难问题分类的公钥密码方案Figure 1 Public key cryptography schemes classified according to difficult problems

安全强度在密码方案的实例化中具有非常重要的意义，具象的安全标准对方案参数的设置有很强的导向作用.譬如，在基于配对的密码方案的实例化中，Costello 等人提出，BLS24 椭圆曲线(嵌入度/安全乘数k24 的Barreto-Lynn-Scott 曲线[3]) 非常适合构造192，224，256，288 和320 位的安全强度较高的配对方案[4].此外，同族中k12 的BLS12 椭圆曲线非常适合构造192 位安全的配对.在后量子密码方案的实例化中也是如此.2022 年郝世迪等人提出了一种基于模格MLWR 密钥封装的参数优化，针对NIST 后量子标准化选定的Saber 方案的三种变体都提出了一组新参数，使其在安全强度、错误率和带宽方面获得了更好的平衡，特别是针对参数更为轻量级的变体LightSaber 方案的新参数，使其在保持相当于128 位AES 安全强度的前提下，密码分析所需的量子门电路规模由2107提升至了2111(量子门电路规模的评价标准详见2.2 节)，并使得各参数的规模都有所缩小[5].安全强度的提升往往被看作证明方案可用性的一大因素.

目前，国内学界在经典密码方案、后量子密码方案和密码应用方案的安全性上都有相应的研究和总结.在经典密码体系的安全强度介绍上，2016 年，孙权总结并对比了国内外主流的对称加密、非对称加密、杂凑等主要加密算法的安全强度要求，并针对不同类型的软件应用场景，结合计算机算力的发展趋势，提出当前主流加密算法的密钥强度建议[6]，但该文对公钥加密安全强度的总结较为片面，仅以加密方案为单位介绍了ECC 算法和RSA 算法的密钥长度和安全强度的关系(如1024 位密钥的RSA 算法对应80 位的安全强度)，缺乏从困难问题出发的安全强度梳理，并且在近三年内，缺乏更新的综述跟进公钥加密方案安全性的发展.在后量子密码体系方面，目前综述性总结较少，且集中在对称密码方面.2021 年，梁敏等人对后量子对称密码的安全强度进行了概述，分类介绍了后量子对称密码的研究进展状态，归纳总结了各项成果之间的关联及其机理[7]，仍缺乏对后量子公钥密码研究及其安全性的系统性总结.此外，对使用经典公钥加密和后量子公钥加密方案的商用密码方案，目前国内的研究还处在对国家标准的总结与对比层面[8]，少有落地于具体密码产品安全强度评估的研究总结，在场景应用安全性上也缺乏相应的安全建议.

综上，国内学界研究仍缺乏对经典公钥密码方案和后量子公钥密码方案安全性定量评估的系统介绍，且缺乏结合密码学实际应用的公钥密码方案的安全性评估介绍.为弥补这些缺失，本文将以公钥密码方案嵌入的困难问题为分类标准，定量刻画现有的主流公钥密码方案的安全性，并结合目前商用的公钥密码方案应用，分析现有的公钥密码方案的安全性的总体现状和存在的隐患，并对未来的安全性提升的研究和密码算法的安全应用进行了展望.希望能为公钥密码方案的安全性优化研究提供一些参考和帮助.

本文的第2 节将介绍安全强度的概念，并阐述在数论困难问题下的密码(下文统称经典公钥密码) 和在抗量子攻击困难问题下的密码(统称后量子公钥密码) 安全强度的具体定义.第3 节将介绍常见经典公钥密码方案的安全强度.第4 节将介绍常见后量子密码方案的安全强度级别.第5 节将从第3—4 节中提到的密码方案的现实应用出发，介绍若干中外企业在商用安全服务中使用的公钥密码方案及其安全强度分析.第6 节将对目前学界公钥密码方案的安全性现状进行总结和展望.

2 公钥密码方案的安全强度定义

密码方案定量的安全性被称为安全强度或安全等级(以下统称安全强度)，通常指在当前最佳有效攻击方式下，在密码方案取某参数时，解决困难问题的计算开销.

本文使用的安全强度定义是根据美国国家标准与技术研究所(National Institute of Standards and Technology，NIST) 在SP800-57 第5 版密钥管理建议中给出的定义[9]作适应性修改得到的.

定义1(密码方案的可比安全强度) 若给定密码方案A 和方案B 的参数集，确定A 和B 的密钥所需的计算开销大致相同，则称密码方案A 和方案B 对于该参数集具有可比安全强度.

由定义可知，安全强度是基于参照的密码方案产生的，而非绝对的.在目前常见的公钥密码安全强度刻画的标准中，对称密码方案往往是强度比较的媒介，常用的又以AES 为多[10].

本文在2.1 和2.2 节将会根据经典公钥和后量子公钥的不同特性，给出具体的安全强度定义.需要指出的是，关于安全强度，学界一直存在着不同的定义，不同的标准化机构之间有不同的定义方式.譬如，ENISA[11]和IETF[12]等机构给出的安全强度建议都与NIST 不同，但目前多数密码方案评估都以NIST 为准，因此，本文采取了NIST 的标准化规定.

2.1 经典公钥密码方案的安全强度定义

本文在经典公钥体系下衡量安全强度的方法如下:

定义2(经典公钥密码方案的安全强度) 若某公钥密码方案确定密钥所需的时间与某对称密码确定密钥所需的时间近似，则该公钥密码方案的安全强度等于该对称密码的密钥长度.

从具体例子而言，若一个对称密码算法的密钥为X位，对明文进行加密，并比较所得密文和目标密文是否一致所需的时间为T，则完成穷举密钥平均需要2X-1T的时间.如一个公钥密码算法被攻破的平均时间(即解决困难问题的时间) 与2X-1T相近，则称该密码算法具有X位的安全性[10].

经典公钥密码的安全强度通常有{80，112，128，192，256}几种，分别对应不同对称密码基准的密钥长度，如表1 所示.其中112 位的2DTEA (有2 个独立密钥的DES 算法) 在选择明文攻击或已知明文攻击下需280次操作可确定密钥[13];168 位的3DTEA[14](有3 个独立密钥的DES 算法) 在中途相遇攻击下(meet-in-the-middle attack) 需2112次操作可确定密钥[15];目前对AES (advanced encryption standard) 最有效的密码分析算法没有对其安全性产生太大影响[16]，其安全强度等于密钥长度.

表1 经典公钥密码方案的常见安全强度Table 1 Typical security strengths of classical public key cryptography schemes

在实际应用中，随着密码分析方法的不断更新，公钥密码的实际强度会更弱，本文阐述的是密码方案在理论实验中的安全强度.Bernstein 在2013 年提出，一些公钥密码系统(如RSA 和ECC) 遭到更强的攻击时，其在实际应用中的安全强度与标准机构提出的安全强度相比，会产生1.1—1.5 倍的差距[17].大型量子计算机的产生也会削弱经典公钥密码的安全强度，但考虑到量子计算的落地普及还需一定时间，本文暂不把这一因素纳入到经典公钥安全强度的讨论范畴内.

2.2 后量子公钥密码方案的安全强度定义

本文提出的后量子公钥密码方案的安全强度概念参照的是NIST 在后量子密码学标准化方案征集中给出的评估标准[18]，同样采取与对称密码等价的思想，但用安全强度等级的概念代替了具体的安全位数.采用该方法的原因是目前学界对量子计算机的性能认知有限，研究者需要根据量子计算机的性能发展，细化后量子公钥密码方案的安全强度.

定义3(后量子公钥密码方案的安全强度等级) 若攻破某后量子公钥密码方案所需的经典门电路/量子门电路数量，与攻破某密钥长度的AES 密码所需的经典门电路/量子门电路数量近似，则该后量子公钥密码方案的安全强度等级等于该AES 密码的安全强度等级.

现有研究已给出了使用Grover 算法对AES-128/192/256 攻击所需的门电路规模的估计[19]，在这基础上可以得到三种不同的安全强度等级，如表2 所示[20].其中MaxDepth 是指一定时间内可串行的门电路数量，可将量子攻击限制在固定运行时间内，其范围大致在[240，264] 个逻辑门之间(等价为1 到10 年内目前理想的量子架构能执行的逻辑门数量)，最高不会超过296(等价为光速原子级量子位在一千年内可以执行的逻辑门数量)[21].引入该常量可以限制攻击算法的计算时间，并将攻击者的能力控制在合理的范围内.

表2 后量子公钥密码方案的常见安全强度Table 2 Typical security strengths of post-quantum public key cryptography schemes

在后量子密码方案的安全性衡量上，使用经典门电路规模和量子门电路规模等价安全强度等级的方法是同时存在的.比如，NTRU 方案的说明文档中，衡量安全强度使用的就是RAM 模型下混合攻击的core-SVP 成本[22];另有一些研究，如文献[5，23]，则同时用到了经典电路和量子电路混合攻击的core-SVP 成本来衡量安全性.

3 经典公钥密码方案的安全强度

3.1 经典公钥的困难问题

经典公钥密码方案的安全强度论述将分为三类展开: 基于大整数分解困难问题的方案(integer factorization problem，IFP)、基于有限域离散对数困难问题的方案(discrete logarithm problem on finite field，DLP-FF) 和基于椭圆曲线离散对数困难问题的方案(discrete logarithm problem on elliptic curve，DLP-EC).三类困难问题的数学表述如表3 所示.

表3 经典公钥困难问题的数学表述Table 3 Mathematical expression of classical public key hard problems

以上三种问题使用经典计算机都难以破解，即使出现了若干比朴素计算更快的密码分析算法，譬如针对整数分解问题的普通数域筛选算法(N位整数分解的复杂度为expo(1)))[24]) 等，可以将时间复杂度控制在多项式级和指数级之间，但目前没有经典计算机可应用的多项式算法破解这三类问题.常见的基于大整数分解问题的密码方案有RSA 方案[25]、Rabin 方案[26];常见的基于有限域离散对数问题的密码方案有DSA 方案[27]、DH 密钥交换方案[1，28]、ElGamal 方案[29];常见的基于椭圆曲线离散对数问题的密码方案有椭圆曲线DH 密钥交换方案(EC-DH)[30]、椭圆曲线DSA方案(EC-DSA)[31]、椭圆曲线ElGamal 方案(EC-ElGamal)[32]、国密SM2 方案[33].

3.2 三类经典公钥的安全强度

三类困难问题的安全强度如表4 所示[10]，以公私钥的长度为主要变量(其中k为模数n的长度，L为公钥长度，N为私钥长度，f为椭圆曲线基点G的阶，k和f也常被简称为密钥长度).

表4 经典公钥密码的安全强度Table 4 Security strength of classical public key cryptography

关于在表4 中未给出的大整数分解和有限域离散对数密码方案实例化参数，可以通过NIST 给出的公式进行安全强度的计算.对于密钥长度为L的大整数分解密码方案而言，对应的对称密码位数x(可大致等同于安全强度) 可用公式(1)计算[34]:

对于公钥长度为L、私钥长度为N的有限域离散对数密码而言，其安全强度y可用公式(2)计算(其中x为将L代入公式(1)中的计算结果).

到2030 年，112 位的安全强度的密码方案不允许被用于加密和签名的数据保护，仅可被用于解密和验证签名.2031 年以后，若要在数据保护和验证处理上都保有足够的安全性，那么一个密码算法至少需要有128 位及以上的安全性[10].

4 后量子公钥密码方案的安全强度

后量子公钥密码方案的阐述将分为以下几部分展开: 基于格问题的密码方案、基于编码问题的密码方案和基于其他抗量子攻击困难问题的密码方案.本节中的安全强度阐述将在困难问题下，以具体密码方案为单位展开，因为同一类后量子困难问题下的方案参数选取差异化较大，且后量子公钥密码发展还不成熟，目前仍未有一个完整的标准化体系.

4.1 基于格问题的密码方案

格可被看作一组n维空间上的线性网格点，其定义如下:

定义4(格) R 为实数域，Z 为整数域，给定n个线性无关的向量b1，b2，···，bnRm，那么格是这n个向量的任意线性组合的集合，即:

{b1，b2，···，bn}为格的基向量，也可写成基矩阵B的形式.

格上的若干数学困难问题，常用的包括最短向量问题(shortest vector problem，SVP)、最近向量问题(closest vector problem，CVP)、小整数解问题(small integer solution problem，SIS)、带错学习问题(learning with error，LWE) 等，即使对于量子计算机而言，也是难解的.这四类问题的定义如表5 所示.

表5 常见格困难问题的定义Table 5 Definition of typical lattice hard problems

本文将以下安全高效的格密码方案纳入调研的范围，分别为: NTRU 方案(融合了NTRUEncrypt 和NTRU HRSS-KEM 两个方案)、CRYSTAL-KYBER 方案和CRYSTAL-DILITHIUM 签名方案.

4.1.1 NTRU

NTRU 方案是1998 年基于格上SVP 问题构造的首个格基公钥加密方案[35].本文采用的NTRU 方案是NIST 后量子标准化第三轮入围的版本，包括了NTRU 的加密和密钥封装算法，其中加密算法沿用的是NTRU-HPS 算法[3]，密钥封装沿用的是NTRU-HRSS 算法[36].NTRU 在本地模型(local model，计算模型中的信号以有限的速度传播，如单带图灵机和超大规模集成电路VLSI)和非本地模型(non-local model，计算模型允许在任意距离进行单位成本通信，如随机存取机器、布尔电路和Clifford+T 量子电路)下的安全性有明显区别[37].前者只允许模型信号以有限速度传播，整体安全性较高;后者允许任意距离内的单位成本通信，整体安全性较低.

表6 为NTRU 方案的安全强度等级列举(Category 1，3，5 的定义见表2)，其中参数中的N可确定多项式环的最高次数N-1，q为大模数，参数名设置往往是“NTRU-HPS+N+q” 或“NTRU-HRSS+N”的格式.

表6 NTRU 方案的安全强度等级Table 6 Security strength levels of NTRU

NTRU 方案安全强度等级的选取是大致根据原始攻击(结合了维度约简算法[38]和正交投影约简算法[39]) 和Howgrave-Graham 混合攻击[40]的core-SVP 块约简的位操作成本决定的，其中会有一些数据略小于表2 中的门电路规模标准(如(local) NTRU-HPS2048677 和(non-local) NTRU-HPS4096821)，但设计者也指出，在分析中未考虑的额外成本如内存访问成本等，弥补了规模上的差距.同时值得指出的是，目前给出的NTRU 参数集仍存在一定的隐患，若Ducas 关于本地模型复杂度的安全性估计[41]是正确的，那么表格中的本地模型安全强度等级需要向下修正.

4.1.2 KYBER 和DILITHIUM

CRYSTAL-KYBER[23]和CRYSTAL-DILITHIUM[42]同属于代数格密码套件[43](cryptographic suite for algebraic lattices，CRYSTAL) 的原语族，基于模带错学习问题(module learning with errors，MLWE) 问题构建.KYBER 和DILITHIUM 各有三组不同的参数集，KYBER 可实现Category 1/3/5的安全等级，DILITHIUM 可实现Category 2/3/5 的等级(本文仅讨论了3/5 两种等级).KYBER 和DILITHIUM 共享一个框架，其安全等级的改变可以简单地通过改变算法中使用的块矩阵的顺序来实现.KYBER 和DILITHIUM 密钥的大小都很小，对于实际的应用较为友好，特别是KYBER，已经在一些互联网的安全服务中有了多处应用.经过4 轮的选拔后，两个方案都已进入了NIST 后量子标准化的最终候选算法(selected algorithm 2022)[44].

和NTRU 的提出者直接使用core-SVP 成本对标安全强度等级不同的是，KYBER 和DILITHIUM的NIST 说明文档中提到了基于core-SVP 成本虽然可以得出较为保守的安全性，但较为粗略.在KYBER和DILITHIUM 方案中，设计者使用了更贴合现实的攻击算法[41，45，46]对经典门电路的规模数据进行了修正，其数据会略高于格原始攻击的core-SVP 成本，但更接近现实情况.

表7 为KYBER 方案和DILITHIUM 方案的安全强度等级列举，在KYBER 方案中，n和q分别决定多项式模环RqZq/(Xn+1)的系数模和最高次数，k为矩阵的维数，改变k可调节方案的安全性.在DILITHIUM 方案中，定义多项式环的n256，q8380417，表中τ为签名中间变量c中±1 的数量，(k，l) 为随机矩阵A的维数，η为私钥每位的取值范围(si Sη)，ω为签名hint 中1 的最大出现次数.

表7 KYBER 和DILITHIUM 方案的安全强度等级Table 7 Security strength levels of KYBER and DILITHIUM

4.1.3 本节小结

本节总结了三个基于格的密码方案，分别为 NTRU、CRYSTAL-KYBER 和 CRYSTALDILITHIUM，这些方案都有较为完善的若干参数集，可以适应不同场景的安全性，在效率优先的情况下，往往Category 1 的安全等级即可满足需求，如果要求更高的安全等级，上述方案也都可以满足需求.虽然在安全强度等级上二者都可以符合标准化的需求，但KYBER 和DILITHIUM 相较于NTRU 给出的安全强度评估的出发点更加细致，也是CRYSTAL 密码套件的优势所在.

基于格问题的密码方案也是入选NIST 后量子标准化最终确定方案名单中最多的，包括KYBER、DILITHIUM 和FALCON[47]，是目前最有前景且总体最稳定的抗量子密码方案类别，兼具安全性和高效性，因此，对于后量子公钥的应用可以多侧重于格密码，以保障敏感信息的安全性和信息传输的高效性.

4.2 基于编码问题的密码方案

基于编码的密码方案依赖的困难问题往往是纠错码上的伴随式译码问题 (syndrome decoding，SD)[48]及其衍生的困难问题，与寻找码字问题(codeword finding，CF) 及其衍生问题，分别定义如下.

定义5(计算型伴随式译码问题) 对于一个码长为n，信息位数为k的线性码，给定一个二元(nk)×n矩阵H、一个码字0，1}n-k和一个整数w ＞0，找出一个具有汉明重量小于等于w的码字x，使得Hx⊤y⊤.

定义6(判定型伴随式译码问题) 对于一个码长为n，信息位数为k的线性码，给定一个二元(nk)×n矩阵H、一个码字0，1}n-k，判断y是由伴随式σ(x)Hx⊤生成的，还是随机生成的.

定义7(寻找码字问题) 给定一个二元(n-k)×n矩阵H和一个整数w ＞0，找出一个汉明重量小于等于w的码字x，使得Hx⊤0⊤.

本文调研的基于编码问题的方案有2 个: Classic McEliece 和BIKE.其中Classic McEliece 是进入NIST 后量子标准化选拔第三轮正式候选的编码方案，BIKE 为第三轮的备用方案.

4.2.1 Classic McEliece

Classic McEliece 方案是NIST 第三轮方案提交中历史最为悠久的方案，是由OW-CPA (one-way CPA) 的McEliece PKE 方案转化得到的CCA2 密钥封装机制(key encapsulation mechanism，KEM)，与传统的公钥加密机制不同的是，密钥封装加密的目标更为明确，是为了保护通信中的对称密钥，被用于通信的混合加密中.McEliece PKE 由McEliece 于1978 年提出[49]，至今仍有足够强的安全性.McEliece的安全性基于计算型伴随式译码问题的变体，使用的码为Goppa 码.

目前的Classic McEliece 方案融合了第一轮的Classic McEliece 方案和NTS-KEM 方案.Classic McEliece 也是三个方案中提供的参数集最多的，Category 1/3/5 每个分类中至少都有两种不同的参数集[50].McEliece 的优势在于长期稳定的安全性保障，以及较小的密文大小，但其公钥大小过大也成为了一大劣势.

针对基于编码的密码方案最有效的攻击方法是信息集攻击(information-set decoding，ISD)[51]，较为有效的算法包括Stern 算法[52]、BJMM 算法[53]等.在Classic McEliece 的官方文档中使用的是Stern算法变体[54]的经典门电路规模(位操作次数) 等价的参数集安全强度等级，因此，本文也采用相同的数据[55].除了官方文档中使用的主流数据，近年也有新的研究对高效密码分析算法的操作复杂度数据进行了修正，例如文献[56]，但截至目前，相关研究并未对Classic McEliece 方案的安全性产生较大的冲击.

Classic McEliece 方案不同参数设置及其安全强度等级如表8 所示，其中m为码长，nlog2q，q为有限域的模，t为最大纠错位数，f(z) 和F(y) 为两个有限域上的多项式，用于生成码.对于实验数据低于NIST 标准的情况，Classic McEliece 的文档也做出了说明，指出使用Stern 算法的实际总开销大于计算开销.表中第二行的McEliece-4608-096 参数集的安全强度评估自2020 年来一直存在争议，在实验中，该规模略小于2207，有研究者指出[57]，即使存在方案设计者所说的可观存取成本，数据仍然难以达到Category 3 所需的门槛.

表8 Classic McEliece 方案的安全强度等级Table 8 Security strength levels of Classic McEliece

4.2.2 BIKE

BIKE 方案是用于密钥封装的方案，发布于2017 年[58].BIKE 方案是受到使用准循环码实例化McEliece 方案的启发，使用的是中密度准循环奇偶校验码，方案基于准循环码的伴随式译码问题和寻找码字问题构建.BIKE 方案在NIST 第二轮方案中并未提交符合Category 5 的参数集，且缺乏CCA 安全的证明，故被暂时列为第三轮的备选方案，但在第三轮的提交中，上述的两个缺陷都已经被补全.BIKE 方案的参数设置和安全强度等级如表9 所示，共有三组不同的参数，r为块大小，也是校验位的长度，n2r为纠错码的码长，k为信息位长度，w为行汉明重量，t为错误汉明重量.此处的数据出自文献[56] 的实验，采用的是BJMM 算法攻击BIKE 密钥封装的位操作计算结果，可以看出，三个推荐参数集的位操作规模显然都达到了NIST 安全强度等级的标准.

表9 BIKE 方案的安全强度等级Table 9 Security strength levels of BIKE

4.2.3 本节小结

本节总结了2 个基于编码问题的密码方案，分别为Classic McEliece 和BIKE，其中BIKE 是McEliece 的变体.这两个方案同样有较为完善的参数集，以适应不同的安全强度需求.但基于编码问题的方案往往在效率上不如基于格的方案，难以同时满足短密文、短密钥和短加密时间，因此在实际可用性的提升上，基于编码的密码方案还有很大的研究空间.

4.3 基于其他抗量子攻击困难问题的密码方案

本节讨论的其他抗量子攻击困难问题主要包括哈希函数寻找碰撞和原像问题、多变量二次映射求解问题和超奇异椭圆曲线同源映射求核问题，分别对应的是基于哈希的密码方案、基于多变量的密码方案和基于同源的密码方案.由于上述三类密码体系对应的安全可行方案并不多，因此在这里合并阐述.

4.3.1 基于哈希的密码方案

目前较为安全可行的基于哈希的后量子密码方案为SPHINCS+，目前入围了NIST 第三轮备选方案.SPHINCS+决定安全性的参数选择包括两方面，一是哈希函数的实例化选择，二是其余的固定参数集.在SPHINCS+的官方文档中，推荐使用SHA-256、SHAKE-256 和Haraka 三类函数族对方案进行实例化.

在第三轮的提交中，SPHINCS+提供了三种不同的哈希族，并给出了6 种不同的参数集以适应三种安全等级[59]，其中以“s” 结尾的变体具有更小的密钥和密文，“f” 结尾的变体具有更快的运行速度，n为安全参数，w为Winternitz 系数，h为超树(hypertree) 的高度，d为超树的层数，k为随机子集森林(forest of random subsets，FORS) 中树的数量，t为每棵树中叶子的数量，其安全强度等级见表10(注: 当哈希函数使用Haraka 时，最高安全等级为Category 2).由于SPHINCS+的密码分析算法往往是针对底层哈希函数展开的，因此不同的实例化选项会导致不同的安全强度，故表10 不列举经典门电路规模这一指标.

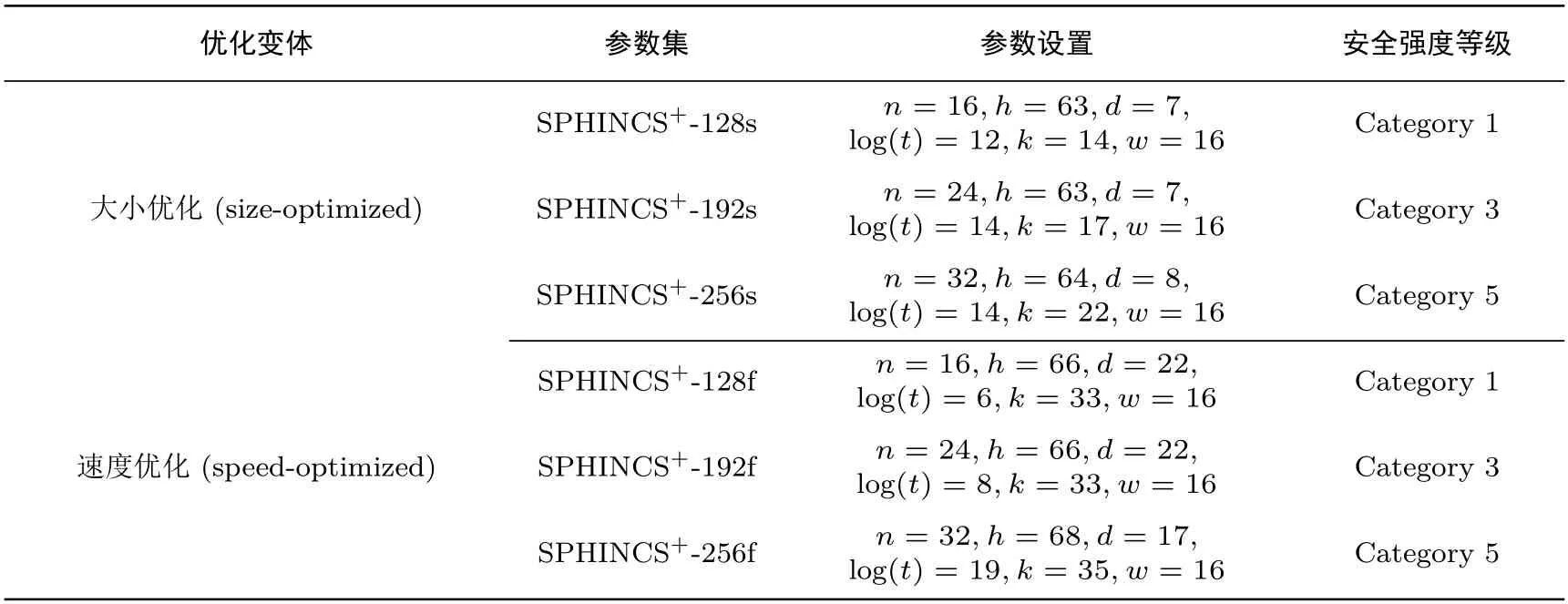
表10 SPHINCS+ 方案的安全强度等级Table 10 Security strength levels of SPHINCS+

4.3.2 基于多变量的密码方案

多变量二次映射(multivariable quadratic mapping，MQ mapping) 的求解问题是指给定一个有限域上的多变量二次映射P:→和一个目标值，找出一个值，使得P(s)t.此问题对于量子计算机而言是难解的.

根据UOV 结构生成的最具代表性的方案就是Rainbow 签名方案，该方案已经入围NIST 第三轮的正式候选方案.

Rainbow 具有一种标准方案和两种变体方案CZ-Rainbow[61]和compressed Rainbow，三个方案对于Category 1/3/5 各提出了一组参数集以适应其安全性[62].值得注意的是，虽然Rainbow 方案提交的安全性看似十分完备，但近期有研究提出对于Rainbow 在NIST 标准化第二轮提出的SL1 参数集，可使用标准笔记本电脑耗时约53 小时完成密钥恢复攻击[63]，而对于第三轮的SL1 参数集，提供高28倍的成本也可攻破.目前Rainbow 方案的提出者给出的应对方案是将原先满足Category 3 的参数集用于Category 1，Category 5 的参数集用于Category 3，因此，目前最高的安全等级是空置的[64].

表11 给出的是经修改后Category 1 和Category 3 等级对应的方案参数，其中F 为指定的有限域，oi和vi分别为油变量和醋变量的数量.攻击Rainbow 方案所需的经典门电路规模使用的是文献[63] 给出的最新实验结果，可以看出，原本适配Category 3 和Category 5 的参数，目前只能符合Category 1 和Category 3 的安全性要求.

表11 Rainbow 方案的安全强度等级Table 11 Security strength levels of Rainbow

4.3.3 基于同源的密码方案

基于同源的密码方案主要是基于超奇异椭圆曲线同源的Diffie-Hellman 框架(supersingular isogenybased Diffie-Hellman，SIDH) 构建的[65].该框架的安全性依赖于le-同源困难问题，指给定两条椭圆曲线E1和E2，曲线之间存在核大小为le的同构映射Φ，求解映射的核.该问题对于量子计算机而言仍然是困难的.较为典型的基于同源的密码方案为SIKE 方案，该方案可用于密钥封装，目前已入围NIST 标准化第三轮的备选方案.

SIKE 方案主要的公开参数有: 定义椭圆曲线所在有限域的e2和e3，其中p-1;初始椭圆曲线E0/;对应点的一组三个x 坐标;对应点E0的一组三个x 坐标.由于参数庞大，在此不做赘述，仅给出参数集名称、主要安全参数设置和安全强度等级.

SIKE 针对三类不同的安全等级，分别提出了3 组参数集SIKEp434、SIKEp610 和SIKEp751 以适应安全性[66]，其中p434/p610/p751 指代的是椭圆曲线所在的有限域为//，具体取值见表12.

表12 SIKE 方案的安全强度等级Table 12 Security strength levels of SIKE

但根据最新的研究，已有密码分析算法能在单核CPU 上，用62 分钟恢复SIKEp434 参数，对于SIKEp610 和SIKEp751，可以在8 小时15 分钟和21 小时37 分钟内恢复密钥[67].这使得SIKE 这一进入NIST 后量子第四轮终选的密码算法的安全性受到了极大的冲击，SIDH 这一问题的困难性也受到了质疑.在作者进一步修订方案参数之前，本文仍然采用了其说明文档中阐述的方案参数.由于文献[67] 还未在完整版研究中给出密码分析算法的复杂度，因此，在此暂不介绍攻击SIKE 的经典门电路规模.

4.3.4 本节小结

本节总结了基于哈希、多变量和同源的密码方案，包括 SPHINCS+、Rainbow 和 SIKE，其中SPHINCS+已经入选NIST 后量子标准化最终确定方案名单，也是名单内唯一一个非格密码的方案.从整体而言，基于这三类问题的稳定方案都较少，在3 年内被证明稳定可用的方案也在近期被不同程度地攻破.一方面，这给了研究者更大的研究和突破空间，但另一方面，从应用的角度，这几类方案目前还不适合被用于大范围的加密和签名应用中，一旦出现安全问题，则后果无法估量.

5 商用安全服务的密码安全强度分析

本节将讨论目前国内外企业使用的安全服务方案中，公钥密码方案的应用及其安全强度评估.分析将分为经典公钥和后量子公钥的应用两部分展开.

5.1 经典公钥密码方案的安全应用

在目前的安全服务应用中，经典公钥密码方案通常被用于密钥封装和数字签名，数据加密的任务通常由对称密码完成.而在经典公钥密码方案中，使用最多的方案为基于大整数分解的RSA 方案和椭圆曲线上的各加密和签名方案.经典公钥密码方案目前已被广泛用于国内外企业的安全服务中，如谷歌云密钥管理服务、微软的Azure 信息保护服务、阿里云的数据加密和密钥管理服务等，其总体应用情况如表13 所示.

表13 部分经典公钥安全服务的安全强度Table 13 Security strength of some classical public key security services

5.1.1 谷歌

谷歌云密钥管理服务(cloud key management service，cloud KMS) 使用BoringSSL 实现中的BoringCrypto 模块(BCM) 进行所有相关的加密工作，该模块涵盖的最新算法包括RSA-2048、RSA-3072、RSA-4096、EC-P256 和EC-P384 几种公钥密码方案[68].

Cloud KMS 椭圆曲线数字签名可选用P256 和P384 曲线的ECDSA 算法，分别具有128 和192 位安全强度.Cloud KMS 的RSA 加密和签名均可选用模数长度为2048、3072、4096 位的RSA 算法，分别具有112、128 和149 (根据公式(1)近似) 的安全强度.Cloud KMS 密钥封装方案可使用3072 和4096位的RSA[69]，分别具有128 和149 位的安全强度.

5.1.2 微软

微软在安全开发生命周期密码建议中也对公钥密码使用的安全性有相似的规定[70]: RSA 的模数长度不少于2048 位，ECDSA 和ECDH 的密钥长度不少于256 位(即使用P-256、P-384 和P-521 三种曲线)，整数域上的DH 算法公钥长度不少于2048 位，即整数DH 和RSA 的安全强度不少于112 位，椭圆曲线方案的安全强度不少于128 位.

在具体的安全服务中，如Azure Right Management Service 中，使用了2048 位的RSA 算法来保护对称密钥，具有112 位的安全强度[71].

5.1.3 阿里巴巴

阿里云数据加密服务使用PKCS #11[72]支持数据加密服务，该服务支持的公钥密码算法有RSA-1024、RSA-2048、RSA-3072、RSA-4096 和ECDSA (P-224、P-256、P-384、P-521).RSA 算法可用于密钥生成、密钥封装、加密和签名，使用P-256、P-384 曲线的ECDSA 算法可用于密钥生成和签名，其余曲线仅可用于密钥生成[73].因此，公钥加密方案的密钥封装和加密安全强度在112～149 位范围内，签名的安全强度在112～192 位范围内.

阿里云密钥管理服务支持的非对称算法子类包括RSA、ECC 和SM2 三种，其中RSA 和SM2 同时支持加、解密和签名、验签，ECC 仅支持签名、验签[74]，SM2 仅在国内的托管机上支持服务.RSA 算法的密钥规格有RSA-2048 和RSA-3072，ECC 算法的密钥规格有EC-P256 和EC-P256K，SM2 算法的密钥规格有EC-SM2[75].因此，RSA 可提供112～128 位的安全强度，ECC 可提供128 位的安全强度，SM2 可提供128 位的安全强度(SM2 采用的是256 位ECC 中的一种曲线[33]).

5.2 后量子公钥密码方案的若干尝试

后量子公钥密码方案在商用安全服务中的应用则相当有限.在可以查阅到的方案应用中，大多数服务是在签名和密钥封装中试验性地引入NTRU-HRSS、CRYSTAL-KYBER、Rainbow、SIKE、BIKE 等方案，并根据研究的跟进不断调整方案的使用与否.

目前国内的安全服务对于后量子公钥的正式应用较少，且文档和代码的开源进度和意愿均不强烈，因此，本节将更多聚焦于海外企业的安全服务中的后量子公钥密码方案及其安全性，其总体发展情况如表14 所示.

表14 部分后量子公钥安全服务的安全强度Table 14 Security strength of some post-quantum public key security services

5.2.1 Cloudflare

CIRCL 是Cloudflare 于2019 年发布的Go 语言密码库[76]，目前已投入使用，其中包含了一系列后量子加密算法.

CIRCL 的后量子密钥封装算法使用了SIKE (p434，p503，p751)、CSIDH[77]、KYBER (512，768，1024)，其中SIKE 和KYBER 可提供1、3、5 级的安全强度，CSIDH (512，1024，1792) 可提供1、2、3 级的安全强度.CIRCL 的后量子公钥密码算法使用的是KYBER，同样可提供1、3、5 级的安全强度.CIRCL 的后量子数字签名算法使用的是DILITHIUM，可提供2、3、5 级的安全强度.

同时，Cloudflare 在2019 年还联合Google Chrome 进行TLS 后量子实验计划，将现有的后量子方案应用于TLS 连接协议中[78].该实验计划将SIKE (p434) 和NTRU-HRSS-SXY[79]结合目前最常用的密钥交换算法X25519、SIKE 和HRSS-SXY 都可提供1 级的安全强度.实验表明，HRSS 在未来更有可能被用于TLS 中.

5.2.2 谷歌

谷歌在 2016—2018 年进行了面向 Chrome 浏览器 TLS 协议的两轮后量子实验 CECPQ1 和CECPQ2.其中CECPQ1 使用的是NewHope (1024) 方案[80]，可提供5 级的安全强度.CECPQ1的实验结果并不出色，其产生的连接延迟十分明显.随后，谷歌又发布了CECPQ2 实验，使用了NTRUHRSS-SXY 进行密钥封装的辅助，该方案可提供1 级安全强度.该实验随后被CECPQ2b 替代，即上文中将SIKE (p434) 应用于TLS 的实验.

5.2.3 亚马逊

在2020 年，亚马逊AWS 密钥管理服务的混合密钥封装也引入了后量子密钥交换方案，包括KYBER(512)、BIKE (L1，L3，L5)、SIKE (p434，p503，p610，p751) 三个方案[81]，其中KYBER 可提供1 级的安全强度，BIKE 可提供1、3、5 级的安全强度，SIKE 可提供1、2、3、5 级的安全强度.

6 总结与讨论

本文主要针对目前常见的经典公钥密码方案和后量子公钥密码方案各参数集的安全性进行了定量分析.结果显示，目前经典公钥体系已有了完善的由80 位至256 位的安全等级，并至少满足未来至少十年的应用需求.但值得注意的是，量子计算机的发展已开始对经典公钥体系的安全性产生冲击，若量子密码分析算法在未来出现了突破性的进展，目前的经典公钥体系将面临着更严峻的挑战，针对上述可能存在的隐患，各大安全服务提供商也应把经典公钥密码方案使用的调整和过渡提上日程，以防未来产生较大的安全波动.

目前后量子公钥密码体系相关研究也在如火如荼地进行，按照NIST 标准化的要求，绝大多数方案可匹配至安全等级1/3/5 级.总体看来，后量子公钥密码方案安全性和实用性仍需要继续提升，以满足更多的实际应用需求.首先，后量子密码方案的密码分析相关研究还很不成熟，故其给出的安全强度等级的结论并不稳固，如最近出现安全等级调整的Rainbow 方案.随着NIST 标准化选拔和学界研究的进一步深入，希望这样的问题可以得到一定程度的解决.其次，目前相对高效且安全的标准化后量子公钥密码方案大多为基于格的方案，基于其他困难问题的方案往往很难同时满足高效性和较为稳定的安全性，每个安全等级内可选择的参数集都相对较少，需要进一步探索和研究.

在应用上，目前后量子公钥在安全服务中的使用还是较为局限的，或缺乏公开文档资料，或仍处于试验阶段.特别是在各大企业对TLS 的后量子化的实践中，其安全性和性能的协调始终是一大问题，且后量子方案多是以混合使用的方式出现，而非独立使用，这也使后量子方案的安全性不能被充分地应用，特别是在受到可能的量子攻击时.实现更多独立、安全、高效的后量子化应用，也会是未来公钥密码应用可研究的方向.