基于VMD和改进DenseNet的滚动轴承故障诊断

董路南, 邓艾东, 范永胜, 刘 洋

(1. 东南大学 能源与环境学院, 南京 210096; 2． 大型发电装备安全运行与智能测控国家工程研究中心, 南京 210096; 3. 国家能源集团江苏电力有限公司, 南京 215433)

随着科学技术的不断发展,机械设备成为许多生产过程中的关键部件,而旋转机械设备对于制造业的发展十分重要[1]。风电机组滚动轴承是大型旋转机械的关键部件,在设备运行过程中,滚动轴承承受巨大的载荷,容易发生故障。资料显示,在旋转机械故障中40%以上是轴承故障,其运行状况影响着整机性能[2],会对安全运行造成巨大影响。因此,有必要对滚动轴承进行故障诊断,提前发现异常并进行调整,从而预防事故发生[3-5]。

滚动轴承故障诊断方法已经有了一定发展,但目前存在2个主要问题:(1) 需要人为提取传统特征,针对不同工况下的故障需要提取不同的特征,这将会需要更多的专家经验[6];(2) 在强噪声、变工况条件下故障特征难以提取,无法有效完成滚动轴承故障诊断。

可采用深度学习来进行滚动轴承故障诊断,其可以减少对于专家经验的依赖,无需人工提取故障特征,因此在旋转机械故障诊断中得到越来越多的应用[7-10]。但是,传统的深度学习鲁棒性差,容易出现梯度消失,在强噪声下准确率不高。为此,一些研究者从数据和算法两方面,提出了抵抗噪声干扰效果较好的模型。李涛等[11]使用自编码对信号进行降噪,然后输入到卷积神经网络完成故障诊断,但过程中需要训练2个模型。文献[12]～文献[15]提出了具有一定抗噪性能的模型,不用对数据进行处理,但是能实现的最低信噪比为0 dB,对于低于0 dB的强噪声诊断效果较差。

综上所述,传统的卷积神经网络只能利用单一特征,无法提取振动信号更深层次的特征,导致诊断效率不高。结合自编码模型后,虽然能够有效实现故障诊断,但是需要训练2个模型,诊断时间过长。此外,其他传统深度学习模型在信噪比低于0 dB的强噪声环境下,诊断效果较差。

针对上述问题,笔者提出一种基于变分模态分解(VMD)和改进的稠密连接网络(DenseNet)模型。VMD能够将振动信号按照频率进行划分,通过相关系数法筛选出相关性最小的本征模态分量(IMF),再将其余模态分量重构,实现信号的初步降噪。DenseNet网络首先利用“卷积+池化”单元提取多维特征,再引入通道注意力机制使模型更关注具有区分度的特征,从而加强模型特征提取能力,然后利用多个DenseBlock块实现特征重用,加强了特征的传递,从而提取更多的有效特征。同时其训练参数更少,有效缓解了梯度消失问题,从而更高效地实现滚动轴承故障诊断。

1 理论介绍

1.1 变分模态分解

变分模态分解是一种基于经典维纳滤波和希尔伯特变换的自适应和完全非递归的模态变分和信号处理方法。该方法的优点是可以确定模态分解的个数,自适应性表现为可以根据实际情况确定模态分解的个数、最佳中心频率和有限带宽,分解之后得到的固有模态分量可以将原始信号按照频域进行有效划分。变分模态分解的核心思想是构建和求解变分问题。

变分问题的约束条件为所有模态之和与原始信号相同。变分模型如下:

(1)

式中:uk为各模态分量;ωk为各模态分量的中心频率;δ(t)为脉冲函数;k为模态数;f为原始信号;t为时间。

求解变分问题,引入拉格朗日乘子λ和二次惩罚因子α,将构造的变分模型转化为无约束变分求解问题,拉格朗日函数L({uk},{ωk},λ)如下:

(2)

(3)

(4)

拉格朗日算子更新公式如下:

(5)

当满足式(6),则停止迭代:

(6)

其中,当ε为10-7时计算结束。

1.2 稠密链接网络

为了更好地进行特征提取,深度网络需要不断增加网络深度。但是,随着深度神经网络层数的不断增加,会出现梯度消失或者爆炸等情况,阻碍了深度神经网络的发展。DenseNet网络突破了传统思维,不再使用加深网络层数和加宽网络结构的方式,而是从特征的角度出发,采用特征重用和旁路的设置,以前面所有层的输出作为输入。同时网络更窄,这样可以大大减少网络参数,有效避免梯度消失的产生。

DenseBlock和Transitionlayer是DenseNet的重要部分。

(1) DenseBlock

DenseBlock作为DenseNet的核心组成部分,其结构如图1所示。DenseBlock在层之间的计算公式如下:

xl=Hl([x0,x1,x2,…,xl-1])

(7)

式中:xl为第l层网络的输出;x0,x1,…,xl-1为各个输入层的输入;Hl为非线性变换函数,是一种组合运算,包括BN+Relu+1×1Conv+BN+Relu+3×3Conv。

DenseBlock中还有一个重要参数K,称为增长率(GrowthRate)。假设输入特征图的通道数为K0,那么第l层的通道数就变成K0+(l-1)K。从第二层开始,每一层都会按照设定的增长率增加通道数,然后和前一层进行拼接。

(2) Transitionlayer

经过DenseBlock层之后,输出特征图像的维度会急剧增加。因此,在2个DenseBlock之间增加Transitionlayer,传导层是由1×1卷积和2×2的AvgPool组成。其中,1×1的卷积层在提取特征的同时可以减少通道数量,具有压缩模型的作用,池化层可以对提取的特征图进行降维。

1.3 通道注意力机制(CAM)

当滚动轴承出现故障时,局部故障源和健康部位冲击产生振动,不同部位发生故障产生的振动信号不完全相同,为了增大不同故障的区分度,引入通道注意力机制。

加入通道注意力机制可以对不同特征赋予不同的权重,故障特征的权重更大,使得模型更加关注故障特征,从而增强了模型的诊断性能。模型如图2所示。

图2 通道注意力机制Fig.2 Channel attention mechanism

设输入通道注意力机制的矩阵为X∈RH×1×W,其中H为通道数,W为数据长度。中间向量c∈RH/R×1×1,R为通道压缩量。2个挤压-激励网络输出结果相加得到新的特征向量c′=RH×1×1。通道注意力机制输出矩阵C为:

C=X·σ(c′)

(8)

其中,σ表示sigmoid函数。

2 实验模型

所提出的模型为VMD和改进的DenseNet,该模型以加噪声的振动信号作为输入,首先经过VMD分解,根据经验选取K=4,α=2 000,然后根据相关系数筛选出相关性较大的3个模态分量,将这些模态进行重构。再将重构信号转化为二维图像,最后将二维图像送入DenseNet网络。

DenseNet网络首先经过一个“卷积+池化”单元,用来提取多维特征。然后增加一个通道注意力机制使模型更加关注具有区分度的特征,从而加强模型特征提取能力。再分别经过DenseBlock、Transitionlayer、AvgPool和Softmax等结构完成故障诊断。模型结构如图3所示,模型具体参数见表1。

图3 VMD和改进DenseNet模型Fig.3 VMD and improved DenseNet model

表1 模型结构参数Tab.1 Structural parameters of the model

3 实验分析

3.1 数据集

为了验证所提模型的有效性,实验采用凯斯西储大学(CWRU)滚动轴承振动数据集。该试验台是由1.5 kW的电动机和功率计组成,轴承包括驱动端和风扇端,驱动端轴承型号为SKF-6205,其采样频率为12 kHz,转速为1 797 r/min,包括0 hp、1 hp、2 hp和3 hp 4种负载(1 hp=735.499 W)。轴承数据包括正常数据、内圈故障数据、外圈故障数据和滚动体故障数据4种类型。每种故障数据又包括3种尺寸:0.007 in、0.014 in和0.021 in(1 in=2.54 cm)。最终轴承数据分为10种,包括9种故障数据和1种正常数据。

为避免数据过少导致模型出现过拟合,采取数据重叠分割的方法进行数据增强。从正常数据起始点开始采集,每次采集1 024个点,采集结束后向后移动200个点继续采集,最终共6 000个样本。其中,4 500个样本划分为训练集,1 500个样本划分为测试集。创建数据集见表2。

3.2 模型参数

实验在pytorch深度学习框架下进行,训练前将数据集划分为训练集、验证集和测试集,比例分别为65%、10%和25%。epoch取100,learningrate为0.001,损失函数选用交叉熵损失函数,DenseNet网络输入的图像尺寸为32×32。

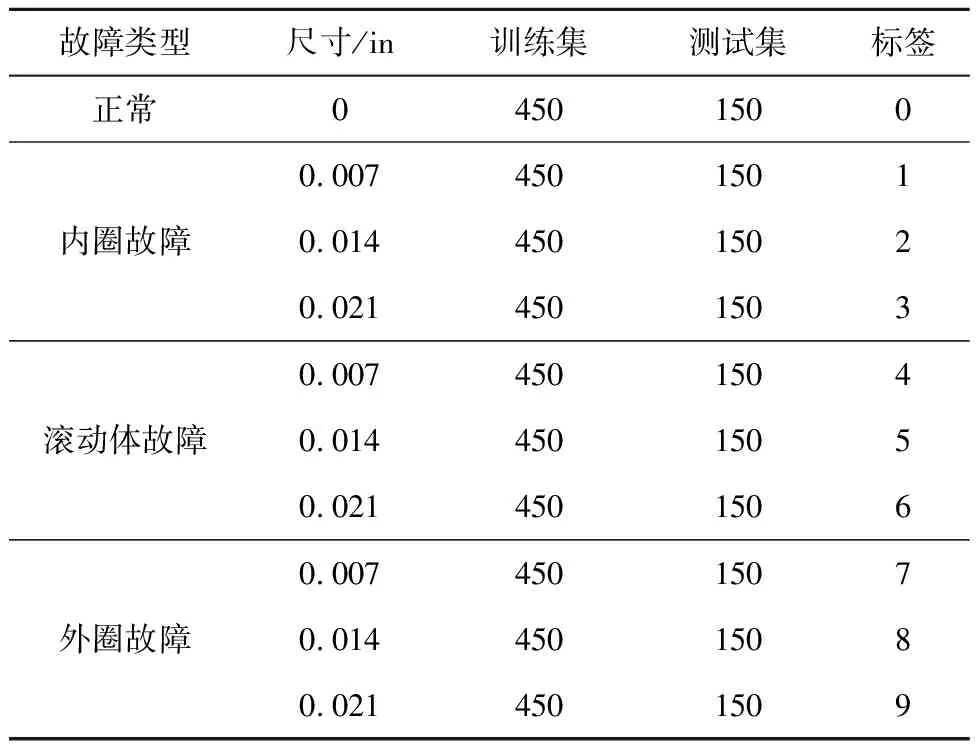
表2 实验数据汇总

网络模型中DenseBlock数量选取为3。在相同实验数据下对比数量不同的Denselayer对诊断准确率的影响。当Denselayer取1时准确率为98.53%;取2时,准确率为99.60%;取3时,准确率为96.60%。因此,最终确定本文模型中的Denselayer数量为2。

3.3 实验结果对比

CWRU滚动轴承振动数据是在试验环境中进行的,与实际工业场景相比缺少了噪声干扰。为了还原真实的工业环境,加入一定信噪比(S)的白噪声来验证所提方法的有效性。信噪比是衡量信号中所含噪声大小的重要指标,计算公式如下:

(9)

式中:Psignal为信号功率;Pnoise为噪声功率。

3.3.1 VMD降噪

当原始振动信号加入一定信噪比的噪声后,原始信号的特征信息会被噪声淹没,这将会加大故障诊断的难度。笔者将正常状态的轴承原始振动信号加入信噪比为-4 dB的噪声信号,然后经过VMD分解进行降噪。降噪过程如图4所示。

从图4可以看出,加入噪声后,原始振动信号完全被淹没,只能看到均匀的噪声信号。经过VMD分解,选取相关性较高的IMF,然后重构信号。从图4可以看出,VMD分解后噪声信号明显减少,表明了VMD在降噪方面的优势。

3.3.2 模型诊断准确率对比

采用CWRU轴承数据集,选用0 hp负载数据。加入-4 dB信噪比的噪声进行分析,在相同数据集下将对比分析本文模型、胶囊网络与卷积神经网络(FD-CNN)[16]、基于多层降噪技术及改进卷积神经网络(ICNN)[17]、CNN、VMD-CNN和VMD-DenseNet。不同模型的诊断准确率如图5所示。

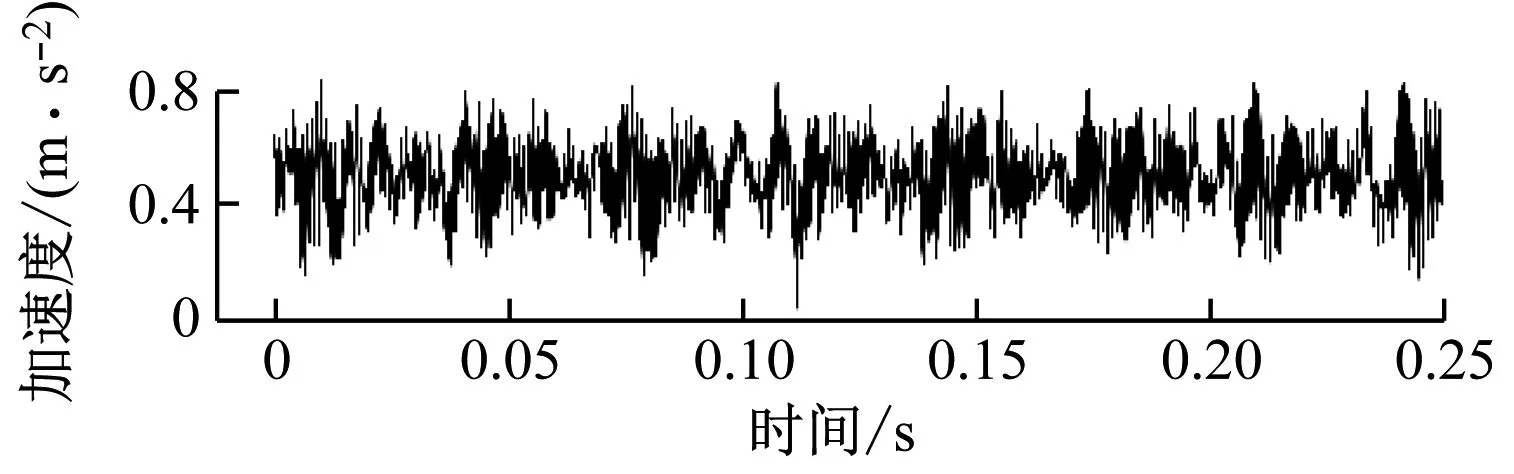
(a) 正常状态

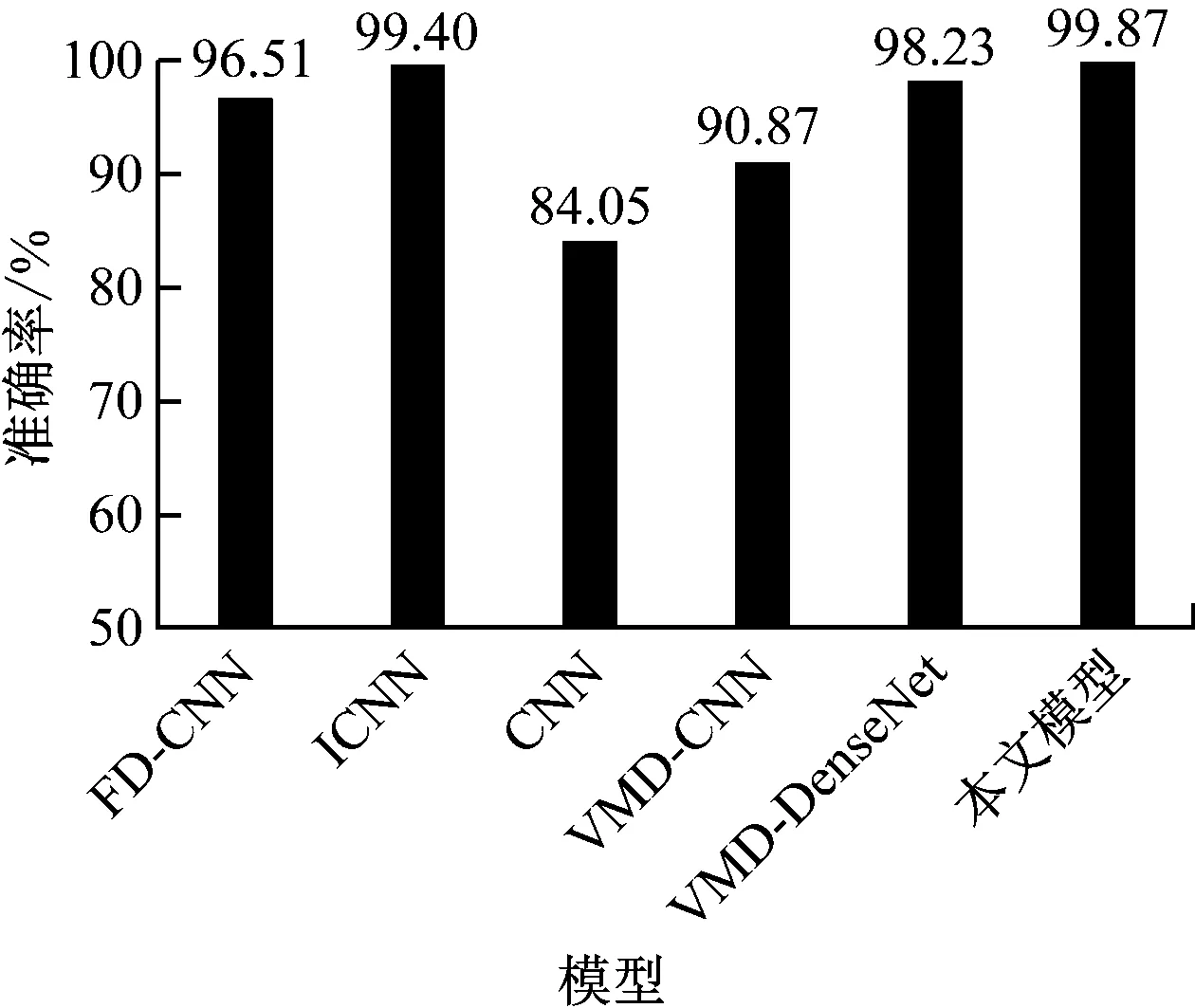
图5 诊断准确率对比Fig.5 Comparison of diagnostic accuracy

由图5可知,在S=-4 dB环境下,CNN模型的诊断准确率为84.05%,效果较差;VMD-CNN模型的诊断准确率有所提升,体现了VMD在降噪方面的优势;与CNN模型相比,FD-CNN和ICNN模型的诊断准确率分别提升12.46%和15.35%;VMD-DenseNet模型的诊断准确率相对较高,体现了DenseNet网络的优越性;本文模型诊断准确率最高,为99.87%,说明通过VMD初步降噪,结合DenseNet强大的特征提取能力,并引入通道注意力机制,能够更高效地实现强噪声下的滚动轴承故障诊断。

3.3.3 模型抗噪性能分析

为了进一步验证所提模型的优越性,改变噪声大小,在-10～10 dB噪声范围内验证本文模型的抗噪性。由于ICNN、VMD-DenseNet及本文模型的诊断准确率相对较高,因此,对这3种模型进行比较,结果如图6所示。

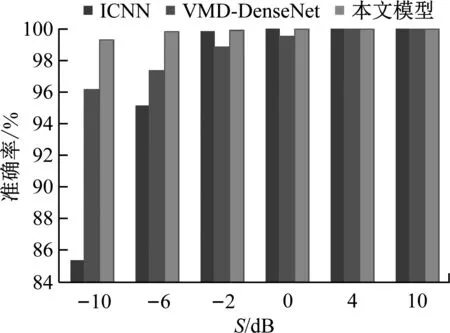
图6 不同噪声下的模型准确率Fig.6 Model accuracy under different noise

由图6可知,信噪比为-10 dB时,VMD-DenseNet模型和ICNN模型的诊断准确率分别为96.17%和85.39%,本文模型准确率为99.27%;信噪比为-6 dB时,ICNN模型和VMD-DenseNet模型的诊断准确率分别为95.17%和97.35%,本文模型诊断准确率为99.80%;随着信噪比的不断增加,诊断准确率主要取决于模型自身特征提取的能力,各模型的诊断准确率逐渐趋近于100%。因此,本文模型在不同信噪比的噪声下均具有更好的诊断性能。

3.3.4 训练过程分析

为了分析本文模型的训练情况与性能,图7给出了模型诊断准确率和损失函数在训练过程中的变化情况。

由图7(a)可以看出,迭代次数为20时,模型准确率已达97%,迭代次数为80时,模型完成收敛,准确率到达稳定。由图7(b)可以看出,损失函数下降很快,迭代次数为20时,损失函数已下降到很低,迭代次数为80时模型基本达到稳定,说明模型训练过程较为稳定。

3.3.5 诊断结果分析

为进一步分析本文模型在10种不同类别下的预测准确率,图8为本文模型在信噪比为-4 dB时的诊断准确率混淆矩阵。其中,“Normal”代表正常状态;“B007”代表故障尺寸为0.007 in的滚动体故障;“IR”、“OR”分别代表内圈和外圈故障。

从图8可以看出,在“Normal”等8种类别下的诊断准确率达到了100%,而在“B014”和“IR021”2种类别下出现了错误,诊断准确率为99%。

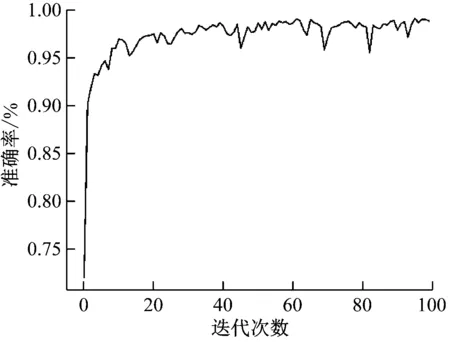
(a) 诊断准确率

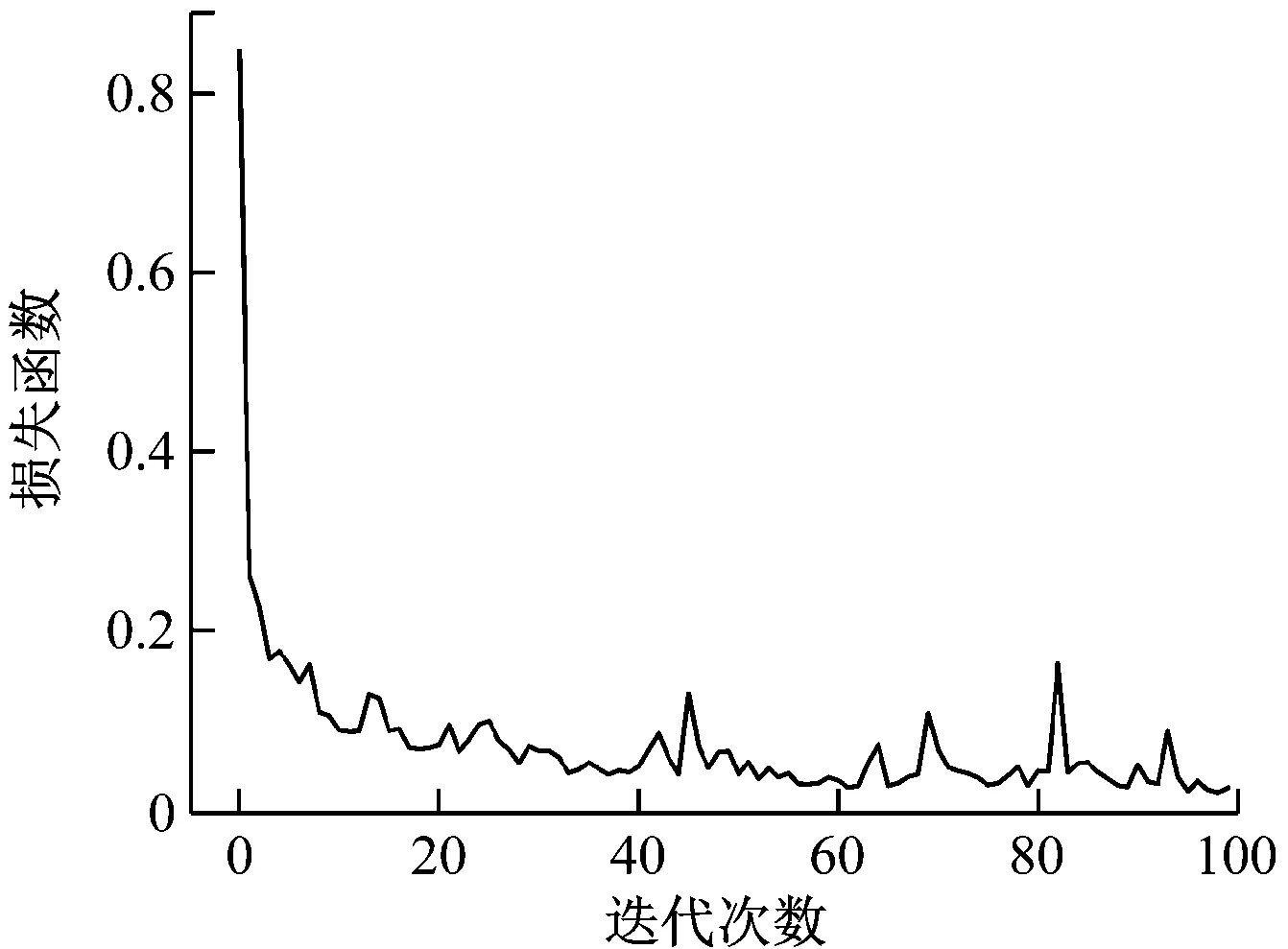
(b) 损失函数图7 训练过程分析Fig.7 Analysis of training process

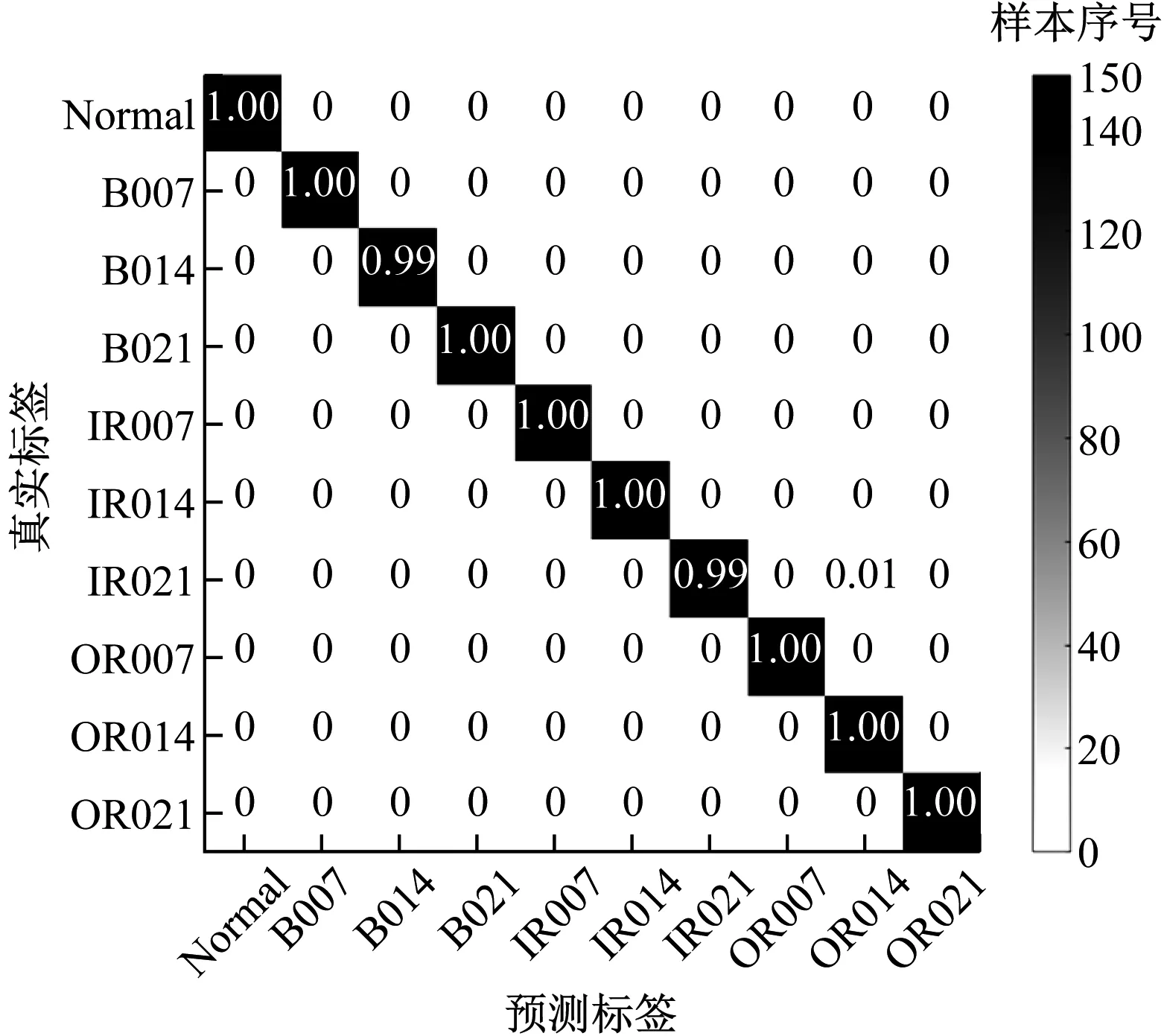
图8 诊断准确率混淆矩阵Fig.8 Diagnostic accuracy confusion matrix

4 结 论

(1) 对比FD-CNN模型、ICNN模型、CNN模型、VMD-CNN模型和VMD-DenseNet模型,本文模型在不同信噪比情况下均具有较高的故障诊断精度,训练过程稳定,收敛速度快,鲁棒性好。

(2) 本文模型在强噪声下的优势主要是利用了VMD降噪、DenseNet网络强大的特征提取能力以及通道注意力机制对故障特征的关注。