基于COMSOL的全陶瓷微封装燃料元件建模与传热分析

王某浩, 步珊珊, 卢绪祥, 刘 瑞

(1．长沙理工大学 能源与动力工程学院,长沙 410114;2．重庆大学 能源与动力工程学院,重庆 400044)

全陶瓷微封装(FCM)燃料因具有优异的热力性能和耐辐照性能等特性,是先进耐事故燃料(ATF)的重要研究内容[1-2]。作为一种弥散型燃料元件,FCM燃料元件结构包括燃料芯块、燃料包壳以及芯块与包壳间气隙,其中燃料芯块由SiC基体和弥散在基体中的TRISO(TRistructural-ISOtopic)燃料颗粒构成。TRISO燃料颗粒自内而外依次为燃料核芯(Kernel)、疏松热解碳(Buffer)层、内致密热解碳(IPyC)层、碳化硅(SiC)层和外致密热解碳(OPyC)层。

FCM燃料芯块结构比较复杂,其内部传热特性通常采用简化模型分析,Brown等[3]采用均质化方法对FCM燃料元件传热温度场进行计算,但该方法忽略了燃料元件的内部结构,因而不能获得详细、精确的温度场分布。近年来随着计算机硬件以及数值技术的快速发展,越来越多的研究者针对精细的燃料芯块结构开展传热分析。刘振海等[4]将TRISO颗粒以六边形形式嵌入基体中并用一定厚度的三维切片构建FCM燃料元件模型,再进行热力计算分析。类似地,Kamalpour等[5]建立六边形晶格分布多区域模型横向切片并进行FCM燃料元件的传热数值分析。Chen等[6]则通过二维纵向切片模型对FCM燃料芯块进行热力分析,计算出压水堆环境下SiC基体的温度分布。实际制造中燃料芯块内部大量TRISO燃料颗粒随机弥散在SiC基体中,而目前大多数研究都对FCM燃料芯块内部燃料颗粒的分布形式进行了简化[3-6],未模拟燃料颗粒随机分布的特征[7-8]。因此需要进一步探索燃料元件内TRISO燃料颗粒随机分布的建模方法,针对三维燃料芯块精细结构内部传热进行计算分析。

笔者提出一种FCM燃料元件内TRISO燃料颗粒随机分布的建模方法,以便更真实地模拟现实应用中FCM燃料元件的几何结构,同时基于该方法构建了全三维FCM燃料元件模型,针对FCM燃料元件内部的传热特性开展计算分析。

1 计算模型与数值方法

1.1 TRISO燃料颗粒随机分布的建模方法

FCM燃料元件的二维结构示意图如图1所示。为了实现TRISO燃料颗粒在FCM燃料芯块内的随机弥散,提出一种FCM燃料元件内TRISO燃料颗粒随机分布的建模方法。其核心思想是首先对FCM燃料芯块分层并将TRISO燃料颗粒小球平均分放在每一层内,随后采用拟物拟人算法[9]使燃料颗粒小球随机分布在各层内,再调整各燃料颗粒小球的轴向位置达到轴向随机分布的效果,最终使TRISO燃料颗粒弥散在FCM燃料芯块内。目前,数值模拟研究采用的TRISO燃料颗粒填充率很多都在40%左右[5-6,10],实际制造过程中为减少燃料颗粒相互接触,一般限制最大允许填充率约为48.3%[11]。经过测试,本文的建模方法可以有效模拟这些较高填充率的颗粒随机分布,能够更好地模拟堆内燃料行为。

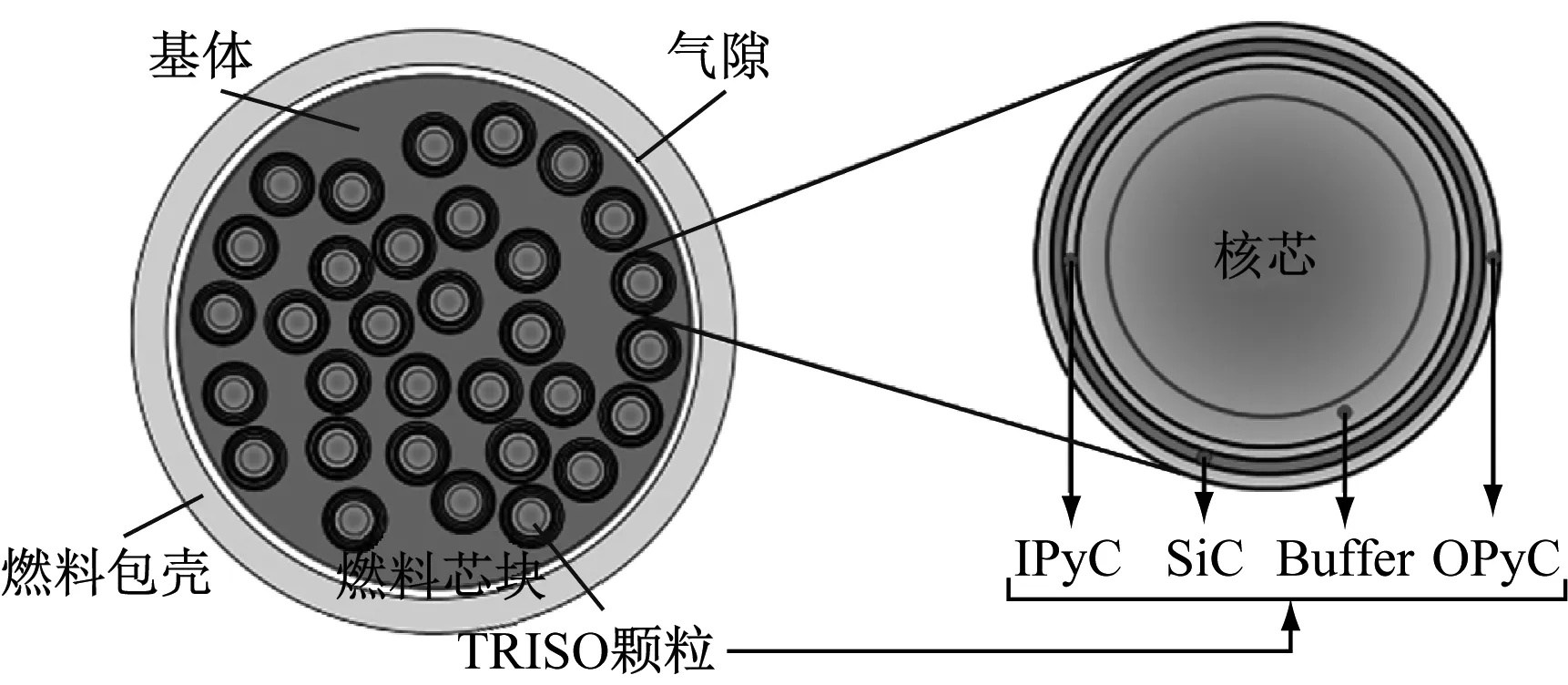
图1 FCM燃料元件的结构示意图Fig.1 Structure diagram of FCM fuel pellet

FCM燃料元件多区域模型构建方法如图2所示。

(1) 如流程一所示,取每一层高度稍大于TRISO燃料颗粒外径,对FCM燃料芯块进行分层并确定各层中心平面位置。

(2) 如流程二所示,确定各层内的TRISO燃料颗粒数目,保证TRISO燃料颗粒球心在所在层中心平面上,然后将各层内TRISO燃料颗粒的随机分布转换为平面等径圆填充的NP(Nondeterministic Polynominal)问题[9],并采用拟物拟人算法求解TRISO燃料颗粒球心的位置。

(3) 如流程三所示,从上层往下层依次将各层TRISO燃料颗粒在轴向可移动范围内随机调整移动,记录各TRISO燃料颗粒位置。

(4) 如流程四所示,根据TRISO燃料颗粒位置以及TRISO燃料颗粒和FCM燃料元件几何尺寸构建模型。

图2 FCM燃料元件多区域模型构建方法流程图

根据以上建模方法及流程,采用有限元软件COMSOL进行建模[12]。模型中TRISO燃料颗粒较多,且每个燃料颗粒又存在包覆层,导致模型结构十分复杂,直接利用COMSOL软件建模难度很大。COMSOL软件中COMSOL LiveLink for MATLAB接口允许用户将COMSOL Multiphysics与MATLAB脚本环境联系起来,从而可实现通过MATLAB脚本文件构建模型。

所研究的TRISO燃料颗粒的物理模型几何参数如表1[13]所示,FCM 燃料元件的物理模型几何参数如表2所示,FCM燃料中TRISO燃料颗粒的填充率为40%。

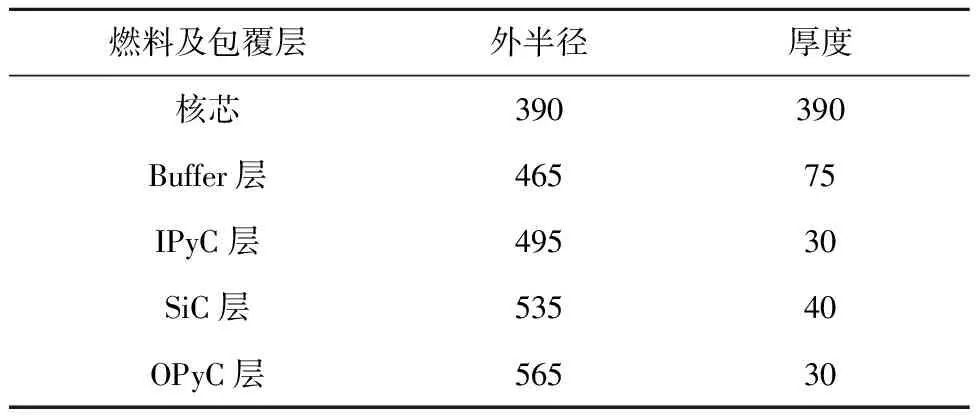
表1 TRISO燃料颗粒物理模型几何参数

表2 FCM燃料元件物理模型几何参数

1.2 控制方程和边界条件

TRISO燃料颗粒和FCM燃料元件的控制方程均为含内热源三维稳态导热微分方程:

(1)

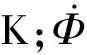
边界条件的设置如图3所示。FCM燃料芯块内部包含随机分布的含内热源的燃料颗粒,FCM燃料元件上下表面为绝热表面,燃料包壳外表面取第三类边界条件,即给定燃料包壳与周围冷却剂间的表面传热系数h及周围冷却剂的温度tf。FCM燃料芯块的平均线功率取315 W/cm[6],h取18 327 W/(m2·K),tf取581.9 K[5]。

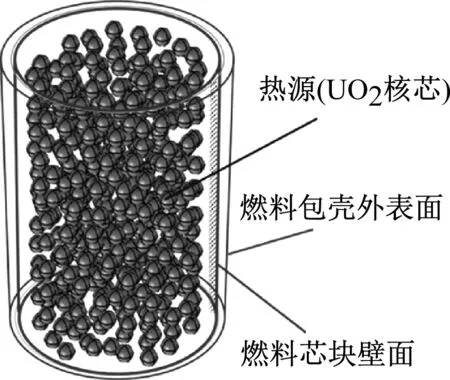
(a) 热源分布

(b) 外边界条件图3 边界条件设置示意图Fig.3 Diagram of boundary condition setting

此外,本文中UO2燃料核芯导热系数由Fink模型[14]得到,SiC层和SiC基体的导热系数由Snead模型[15]得到。其中Fink模型和Snead模型中导热系数随温度的变化如图4所示。TRISO燃料其他包覆层的导热系数参照PARFUME理论手册[16]取值,如表3所示。

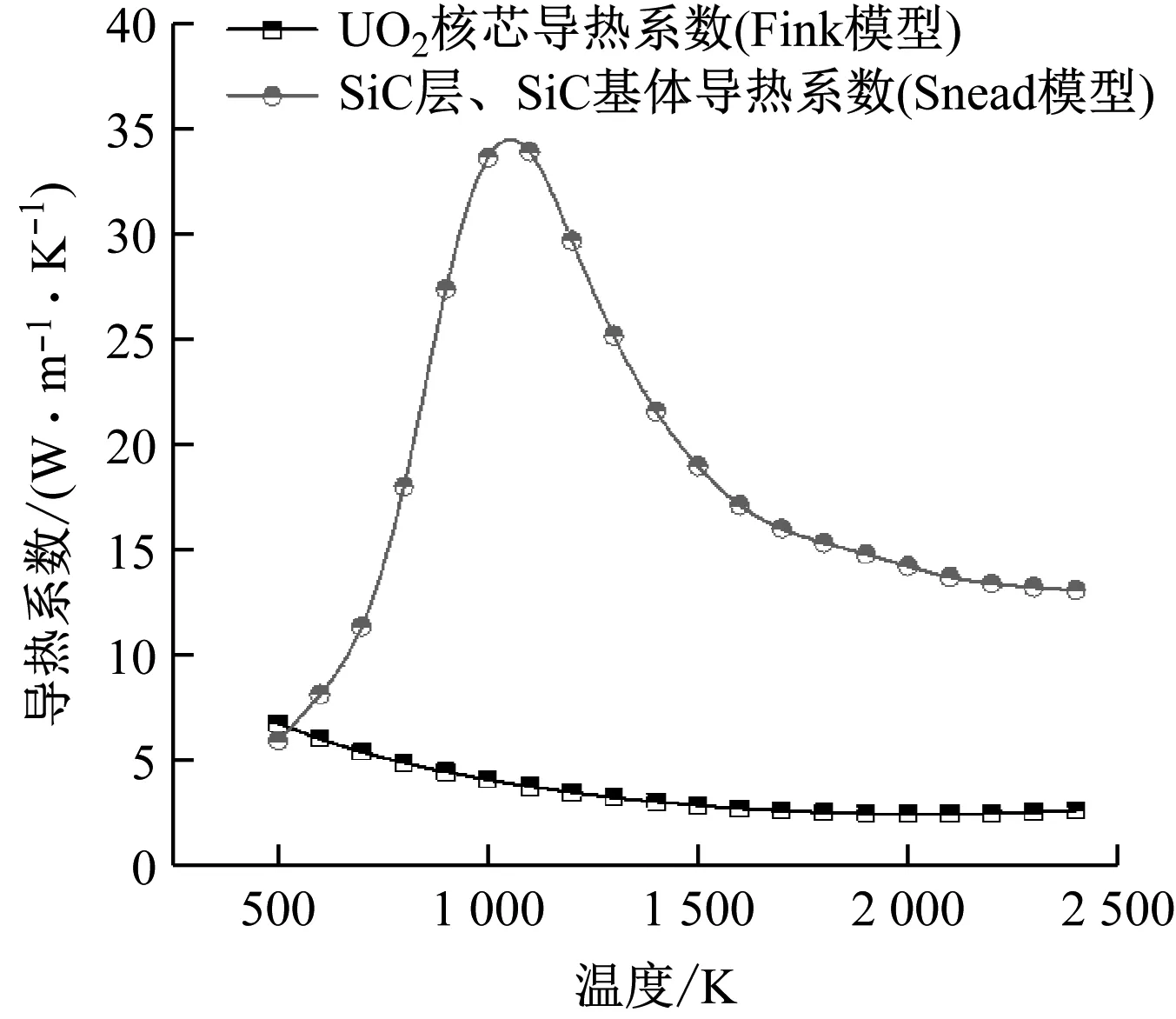
图4 Fink模型和Snead模型中导热系数随温度的变化

1.3 网格独立性分析

选取COMSOL软件自带的粗化、较粗化、常规及细化4种网格单元类型,并结合上述模型及边界条件对FCM燃料元件进行计算。以FCM燃料芯块内最高温度的计算结果为研究对象,将不同网格单元类型计算结果与细化网格单元类型计算结果之间的误差定义为相对误差。表4给出了网格独立性分析的计算结果,可以看出随着网格单元的逐渐细化,网格单元数剧增。当网格单元类型采用粗化网格时,相对误差接近20%,而当网格单元类型取较粗化网格时,相对误差在1%以内。因此最终采用较粗化网格单元类型(网格数量为636 519)进行网格划分,最终网格划分结果如图5所示。

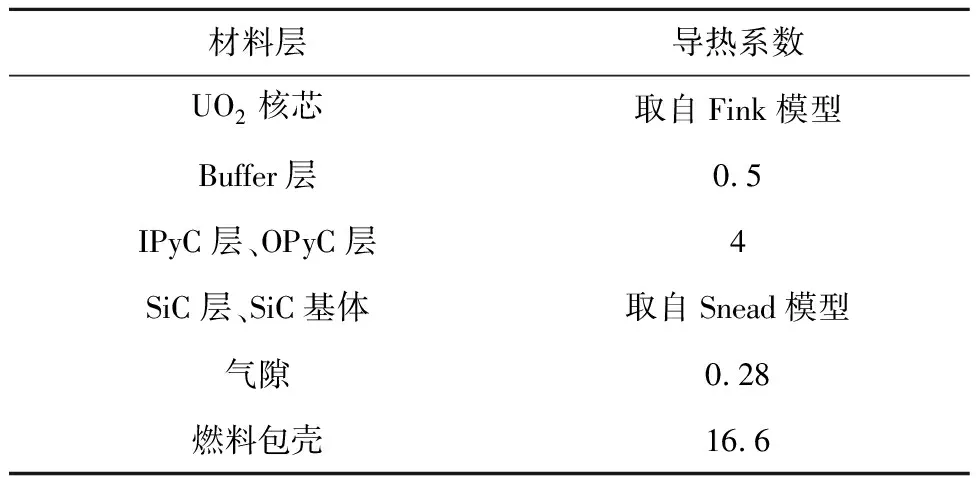
表3 FCM 燃料元件材料的导热系数

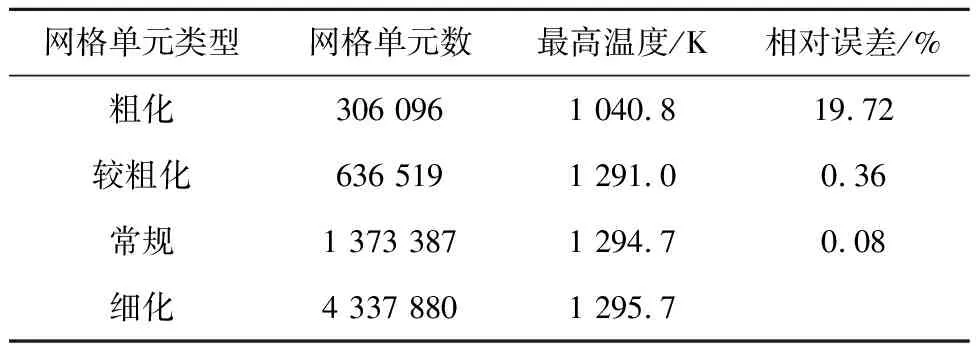
表4 网格独立性分析

(a) 整体网格

(b) 网格细节图5 网格划分结果Fig.5 Results of grid division

1.4 数值方法校核

采用文献[5]的数值模型对本文的数值方法进行校核。其中计算模型为六边形晶格分布的1/6切片式多区域模型,如图6所示。计算工况中燃料元件的平均线功率为2.7×104W/m,h和tf分别为18 327 W/(m2·K)和581.9 K。计算获得的径向温度分布曲线与文献[5]中的径向温度分布曲线对比如图7所示,可以看出数值计算结果与文献[5]的结果均吻合较好,两者的相对误差在1%以内。因此,本文采用的数值计算方法是可靠的。

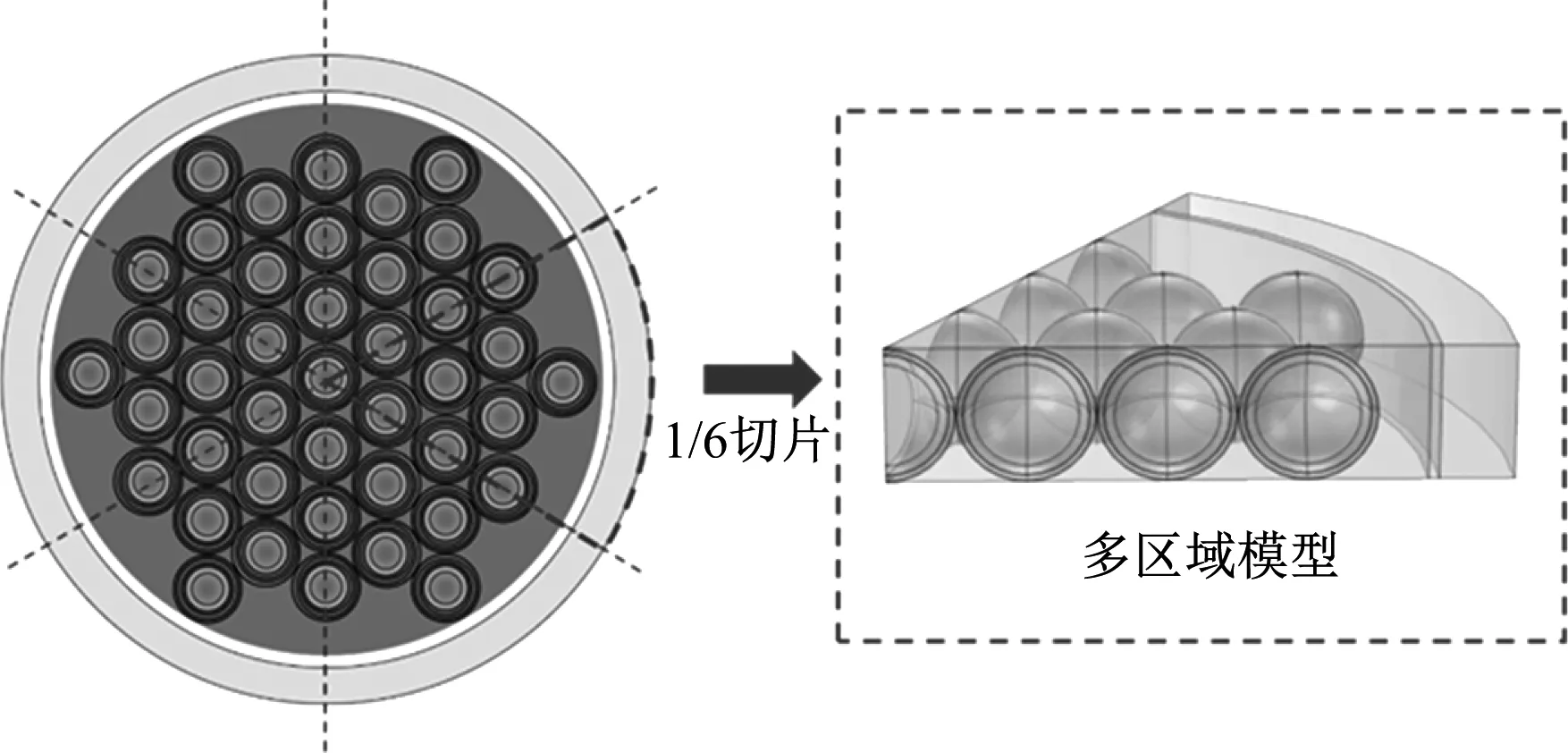
图6 文献[5]采用的几何模型Fig.6 Geometric model used in reference [5]

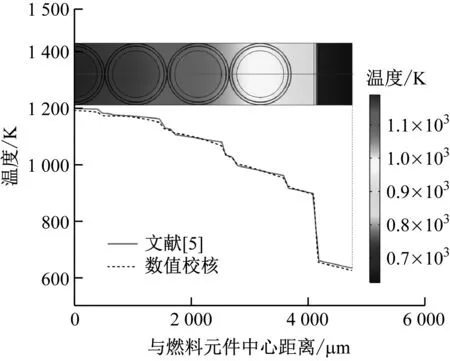
图7 数值方法校核计算结果Fig.7 Checking calculation results by numerical method

2 结果与分析

2.1 40%颗粒填充率下FCM燃料元件的温度场

FCM燃料元件的温度场分布如图8所示,燃料元件中心区域温度最高,沿径向的温度分布总体呈降低趋势:中心区域的最高温度可达1 296 K,而燃料包壳外表面平均温度为639 K。从燃料芯块过渡到燃料包壳过程中,径向温度显著降低,这主要是由于燃料芯块与燃料包壳之间的气隙热阻大导致的。同时TRISO燃料颗粒特别是燃料核芯的温度明显高于周围基体的温度,这与内热源的分布以及燃料颗粒包覆层的传热特性有关。

FCM燃料元件在XZ平面中心线的温度分布如图9(a)所示,TRISO燃料颗粒的温度分布并不对称,这与TRISO燃料颗粒弥散在基体中的具体位置有关。但每个TRISO燃料颗粒的温度分布呈中间高边缘低的趋势。以单个TRISO燃料颗粒为例(见图9(b)),其中心最高温度为1 272 K,右边缘最低温度为1 142 K,并且可以看出这种较大幅度的温差(130 K)变化主要出现在Buffer层,这是由于Buffer层的导热系数较小引起的。

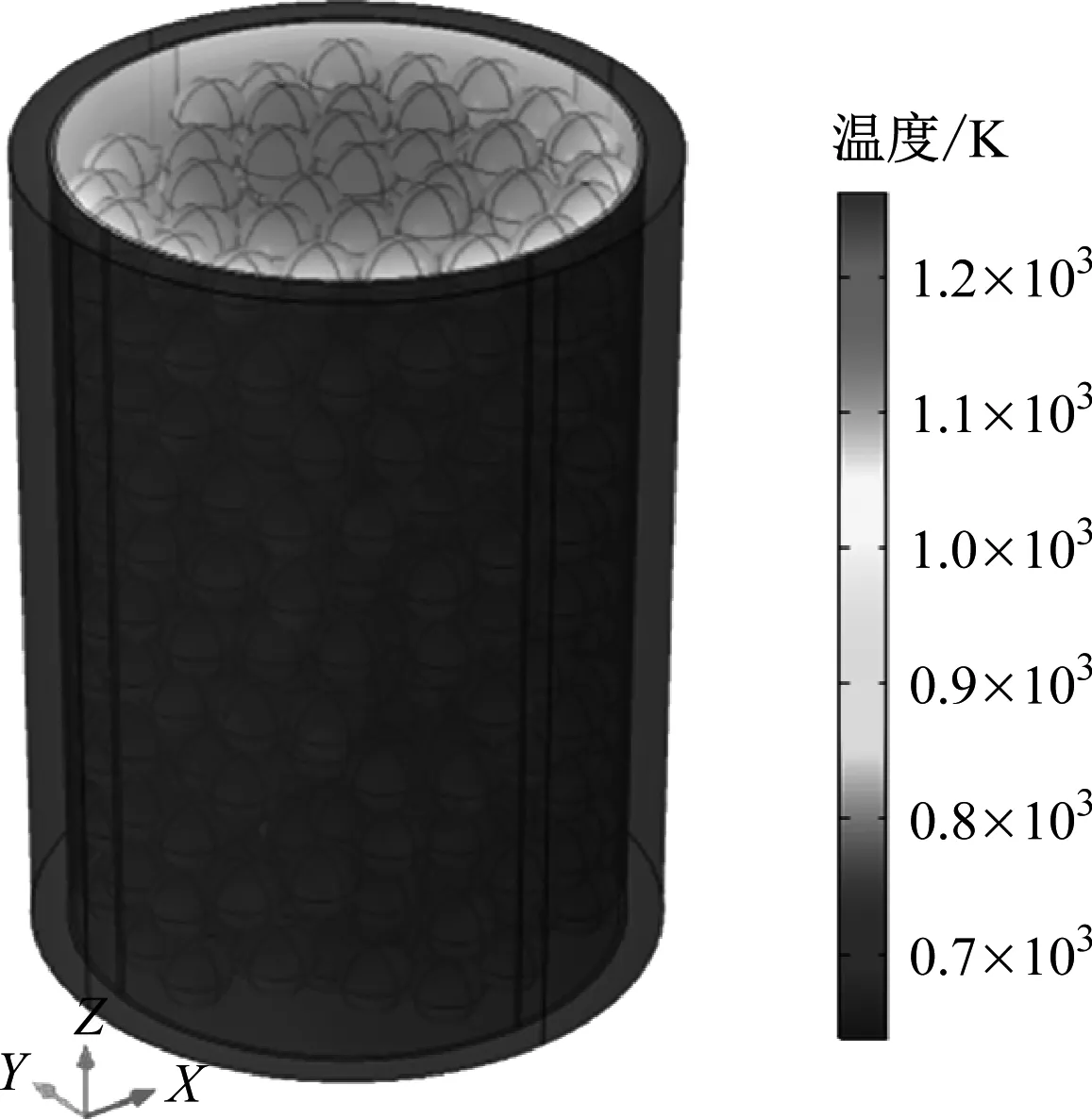
(a) 整体温度分布

(b) 截面温度分布图8 多区域模型数值计算结果Fig.8 Numerical results of multi-region model

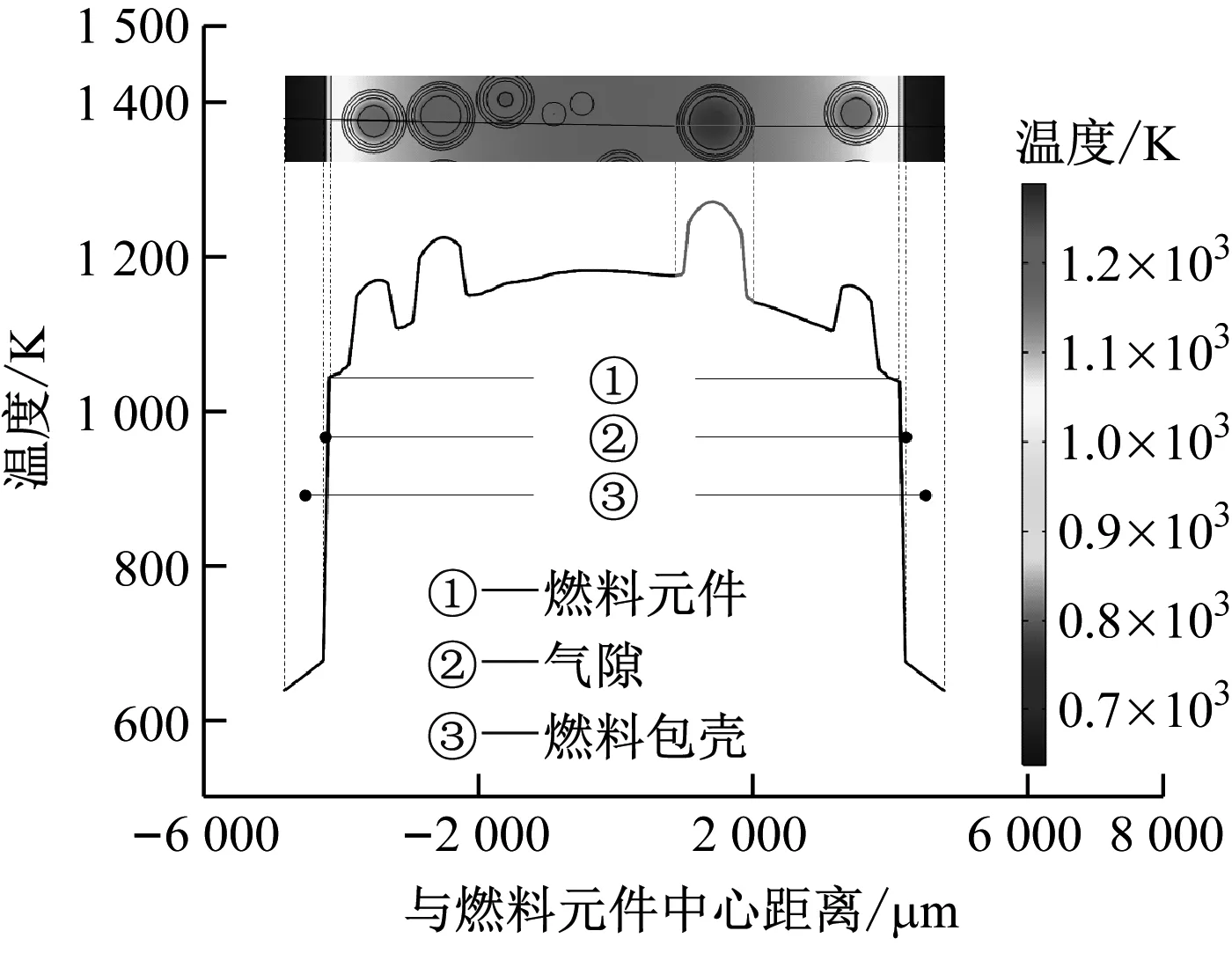
(a) FCM燃料元件

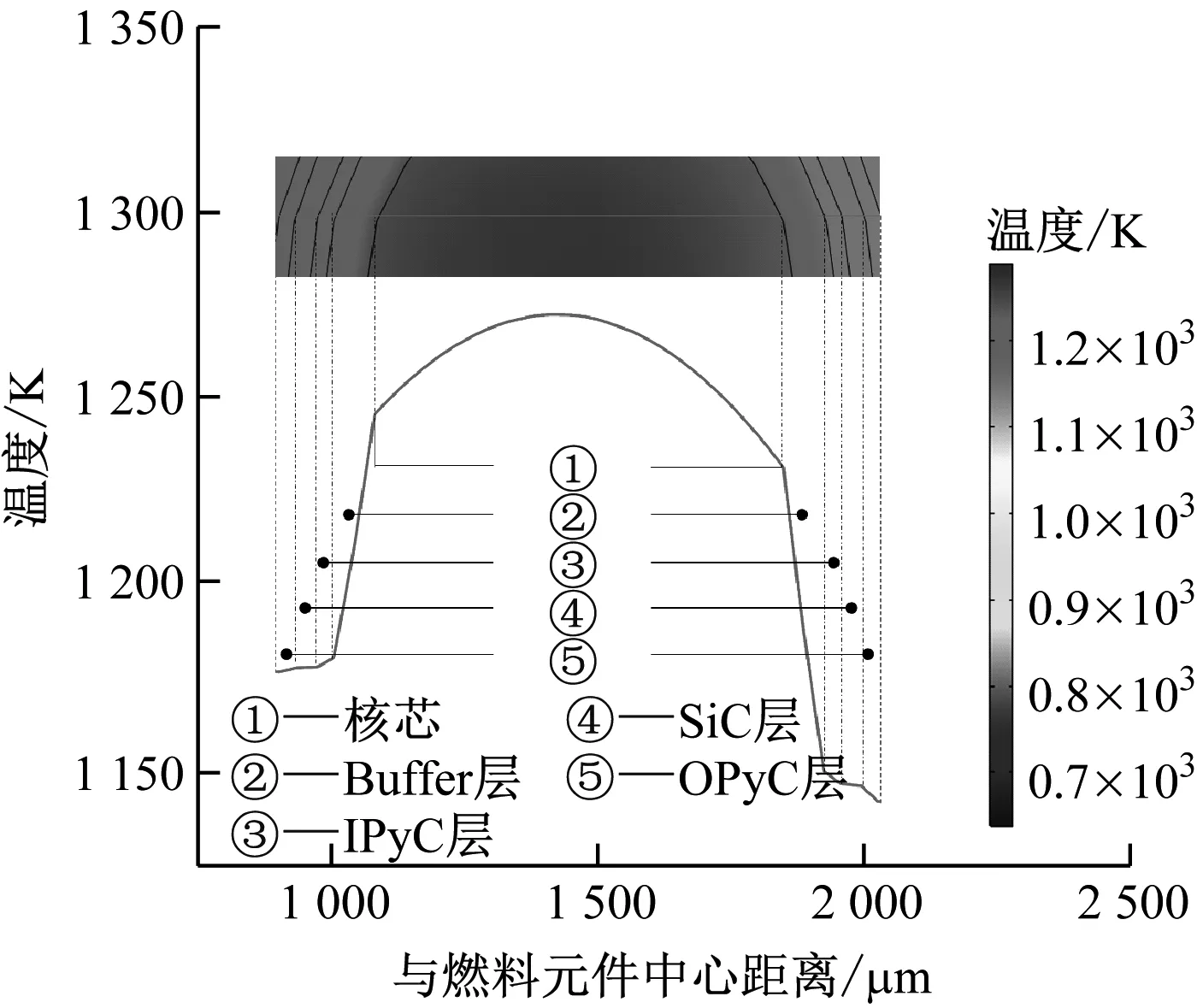
(b) TRISO燃料颗粒图9 沿XZ平面中心线的温度分布Fig.9 Temperature distribution along the central line of XZ plane

2.2 不同填充率下FCM燃料元件的温度分布

取不同颗粒填充率(35%、40%和45%)的FCM燃料元件进行计算并比较其温度分布。FCM燃料芯块在XZ平面中心线的温度分布如图10(a)所示,温度分布中峰值出现在TRISO燃料颗粒位置;随着填充率增加,燃料颗粒中心区域的温度分布总体上有所降低。这是因为在相同线功率下,当颗粒填充率增加时,对应每个TRISO燃料颗粒的功率密度降低。图10(b)比较了不同填充率下FCM燃料芯块的径向平均温度分布,总体上径向平均温度随着填充率的增加而略有升高。图中①、②、③区域的径向平均温度呈有规律的“坡形”分布,由于这些区域中间部分燃料核芯的体积分数更大,因而对应的径向平均温度相对更高。

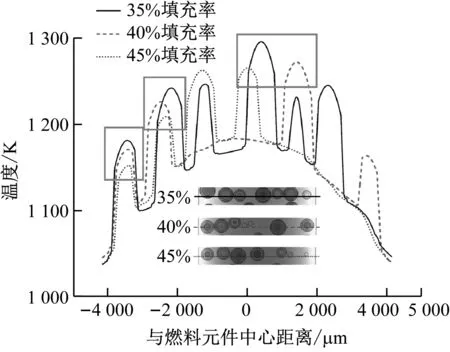
(a) XZ平面中心线温度分布

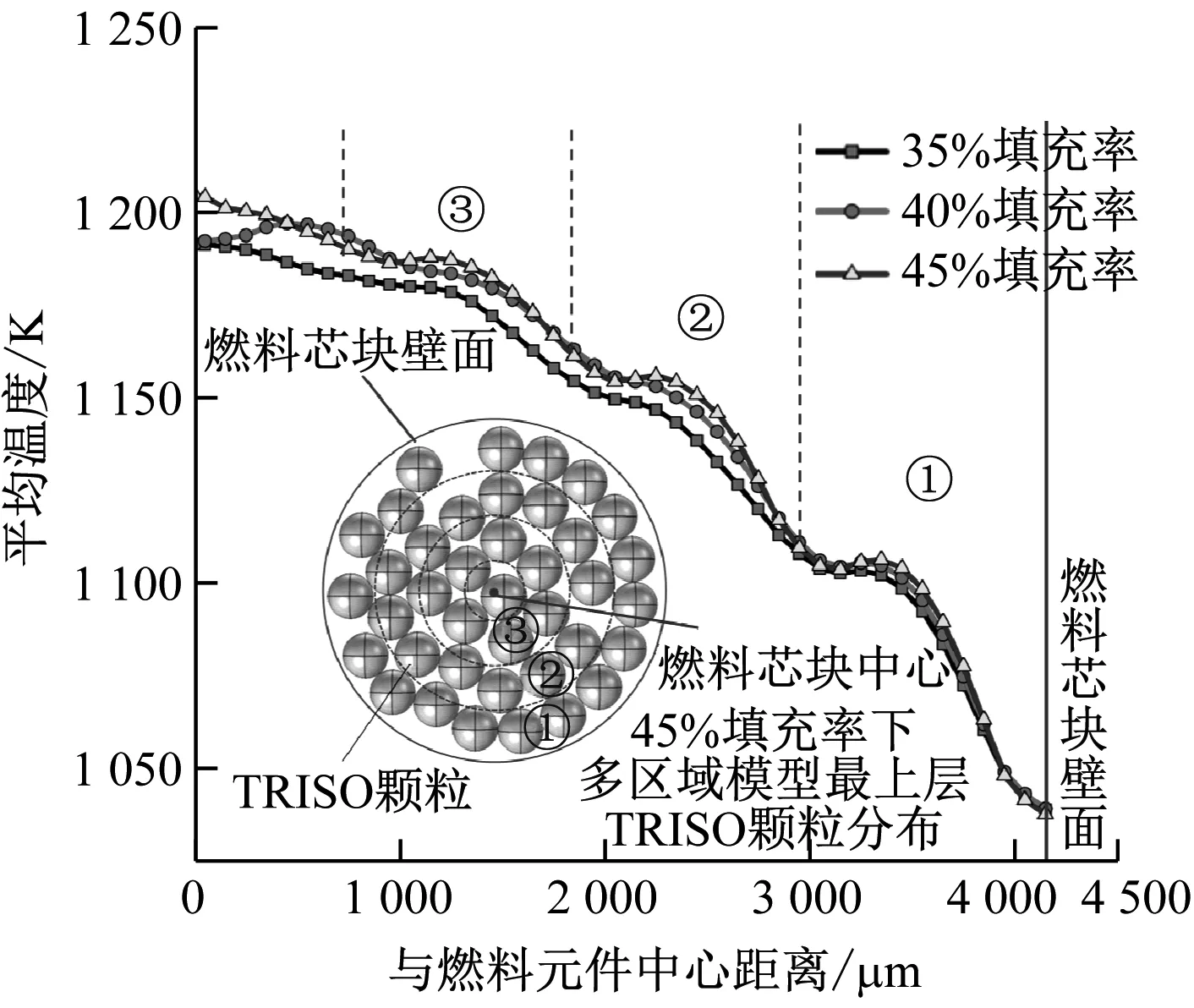
(b) 径向平均温度分布图10 不同填充率下FCM燃料芯块的温度分布

2.3 不同颗粒随机分布下FCM燃料元件的平均温度和最高温度

对不同颗粒填充率的FCM燃料元件分别取60种不同颗粒随机分布的多区域模型进行计算。图11给出了FCM燃料芯块平均温度和最高温度的频率分布直方图。这些直方图总体上呈正态分布,即中间区域频率相对较高,两边区域频率相对较低。统计不同颗粒随机分布下平均温度和最高温度的平均值和极差(最大值与最小值之间的差值),结果如表5所示。由平均值计算结果可以看出,随着填充率的增加,燃料芯块的最高温度会由于TRISO燃料颗粒功率密度的降低而降低。由于燃料颗粒的导热系数比SiC基体的导热系数小,当颗粒填充率增加时,燃料芯块的等效导热系数降低,因此平均温度平均值略有升高。由极差计算结果可以看出,燃料芯块内TRISO颗粒分布的随机性对平均温度的影响较小,当填充率为45%时,平均温度的极差小于1 K。最高温度受到颗粒随机分布的影响较大,当填充率为35%时,最高温度的极差接近17 K。此外,极差会随着填充率的减小而增加,这是由于填充率减小会使得颗粒分布的自由度增加,从而导致平均温度和最高温度分布的离散程度增加。

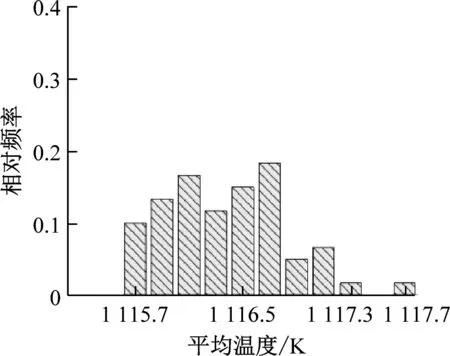
(a) 35%填充率下平均温度分布

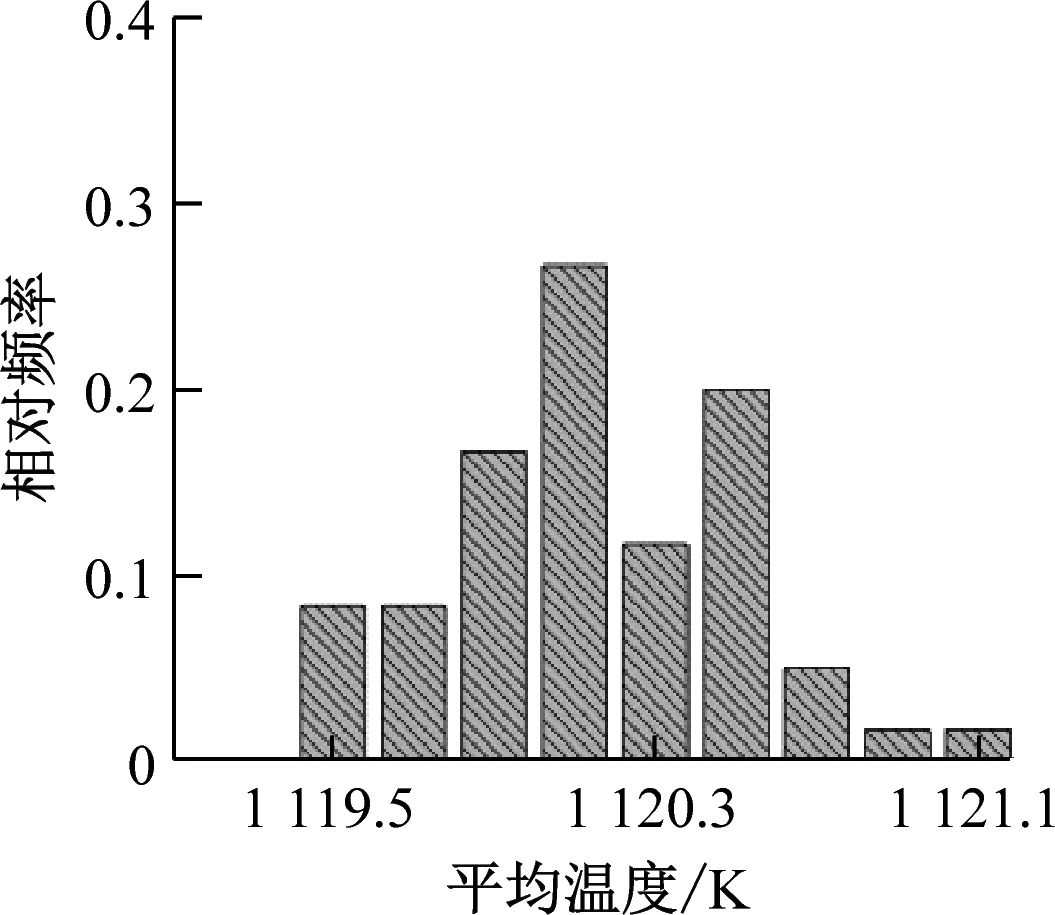
(b) 40%填充率下平均温度分布

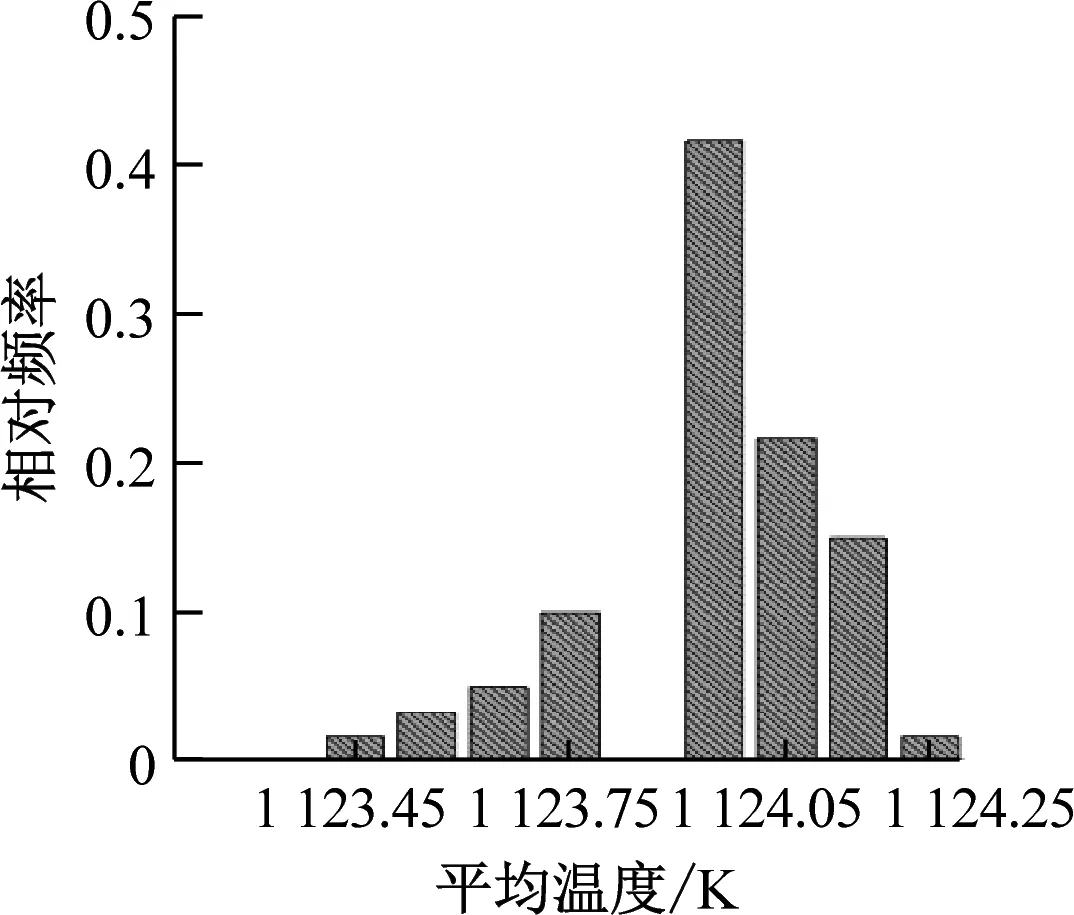
(c) 45%填充率下平均温度分布

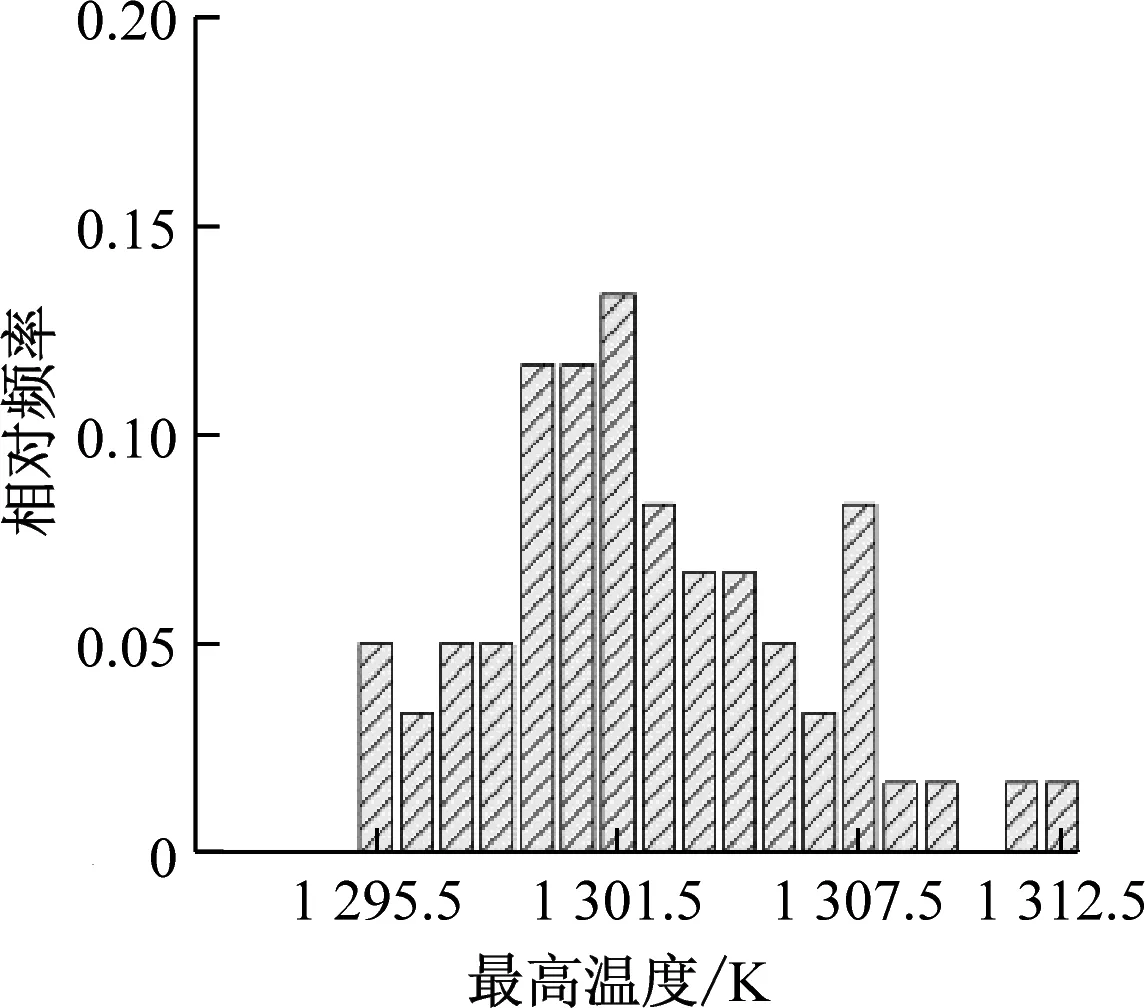
(d) 35%填充率下最高温度分布

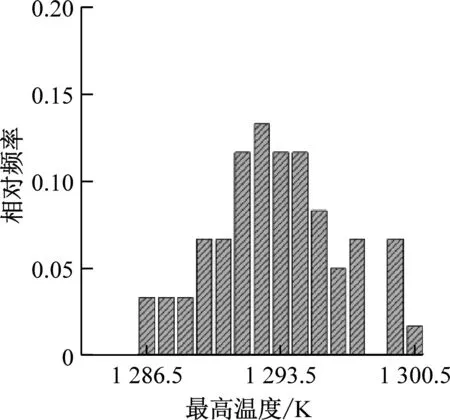
(e) 40%填充率下最高温度分布

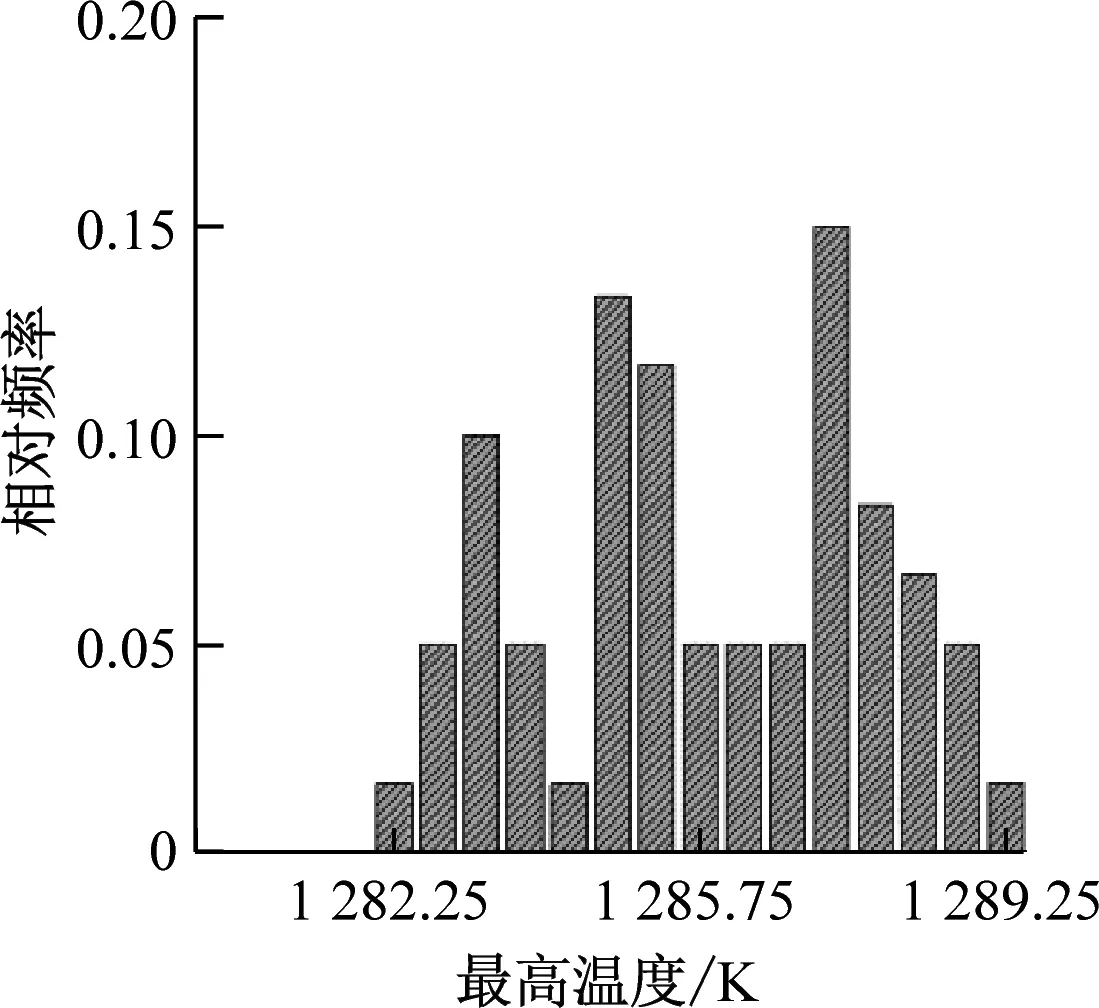
(f) 45%填充率下最高温度分布图11 平均温度和最高温度的频率分布直方图Fig.11 Frequency distribution histogram of the average temperature and the maximum temperature

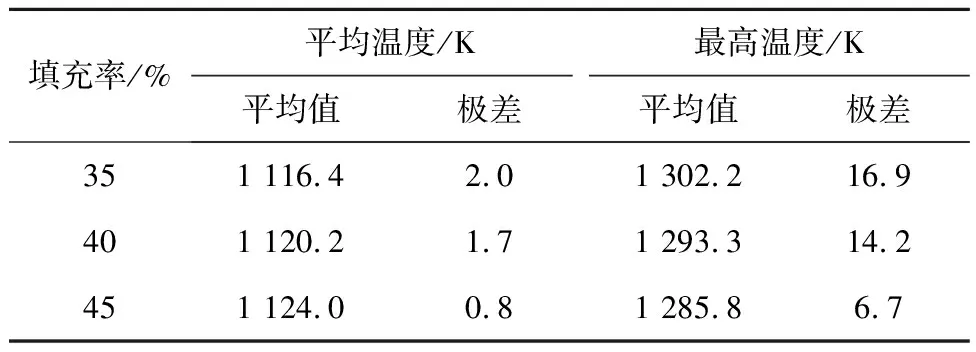
表5 平均温度和最高温度的统计结果

3 结 论

(1) 提出了一种FCM燃料元件内TRISO燃料颗粒随机分布的建模方法。该方法的核心思想是首先对FCM燃料芯块分层并将TRISO燃料颗粒小球平均分放在每一层内,随后采用拟物拟人算法使燃料颗粒小球随机分布在各层内,再调整各燃料颗粒小球的轴向位置,以达到轴向随机分布的效果,最终使TRISO燃料颗粒弥散在FCM燃料芯块内。

(2) FCM燃料元件中心区域温度高,沿径向温度降低。TRISO燃料颗粒特别是燃料核芯的温度明显高于周围基体的温度,温差可达130 K甚至更高;其中最大的温度梯度出现在Buffer层。

(3) 在相同线功率下,随着TRISO颗粒填充率的增加,燃料芯块的最高温度降低,平均温度略有升高。受到颗粒分布随机性的影响,当颗粒填充率减小时,平均温度和最高温度分布的离散程度均增加。但总体而言,颗粒的随机分布对燃料芯块平均温度的影响较小。