用平行线之间的等积变形计算图形的面积

邹 琴

（重庆市科学城明远未来学校）

小朋友，两条平行线之间的距离是处处相等的，例如图1中，直线AD 平行于直线EJ，AE＝BG＝CI＝DJ。

图1

三角形AFH、三角形BFH、三角形CFH、三角形DFH的底都是FH，高分别是AE、BG、CI、DJ。因为三角形的面积＝底×高÷2，所以通过计算可知，三角形AFH 的面积＝三角形BFH 的面积＝三角形CFH 的面积＝三角形DFH的面积，即同底等高的三角形的面积是相等的。

我们在计算图形的面积时，可以应用平行线之间的等积变形，把题目由难变易、由繁变简，这是计算图形面积的一种重要的策略。

例题1图2 中，小正方形的边长是7厘米，大正方形的边长是10厘米。阴影部分的面积是多少？

图2

把三角形ACH 分为三角形ABH 和三角形BCH 两部分。运用直线BE和直线CD的平行关系，把三角形BCH进行等积变形，将C拉动到D（如图3），你会发现三角形BCH与三角形BDH同底（HB为底）等高（CB＝DE），所以面积相等。求三角形ACH的面积可转化为求三角形ABD的面积。三角形ABD的面积＝AB×CD÷2＝7×10÷2＝35（平方厘米），所以阴影部分的面积是35平方厘米。

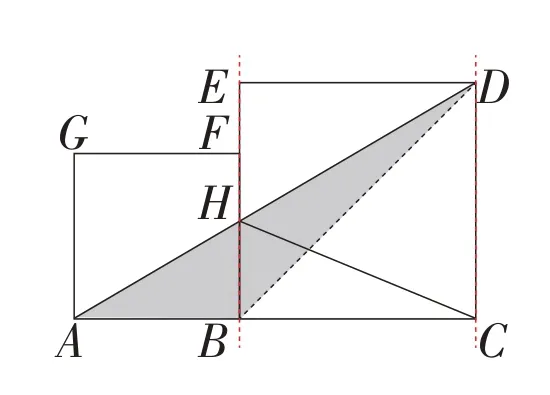
图3

例题2已知长方形AEFD的面积是30 平方厘米（如图4），那么阴影部分的面积是多少？

图4

把三角形ABG 分为三角形AEG和三角形EBG 两部分，运用直线EF 和直线BC 的平行关系，把三角形EBG 进行等积变形，将B 拉动到C（如图5），你会发现三角形EBG与三角形ECG 同底（EG 为底）等高（BE＝CF），所以面积相等。求三角形ABG 的面积可转化为求三角形AEC的面积。

图5

三角形AEC的底就是长方形AEFD的宽，三角形AEC的高BC等于长方形AEFD 的长AD，长方形AEFD 的面积＝AE×AD＝30（平方厘米），三角形AEC 的面积＝AE×BC÷2＝AE×AD÷2＝30÷2＝15（平方厘米），阴影部分的面积是15平方厘米。

例题3正方形BCDE、正方形ABFG 的边长分别是10 厘米、8 厘米（如图6），求图中阴影部分的面积。

图6

观察图6，你会发现线段AF、线段BD 都与线段AC 成45°角，可知直线AF与直线BD互相平行。运用直线AF与直线BD的平行关系，把三角形ADF 进行等积变形，将D 拉动到B（如图7），你会发现三角形ADF 与三角形ABF 同底（AF 为底）等高（DJ＝BI），所以面积相等。求三角形ADF的面积可转化为求三角形ABF 的面积。三角形ABF 的面积＝8×8÷2＝32（平方厘米），所以阴影部分的面积是32平方厘米。

图7

小朋友，运用等积变形，可以巧妙解决面积计算问题，你学会了吗？