基于SPH-FEM方法的土中浅埋爆炸成坑效应研究

崔莹，赵梦婷，李章剑，方军，赵奔

1.西安石油大学土木工程学院，陕西 西安 710065

2.陕西省油气井及储层渗流与岩石力学重点实验室，陕西 西安 710065

3.西安石油大学机械工程学院，陕西 西安 710065

4.西安建筑科技大学土木工程学院，陕西 西安 710055

随着我国基础建设的飞速发展，土中浅埋爆炸在各类工程建设中的应用越来越广泛[1]。在爆炸荷载下，土体的初始天然密度和含水率发生变化，并且土体的各种地质因素对浅埋爆炸中冲量的传递又有较大影响。加之土中浅埋爆炸过程较为复杂，既有土的破损，又涉及爆轰产物和爆炸冲击波的传播[2-7]。因此，建立合理描述土中浅埋爆炸效应的有效方法是学者们关注的一个问题，也使得针对土体在爆炸荷载作用下的动力响应和土体参数研究成为必要[8]。

浅埋爆炸的爆坑形成与土体类别以及炸药类型等因素有关。刘琦等[9]采用ANSYS/AUTODYN进行仿真分析，并对土中爆炸的地面冲击效应进行了研究，结果表明随着装药比例埋深的增加，爆炸应力波的分布也随之改变，中心区迅速增大，地表区迅速减小，近地表逐渐增大。冯伟涛等[10]归纳了国内外炸药近地面爆炸成坑效应研究情况，分析了爆炸形成的爆坑尺寸计算公式和适用条件。穆朝民等[11]研究了在变埋深情况下，炸药在土中爆炸成坑和伴随的应力波传播规律，得到了变埋深条件下应力波在土中传播规律、爆炸成坑半经验公式、半封闭爆炸阶段弹坑半径预估公式。贾永胜等[12]对低含水率砂土和饱和砂土进行了一系列爆炸成坑现场试验，分析了炸药药量、炸药埋深以及土体含水率等因素对爆坑的影响。

从上述研究内容可知，学者们在土中爆炸试验和数值模拟方面进行了许多工作，获取了许多有效的结论。然而利用传统的ALE(arbitrary lagrange-euler)有限元方法模拟土中爆炸，虽然可以很好地模拟出冲击波在土介质中的快速传播，但由于有限元法依赖于网格，很难精准的处理土体爆炸后飞溅，破碎等大变形方面的问题。同时，SPH(smooth particle hydrodynamics)作为一种无网格的数值方法，对于大变形和流体流动等难题，处理得相对精确，但其也有计算时间长、稳定性差以及精准度低等缺点。SPH-FEM耦合法能兼顾两者的优势，在保证精度的同时，提高计算效率[13-14]。本文通过设计开展土中浅埋静爆试验，获取浅埋爆炸爆坑参数，同时基于SPH-FEM方法和ALE方法分别建立了土中浅埋爆炸数值模型，对比数值模拟结果与试验结果，验证SPH-FEM耦合法针对土中爆炸问题数值模拟的有效性。进一步通过对比同时刻SPH-FEM与ALE的模拟结果与试验结果的误差，证实了SPH-FEM方法在模拟土中浅埋爆炸的优越性，最终依据数值模拟结果并通过数学拟合，研究建立了浅埋爆炸条件(比例埋深不大于0.8 m/kg1/3)下炸药埋深与爆坑半径的关系表达式。

1 土中浅埋静爆试验

在试验现场开挖1 200 mm×900 mm×150 mm(长×宽×高)的埋设用坑，剖面图如图1所示。试验所用炸药为柱形TNT，药量为9.35 kg，试验场地开挖区域土质为黏性土，由于炸药比例埋置深度为0.07 m/kg1/3，小于0.8 m/kg1/3，属于浅埋爆炸[15]，现场炸药布置及回填如图2所示。

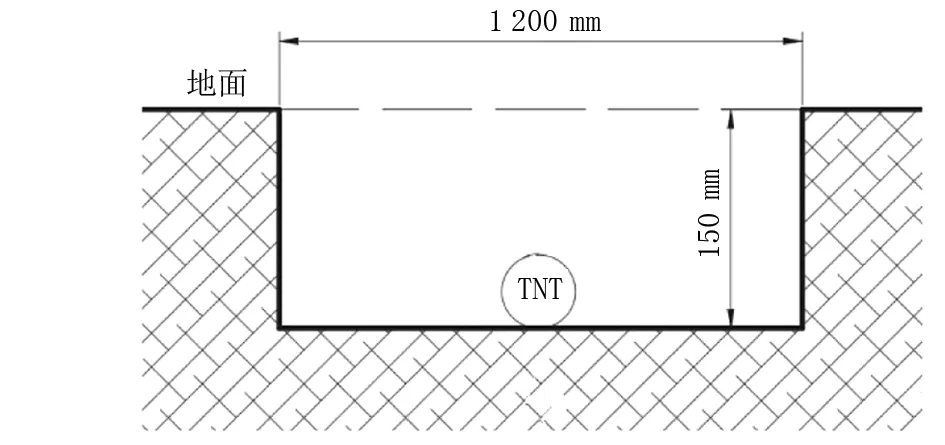
图1 试验场地布置剖面图

图2 炸药布置及回填后场地示意图

爆炸后的土体变形情况如图3所示，由图3可知，土体在吸收了炸药爆炸释放的能量后，产生了较大的变形。由于埋置深度较小，土体的弹性变形吸收的能量达到饱和后，土体迅速隆起，将失效的土颗粒和土块抛掷出去，试验形成爆破漏斗。依据爆炸力学中对于爆破漏斗的描述，主要体现浅埋爆炸能量的参数是爆坑半径r，可见深度H，以及唇缘半径rh，唇缘堆积高度h和最大堆积距离L[16]，如图4所示。现场测量两个主要参数爆坑半径r与可见深度H的测量结果如表1所示。

表1 试验测得爆坑尺寸参数

图3 土体变形图 图4 爆炸漏斗示意图

2 浅埋爆炸荷载下基于SPH-FEM方法的土体损伤及破坏数值模拟

2.1 模型建立

通过对试验参数进行分析，考虑对称性，采用ANSYS ADPL建立1/2模型，定义单元属性和材料类型并进行网格划分。利用LS-Prepost将炸药和爆炸近区的土转化为SPH粒子，并修改关键字。ANSYS ADPL定义NODES组，添加接触和边界条件，通过设置合适的SPH粒子密度和FEM网格确保计算结果的准确性，提高计算效率，所建立的有限元模型如图5所示。

图5 有限元模型 图6 边界和接触定义

基于实际的约束条件，土体单元两边及底部选择透射边界，顶部选择自由边界。FEM单元和SPH粒子之间选择固连接触，利用*CONTACT_TIED_TO_SURFACE_OFFSET建立接触对，对称面分别设置SPH对称边界和FEM对称边界，并利用*DEFINE_BOX控制粒子范围，边界和接触定义见图6，单位制取为mm-ms-MPa。

2.2 材料本构模型

1)土体材料。土的本构模型有多种，本文使用*MAT_SOIL_AND_FOAM材料模型对浅埋爆炸荷载下土体的动态力学响应进行数值模拟，土体材料具体参数如表2所示。其中，RO为质量密度，g/mm3；G为剪切模量，MPa；BULK为VCR=0时使用的卸载体积模量，MPa；A0，A1，A2为塑性屈服函数常数；PC为拉伸断裂的压力极限，MPa；VCR为体积破碎选项；REF为参考几何形状初始化压力，MPa。

表2 土体参数

2)炸药材料。为了真实地模拟TNT爆炸，本文采用*MAT_HIGH_EXPLOSIVE_BURN高能炸药燃烧模型并用JWL状态方程进行计算。JWL状态方程可表示为：

(1)

式中：P为爆炸压力，MPa；V为爆炸物的相对体积；E为爆炸物单位体积初始内能，J；w、A、B、R1、R2为材料常数。

炸药材料参数如表3所示。其中，D为引爆速度，mm/ms；PCJ为Chapman-Jouget压力，MPa；BETA为燃烧标志；K为体积模量，MPa；SIGY为屈服应力，MPa。

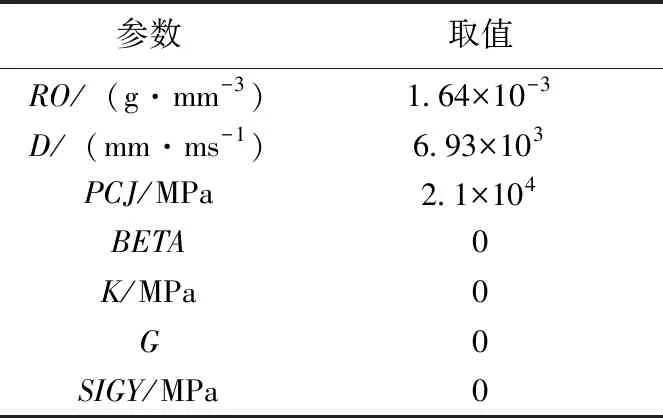
表3 炸药材料参数

2.3 SPH-FEM结果与试验结果比较

为了验证SPH-FEM方法的有效性，将试验得到的爆坑半径r和可见深度H与模拟结果进行校核，如图7所示。两个主要参数爆坑半径r与可见深度H的的数值模拟结果与试验结果的比较如表4所示。由表4可知，爆坑半径r的相对误差在12.4%，可见深度H的相对误差在6.36%，均未超过±15%，测量的尺寸偏差10%左右。与试验结果的比较分析表明，采用SPH-FEM方法进行土中浅埋爆炸数值模拟，所获得的结果是合理且可以接受的。

表4 数值模拟与试验结果对比

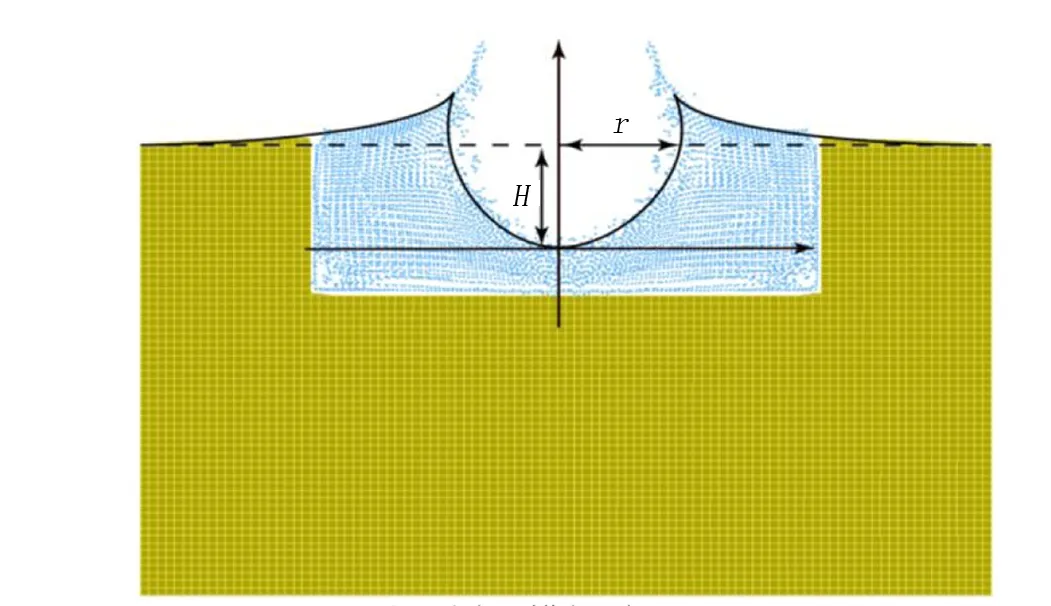
图7 爆坑模拟结果

2.4 土中爆炸冲击波传播规律分析

为进一步验证SPH-FEM方法的有效性，如图8所示选取沿深度及距离爆心位置比例距离为0.17、0.21、0.31 m/kg1/3的三个测点，提取土中爆炸冲击波压力时程曲线如图9所示。由图9可知，随着时间的增加，各个测点的爆炸冲击波峰值压力急速衰减，最后趋近于零，不同测点的爆炸冲击波压力也有所差异，随着深度和距离的增加，爆炸冲击波的峰值压强急剧衰减，与客观规律相一致。综合以上分析表明，SPH-FEM方法可以有效模拟浅埋爆炸荷载下的土体成坑效应。

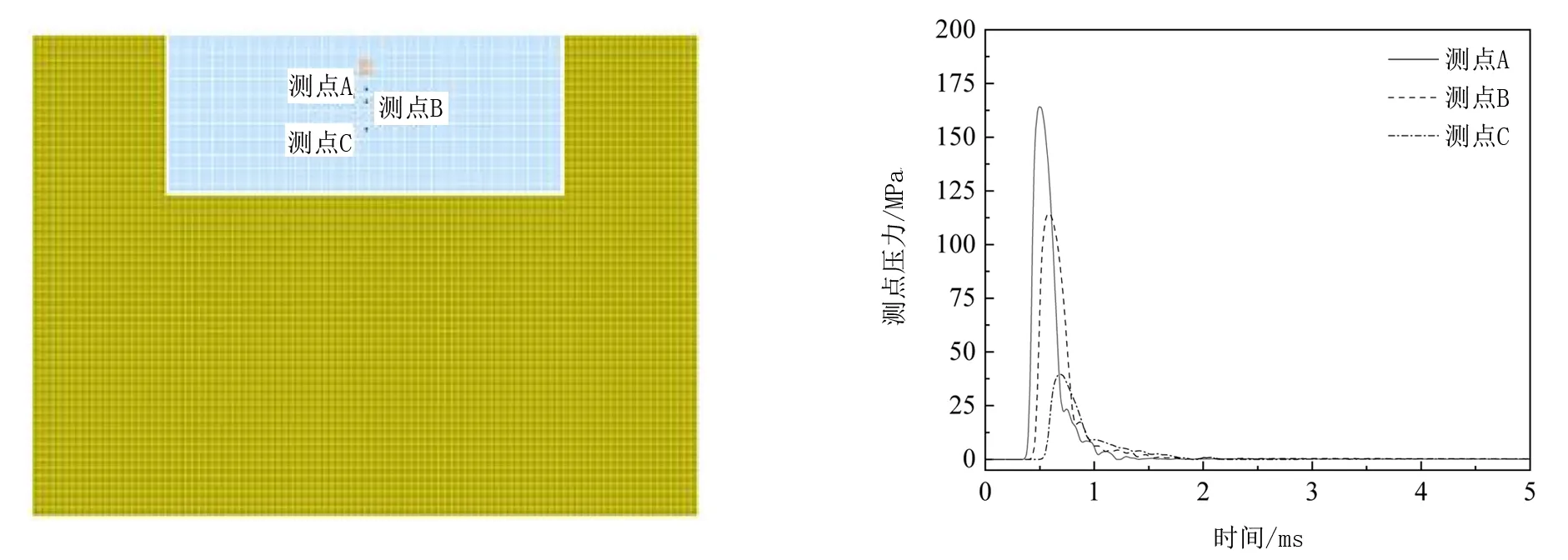
图8 测点布置图 图9 不同测点压力时程曲线

3 SPH-FEM方法与ALE方法数值模拟结果比较

分别采用SPH-FEM方法和ALE方法对土中浅埋静爆试验进行模拟，获取两种方法在不同时刻模拟的爆坑形成过程如图10所示。由图10可知，尽管SPH-FEM方法与ALE方法都可以模拟爆坑的形成过程，但是相同时刻基于SPH-FEM方法模拟获取的土体的变形量要略大于ALE方法，同时SPH-FEM方法模拟的土体抛掷高度与ALE方法有较大差异，这里分析原因主要可能与空气的影响以及SPH粒子的质量有关。由于SPH是一种拉格朗日粒子方法，其中物理量的计算基于单元搜索域中粒子的总和，而爆炸后部分SPH粒子退出了工作，且SPH-FEM方法中边界条件的实现与传统基于网格的方法中边界条件的合并方式完全不同。虽然两种算法都可以对炸药爆炸后土体的运动与抛掷现象进行描述，但是SPH-FEM方法可以清晰地表现出上部土体的剥离现象，而ALE方法表现的相对模糊，且SPH-FEM方法将局部大变形区域进行SPH粒子化避免了网格缠绕和扭曲等问题，将小变形区域网格化，减少了计算上的压力。所以SPH-FEM方法在模拟土中浅埋爆炸方面要较ALE方法更有优势。

图10 爆坑形成过程

4 土中浅埋爆炸炸药埋深与爆坑半径关系建立

土中浅埋爆炸的成坑效应主要受炸药埋深和炸药量的影响，同时炸药埋深和炸药量也是确定爆坑大小和形状的重要参数[17]。通过SPH-FEM方法，进一步提取得到了9.35 kg TNT炸药在不同深度产生弹坑的半径数据如图11所示。由图11可知，土中浅埋爆炸爆坑半径与炸药埋深之间呈现出前期爆坑半径随埋深的增加而增加，到达峰值后爆坑半径又随着埋深的增加而减少的趋势。为了能够有效判断在确定炸药量的前提下，爆坑半径与炸药埋深的对应关系，通过数学拟合的方法对9.35 kg TNT炸药在不同深度产生的弹坑的半径数据进行了曲线拟合，并建立了相应的经验曲线式(2)。利用建立的经验曲线式(2)对数据进行拟合得到了炸药埋深d与爆坑半径r的关系曲线，如图11所示。所建立的经验曲线式(2)可以有效判断9.35 kg TNT炸药时炸药埋深与爆坑半径的关系。

图11 炸药埋深与爆坑半径的关系

(2)

式中：d为炸药埋深，mm。

5 结论

1)土中浅埋爆炸在形成爆破漏斗的同时会有颗粒飞溅效应，SPH-FEM方法可以有效模拟出土中浅埋爆炸过程中的土体变形及抛散效果，与实际误差较小；

2)SPH-FEM方法和ALE方法都可以有效模拟土中浅埋爆炸爆炸冲击波的球形波阵面，而SPH-FEM方法较ALE方法可更有效地模拟冲击波形成的超压造成周围土体急剧变形直至破碎的过程；

3)SPH-FEM方法和ALE方法都可以有效模拟土体爆炸成坑过程，且与试验现象基本符合，SPH-FEM方法可以更加细致地表现出土体受到爆炸荷载后的剥离现象，计算效率更高；

4)结合试验数据和数值模拟获取的炸药埋深和爆坑半径的离散数据，可以基于数学拟合建立炸药埋深与爆坑半径表达经验公式。本文所建立的经验公式可以有效判断在9.35 kg TNT炸药量时，浅埋爆炸过程中土的爆坑半径与炸药埋深的关系。