2023年高考全国乙卷物理压轴题探析

黄尚鹏

(湖北省监利市实验高级中学)

2023年高考全国乙卷物理压轴题严格依据高中物理课程标准,依托高考评价体系,深化基础性和综合性,聚焦学科核心素养,加强关键能力考查,在竖直下落小球和薄圆盘弹性碰撞多过程问题中,综合考查匀变速运动、追及问题、弹性碰撞、动量守恒定律、机械能守恒定律等力学主干知识,深入考查了学生理性分析问题的思维过程,考查学科综合应用能力、数学运算能力、创新能力,有较好的区分度,体现选拔功能,下面我们对此题进行全面深入的分析和探讨.

1 知识准备:一般弹性碰撞的公式及推论

如图1所示,光滑水平面上有两个质量分别为m1和m2的小球发生弹性碰撞,碰撞前m1和m2的速度分别为v1、v2,求碰撞后m1和m2的速度.

图1

分析此问题为弹性碰撞“动碰动”模型,计算碰后速度是难点,若采用降幂法求解计算量非常大,可先采用变换参考系法转换成“动碰静”模型,再用结论法直接表示碰后速度,最后再变回地面参考系即可表示碰后速度,具体操作方法如下.

如图2所示,选以速度v2做匀速运动的物体为参考系(为惯性系,动量守恒定律和机械能守恒定律仍然成立),碰撞前m1的速度为v1－v2,m2静止,故碰后m1、m2的速度分别为

图2

因此在地面参考系中,由绝对速度＝相对速度＋牵连速度,得到碰后m1、m2的速度分别为

推论1)若m1＝m2,则,即碰撞后两球速度发生交换.

2)v1－v2＝,v1－v2为碰前m1靠近m2的相对速度,称为相对接近速度,为碰后m2远离m1的相对速度,称为相对分离速度,即相对接近速度等于相对分离速度.

2 对原题的分析与解答

原题(2023年全国乙卷25题)如图3所示,一竖直固定的长直圆管内有一质量为M的静止薄圆盘,圆盘与管的上端口距离为l,圆管长度为20l.一质量为的小球从管的上端口由静止下落,并撞在圆盘中心,圆盘向下滑动,所受滑动摩擦力与其所受重力大小相等.小球在管内运动时与管壁不接触,圆盘始终水平,小球与圆盘发生的碰撞均为弹性碰撞且碰撞时间极短.不计空气阻力,重力加速度大小为g.求:

(1)第一次碰撞后瞬间小球和圆盘的速度大小;

(2)在第一次碰撞到第二次碰撞之间,小球和圆盘间的最远距离;

(3)圆盘在管内运动过程中,小球与圆盘碰撞的次数.

(1)设小球从管的上端口由静止下落距离l时获得的速度为v0,由动能定理得解得.

小球以速度v0与静止的圆盘第一次发生弹性碰撞,碰撞后小球和圆盘的速度分别为,根据动量守恒定律(选向下为正方向)和机械能守恒定律,得,得

(2)第一次碰撞后,小球做竖直上抛运动,圆盘所受滑动摩擦力与重力平衡,匀速下滑,所以只要圆盘下滑速度比小球快,二者间距就不断增大,当二者速度相等时,间距最大,设经过时间t二者速度相等,则有,解得.此段时间内小球和圆盘的位移分别为,故小球和圆盘间的最远距离为

或者画出碰撞后的v-t图像如图4所示,当二者速度相等时,间距最大,最大间距为图中阴影部分的面积,即.

图4

还可以圆盘为参考系,小球相对圆盘以向上的初速度v0做竖直上抛运动,最大间距为竖直上抛运动上升的最大高度.

(3)为了表述方便,我们约定第n次(n≥1)碰撞前瞬间小球和圆盘的速度分别为vmn、vMn,碰撞后瞬间小球和圆盘的速度分别为,则

方法1(数学归纳法)我们先分析前面几次碰撞和运动过程,再归纳总结出一般规律.

小球与圆盘第二次发生弹性碰撞,根据动量守恒定律和机械能守恒定律,得

小球与圆盘第三次发生弹性碰撞,根据动量守恒定律和机械能守恒定律(方程略),得

小球与圆盘第四次发生弹性碰撞,根据动量守恒定律和机械能守恒定律(方程略),得

归纳总结:每次碰撞后到下一次碰撞前,经历的时间都相等,即,每次碰撞后瞬间圆盘的速度依次为

即每次碰撞后瞬间圆盘的速度都比上一次碰撞后瞬间圆盘的速度增加,恰好构成等差数列,因此第一次碰撞后到第二次碰撞前,圆盘以速度匀速下降的距离

即圆盘每次碰撞后到下一次碰撞前下降的距离依次为2l,4l,6l,…,恰好构成以d＝2l为公差的等差数列,到第四次碰撞时,圆盘已下降的距离为2l＋4l＋6l＝12l,此时圆盘距离管下端口长度为20ll－12l＝7l,第四次碰撞后,若发生下一次碰撞,圆盘将向下移动8l＞7l,说明第四次碰撞后,圆盘将落出管口外,因此圆盘在管内运动过程中,小球与圆盘碰撞的次数为4次.

方法2(相对运动法)我们以圆盘为参考系来描述小球的运动情况.

如图5所示,第一次碰撞前小球相对圆盘的接近速度大小为v0,根据弹性碰撞的推论:相对接近速度等于相对分离速度,碰撞后小球相对圆盘的分离速度大小仍为v0,则第一次碰撞后到第二次碰撞前,小球相对圆盘做竖直上抛运动,当再次返回抛出点时,小球相对圆盘的接近速度大小仍为v0,此过程经历的时间为.由于第二次碰撞前小球相对圆盘的接近速度大小仍为v0,以后小球相对圆盘的运动周期性重复,即每次碰撞前小球相对圆盘的接近速度大小和碰撞后小球相对圆盘的分离速度大小都为v0,每次碰撞后到下一次碰撞前,经历的时间都为,且对于第n次(n≥1)碰撞,由一般弹性碰撞公式,可知

图5

方法3(质心法)以小球和圆盘构成的系统的质心为研究对象来描述质心的运动情况.

小球和圆盘构成的系统的合外力始终为mg,根据质心运动定理,质心C的加速度,即质心的加速度恒定.

以小球从管的上端口由静止下落开始计时,t＝0时刻,质心的初速度为零,故质心做初速度为零的匀加速运动.由于小球和圆盘的质量之比为1∶3,故系统的质心到小球和圆盘的距离之比为3∶1,即t＝0时刻,质心到小球和圆盘的距离分别为0.75l和0.25l,质心距离管下端口长度为19.25l,如图6所示.

图6

第一次碰撞前小球做自由落体运动的时间为

由方法2可知,每次碰撞后到下一次碰撞前,经历的时间都为

故第n次碰撞时(此时小球、圆盘以及系统的质心三者重合)经历的总时间为

质心C运动的位移为.因此,当n＝1时,yC1＝0.25l;当n＝2时,yC2＝2.25l;当n＝3时,yC3＝6.25l;当n＝4时,yC4＝12.25l;当n＝5时,yC5＝20.25l＞19.25l,圆盘已落出管口外,因此圆盘在管内运动过程中,小球与圆盘碰撞的次数为4次.

方法4(递推法)我们直接分析第n次碰撞和运动过程,建立递推关系式求通项.

小球与圆盘第n次发生弹性碰撞,根据动量守恒定律和机械能守恒定律得

解得

在管道中第n次碰撞后到第(n＋1)次碰撞前,设经过时间tn二者位移相等,则有,解得

此时小球的速度

圆盘的速度

显然,

因此,每次碰撞后到下一次碰撞前,经历的时间都相等,即

3 试题赏析

本题既源于教材又不拘泥于教材,粗看感觉很眼熟,让学生有信心去完成答题,但细看后发现对能力的要求较高,体现了命题低起点高要求的特点.本题以学习探索情境为载体,除考查一般的理解能力、分析综合能力外,还突出考查了模型建构能力、推理论证能力、用数学方法解决物理问题的能力和创新能力等关键能力,有较好的区分度,体现了选拔功能.

1)本题第(1)问考查弹性碰撞“动碰静”模型,第(2)问考查“竖直上抛运动”模型和追及模型,强化必备知识考查,深化基础性,引导教学回归课标、教材.

2)本题第(3)问考查了弹性碰撞“动碰动”模型,并且为多次碰撞,一般考生都能根据动量守恒定律和机械能守恒定律列出方程组,但很难计算出正确结果,以致无法归纳总结出一般规律,这就要求学生最好记住一般弹性碰撞的公式及推论,或者先采用变换参考系法将弹性碰撞“动碰动”模型转换成“动碰静”模型,“动碰静”模型可用结论法直接表示碰后速度,最后再变回地面参考系即可快速表示碰后速度,大大降低计算量.为使学生掌握利用一般弹性碰撞公式快速解题的方法和技巧,这里不妨再举一个典型例子.

例题如图7 所示,光滑水平面上有两个质量分别为m1和m2的小球A和B,它们在一条与右侧竖直墙面垂直的直线上前后放置.开始时B球静止,A球以速度v向B球运动.不计各种摩擦,所有碰撞都是完全弹性碰撞.如果要求两球只发生两次碰撞,试确定的范围.

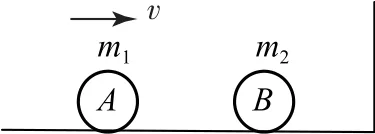
图7

分析选向右为正方向,第一次碰撞后A、B的速度分别为.

①当m1＞m2时,A、B均向右运动,B碰墙后弹回与A发生第二次碰撞,碰后A、B的速度分别为

将v1、v2的表达式代入后,可得

当m1＞m2时,,B向右运动,要使不发生第三次碰撞,首先要求,其次要求B球碰墙返回后追不上A,即要求,因此有

②当m1＝m2时,第一次碰撞后A静止,B向右运动,B碰墙后弹回与A发生第二次碰撞,碰后B静止,A向左运动,只发生两次碰撞,故可取.

③当m1＜m2时,则第一次碰后,v1＜0,A向左运动,B向右运动,B碰墙后返回.若能追上A,则要求－v1＜v2,即,解得故.

将以上3种情况综合起来,便得到可使A、B能且仅能发生两次碰撞的的取值范围为

3)本题第(3)问考查了数学归纳法在物理问题中的应用,归纳法是一种研究问题的基本方法,它是从认识个别的、特殊的事物推出一般原理和普遍事物,对考生的思辨性思维要求较高,考查学生的高阶思维能力,突出关键能力考查,引导减少死记硬背和机械刷题现象,有较好的区分度,体现选拔功能,并且此问还能够运用相对运动法和质心法巧解,从而可快速总结出一般规律,体现了物理思想方法的灵活运用,引导学生多角度思考,培养学生的创新能力.

4)在本题的解答中,方法1即数学归纳法只分析了前面几次碰撞和运动过程,再归纳总结出一般规律,为不完全归纳法,在物理解题中经常采用.而方法4即递推法,直接分析第n次碰撞和运动过程,建立递推关系式,然后由递推公式求通项公式,为完全归纳法.显然递推法比数学归纳法更为严谨,且计算过程更简洁,但对考生的数学能力要求更高.所谓递推法,即当问题中涉及的物理过程较多,且各物理过程具有相同的特点和遵循相同的规律时,可选取有代表性的任一物理过程分析,得出联系相邻物理过程的相关物理量的递推关系式,再根据递推公式求解相关物理量的通项公式,从而达到解决问题的目的的一种科学思维方法.由数列的递推公式求通项公式的问题一般比较复杂,不过只要我们抓住递推数列的递推关系,分析结构特征,善于合理变形,就能找到解决问题的有效途径,使学生深入理解递推法,掌握递推法的应用技巧.

4 教学启示

高考物理命题要落实立德树人的根本任务,坚持正确的育人方向,促进学生德智体美劳全面发展;坚持守正创新,依托高考评价体系,深化基础性,突出对关键能力的考查.在课程改革进入新时期之际,物理学科考试内容改革将在一定程度上推动物理教学变革、高考改革乃至课程改革的发展,同时,也为物理教学提供了一些启示.

1)强调物理必备知识.高中物理课程在结构上注重为全体学生打好共同基础,重视对基本概念、基本规律的理解和掌握.物理知识体系的建构是学生解决物理问题的基础,教科书是教师教学和学生学习的主要资源.因此,要重视教科书内容的选择与编排,注重对教材例题和习题的研究,发掘教材的指导价值.另外,教学中我们不能将知识静态化与孤立化,应注重知识间的联系和知识的迁移.

2)注重培养理解、推理论证、模型建构、实验探究和创新等关键能力.要结合物理学科核心素养进行教学,要通过好的情境素材把核心素养和课程内容进行深度关联.教学中要注重引导学生经历物理概念的建构过程和物理规律的形成过程,体会建构物理模型的思维方式,认识物理模型在探索自然规律中的作用,培养学生建构模型的意识和能力.就习题教学而言,要通过增强习题的开放性和探究性,鼓励学生讨论与多角度作答,促进对学生推理论证、质疑创新等关键能力的培养.要特别重视实验探究,凸显物理实验在发展学生核心素养方面的重要地位和作用,要开足开好实验课,鼓励学生开展各种科学探究活动,提高学生的实验探究能力.

3)加强理论联系实际,发展学生的问题解决能力.教学中要创设联系生产生活实际、科学技术进步的真实情境,把物理知识跟实践情境进行关联,引导学生用物理学的视角观察周围世界、建立物理模型,培养学生灵活运用所学物理知识解决实际问题的能力.要加强习题情境化设计,重视情境化习题教学.情境化试题在高考物理命题中的比例将逐渐加大,代表高考物理命题改革的方向,引领物理教育本原的回归.

总之,一道高考题的设计是经过命题专家深思熟虑的,经典模型不按套路出牌,常考常新将是新高考试题的亮点.教学中要对教材中的典型例题和课后习题多进行“一题多解、一题多变、多题归一”的训练,通过自主独立思考和小组合作探究,挖掘学生潜力,激发学生思维的火花,引导学生在讨论分享中形成多样化的问题解决意识.这样学生才能在新的命题情境和设问方式中明确思维去向,快速找到解决问题的突破口.

(完)