基于WFRFT 频谱预编码的GFDM 系统性能优化方法

王震铎，王朝晖，张若愚

（1.哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001；2.南京理工大学近程射频感知芯片与微系统教育部重点实验室，江苏 南京 210094）

0 引言

随着科学技术的不断发展，通信的意义和内涵不断演变。太赫兹通信、通信感知一体化和智能超表面[1-2]等通信技术也迎来了蓬勃发展。智能制造、智慧医疗、智能家居、智慧城市等新兴业务场景的不断涌现，推动了通信、人工智能、大数据、图像处理和遥感等技术的深度融合[3-4]。从1G 的语音通信到如今5G 的万物互联，通信场景正在向多元化的方向发展[5]。国际电信联盟明确了5G 通信的三大应用场景[6-9]，包括增强型移动宽带（eMBB,enhanced mobile broadband）、大连接物联网（mMTC,massive machine-type communication）以及低时延高超可靠通信（URLLC,ultra-reliable &low-latency communication）。然而当今广泛使用的正交频分复用（OFDM,orthogonal frequency division multiplexing）技术难以满足上述应用场景对通信波形更加严格的要求，作为5G 候选波形的广义频分复用（GFDM,generalized frequency division multiplexing）由于具有更加灵活、高效的优点，成为当前研究的热点。

GFDM 是一种基于时频资源块的非正交多载波调制方案，每个时频资源单位由若干个子符号和子载波构成[10]。GFDM 系统具有良好的时频聚焦特性，能够在多径环境下提供较好的抗干扰性能和频谱利用率[11]，是一种适于物联网、无线电视、卫星通信等领域的调制方式。由于时频资源配置的灵活性，GFDM 可以很容易地实现与正交频分复用（OFDM）的兼容，并且支持多个用户共享物理层资源。从某种意义上说，GFDM 可以视作一种编码OFDM 技术。另外，在GFDM 中，多个子符号共用一个循环前缀（CP,cyclic prefix），节省了频带资源，提升了GFDM 系统的频带利用率。此外，文献[12]表明正交时频空（OTFS,orthogonal time frequency space）可以作为具有简单排列的GFDM 信号进行处理。通过正确选择设计GFDM 参数，可以合成OFDM 和OTFS 等波形。因此以GFDM 系统为研究对象对其他波形技术有一定的参考价值。

为了提高GFDM 系统的性能，减少对相邻信道的干扰以及推进GFDM 技术与物联网、车联网的融合，研究人员一直在深入探究抑制GFDM 系统带外（OOB,out of band）功率泄漏和降低GFDM 系统的峰均功率比（PAPR,peak to average power ratio）等相关问题。针对OOB 问题，文献[13]通过对传统的基于向量的GFDM 系统表征深入研究，提出了一种基于矩阵化表征的GFDM 发射机模型，指出了GFDM 系统OOB 性能与原型滤波器的联系，并为设计最优滤波器提供了参考。文献[14]通过将GFDM 发射信号的功率谱密度表示为GFDM 滤波器系数的函数，将最小化OOB 问题转化为滤波器设计问题，权衡了误码率（BER,bit error rate）性能和OOB 性能。文献[15]利用二次规划方法对原型滤波器加以设计优化以有效抑制GFDM 系统的带外功率。除此之外，文献[16-18]通过GFDM 与索引调制相结合，利用不同子载波的激活状态从而达到降低带外辐射、提高功率放大器效率和频谱效率的效果。针对PAPR 问题，文献[19]通过对GFDM 系统PAPR 性能的理论性能的分析，阐明了滤波器优化PAPR 性能所能达到的限制。文献[20]设计了一种基于梯度下降法的线性预编码器，通过最小化GFDM 信号瞬时功率的方差、二阶矩和三阶矩等统计参数来降低PAPR，并给出了相应的优化算法。文献[21]提出了一种预编码器，通过最小化瞬时功率（IP,instantaneous power），从而降低PAPR。文献[22]提出了一种基于小波变换的技术，可以有效提升系统PAPR 性能。文献[23]结合选择映射（SLM,selective mapping）和部分传输序列（PTS,partial transmit sequence）等技术提出了混合沃尔什-哈达玛预编码技术，以进一步降低发射端的PAPR。文献[24-25]通过加权分数傅里叶变换（WFRFT,weighted fractional Fourier transform）来优化GFDM系统PAPR 性能。此外，文献[26-27]指出WFRFT在衰落信道中具有误码率性能优势。

目前，已有多篇文献独立且完整地提出了抑制GFDM 信号的OOB 辐射和降低PAPR 的方案，但只有少数文献研究了两者的联合抑制问题。为了实现对GFDM 系统OOB 和PAPR 性能的联合优化，本文基于频谱预编码（SP,spectral precoding）理论为GFDM 系统设计了一种通用预编码器。频谱预编码是一种重要的技术手段，通过优化信号的频谱分布，以实现对系统带外功率的抑制。通过研究GFDM 系统功率谱衰减特性，给出了预编码器的具体表达式，阐述了预编码器参数对GFDM 带外功率的影响，通过调节预编码器参数实现对GFDM 系统带外功率的调控。在此基础上，提出了基于WFRFT频谱预编码的GFDM（WFRFT-SP-GFDM）系统，通过二维参数的灵活配置，实现了带外功率、峰均功率比、误码率等性能的联合优化。

1 系统模型

1.1 GFDM 模型

GFDM 系统是一种针对时频资源进行调制的多载波传输系统，考虑一个具有K个子载波和M个子符号的GFDM 系统，发射端信源提供的比特信息通过正交幅度调制（QAM,quadrature amplitude modulation）得到码元信息，一个时频资源单位内包含的N个码元信息通过M个子符号进行传输，每个子符号包含K个子载波，即N=KM。第m个子符号上的码元信息记为dm=[d0,m,…,dK-1,m]T。GFDM 系统第k个子载波上的M个子符号通过原型滤波器循环卷积进行滤波，滤波后的信号经过上变频到第k个子载波，生成第k个子载波上的发射信号，通过K个子载波叠加形成的GFDM 信号为

根据式(1)，GFDM 系统调制过程的矩阵形式可以表示为

其中，d=[d0,0,…,dK-1,0,…,dK-1,M-1]T表示待传输码元信息，矩阵A为KM×KM阶调制矩阵，表示为

调制矩阵A由原型滤波器经过时移和频移形成，包含GFDM 信号调制过程中涉及的所有信号处理步骤。

1.2 WFRFT 模型

WFRFT 可以看作傅里叶变换的推广形式，即傅里叶变换是WFRFT 在某种情况下的特例。阶数为α的WFRFT 定义为

其中，x(n)为时域信号，x(-n)为时域反转信号，X(n)为频域信号，X(-n)为频域反转信号；ω0(α)、ω1(α)、ω2(α)和ω3(α)为WFRFT 的系数，定义为

其中，θ=0,1,2,3。另外，由于加权系数所具有的周期性，因此加权阶数α的取值范围通常为[0,1]。由式(4)可得，阶数为α的WFRFT 的矩阵形式为

其中，Wα为α阶加权分数傅里叶变换矩阵，表示为

其中，I表示单位阵，F表示傅里叶变换矩阵。当阶数α=0时，Wα简化为单位阵；当阶数α=1时，Wα简化为傅里叶变换矩阵。

2 WFRFT-SP-GFDM 系统模型

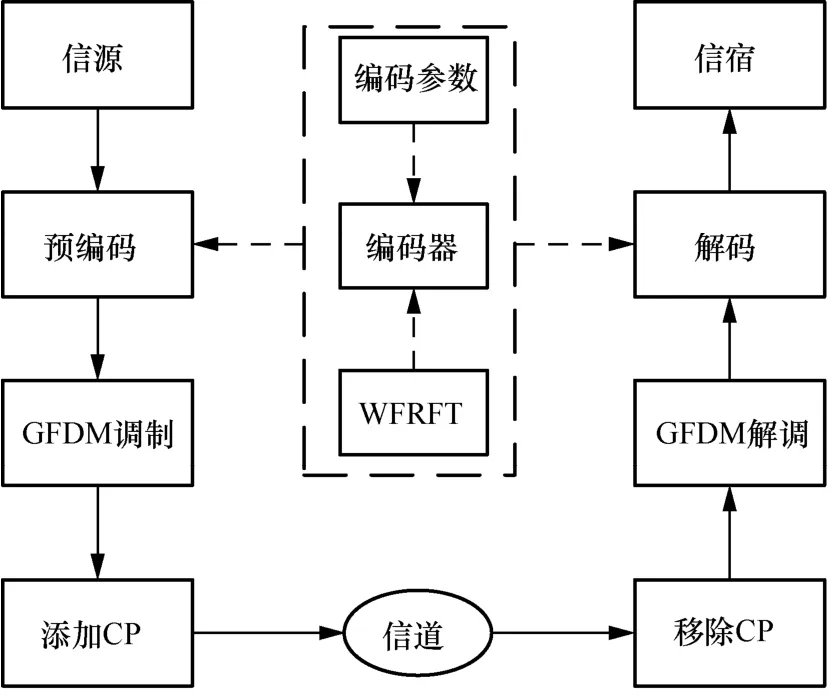
图1 WFRFT-SP-GFDM 系统框架

在预编码之后，每个子符号通过原型滤波器g(t)进行成型滤波并上变频，经过时域叠加后得到GFDM 信号，在一个GFDM 信号时间间隔T内，GFDM 信号可以表示为

其中，IM为M阶单位阵。当预编码矩阵U为单位阵时，SP-GFDM 系统简化为GFDM 系统。

SP-GFDM 信号基带的功率谱密度可以表示为

通过重复分部积分将式(11)展开为无穷级数

由式(15)可以得出，当预编码矩阵满足约束条件时，GFDM 系统的带外功率衰减速度为f-2J-2甚至更快。约束条件可以等价地改写为

并且预编码矩阵U满足UHU=I。在GFDM 系统调制传输过程中，考虑到每个子符号具有相似的谱特性，使GFDM 波形的谱特性呈现一定的规律性。为了方便分析，假设在GFDM 系统预编码和调制过程中，子符号携带具有独立同分布的码元信息，且满足E。因此可得SP-GFDM 系统功率谱密度的另一种表现形式为

其中，Gm(f)是e(f)gm(f)的傅里叶变换。作为多载波调制的一种方案，相对于单载波调制来说，GFDM 系统同样也面临着PAPR 较大的问题。PAPR较大时会导致功率放大器工作在非线性区域，引入了信号失真和频谱再生，影响功率谱的快速衰减。因此通过对GFDM 系统频谱预编码，达到带外功率快速衰减的同时也要考虑对PAPR 的抑制。为此将预编码器U扩展为预编码器UQ，并令P=UQ简化后续表述，通过预编码器P实现对GFDM 系统的带外功率和峰均功率比的联合优化。通过对Q加以设计，实现降低GFDM 系统PAPR 的同时保持带外功率快速衰减的特性，此时SP-GFDM 系统功率谱可以表示为

酉矩阵具有保持信号能量的性质，它可以有效地保持信号的功率不变。当Q矩阵是酉矩阵时，其不会影响SP-GFDM 系统带外功率的快速衰减。由式(22)也可得，当Q矩阵是酉矩阵时，其满足QQH=I，此时式(22)退化为式(21)，即Q为酉矩阵时不影响SP-GFDM 系统带外功率的快速衰减。值得注意的是，预编码矩阵P是一个K×S的矩阵，Q矩阵为S×S矩阵，用于在不改变所得功率谱的情况下降低GFDM 系统的PAPR。考虑到WFRFT预编码矩阵为酉矩阵且具有易与GFDM 系统结合的特性，并可以有效降低GFDM 系统的PAPR。因此，以此为切入点来研究Q矩阵的具体表达形式。定义一个K×S的矩阵为α阶加权分数傅里叶变换矩阵Wα删除前J列和最后J列的形式。为了实现降低GFDM 系统PAPR 的目的，将预编码矩阵逼近取得最小值，即约束条件为

在这种情况下，GFDM 波形与WFRFT 预编码的GFDM 波形具有相似性，从而实现在带外功率快速衰减的情况下降低系统PAPR。对约束条件进一步分析可得

由式(25)和式(26)可得优化后的结果为

WFRFT-SP-GFDM 系统的矩阵表示为

其中，J和α为预编码器参数。当预编码参数取特定值时，如表1 所示，WFRFT-SP-GFDM 可退化为不同的波形模态，在基于WFRFT 的通用预编码框架下，实现了WFRFT-SP-GFDM、WFRFT-GFDM、SP-GFDM、GFDM 等波形体制的融合。

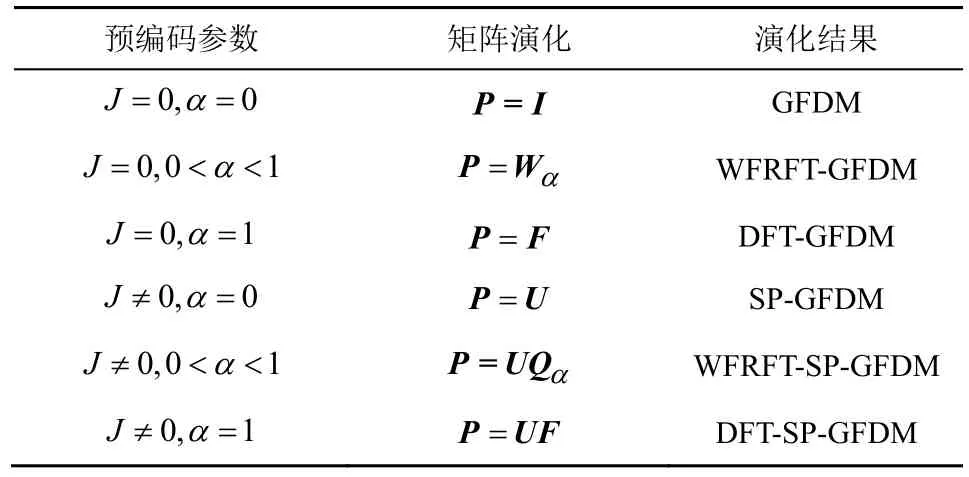
表1 WFRFT-SP-GFDM 参数等效关系

3 仿真结果与分析

为了验证WFRFT-SP-GFDM 系统的性能优势，本节对WFRFT-SP-GFDM 系统OOB、PAPR 和BER性能进行了仿真。表2 给出了WFRFT-SP-GFDM 系统仿真参数设定。

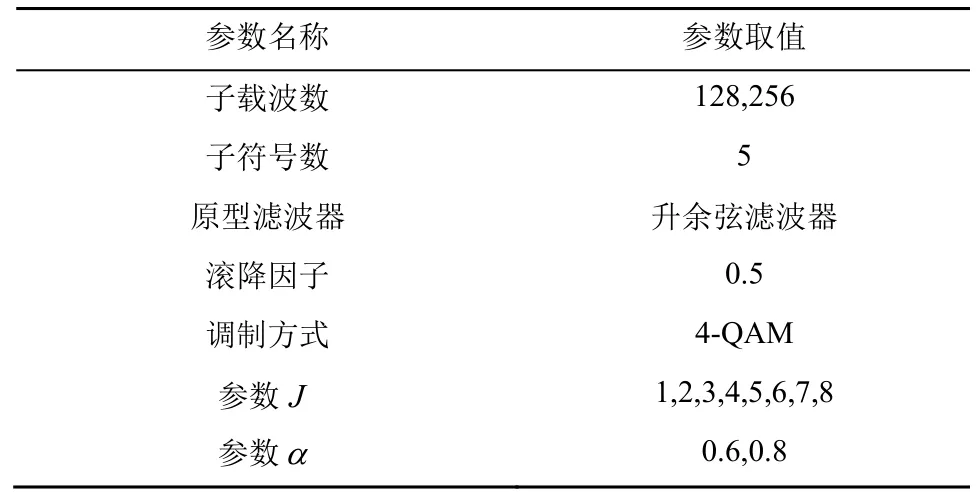
表2 WFRFT-SP-GFDM 系统仿真参数设定

3.1 带外功率性能

为了研究WFRFT-SP-GFDM 系统在带外功率快速衰减以及不同参数下的预编码器对带外功率影响的效果，对WFRFT-SP-GFDM 系统的OOB 性能进行了仿真分析。图2 给出了当子载波参数K分别为128 和256 时，随着参数J增大，WFRFTSP-GFDM 系统相比于GFDM 系统在子载波利用率所承受的具体损失。

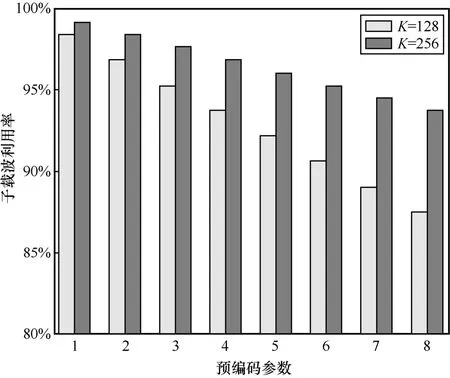
图2 WFRFT-SP-GFDM 系统子载波利用率

如图3 所示，与GFDM 系统相比，SP-GFDM系统带外功率泄露较低，即SP-GFDM 系统可以实现更快的带外功率衰减，而且参数J不同时的SP-GFDM 系统的带外功率衰减也有差异，即随着参数J的增大，衰减速率加快，证明了推导结果的正确性。如图4 所示，不同α参数下的SP-GFDM系统和WFRFT-SP-GFDM 系统的OOB 性能基本一致，即WFRFT-SP-GFDM 系统OOB 性能不受参数α的影响。相同参数J下 SP-GFDM 系统和WFRFT-SP-GFDM 系统OOB 性能具有一致性，验证了式(22)所指出的当Q为酉矩阵时不会影响GFDM 系统带外功率的性能。另外，图3 和图4 表明，当预编码参数J增大时，系统使用的子载波并未减少，仍为128 个子载波，即所有子载波均处于使用状态。这一结果表明，无论预编码参数J的取值如何，系统都能够充分利用所有子载波进行信息传输。总体而言，WFRFT-SP-GFDM 系统可以通过调节参数J来调控带外功率抑制性能，实现带外功率抑制和子载波利用率的折中，且比GFDM、WFRFT-GFDM 等波形具有更低的带外功率。

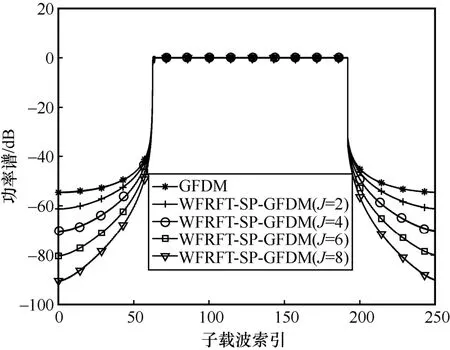
图3 SP-GFDM 系统带外功率性能

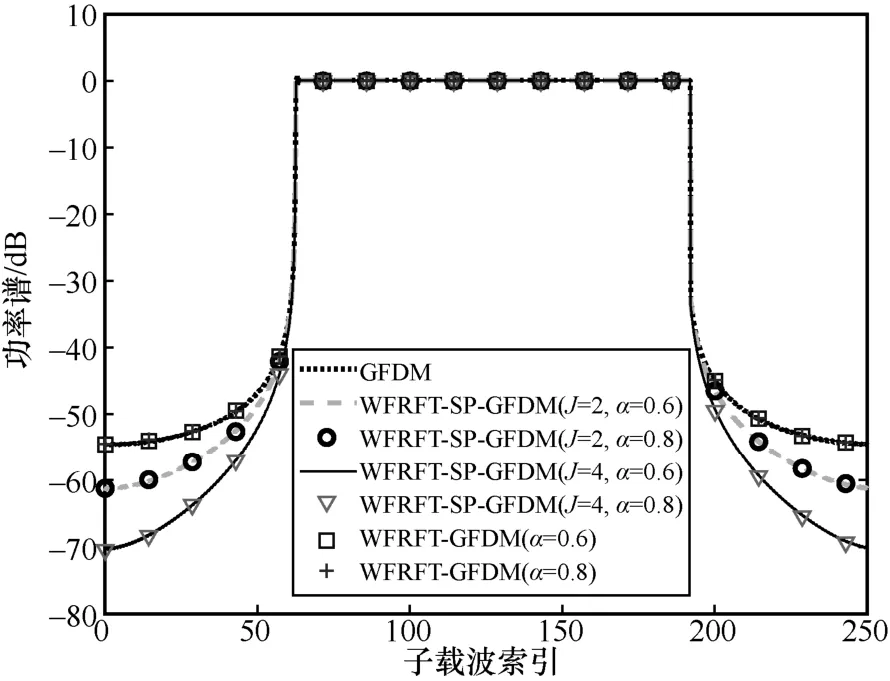
图4 WFRFT-SP-GFDM 系统带外功率性能

3.2 峰均功率比性能

为了研究预编码参数对WFRFT-SP-GFDM 系统PAPR 性能的影响，对WFRFT-SP-GFDM 系统PAPR 性能进行了仿真分析，仿真过程中采用4 倍过采样处理。

如图5 所示，其中，横坐标r0表示PAPR 门限值，纵坐标CCDF 表示系统大于对应PAPR 门限值的概率。SP-GFDM 系统的PAPR 性能与GFDM 系统的PAPR 性能相比基本一致，即U预编码对GFDM 系统的PAPR 性能有轻微的影响。参数α相同时，不同参数J下WFRFT-SP-GFDM 系统性能基本一致，即参数J不影响WFRFT-SP-GFDM 系统的PAPR 性能。参数J相同时，与GFDM 系统相比，不同参数α下WFRFT-SP-GFDM系统PAPR性能有所改变，且随着参数α的增大，PAPR 抑制效果逐渐增强。结合WFRFT-SP-GFDM 系统OOB 性能分析，通过矩阵U和矩阵Qα分别实现了对GFDM 系统的OOB 性能和PAPR 性能的调控，且两者具有不会相互作用影响的良好性质，通过调节参数J和α，实现GFDM 系统OOB 性能和PAPR 性能的协同控制。此外，当编码参数α相同时，WFRFT-SP-GFDM 系统的 PAPR 性能逼近于WFRFT-GFDM 系统PAPR 性能。

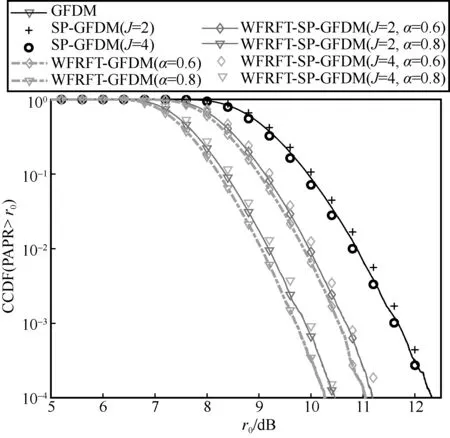
图5 WFRFT-SP-GFDM 系统峰均功率比性能

3.3 误码率性能

为了探究预编码参数对 WFRFT-SP-GFDM系统误码率的影响，对WFRFT-SP-GFDM 系统BER 性能进行了仿真分析。仿真中信道为AWGN信道和多径信道，其中，多径信道设置为6 条径，每条径的时延设置为[0,100,150,200,250,300]ns，每条径的平均功率设置为[0,-3,-6,-7.2,-10.8,-18,-25.2]dB。

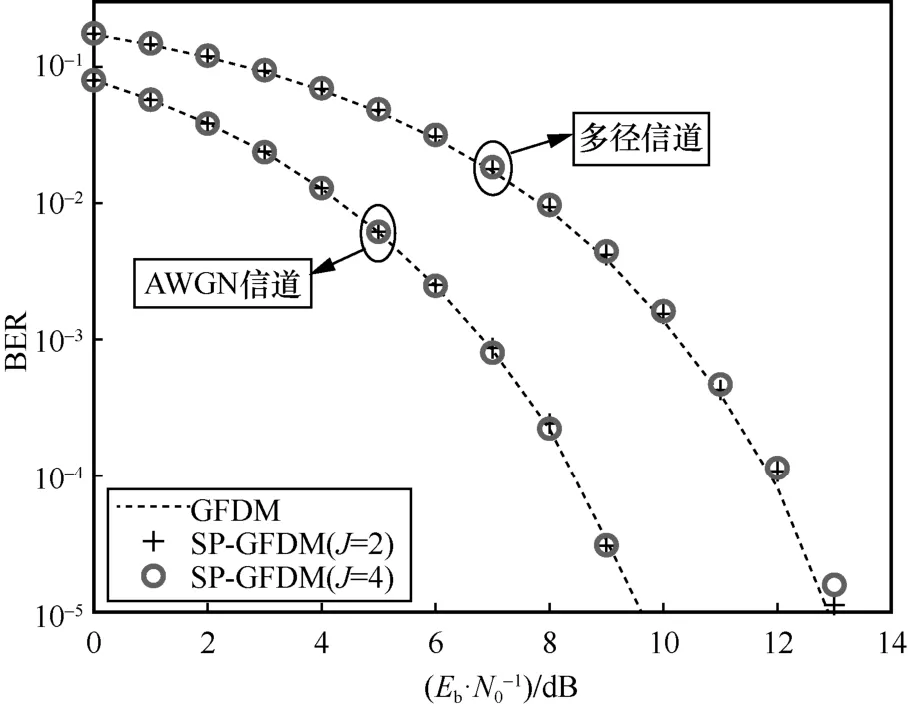
图6 SP-GFDM 系统误码率性能

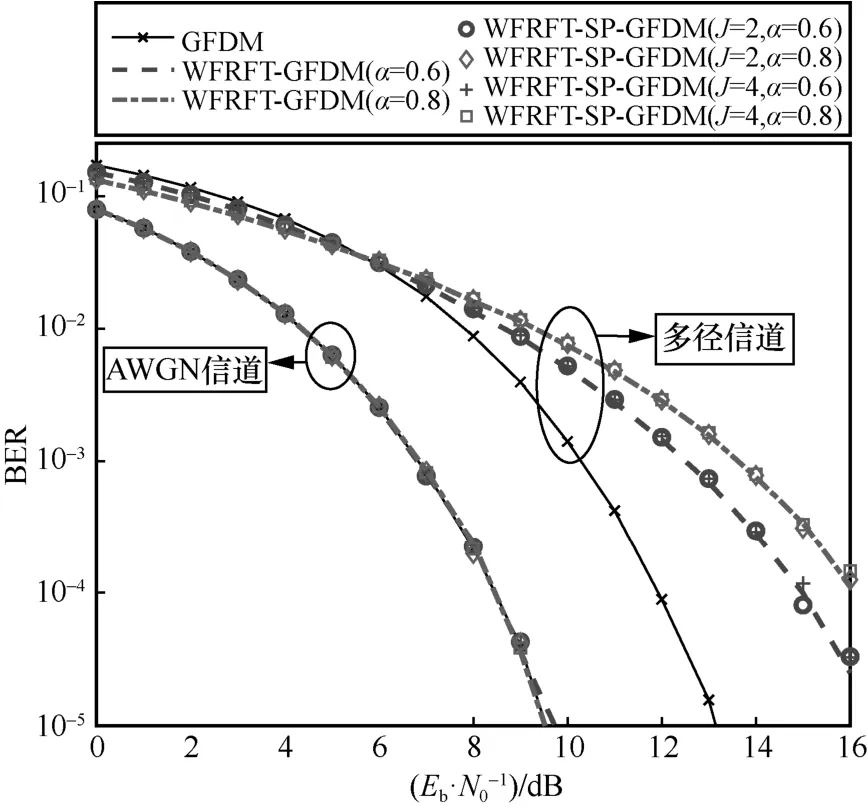
图7 WFRFT-SP-GFDM 系统误码率性能

4 结束语

本文面向通信波形的带外功率抑制需求，针对GFDM 系统的带外功率、峰均功率比、误码率等性能的联合优化问题，提出了一种基于WFRFT 的通用频谱预编码器。通过对SP-GFDM 系统功率谱衰减特性的理论分析，推导了使其快速衰减的约束条件，给出了预编码矩阵的具体表达式，详细论述了预编码参数对GFDM 系统带外功率衰减的影响机理。在此基础上，结合 WFRFT 理论提出了WFRFT-SP-GFDM 系统，通过二维参数的灵活配置，WFRFT-SP-GFDM 可退化为GFDM、SP-GFDM、WFRFT-GFDM 等波形，实现了对带外功率、峰均功率比等性能的灵活调控。仿真结果表明，WFRFT-SP-GFDM 系统实现了带外功率、峰均功率比、误码率、子载波利用率等性能的联合优化，与GFDM 波形相比，具有更低的带外功率和峰均功率比；与WFRFT-GFDM 波形相比，在峰均功率比和误码率性能近似相同时，具有更低的带外功率性能。