带肋铝合金管混凝土轴压短柱受力性能分析

陈冠君 黎明

苏州科技大学土木工程学院 215011

引言

众所周知，钢管混凝土组合柱具有承载力高、延性好、易于施工和节省成本等众多优点。国内外学者对不同受力情况、不同界面类型、不同构造参数以及不同改良方式的钢管混凝土结构进行了大量的试验、有限元模拟及理论研究。目前已经形成了比较完善的钢管混凝土结构理论体系。铝合金管混凝土可以有效地继承钢管混凝土的优点，而且铝合金材料能够在表面形成一层致密的防腐蚀氧化膜，从而大幅减少构件的维修维护成本。但关于铝合金管混凝土组合柱的相关研究仍然很少，对带肋的铝合金管混凝土研究仍然欠缺。

国内查晓雄和宫永丽［1，2］基于对试验和有限元结果的分析，并参考钟善桐的“统一理论”提出了圆铝合金管混凝土轴压短柱的承载力计算公式，建议了圆铝合金管混凝土轴压长柱的稳定系数计算公式。2016 年龚文志［3］对28 根不同参数的铝合金管混凝土长柱开展了受弯性能试验研究，并参考了国内外钢管混凝土结构设计规范的抗弯刚度计算公式，发现英国规范BS5400（2005）［4］的计算公式结果与试验结果最为接近，但离散程度比较大。2016 年，徐杰［5］进行了碳纤维缠绕后的圆截面铝合金管混凝土和方截面铝合金管混凝土组合柱受弯的试验研究和理论分析，进而对两种截面铝合金管混凝土组合柱的刚度、峰值荷载、破坏形态和延性进行了详细的研究。

国外只有Young Ben 对铝合金管混凝土轴压短柱进行了实验研究和理论分析。2009 年，Young Ben［6］对铝合管混凝土轴压短柱进行了试验研究，并且将试验所得结果与现有规范进行比较，提出现有规范对铝合金结构设计强度的计算偏于保守。2012 年，Young Ben［7］使用ABAQUS

软件对192 个不同参数的组合柱进行了分析，在对两者结果分析的基础上提出了铝合金管混凝土短柱承载力的计算公式，其计算结果与试验结果更为接近。

本文旨在研究带肋铝合金管混凝土轴压短柱的受力性能。对具有不同强度核心混凝土、不同加肋个数的铝合金管混凝土进行一系列的有限元模拟，对模拟结果进行分析研究并与理论计算值进行比较分析，在此基础上给出铝合金管混凝土轴压短柱的建议计算公式。

1 有限元建模与验证

1.1 基本信息

如表1 所示，共设计了9 根带肋铝合金管混凝土轴压短柱，加肋个数0～8、混凝土强度等级C30～C70，含铝率0.066～0.083。表1 中试件编号的含义：C30、C50、C70 代表试件核心混凝土强度等级，后面的数字0、4、8 代表铝合金管加设纵肋的个数。为了避免试件发生细长柱的整体屈曲破坏，所有试件初始高度与截面直径比均为3。具体的试件模型如图1 所示。参考文献［6］中进行铝合金管混凝土试验研究选取了2mm～5mm壁厚，本文主要探究加肋对薄壁构件的受力性能影响，故取壁厚为2.5mm，肋厚与壁厚相同。为了方便实际工程设计，肋宽取自铝合金管外直径的1／10，后续有待开展不同肋宽与外径比例的试件研究。

图1 有限元模型细节Fig.1 Details of finite element model

表1 试件设计汇总Tab.1 Summary of test piece design

1.2 单元类型和网格

铝合金管和混凝土的元素类型从ABAQUS的元素库中进行选择，实体单元能够满足计算所需的精度并且计算效率高，因此铝合金管和混凝土均采用8 节点线性减缩积分实体单元（C3D8R）。采用结构化网格划分技术进行网格划分。

1.3 材料的本构关系

1.铝合金的本构关系

采用有限元软件ABAQUS内部的等向弹塑性模型来建立铝合金材料模型。分析后发现，Ramberg-Osgood模型［8］能很好地拟合铝合金单轴受拉应力-应变曲线。因此，采用该模型作为铝合金的单轴本构关系，如下所示：

式中：σa、εa分别为铝合金材料的应力和应变；Ea为铝合金材料的弹性模量。铝合金材料的弹性模量取74000MPa，泊松比取0.33，指数n 采用斯坦哈特（steinhardt）建议来计算。

2.混凝土的本构关系

采用有限元软件ABAQUS内部提供的塑性损伤模型来建立核心混凝土的本构关系模型。刘威［9］在韩林海等学者研究的基础上，分析了核心混凝土受力特点并基于大量计算研究分析，最终提出建立核心混凝土模型时适用的模型。本文采用该模型作为核心混凝土的本构关系，如下所示：

1.4 界面接触定义

对于铝管和混凝土之间的界面，接触单元选择“面-面接触”。原则上规定刚度较大的部件为接触主面，因此以铝管内面单元为主面，混凝土单元为从面。其中，切向选择“罚摩擦”选项，并设置摩擦系数为0.25。法向选择“硬接触”选项，允许接触分离。

1.5 边界条件和加载方式

除了加载端（即顶面）施加纵向位移，组合柱顶面其他自由度和底面所有自由度均加以限制。采用位移控制方法对带肋铝合金管混凝土柱进行分析。通常，规定的位移为20mm。

1.6 模型验证

为了验证有限元模拟的准确性，根据文献［10］中的铝合金管混凝土（CAC-4）实际参数进行模拟，试件的几何参数为：直径150mm、壁厚5mm、长450mm，核心混凝土强度等级为C40，铝合金牌号为6061-T6，将模拟结果与试验结果进行对比，如图2 所示。由图中可见，组合柱的模拟曲线与试验曲线呈现出相同的起伏趋势，模拟的极限承载力与试验值偏差6.5%，证明了有限元模拟的可行性。

图2 有限元模拟与文献试验数据对比Fig.2 Comparison of finite element analysis and literature test data

2 有限元计算结果分析

2.1 试件的荷载-位移关系分析

本文以铝合金管加肋个数和核心混凝土强度为基本参数，利用建立的有限元模型，对带肋铝合金管混凝土的承载能力进行分析。图3 为有限元分析得到的试件典型变形，展现了试件达到峰值荷载后发生鼓曲型破坏的特征。图4（a、b、c）展示了核心混凝土强度不同对试件荷载-位移关系的影响，为了探究核心混凝土强度不同对试件延性的影响，采用文献［11，12］使用的延性系数公式，公式如下所示：

图3 有限元模拟典型变形Fig.3 Typical deformation diagram of finite element simulation

图4 荷载-位移关系曲线Fig.4 Load-displacement relationship curve

式中：DI为延性系数；u85%为荷载下降至极限荷载的85%时（峰值后）所对应的位移值；u75%为荷载上升至极限荷载的75%时（峰值前）所对应的位移值。

表2 汇总了试件的峰值荷载和延性系数。由图4（a、b、c）和表2 可以看出，在加肋个数不变的情况下，增加试件的核心混凝土强度可以大幅提升试件的极限承载力，同时也会导致试件的延性有所下降。

表2 试件峰值及延性系数汇总Tab.2 Summary of peak value and ductility coefficient of test piece

图4（d、e、f）展现了不同加肋个数对试件荷载-位移曲线的影响。由图4（d、e、f）和表2 可以看出，对于核心混凝土强度为C30 的试件，带4 肋试件相较于无肋试件峰值荷载提高了7.6%，带8 肋试件相较于带4 肋试件峰值荷载提高了6.5%；对于核心混凝土强度为C50 的试件，带4肋试件相较于无肋试件峰值荷载提高了4.6%，带8 肋试件相较于带4 肋试件峰值荷载提高了4.1%；对于核心混凝土强度为C70 的试件，带4肋试件相较于无肋试件峰值荷载提高了3.6%，带8 肋试件相较于带4 肋试件峰值荷载提高了3.8%。由此可见，铝合金管内部加设纵肋能够有效提升组合柱的整体承载能力和延性，同时随着核心混凝土强度的提升，加设纵肋对试件整体极限承载力提升的幅度会有所下降。

2.2 试件的应力分析

图5 展示了强度为C30 的核心混凝土纵向应力云图。从图中可以发现，加设4 根肋试件与无肋试件相比核心混凝土的纵向应力有所提升，加设8 根肋试件比加设4 根肋试件相比核心混凝土的纵向应力也有所提升。铝合金管混凝土轴压短柱在轴向压力作用下，组合柱上下顶端保持为平面，外部铝合金管与核心混凝土共同承受轴向压力作用而产生轴向压缩变形，铝合金材料的横向变形系数在弹性阶段变化较小，但从弹性阶段快进入塑性段时，铝合金的横向变形系数会迅速增加到一个定值，然后在屈服平台阶段材料泊松比保持不变。混凝土材料的横向变形系数会随着轴向压应力的增加而持续增大，直至超过铝合金材料的横向变形系数。研究表明，当外部铝合金管的轴向压应力接近比例极限时，外部铝合金管的横向变形系数开始小于核心混凝土的横向变形系数，此时核心混凝土的横向变形开始受到外部铝合金管的约束，外部铝合金管与核心混凝土之间出现相互作用力。此时，核心混凝土处于三向受压状态，外部铝合金管也处于三向受力状态（纵向受压、径向受压和环向受拉）。在铝合金管内部加设纵肋后，可以延缓铝管局部屈曲的发生，从而提升铝管对核心混凝土的约束作用，混凝土的径向压力会随之增大，由力的平衡条件可得混凝土的纵向压力也会随之增大。这个现象说明在铝管内部加设纵向肋能够有效增强外部铝管对核心混凝土的约束效果。

图5 C30 核心混凝土纵向应力云图（单位：MPa）Fig.5 Cloud Chart of Longitudinal Stress of C30 Core Concrete（unit：MPa）

图6 为典型C30 系列试件外部铝合金管的Mises应力云图。在截取应力云图时为了确保对比的可靠性，截取了试件达到峰值荷载时的应力云图，并且设置了相同的应力上下限。由图可见，无肋铝管最高应力集中在高度中部位置，4肋铝管最高应力分布区域有所扩大，8 肋铝管最高应力分布区域最大。由此可见，加设纵向肋的试件与无肋试件相比，铝管整体的应力分布更加均匀。此现象说明加设纵向肋可以延缓铝管发生局部屈曲，从而有效地增强铝管对核心混凝土的约束效果，提升试件整体承载能力。

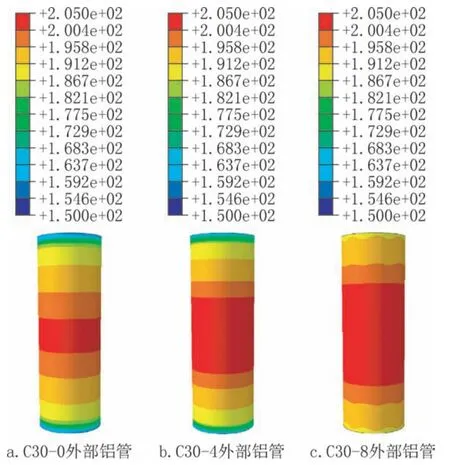
图6 铝合金管Mises 应力云图（单位：MPa）Fig.6 Mises stress nephogram of aluminum alloy pipe（unit：MPa）

3 理论计算

3.1 理论计算与有限元模拟结果对比分析

目前国内外关于铝合金管混凝土计算理论的研究尚不充分，钢管混凝土的计算理论有很多，主要有三种理论：套箍理论、统一理论和叠加理论。套箍理论是由蔡绍怀［13］学者最先提出的。目前使用该理论计算钢管混凝土轴压短柱极限承载力的设计规程主要有《钢管混凝土结构技术规程》（CECS 28—2012）［14］和《高强混凝土结构技术规程》（CECS 104：99）［15］等。统一理论是由钟善桐［16］学者最先提出来的，计算过程中将钢管混凝土组合柱整体视为一种新型的组合材料，来计算组合柱的整体承载力。目前使用该理论的设计规程主要有《钢-混凝土组合结构设计规程》（DL／T 5085—1999）［17］、《高层建筑钢-混凝土混合结构设计规程》（DG／TJ08-015—2018）［18］等。叠加理论把外部钢管与核心混凝土的承载力按照一定的比例进行叠加，来作为钢管混凝土组合柱整体的极限承载力。目前使用该理论的设计规程有国外一些具有代表性的钢管混凝土结构设计规程，如欧洲规范EC4（2004）［19］、美国规范ACI（2005）［20］、日本规范AIJ（1997）［21］。

目前国内外仅有少量的关于铝合金管混凝土结构的设计规范，并且现行的铝合金管混凝土相关规范中的计算理论也是借鉴钢管混凝土的叠加理论，文献［6］采用澳大利亚／新西兰［22］和美国的铝合金设计规范［23］按照公式计算铝合金管混凝土的轴压承载力。

为计算铝合金管混凝土短柱的轴压承载力，参考国内外对于钢管混凝土轴压承载力的计算理论，将钢管混凝土中的钢管替换为铝合金管，并对其进行计算验证，见表3。将ACI（2005）关于钢管混凝土计算公式中的钢材替换为铝材后，计算公式的形式与上述澳大利亚／新西兰和美国的铝合金设计规范相同，因此表3 中取ACI规范为两者代表进行对比分析。

表3 试件有限元模拟值与计算值比较Tab.3 Comparison of finite element simulation value and calculated value of test piece

由表3 可得，套箍理论考虑在轴向压力作用下外钢管对核心混凝土产生套箍作用，使混凝土处于三向受力状态，从而使整体强度大幅提高，计算结果略低于有限元模拟结果。基于统一理论的韩林海计算公式［24］和钟善桐计算公式的计算结果与有限元模拟结果最为接近，吻合度较高。规范ACI、AIJ和EC4 中关于钢管混凝土的计算公式将钢管和核心混凝土两部分承载力的简单叠加作为钢管混凝土构建整体的承载力，这种叠加理论没有考虑外部钢管约束对于核心混凝土承载力提升的作用，计算值低于有限元模拟值。

3.2 带肋铝合金管混凝土建议计算公式

基于上文理论计算结果与模拟结果的对比分析，可知韩林海公式计算结果与有限元模拟结果最为吻合，可用于计算无肋铝合金管混凝土轴压短柱承载力。韩林海计算公式如下：

式中：As为外管截面面积；Ac为核心混凝土截面面积；Asc为组合截面面积；fs为钢材强度设计值；fc为核心混凝土的强度设计值。

目前国内外没有关于带肋铝合金管混凝土轴压短柱承载力的计算规范。因此，本文在有限元模拟分析的基础上，参考韩林海公式，对其中套箍系数ξ修正为ξr：

式中：Ar为加劲肋截面面积。将ξr带入原公式中得出带肋铝合金管混凝土修正计算公式：

用该公式对带肋铝合金管混凝土轴压短柱极限承载力进行计算，并与模拟结果进行对比，如图7 所示。

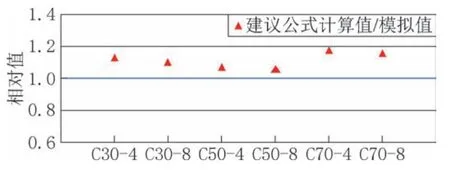
图7 建议公式计算结果与模拟结果比值Fig.7 Comparison of recommended formula calculation results with simulation results

图7 可见，建议公式计算值均大于模拟值，出现此现象是由于式（13）是在韩林海公式基础上进行修正，而韩林海公式充分考虑了钢管与混凝土之间相互作用对试件承载力的提升效果。另一方面，将公式中钢材替换为铝材后，铝材的弹性模量比钢材要小，公式中未考虑弹性模量的降低，所以在对比结果中呈现出计算值均比模拟值偏高，但平均误差为10%，在合理误差范围内。综上所述，采用本文建议公式计算带肋铝合金管混凝土轴压短柱承载力，具有一定的参考意义。

4 结论

本文通过对带肋铝合金管混凝土短柱进行非线性有限元模拟与理论分析研究，得到以下结论：

1.无肋铝合金管混凝土轴压短柱及带肋铝合金管混凝土轴压短柱的破坏形态均为鼓曲型破坏，构件中部发生鼓曲，保持较好的整体性。

2.核心混凝土强度的提升会使带肋铝合金管混凝土的极限承载力有所提升，但延性会有所降低。在铝管内部加设纵肋可以有效延缓铝管的局部屈曲，进而增强外部铝管对核心混凝土的约束作用，使组合柱的极限承载力和延性均得到提高。

3.基于统一理论的韩林海计算公式和钟善桐计算公式与有限元模拟结果最吻合，在韩林海公式的基础上，提出了带肋铝合金管混凝土轴压短柱的建议计算公式。