基于负时滞控制有效性的车辆坡道预见性驾驶*

刘灿昌 孙亮

(山东理工大学 交通与车辆工程学院,淄博 255049)

引言

预见性变速巡航控制策略通过变速巡航及整车节能控制,利用路径预见进行车辆前方路况重建,对车辆前方行驶道路下的动力需求进行预见性地定量分析.通过预见性整车坡道控制策略,对车辆整车动能、整车势能等多种能量进行管理,有效节省车辆燃油消耗,提高无人驾驶的适应性,降低能源消耗、改善生态环境.

基于速度和平稳的加减速驾驶行为研究成为当前研究的热点问题之一.预见性生态驾驶策略能有效较少汽车油耗[1-4].Ma等研究车队的燃油消耗,设计了一种简化的启发式算法,此方法用在智能网联车上将会减少大约 29%的燃油消耗[5-6].He等研究了车流自适应驾驶策略,该方法能有效地减少交通流的振荡和燃油消耗[7-8].

模型预测控制具有较强的处理多目标优化及约束的能力,得到广泛的应用[9-10].Li等结合驾驶员特性,利用模型预测控制算法设计间距控制器[11].Naus等设计基于模型预测控制算法的多目标优化策略,使车辆在满足车辆跟随性、乘坐舒适性等前提下,有效地提高了燃油经济性[12].张德兆等基于滚动时域的模型预测控制方法设计弯道条件下的自适应巡航控制算法,实现了横纵向协调控制[13].张亮修等利用模型预测控制算法综合协调车辆跟随时的跟踪性能、燃油经济性、乘坐舒适性以及行驶安全性,实现自车对前车良好的跟踪[14].

目前,最优经济性驾驶策略成为节能驾驶研究的重要问题之一.Saboohi 等[15]采用最优速度和档位控制方法,在交通流量较大的情况下可以节油1.5L/100km.Chang等[16]将车辆阻力看作速度的函数,将油耗看作行驶阻力的函数,给出巡航工况下常速最优策略.Mensing 等[17]使用动态规划方法求解给定轨迹和约束情况下的最优速度.Li 等[18]通过伪谱法研究无极变速器和机械式自动变速器车辆最优化的加速-滑行策略,并从机理上证明了其节油原理.但是,以上方法在建模过程中对车辆及道路的物理特性进行了简化,难以反映真实的车辆行驶状态和环境.此外,该方法对约束条件的精确度要求较高,实际操作中难以实现.

本文以无人驾驶汽车整车控制技术为研究对象,基于车辆智能网联技术,以负时滞作为未来路况预测参数,建立车辆坡道行驶的预见性驾驶动力学模型,解决传统的应激性整车控制策略面临的诸多瓶颈问题,为进一步提高无人驾驶汽车性能提供理论及实践指导,并为车辆智能节能驾驶奠定理论基础.负时滞控制参数的引入能够根据当前的驾驶行为的规划未来驾驶状态,提升无人驾驶车辆速度控制的适应性,同时能减少油耗,达到节能减排的目的.

1 车辆预见性驾驶建模分析

车辆坡道行驶的预见性驾驶模型如图1所示.考虑车辆爬坡驾驶工况,车辆离坡道起点的距离为l,坡道倾角为θ,高度为h,车辆目前的位置坐标为x(t),坡顶的位置坐标为x(t+τ),其中,τ为负时滞,表示车辆从目前位置到达坡顶所用时间,其数值由坡道前距离、坡道水平长度和车速确定.为节约能量和提高车辆行驶速度的平顺性,坡道前的控制策略通常采用上坡前提高车速,增大整车动能,减小爬坡油门开度和挡位的变换频率并能保持恒速.采用的控制策略是在水平坡道行驶中采用加速控制,油门控制开度与坡道高度成正比.下坡采用坡前减速,采用的控制策略是在水平坡道行驶中采用减速控制,油门控制开度与坡道深度成正比.但是,坡道前如何确定最优的加速距离?坡前加速速度多少能够有效节省爬坡能量? 为解决该问题,建立车辆坡道动力学模型,采用速度控制参数与坡道高度线性相关的控制策略,提高坡道前速度.坡道前变速行驶的动力学方程可以写为

图1 车辆预见性驾驶坡道模型Fig.1 Vehicle predictive driving ramp model

(1)

其中,m为车辆质量,c为速度阻力系数,F为恒速牵引力,Fr为路面恒定阻力,k为预见性控制系数,h为坡道的高度.式中,加号表示上坡控制,减号表示下坡控制.以下仅以上坡为例进行分析,下坡控制分析也采用相同的分析方法.坡度高度可以表示为

h=tanθ[ax(t+τ)-bx(t)-l]

(2)

其中,θ为坡道倾斜角度,l为车辆在t时刻与坡底的距离,a为转弯系数,b位移系数,τ为负时滞.方程(1)写为

ktanθ[ax(t+τ)-bx(t)-l]

(3)

方程(3)进一步化简得到:

(4)

将坡道前变速行驶的动力学方程(4)中的x(t+τ)按Maclaurin级数展开如下:

(5)

取式(5)前三项并将其代入式(4)可得:

+gbx+gl-f=0

(6)

令,则式(6)可进一步化简为:

(gb-ga)x(t)+gl-f=0

(7)

2 车辆上坡的控制有效性分析

车辆坡道行驶或者跟驰前方车辆时,需要保持足够的安全距离且速度不会降低直至停车,为此提出控制有效性概念,以满足车辆跟驰需要.

动力学系统在控制力和非周期激励合力作用下,克服阻力作用,位移从一个点随着时间变化指向另一个点,并随着时间增加不断增大,当时间趋于无穷大时,其位移也趋于无穷大.例如:质点在恒力作用下会一直加速运动下去,其位移不断增大.

动力学系统在控制力和非周期激励合力作用下,当合力趋于零时,动力学系统在接触阻尼作用下停止,并其位移从一个点随着时间变化不断指向另一个点,并随着时间增加不会无限增大,当时间趋于无穷大时,其位移也趋于一定值.

动力学系统在控制力和非周期激励合力作用下,其位移从一个点随着时间变化不断指向另一个点,并随着时间增加不会无限增大,当时间趋于无穷大时,其位移为零,返回出发点.例如:质点在控制力和非周期激励合力,其位移为零,返回原点.

定理1 对于一个含有控制参数非周期牵引力作用的动力学系统,其特征方程特征根均具有正实部,则称该控制系统是有效性控制系统.

(8)

设坡道前变速行驶的动力学方程(9)解为

y=Aeλt

(9)

当动力学系统特征方程特征根均具有正实部时,方程解的极限为

(10)

因而该控制系统是有效性控制系统.

推论:对于一个含有控制参数非周期牵引力作用的动力学系统,若特征方程特征根均具有正实部,则称动力学系统位移和速度恒为正.

定理2 对于一个含有控制参数非周期牵引力作用的动力学系统,其特征方程特征根具有零实部,则称该控制系统是渐进有效性控制系统.

定理3 对于一个含有控制参数非周期牵引力作用的动力学系统,其特征方程特征根均具有负实部,则称该控制系统是非有效性控制系统.

3 控制参数范围确定

设坡道前变速行驶的动力学方程(7)解为

x=Aeλt

(11)

坡道前变速行驶的动力学方程特征方程为:

(12)

由定理1和方程根的特性可知,坡道前变速行驶的动力学方程(9)有效控制条件为

(13)

(14)

一般情况下,上坡是一个加速过程,因而加速控制参数g>0.当b>a时,有效控制不等式(14)中分子g(b-a)大于零,因而分母1-1/2gaτ2须为正.不等式进一步写为

(15)

(16)

由不等式(15)和(16)中右端大小关系可知,当满足以下条件时

μτ<2

(17)

控制系统的有效性控制参数由不等式交集组成,与转弯系数、风阻系数和负时滞有关.当转弯、风阻系数一定时,加速控制增益随着负时滞增大而减小.车辆爬坡并要达到一定的冲坡速度时,如果加速控制增益变大,加速时间就会变小,反之,加速时间会变大.反之,当阻尼和负时滞满足以下条件时

μτ≥2

(18)

不等式(15)和(16)解集为空集,不存在有效控制参数.

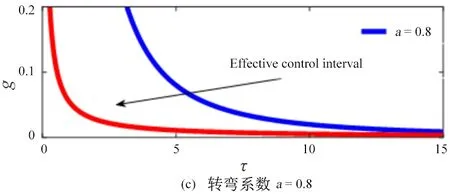
图2 上坡转弯系数对车辆上坡有效控制参数影响Fig.2 Influence of turning coefficient on effective control parameters of vehicle uphill

图2为转弯系数对有效控制参数影响关系图像.由图可知,有效控制参数由两个有效控制不等式组成,分别用红、蓝颜色实线表示,中间区域为有效控制区域,其余为非有效控制区域.在车辆上坡时,随着负时滞值的增加,不同转弯系数a值对应的控制增益g的最小值递减,且均收敛于零处.

图3为转弯系数对车辆上坡有效控制参数影响关系示意图.负时滞在稳定区域的较小区间内,随着转弯系数的增加,有效控制区域上界控制增益下降,而负时滞在稳定区域的较大区间和较小区域内,随着转弯系数的增加,有效控制区域下界控制增益基本保持不变.

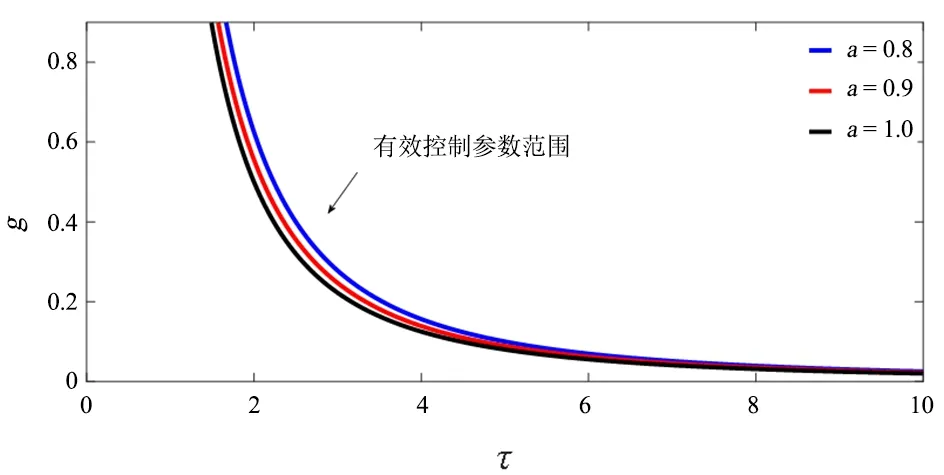
图3 转弯系数对车辆上坡稳定性控制参数影响Fig.3 Influence of turning coefficient on control parameters of vehicle uphill stability

图4为风阻系数对车辆上坡有效控制参数影响关系示意图.负时滞在稳定区域的较小区间内,随着风阻系数的增加,有效控制区域下界控制增益增大,而负时滞在稳定区域的较大区间和较小区域内,随着风阻系数的增加,有效控制区域下界控制增益基本保持不变.

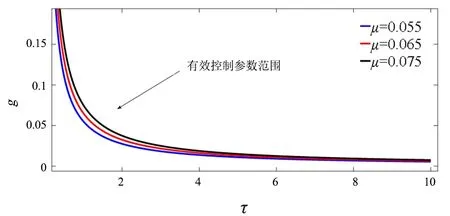
图4 阻尼对车辆上坡稳定性控制参数影响Fig.4 Influence of damping on control parameters of vehicle uphill stability

当b0.则由此可以推出约束条件(13-14)中分子gaτ-μ>0.即

(19)

(20)

显然,式(19)和式(20)无法同时满足,因而,该情况不存在有效控制参数.

由不等式(15)和式(16)中右端大小关系可知,当满足以下条件时

μτ>2

(21)

控制系统的有效性控制参数由不等式交集组成,与转弯系数、风阻系数和负时滞有关.当转弯系数、风阻系数一定时,加速控制增益随着负时滞增大而减小.车辆爬坡并要达到一定的冲坡速度时,如果加速控制增益变大,加速时间就会变小,反之,加速时间会变大.

反之,当阻尼和负时滞满足以下条件时

μτ≤2

(22)

不等式(15)和式(16)解集为空集,不存在有效控制参数

图5 动力学控制增益和油门开度的关系Fig.5 Relationship between dynamic control gain and throttle opening

图5坡道前变速行驶的动力学控制增益和油门开度的关系图.以k为横坐标,g为纵坐标绘制关系图如图3所示.对于同一道路坡度,g与a成正比例增加.

4 下坡有效控制参数确定

对于下坡工况,坡道前变速行驶的动力学方程(1)有效控制条件为

(23)

(24)

当g>0时,根据有效控制条件可知,约束条件式(18)中分子g(b+a)大于零。想要满足有效控制条件整体大于零,分母1+1/2gaτ2须为正.得到有效控制条件为

(25)

(26)

由不等式(25)和式(26)中右端大小关系可知,当满足以下条件时

μτ<2

(27)

反之,当阻尼和负时滞满足以下条件时

μτ≥2

(28)

不等式(23)和(24)解集为空集,不存在有效控制参数.

当g<0时,根据有效控制条件可知,约束条件式(24)中分子g(b+a)小于零.想要满足有效控制条件整体大于零,分母1+1/2gaτ2须为负.有效控制条件为

(29)

(30)

显然,式(29)和式(30)无法同时满足,因而,该情况不存在有效控制参数.

由不等式(23)和式(24)中右端大小关系可知,当满足以下条件时

μτ>2

(31)

控制系统的有效性控制参数由不等式交集组成,与转弯系数、风阻系数和负时滞有关.当转弯系数、风阻系数一定时,加速控制增益随着负时滞增大而减小.车辆爬坡并要达到一定的冲坡速度时,如果加速控制增益变大,加速时间就会变小,反之,加速时间会变大.

反之,当阻尼和负时滞满足以下条件时

μτ≤2

(32)

不等式(23)和(24)解集为空集,不存在有效控制参数.

图6为下坡时转弯系数对有效控制参数影响关系图像.由图可知,有效控制参数由两个有效控制不等式组成,中间区域为有效控制区域,其余为非有效控制区域.在车辆下坡时,随着负时滞τ值的增加,不同转弯系数a值对应的控制增益g的最小值递减,且均收敛于零处.

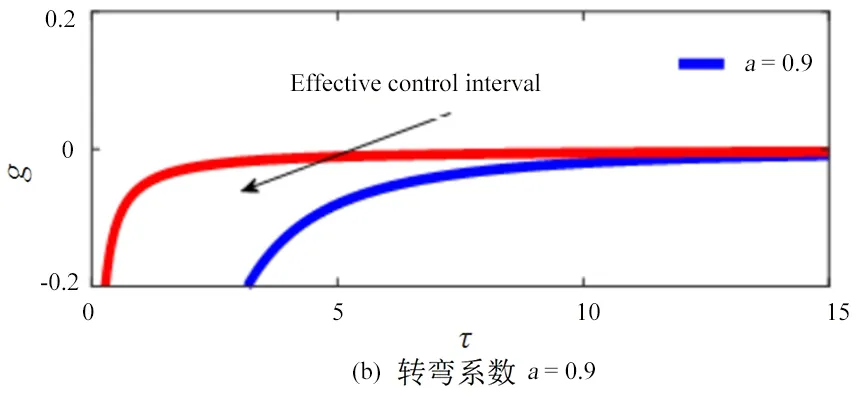
图6 上坡转弯系数对车辆上坡有效控制参数影响Fig.6 Influence of turning coefficient on effective control parameters of vehicle uphill

5 结论

建立车辆坡道动力学模型,分析加速控制参数与坡道高度关系规律,得到加速控制参数的有效范围,给出了车辆上坡控制的有效性定义和相关理论.控制系统的有效性控制参数由不等式交集组成,与转弯系数、风阻系数和负时滞有关.当转弯、风阻系数一定时,加速控制增益随着负时滞增大而减小.负时滞在稳定区域的较小区间内,随着转弯系数的增加,有效控制区域上界控制增益下降,而负时滞在稳定区域的较大区间和较小区域内,随着转弯系数的增加,有效控制区域下界控制增益基本保持不变.对于下坡工况,采用了类似分析方法.总之,选取合适的控制参数和时滞,可以有效设计冲坡(下坡)速度,减少油耗.