慢变参数激励Duffing系统中的延迟分岔现象及其诱发的簇发振荡*

魏梦可 韩修静

(江苏大学 土木工程与力学学院,镇江 212013)

引言

考虑如下慢变参数激励下的Duffing系统

(1)

其中,δ>0且γsin(ωt)是正弦参数激励. 针对系统(1)或其他类似的非线性模型的动力学行为,学者们展开了一系列的研究,并已经取得了一些重要的结果,例如参见文献[1-4]. 然而,目前相关研究大多集中在常规参数激励下的情况,即ω=o(1).针对慢变激励驱动下Duffing系统的动力学行为却鲜有研究.本文将聚焦于这一情形,主要研究当ω=o(ε)(0<ε≪1)时,慢变参数激励下Duffing系统的动力学. 由于ω很小,系统(1)可以视为一个两尺度耦合的非线性系统,即激励频率和系统的固有频率之间存在量级差异.

延迟分岔行为,如延迟Hopf分岔[5,6]、延迟叉型分岔[7,8]和延迟鞍-结分岔[9,10],引起了研究人员的广泛关注和强烈兴趣. 所谓延迟分岔,又称为慢过效应或记忆效应[5],是吸引子的一种延迟失稳现象,即当吸引子失稳变成排斥子时,系统的轨线继续在排斥子上停留一段时间,然后再离开排斥子的现象. 这种延迟效应已经成为可以诱发簇发振荡[11-14]的有效机制之一,即其诱导的动力学行为通常表现为在每一演化周期中大幅振荡与小幅振荡交替出现[15].

与延迟分岔相关的研究成果虽然很多,但主要是针对慢变参数是时间的线性函数的情形. 这里我们所考虑的参数激励的Duffing系统(1)是一个慢变参数激励是时间的非线性函数的系统. 线性控制参数只能通过分岔点一次,相关的延迟行为受初始时间的影响很大[16-19]. 而对于慢变参数激励,由于它是一个周期性的函数,它将周期性地通过分岔点,因此周期性的延迟行为可能发生.

针对簇发振荡中的周期性延迟分岔现象,目前已经取得了一些研究成果. 例如,在之前的工作中,我们探讨了在周期外激励作用下的van der Pol系统中鸭式爆炸延迟所导致的簇发振荡[20];分析了慢变参数激励van der Pol系统中的延迟Hopf分岔现象,给出了近似计算簇发中的连续尖峰的数目的方法[21];研究了一类电路系统中基于延迟Hopf分岔通向簇发振荡的两条不同路径,并定性分析了不同初值下系统的轨迹,结果表明从长时间来看,簇发振荡中的延迟行为并不受系统初值的影响[22];揭示了簇发振荡中周期性延迟分岔的动力学特性,报道了多种由延迟分岔诱导的簇发振荡[23].

关于延迟时间的计算,现有的文献大多仅考虑了首次延迟分岔行为的延迟时间,针对整个周期性的延迟行为的延迟时间计算问题鲜有研究. 本文将主要研究系统初始时间对每次延迟行为的延迟时间的影响. 此外,还将分析延迟分岔行为对簇发振荡的产生所发挥的作用. 本文的其余部分安排如下. 在下一节中,通过引入慢时间尺度,将参数激励的Duffing系统转化为快-慢系统. 然后,得到相关的稳定慢流形和慢变平衡解. 第2节介绍簇发振荡和相关的动力学机制,分析初始时间对与簇发振荡中每次延迟行为的延迟时间的影响. 此外,简要分析簇发振荡的分类和演变. 最后,总结全文.

1 稳定慢流形和慢变平衡解

首先,引入慢时间尺度τ=ωt,然后可以得到系统(1)可以写成如下的快-慢形式

ωx′=y

(2a)

ωy′=(γsinτ)x-x3-δy

(2b)

τ′=1

(2c)

其中“′”代表关于慢时间尺度τ的导数,(x,y)是快变量,它们构成了一个由方程(2a)和(2b)给出的快子系统. 当快子系统中ω=0,可以得到

0=y

0=(γsinτ)x-x3-δy

(3)

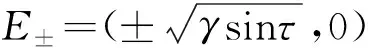
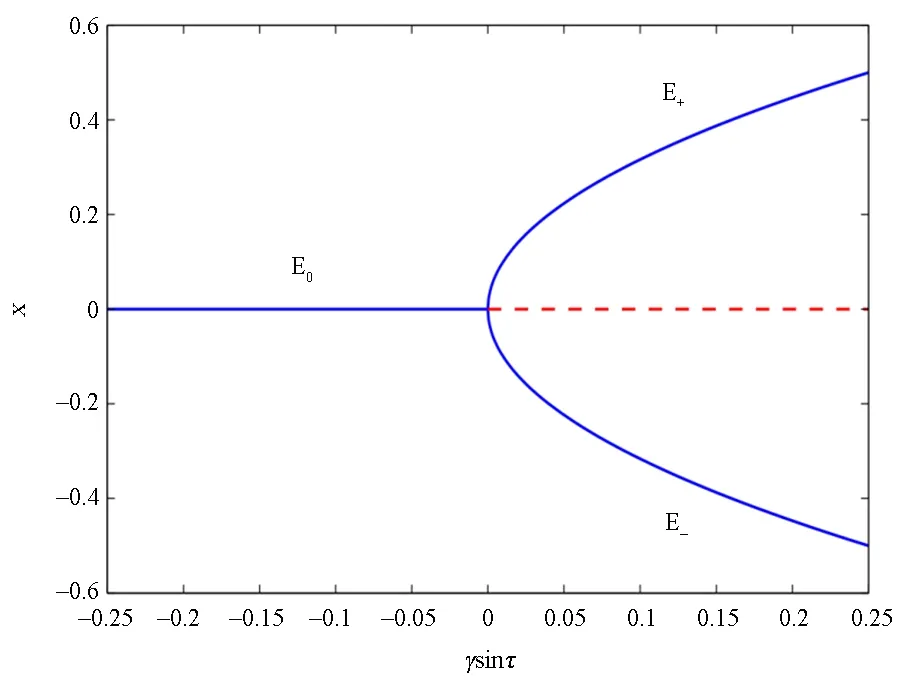
图1 快子系统中的叉型分岔,其中γsinτ是分岔参数,实线表示稳定的平衡点,虚线表示鞍点Fig.1 Pitchfork bifurcation of the fast subsystem, where γsinτ is chose as the bifurcation parameter. Solid lines mean sinks, while dashed line indicates saddle

基于上述分析,可得稳定慢流形Ms

Ms=M0∪M+∪M-

(4)

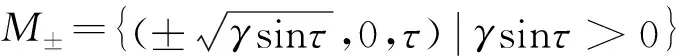
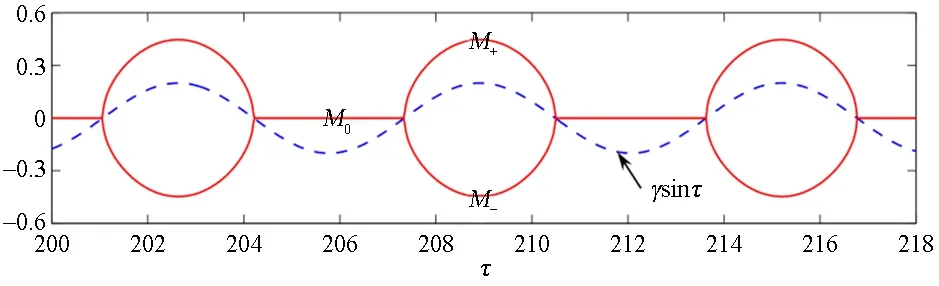
图2 当固定参数γ=0.2时,稳定的慢流形M0和M±(红线)和慢变参数激励γsinτ(蓝色虚线)的数值模拟Fig.2 Numerical simulations of the stable slow sub-manifolds M0 and M± (red solid curves) and the slow parametric excitation γsinτ (blue dashed curve), for the flxed parameter γ=0.2

一般地,当0<ω≪1时,慢流形M0和M±不是系统(2)的解.然而,根据准稳态假设,存在一个缓慢变化的平衡解,即流形Ms的一个小扰动,以ω阶的距离与流形Ms一起移动.当γsinτ<0时,缓慢变化的平衡解可以用M0来近似,并可满足关于ω的渐近级数. 通过使用Berglund[19]提出的方法,可以计算出该渐近级数

x0=o(ω2),y0=o(ω2)

(5)

但当γsinτ>0时,缓慢变化的平衡解可以用M+或M-来近似,并且满足以下关于ω的渐近级数

(6)

但是,在叉型分岔值0附近,解一般不会以ω阶的距离追随流形Ms,而是在ω的某个其他幂级距离处[19].

2 叉型分岔的延迟效应和簇发振荡的分类

基于上述分析,本节将研究当0<ω≪1时系统(2)中簇发振荡的产生机理.在本节,我们固定参数γ=0.2,ω=0.01,并将δ视为控制参数.

当δ=0.1时,图3(c)展示了系统(2)中的簇发振荡,其中慢流形Ms也被叠加在一起,以便清楚地了解相关的转迁机制. 此外,图3(a)给出了与簇发振荡相对应的传统相图. 为了清晰地展示簇发振荡中的分岔机制,图3(b)给出了与簇发振荡相关的转换相图[24,25]与图1所示的快子系统的分岔图的叠加图.

正如图3(b)和图(c)所示,当0.2sinτ<0,慢流形M0是稳定的且系统轨线跟随M0.当0.2sinτ增大并穿越临界值0时,发生了一个有趣的现象,即延迟分岔,也被称为延迟失稳.当0.2sinτ>0时,M0失稳.然而,在系统轨线跳到慢流形M+或M-之前,先是跟随不稳定的慢流形M0一段时间(即,延迟时间).这种延迟行为导致了M0和M+/M-之间的滞后环,从而导致了从M0到M+或M-的跳跃,最终产生了所谓的簇发振荡.

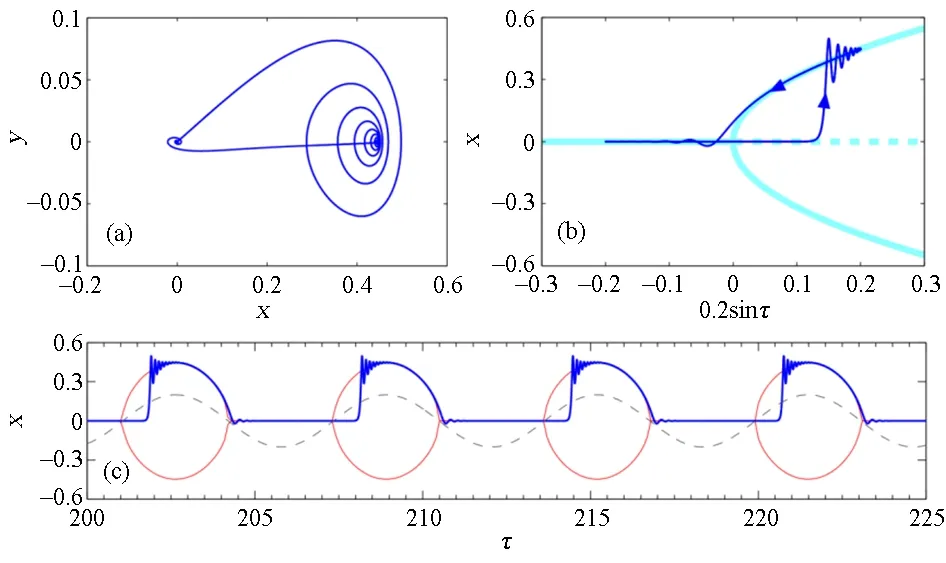
图3 当δ=0.1时,系统(2)中的簇发振荡,其中初值为(x0,y0,τ0)=(0.0001,0,0). (a) 簇发振荡的相图;(b)簇发的转换相图,其中叠加了图1所示的叉型分岔图;(c)簇发振荡的时间历程图,其中叠加了慢流形和慢变参数激励Fig.3 Bursting oscillations of system (2) for δ=0.1, where the initial conditions are (x0,y0,τ0)=(0.0001,0,0). (a) Phase portrait of bursting oscillations; (b) Transformed phase portrait of bursting oscillations, where the pitchfork bifurcation diagram shown in Fig. 1 is overlayed; (c) Time series of bursting oscillations, where the slow sub-manifolds and the slow parametric excitation are superimposed

由于叉型分岔的延迟现象在簇发振荡的产生中起着重要作用. 我们接下来分析在簇发振荡中观察到的这种延迟行为. 如前所述,延迟分岔的现象已经得到了广泛的研究[5-10, 17-19]. 根据文献[19]中描述的结果,叉型分岔的延迟时间可以定义如下.

设λ0,max(τ)是平衡点E0的特征值的最大实部.假设在τ=0处存在分岔,当τ1<τ<0时λ0,max(τ)<0,且τ0(τ1<τ0<0)是初始时间.设Ψ(τ0)为方程

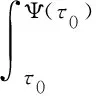
(7)

的最小正解. 这个最小正解Ψ(τ0)依赖于初始时间τ0.如果它存在,则称为分岔延迟时间. 如果不存在这样的时间,则分岔延迟时间是无限的.

将方程(7)应用于参数激励下的Duffing系统,并结合第2节中已给出的与平衡点E0有关的结果,我们可以通过解决方程

(8)

来计算延迟时间Ψ(τ0).其中τ*(τ*>τ0)是满足方程δ2+4γsinτ*=0的最小时间,即τ*是平衡点E0从稳定焦点变为稳定结点的最小时间点.由于方程(8)的解涉及椭圆积分,这是一个复杂的积分问题,我们将通过数值分析来解决它.如图4所示,延迟时间Ψ(τ0)可以通过使正面积和负面积相等来获得.因为Ψ(τ0)是相对于τ0的递减函数,显然

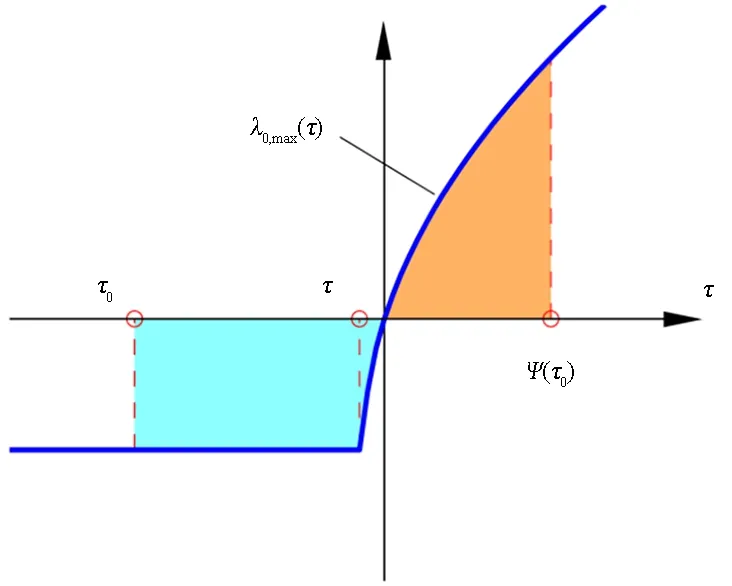
图4 函数曲线λ0,max(τ)的数值模拟.延迟时间Ψ(τ0)可以通过使蓝色和棕色区域相等来获得Fig.4 Numerical simulation of the function curve λ0,max(τ). The delay time Ψ(τ0) can be obtained by equating the blue and brown areas

较大的初始时间τ0意味着较少的延迟时间,例如参见图5.

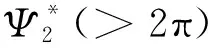
然而,正如我们在引言中提到的,与大多数其他论文研究的线性参数情况不同,这里研究的缓慢变化的参数激励是一个非线性周期函数. 因此,延迟行为将周期性地发生. 我们不妨把首次延迟行为的延迟时间称为“首次延迟时间”,用Ψ1(τ0)表示,即Ψ1(τ0)=Ψ(τ0).接下来的延迟行为的延迟时间可以用类似的方法来定义,例如Ψ2(τ0)表示第二次延迟行为的延迟时间,Ψ3(τ0)表示第三次延迟行为的延迟时间.

进一步的数值模拟表明,与首次延迟时间不同,对于固定的初始时间τ0,随后发生的延迟行为的延迟时间是不变的[即Ψn(τ0)是常数,n≥2].此外,正如我们上面所讨论的,不同的τ0意味着不同的延迟时间Ψ1(τ0).然而,如图6所示,对于与不同初始时间τ0相关的首次延迟行为之后的延迟现象,相关的延迟时间趋于一致.也就是说,初始时间τ0不影响随后的延迟行为,而只影响首次延迟行为. 因此,由等式(8)决定的延迟时间仅适用于首次延迟行为.

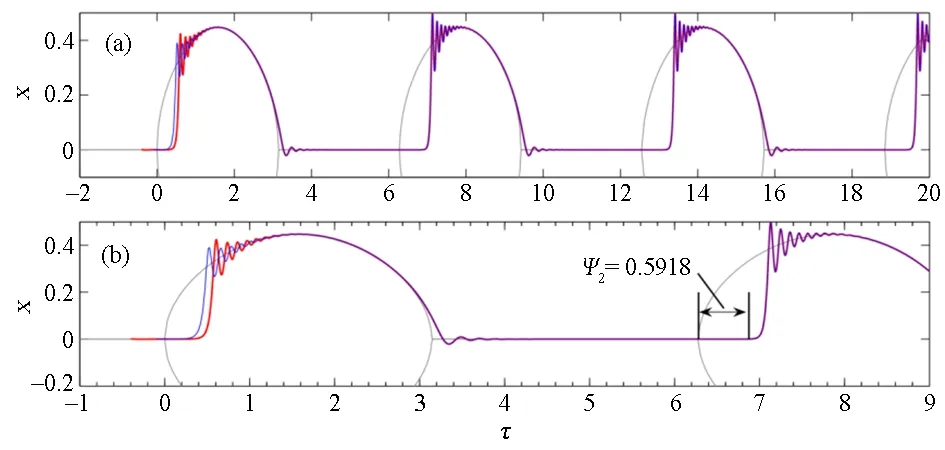
图6 不同初始条件下系统(2)中的簇发振荡,其中(b)是(a)的局部放大. 相关参数和初值和图5中的相同Fig.6 Bursting oscillations of the system (2) with different initial values, where (b) is the enlargement of (a). The associated parameters and initial values are the same as those of Fig. 5

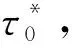
(9)

(10)

的最小正解. 显然,通过重置时间,第二次延迟行为的延迟时间Ψ2可以通过求解方程

(11)

的最小正解来等价地获得.以图6所示的簇发振荡为例,根据方程(11)计算出第二次延迟行为的延迟时间Ψ2=0.5918,这与数值模拟非常吻合.

类似地,通过重置时间,可以得出以下结论:首次延迟行为之后的所有延迟行为表现出与第二次延迟行为相同的延迟时间,即Ψn=Ψ2,n≥2,这与图3(c)和6(a)所示的数值结果一致. 因此,从长时间角度来看,所观察到的延迟行为的延迟时间不取决于初始时间τ0,而仅取决于系统参数.

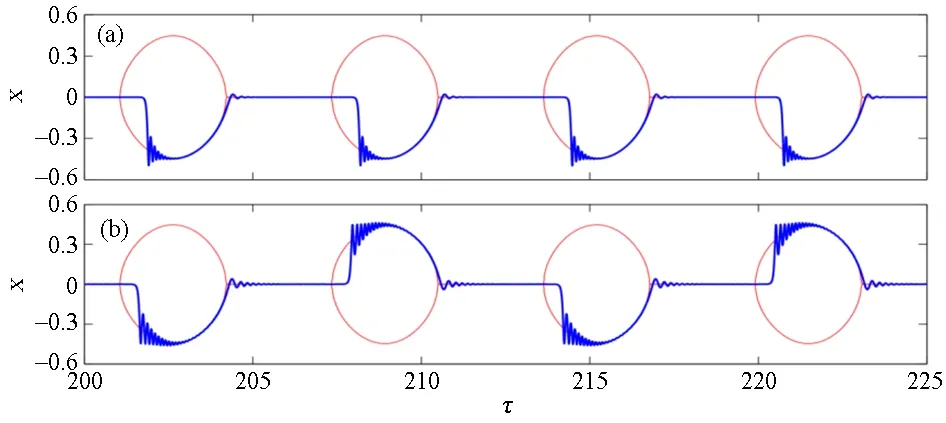
图7 系统(2)中的簇发振荡. (a) δ=0.1,初始值为(x0,y0,τ0)=(-0.0001,0,0);(b) δ=0.045

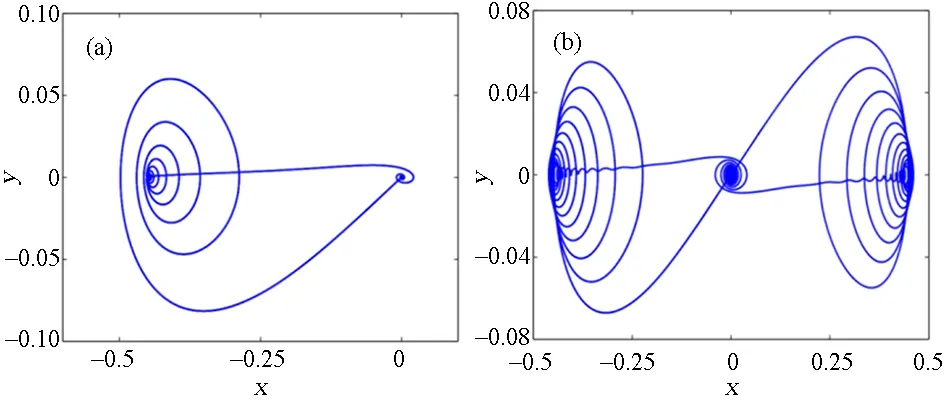
图8 图7所示的簇发振荡相对应的相图Fig.8 Phase diagrams corresponding to the bursting oscillations shown in Fig. 7

当0.2sinτ>0时,另一个有趣的现象是,存在两个稳定的慢流形M+和M-,这使得系统可以在它们之间进行选择.也就是说,在0.2sinτ增大并穿越0后系统会选择收敛到其中一个分支.至于选择哪一个分支,实际上取决于固定参数的初始值.由于系统(2)的向量场在坐标变换P: (x,y,τ)→(-x,-y,τ)下是不变的,因此很容易获得由慢流形M0和M-之间的跃迁形成的另一类簇发振荡[见图7(a)]. 这样两个共存的簇发振荡是相互对称的[见图3(a)和8(a)],随着参数δ的减少,它们可能整合成一个具有对称结构的簇发振荡. 当时,对称的簇发振荡如图8(b)所示.由于当系统从慢流形M0切换到慢流形M+和M-时,系统显示了叉型分岔延迟,因此产生了对称的簇发振荡(这可以通过上文给出的类似分析来理解).

图3、图6和图8(a)所示的簇发振荡是通过叉型分岔在两个慢流形M0和M+/M-之间切换形成的,所以根据文献[15]提出的簇发振荡分类方法,这种簇发振荡可以命名为“叉型分岔/叉型分岔滞后环”型簇发. 对于图8(b)所示的簇发振荡,考虑到其对称性,我们称其为“对称叉型分岔/叉型分岔滞后环”型簇发.

3 结论

当慢变参数激励周期性地通过叉型分岔点时,可以在参数激励下的Duffing系统中观察到簇发振荡. 这种振荡是由系统在稳定的慢流形之间的周期性切换产生的,这可以通过快子系统中涉及分岔的快慢过程来理解. 与簇发振荡有关的周期性切换,即从一个慢流形跳到另一个慢流形,是由叉型分岔的延迟行为导致的. 对于首次延迟行为,延迟时间由初始时间决定,而对于首次延迟行为之后的延迟现象,相关的延迟时间与初始时间无关. 因此,在簇发振荡中观察到的实际延迟时间一般不是由初始时间决定,而是由系统的参数条件决定的. 这种结果与控制参数是时间的慢变线性函数时的情况不同. 需要指出的是,这一结果同样适用于其他动力学系统中由慢变的参数激励引起的延迟行为.