基于解析法的高比例可再生能源系统惯量支撑储能配置
李志军,郭燕龙,苗庆玉
(1.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130;2.河北工业大学 电气工程学院,天津 300130)
0 引 言
随着化石能源的枯竭和人类生存环境的日益恶化,人们越来越多地将目光投向可再生能源。可再生能源大多通过电力电子接口与电网相连,通常惯量较低[1],这使得含高比例可再生能源的新型电力系统呈现低惯量的特征。较低的惯量水平使得系统的动态频率支撑能力被大幅削弱[2],当系统发生功率波动或机组停运等扰动时,初始频率变化率(rate of change of frequency,RoCoF)和最大频率偏差显著增大,严重时会触发低频减载(under frequency load shedding,UFLS)等保护机制,甚至引发大面积停电等重大事故[3],对电力系统的经济和安全运行造成严重威胁。
为应对新型电力系统惯量降低带来的问题,文献[4]提出了一种控制算法,根据系统的实时频率来调整可再生能源的输出,缓解因系统惯量下降带来的频率波动。文献[5-6]提出了虚拟惯量的概念,通过虚拟同步机(virtual synchronous generator,VSG)控制算法模拟同步机组的机电暂态特性,使得交直流变流器的输入输出特性接近于传统的同步发电机,有效提升了系统惯量。在可再生能源发电系统中,基于附加控制算法实现虚拟惯量的方法通常需要牺牲其发电经济效益来实现,且受制于有限的降载能量,所虚拟的惯量通常不能满足系统需要。储能系统(energy storage system,ESS)拥有启停灵活、响应快速的特点,近年来,已被广泛地用作VSG和其他虚拟惯量控制技术的能量源,通过合理的配置,即可为系统提供所需的惯量。由于成本等问题,需要根据系统的实时惯量值判断ESS是否需要投入,以及投入的功率值,这不仅涉及ESS配置问题,也是ESS惯量支撑后续控制等问题的基础。文章将对基于系统惯量支撑需求的ESS配置问题开展研究。
国内外学者对ESS配置问题已进行了大量研究,早期的ESS配置,大部分是基于仿真技术开展的。针对惯量支撑的ESS配置,文献[7]在MATLAB/Simulink中搭建了ESS-VSG模型,通过仿真法分析系统受到负荷阶跃扰动时对ESS的响应需求,对ESS进行了配置。文献[8]针对火电机组调频死区和响应速度问题,通过建模仿真方法,为辅助火电机组惯量响应的ESS做出了合理配置。文献[9]则通过对WSCC(western system coordinating council,WSCC)9节点测试系统进行负荷扰动下的潮流计算,实现了ESS的配置。文献[10]使用蒙特卡洛仿真对高光伏渗透率下的电力系统进行了ESS配置,提升了整个系统的频率支撑能力。上述基于系统惯量支撑的ESS配置均完全依赖于仿真计算技术,在系统较复杂时需要花费大量的时间,计算成本较高,也无法满足基于惯量在线配置ESS、优化ESS控制等实时应用的场景。
与仿真方法相比,解析法有着计算量小的显著优点,能够通过给出问题求解的显式表达式,更加直观地描述问题的解决思路,明确其物理意义[11]。另外,解析法可以通过给出近似解作为实时调度问题的基本框架[12],从而解决仿真法难以独立完成的问题。近年来,解析法在电磁场建模、潮流计算、可靠性评估等研究领域应用广泛。针对于ESS配置问题,文献[13-14]使用解析法对基于系统惯量支撑和一次调频的ESS做出了配置,并分析了不同可再生能源渗透率下ESS对于频率响应的贡献,但该文章使用各发电机组的加权惯量来表示系统的等效惯量,没有考虑传统机组的停运及可再生能源的波动等因素,无法客观地表达出高比例可再生能源系统中各种不确定性因素对系统惯量的影响。
针对上述问题,文章综合考虑了可再生能源及传统发电机组不确定性变化对系统惯量的影响,建立了传统机组的同步概率模型,以风电场为代表建立了可再生能源的同步概率模型,并以此为依据通过解析法求解系统期望惯量作为系统的实时惯量;以RoCoF指标为约束,根据摇摆方程求解系统的需求惯量,在系统惯量不足时配置ESS以保证系统频率稳定;最后,通过算例分析表明了所提方法能够满足系统惯量对ESS的需求,且极大地提升了计算效率,为ESS实时调配技术方案的实现提供了可能。
1 基于解析法的系统惯量建模
1.1 解析法系统惯量建模概述
基于惯量支撑的ESS配置以系统实时惯量为配置依据,为此,首先要对系统惯量进行建模。为客观反映机组运行时不确定因素的影响,此节对传统机组和可再生能源的同步概率分别进行建模,作为系统惯量求解的基础。
新型电力系统的系统惯量通常由可再生能源单元等效惯量和传统机组单元惯量构成,可再生能源出力具有随机性,同时也增加了传统机组投切的随机性,两者的随机特性使得系统惯量具有不确定性。另外,考虑到各发电单元只有在与系统并列同步运行的情况下才能为系统提供惯量,因此通过求解各发电单元的同步概率,即可客观的表达出不确定性影响因素下的系统惯量。
利用解析法求解系统惯量的示意图如图1所示。求解过程主要分为三个部分,首先对传统机组的同步概率进行求解,为此需要对系统停运容量、等效负荷进行建模,进而对传统机组期望发电量进行求解;其次,对可再生能源的同步概率进行求解,不同于传统机组,可再生能源同步概率的求解借助于其置信度来实现;最后,根据所有发电单元(包含传统机组和可再生能源)的同步概率及对应的惯量来对系统的实时惯量进行求解。
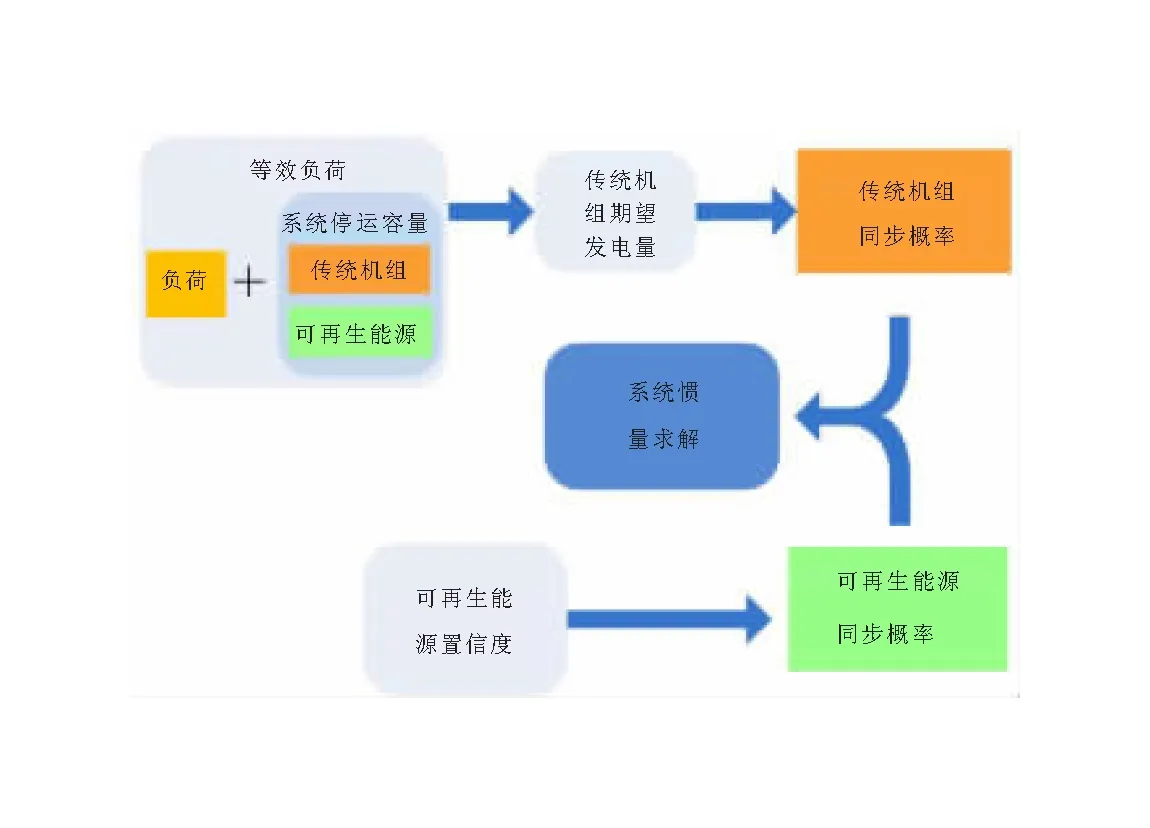
图1 解析法系统惯量求解示意图
1.2 传统机组同步概率模型
由图1可知,传统机组同步概率的求解包括系统等效负荷的建立、传统机组期望发电量的求解和传统机组同步概率的最终求解,此节将对整个过程依次进行建模和求解。
1.2.1 等效负荷模型
1)停运容量模型。
等效负荷由系统停运容量和负荷组成,此节首先对系统停运容量进行建模。由于传统机组期望发电量的求解需要借助于系统内所有发电单元的运行情况,所以系统停运容量是包含传统机组和可再生能源在内的全部发电单元的停运容量。
(a)停运容量概率分布。
文章使用系统的等效惯性时间常数来表征系统惯量的大小[15]。在不考虑发电单元停运问题时,系统的等效惯性时间常数Hr可用各发电单元惯量时间常数的容量加权和表示为:
(1)
式中Hi和Si分别为发电单元i的惯性时间常数和额定容量;Ssys为系统总装机容量。
由于各发电单元随机停运的影响,式(1)不再适用,为此需要对各发电单元的停运情况进行建模。一般情况下,当向原有系统中加入容量为Ca、停运概率为qa的二状态(即运行和停运两种状态)新机组时,所有发电单元的停运容量累积概率分布函数F+(C)可用式(2)所示的卷积过程[16]表示。
F+(C)=F(C)(1-qa)+F(C-Ca)qa
(2)
式中F(C)为加入新机组之前的停运容量概率分布函数。传统机组大多可用二状态模型表示。
可再生能源的停运容量模型一般为多状态形式,因此,若新投入可再生能源,F+(C)将表示为:
(3)
式中pi为总状态数为n的机组状态为i的概率;Ci为机组状态为i时,相对于其额定容量所缺失的容量。
通过将系统中所有传统机组的停运容量参数依次代入式(2),可再生能源的停运容量参数依次代入式(3),即可得到系统的停运容量概率分布。
(b)停运容量参数求解。
对于传统机组,式(2)中的qa、Ca可通过停运容量概率表(capacity outage probability table,COPT)或直接查找各机组的停运容量数据得到。对于可再生能源,式(3)中的pi、Ci并不能直接获得,为此,此节对以风电场为代表的可再生能源进行建模,并对多状态模型的pi和Ci值进行求解。
风电场的运行状态取决于风速及风电场中各风力机的停运情况,使用马尔科夫链可将风速近似等效为离散的有限状态[17],通过对大量时间序列下的风速样本进行处理,可得到各个风速状态的概率估计值。风速状态对应的概率可用式(4)表示。
(4)
式中pws,k表示风速状态为k时的概率;N为风速总的状态数;nkj为从状态k向状态j转变的状态个数。根据风速-功率曲线,可得到单个风力机在对应风速状态下的输出功率。
假设风速共有N个状态,风电场中共有m个风力机,则同一时刻风力机的停运个数g为0~m,风电场所有的状态数为N×(m+1),图2表示了风电场所有的状态及对应的停运容量。
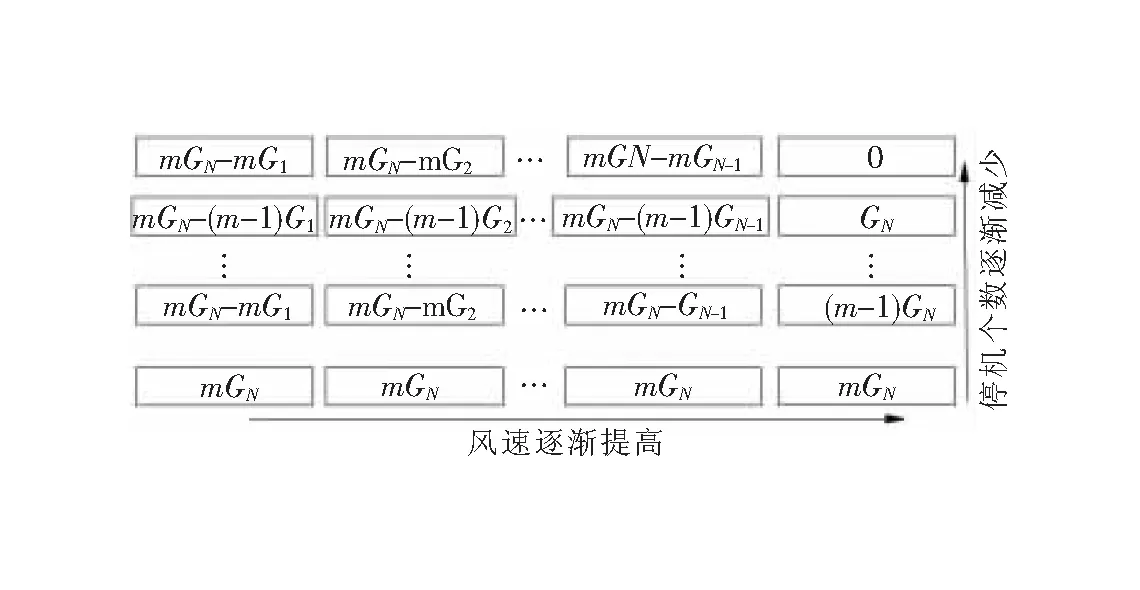
图2 风电场状态及对应的停运容量
当风速达到或超过临界值时,风力机达到其额定功率GN,若某时刻风速状态为k,且有g个风力机停运,则此时风电场的停运容量Ck,g为:
Ck,g=mGN-(m-g)Gk
(5)
式中Gk为风速状态为k时风力机的输出功率。则Ck,g所对应的停运容量概率pk,g为:
(6)
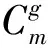
2)等效负荷概率分布。
电力系统稳定运行时,发电单元的停运会影响自身及其他发电单元的发电量[16]。为了对此影响结果进行合理表达,此节将负荷概率分布与(1)节中所建立的系统停运容量模型结合,即等效负荷模型,作为后文期望发电量求解的基础。
如式(7)所示,系统等效负荷Le为系统总负荷值L与发电单元总停运容量值C之和。
Le=L+C
(7)
通过将Le的各部分之间进行卷积,可得到系统等效负荷Le的概率分布函数F(Le)[15]。其中,L的概率分布可由负荷数据得到,文章通过对小时级负荷数据进行分析得到所研究时间范围内的负荷概率分布函数F(L)。当负荷为Li时,对应的概率分布函数FT(Li)可表示为[16]:
(8)
式中tL≥Li为负荷值大于Li的时间,ttotal为总时间。
将负荷概率分布函数F(L)作为式(2)中F(C)的初始概率分布,并使用1节中的方法对所有发电单元的停运容量依次进行卷积运算,最终可得到包含负荷与系统中所有发电单元停运容量的等效负荷概率分布函数Fn(Le)。
此节中的概率分布函数F(L)和Fn(Le)不同于一般意义上的累积概率分布,表示的是所研究数据中大于某个数值的部分所对应的概率,这样表达是为了更好地求解机组的期望发电量。
1.2.2 传统机组期望发电量求解
在得到等效负荷概率分布函数Fn(Le)之后,按照传统机组的优先级对Fn(Le)相继解卷积[15],以分别得到包含不同传统机组的等效负荷概率分布曲线。例如首先根据机组n的参数对Fn(Le)进行解卷积,如式(9)所示。
(9)
式中Fn-1(Le)为包含除机组n外的n-1个机组的等效负荷概率分布函数;qn为机组n的停运概率,对应式(2)中的qa。机组n的发电容量Sn和期望发电量En则可表示为:
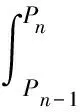
(10)
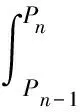
(11)
式中t为所研究的时间范围。
根据传统机组参数对Fn(Le)依次进行解卷积以得到包含n-1,n-2,…,1,0个传统机组,即分别移除1,2,…,n-1,n个机组的等效负荷概率分布函数。将所得的概率分布函数分别代入式(11)进行运算,最终可得到各传统机组的期望发电量。图3表示了上述解卷积过程以及Sn对应的区域。
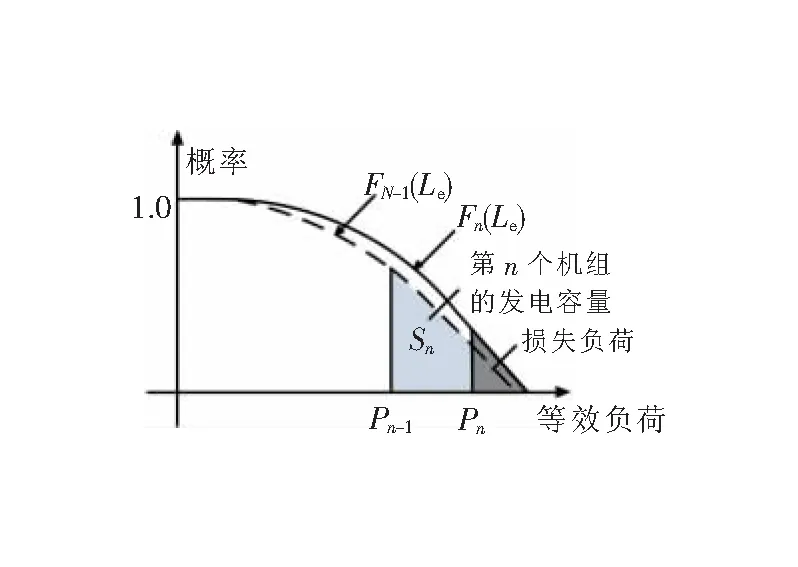
图3 第n个发电机组的发电量概率分布情况
1.2.3 传统机组同步概率求解
在得到传统机组的期望发电量后,即可对其同步概率进行求解。
在给定的时间段内,发电单元的期望发电量与其发电能力之比即为此发电单元的同步概率,如式(12)所示,将求得的各传统机组期望发电量依次代入式(12),可得到所有传统机组的同步概率。
(12)
式中psn为机组n在给定时间内的同步概率;Sn为机组n的发电容量。
1.3 可再生能源同步概率模型
对于可再生能源的同步概率模型,此节同样以风力发电作为典型代表开展相关研究。风电场通过电力电子接口并网,通常不能为系统提供惯量支撑,但是通过一定的控制技术可使其具有虚拟惯量。与传统机组不同,风电场的同步概率主要受其自身功率输出能力的影响,因此,利用风电场置信容量CV和容量置信度α可对其同步概率做出合理表征[18]。
风电场置信容量CV的定义是在维持系统可靠性不变的基础上,系统因发电单元的增加而相应可提升的负荷值。设Pw为此负荷值,Gw为风电场装机容量,则α为CV与Gw的比值,即:
CV=Pw
(13)
(14)
若所研究的时间范围为t,则负荷吸收的能量El为:
El=Pwt
(15)
同时,此能量值也是风电场的期望发电量Ew。风电场的同步概率psw可以表示为:
(16)
将式(13)代入式(16)并与式(14)比较可知,风电场的同步概率与α的值完全相等,即可用式(17)来求解风电场的同步概率。
(17)
1.4 系统实时惯量的解析模型
在任意时刻,系统惯量的可能值可表示为:
(18)
式中U为处于同步状态的发电单元集;Hn和Sn为发电单元的惯性时间常数和额定容量;h为此时刻的系统惯量值。
由于各发电单元同步状态的不确定性,导致h会随着各发电单元状态的变换而变化。为此,需要对各h值对应的概率进行求解,其表达式为:
(19)
式中P{Hr=h}为系统惯量等于h的概率;psn为发电单元n的同步概率,对应1.2和1.3节中的psn和psw;qsj=1-psj;D为处于非同步状态的发电单元集。
系统期望惯量E[Hr]即为h的期望,可表示为:
(20)
文章将E[Hr]作为系统的实时惯量,以体现系统中的不确定性因素对系统惯量的影响。
2 基于惯量支撑的解析法ESS配置
图4为利用解析法进行惯量支撑ESS配置的示意图,主要由传统机组、可再生能源、负荷及ESS构成。第1章已经建立了系统实时惯量模型,对应图4中的Hr,为完成解析法ESS配置,还需要得到系统需求惯量Hmin(即满足RoCoF约束下的系统惯量最小值),根据系统惯量的缺失值来对ESS的投入与否做出判断并计算ESS配置功率。

图4 考虑惯量支撑需求的解析法ESS配置示意图
2.1 系统需求惯量解析模型
当系统发生功率扰动ΔP后,初始时刻的频率的变化可用式(21)所示的摇摆方程表示[19]。
(21)

由此可得:
(22)
初始RoCoF根据不平衡事件突发后的0.5 s内的频率变化计算得到[20],其影响因素包括扰动大小、系统实时惯量、系统频率响应速度等。如果初始RoCoF过大,会导致系统频率下降超过允许值,触发UFLS。为此,需要将初始RoCoF限定在避免触发UFLS的允许范围内。文中取系统RoCoF的约束值为0.5 Hz/s[20],同时将此极端情况作为ESS配置的依据。
2.2 ESS投入功率
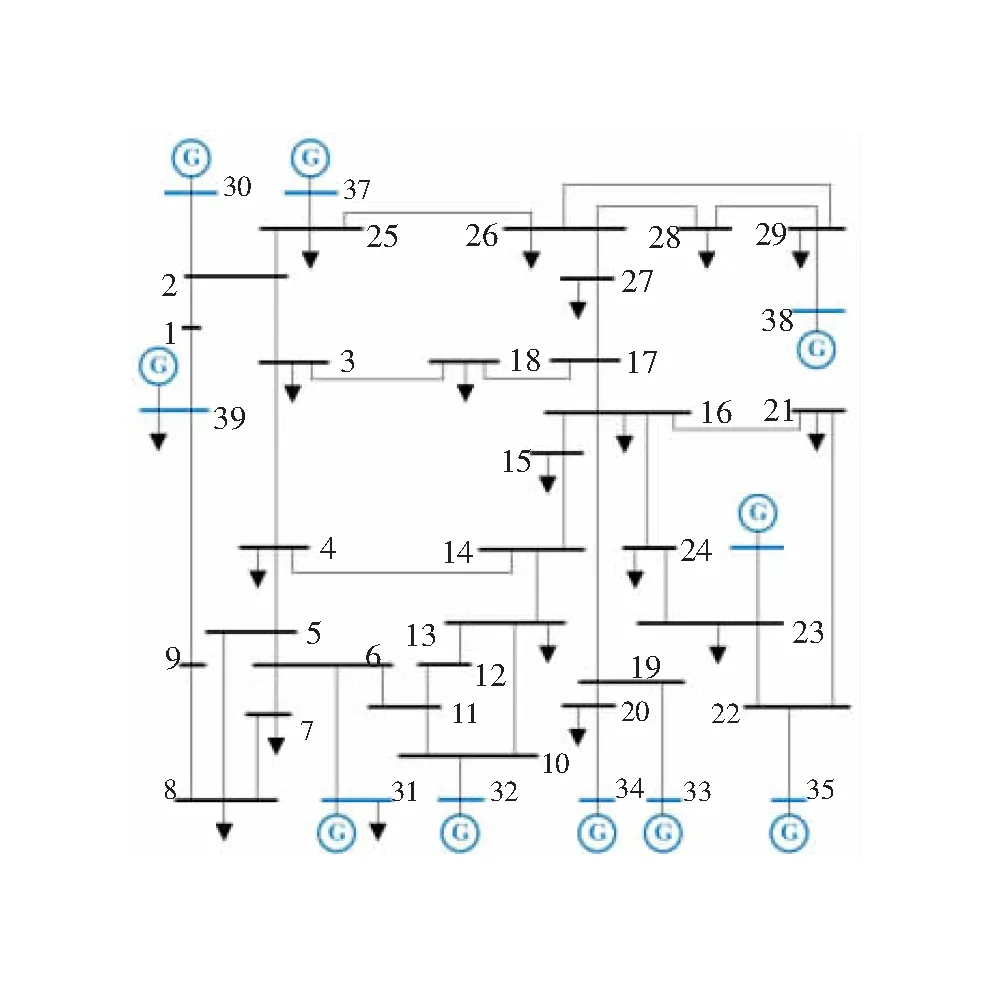
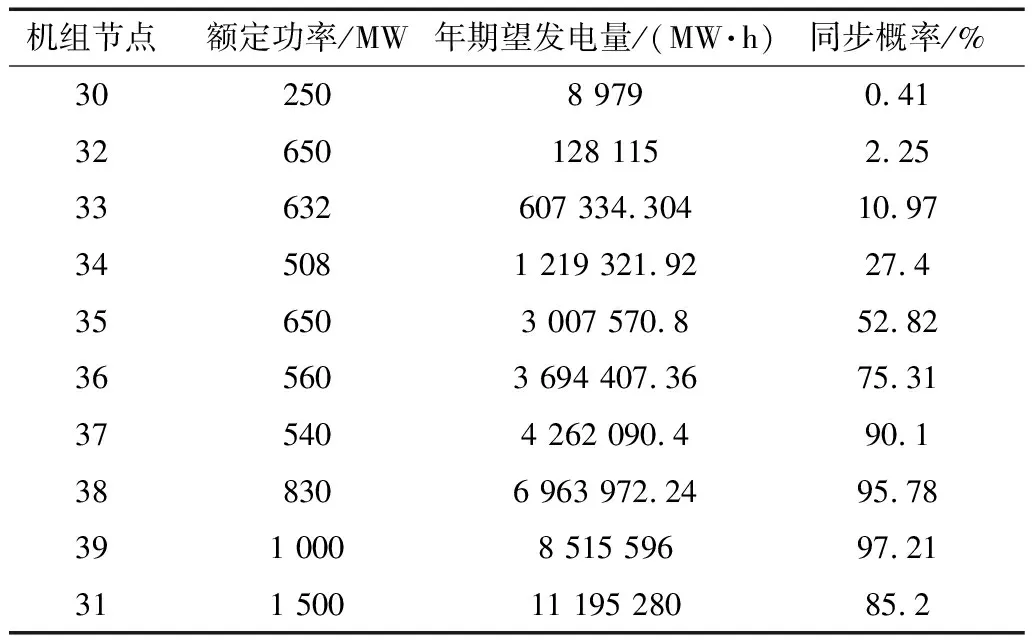
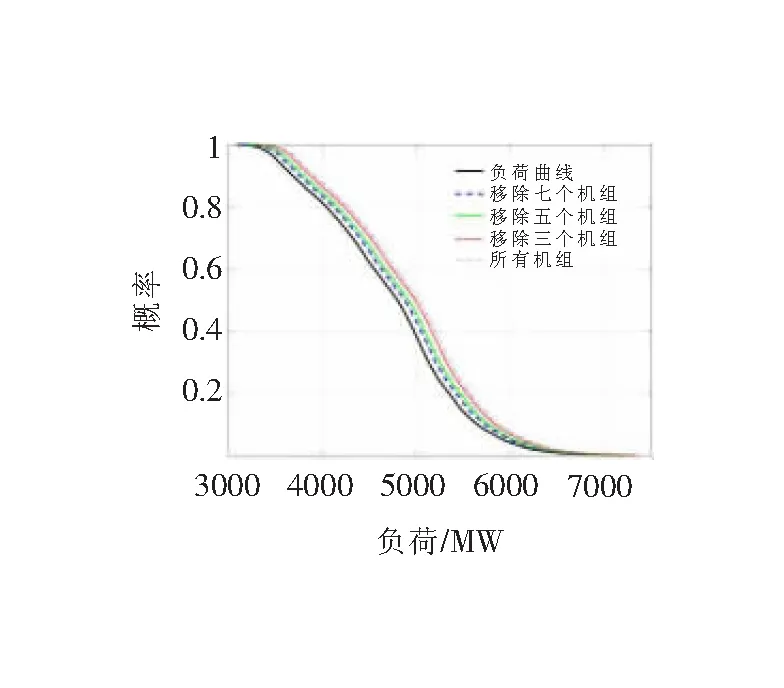
根据2.1节的模型可得到系统发生功率扰动时,RoCoF约束下的系统惯量需求Hmin,将1.4节中得到的系统期望惯量作为任意时刻t下的实时系统惯量Hsys(t)。若Hsys(t) HESS(t)=Hmin-Hsys(t) (23) 惯量为HESS的ESS在对频率变化做出惯量支撑时,其输出功率在虚拟同步机控制模式下同样可根据式(21)所示的摇摆方程进行求解,将式(21)中的Hmin使用HESS代替,解得ESS的投入功率PESS为: (24) 综上,基于解析法的系统惯量支撑需求ESS配置总流程如图5所示。 图5 基于解析法的惯量支撑ESS配置流程图 文章使用新英格兰IEEE 39节点系统的数据来验证所提方法的有效性。该系统包含39个节点、10个发电机组以及46条传输线路,其单线图如图6所示。根据场景的不同,将其中的部分发电机组替换为风电场来表示可再生能源的接入对系统惯量的影响。使用美国国家可再生能源实验室战略能源分析中心的风速数据来对1.3节中所描述的风电场进行建模[21]。风电场的容量置信度和同步概率取值为0.15[22]。引用我国北方某地区的年度小时级负荷数据,并根据算例系统中的峰值负荷来对负荷数据等比例缩放,以此建立负荷曲线。引用文献[23]中的发电机组停运容量及概率值来建立等效负荷概率分布,风电场的惯量值引用自文献[24]。 图6 IEEE 39节点系统单线图 使用四个具有不同风电渗透率的算例来验证文章所提ESS解析配置方法的有效性。在四个算例中,均设置0.1 p.u.的功率突变来求解系统的需求惯量。此外,文中所提方法适用于任意风电渗透率、负荷扰动限制下的ESS配置求解,在实际工程中可根据实际情况灵活选择以上参数。 1)算例1:所有发电机组均为原系统中的传统同步发电机组,所有机组的有功容量和为7 120 MW; 2)算例2:考虑大约12.5%的风电渗透率,使用容量为550 MW的风电场来替换原系统中250 MW和650 MW两个传统机组; 3)算例3:考虑大约28.5%的风电渗透率,使用容量为1 600 MW的风电场来替换原系统中250 MW、650 MW、632 MW和508 MW四个传统机组; 4)算例4:考虑大约38%的风电渗透率,使用容量为2 300 MW的风电场来替换原系统中250 MW、650 MW、632 MW、508 MW和650 MW五个传统机组。 算例1依据1.2.2节理论对包含所有发电机组的等效负荷概率分布曲线依次进行解卷积,最终得到了各机组依次被移除时等效负荷的变化情况。当所有发电机组均被移除时,等效负荷即为实际负荷,等效负荷概率分布曲线与负荷概率分布曲线重合。各等效负荷概率分布曲线如图7所示。将所得等效负荷概率分布曲线对应的函数依次代入式(11)和式(12),最终得到了各发电机组的期望发电量和同步概率,结果如表1所示。图8为系统惯量累积分布曲线,其中,惯量的取值范围为0—4.824 s,最终解得系统期望惯量E[Hr]为3.320 s。 表1 算例1各机组的期望发电量和同步概率 图7 算例1等效负荷概率分布曲线 图8 算例1系统惯量累积分布曲线 由于风电场的渗透,算例2~算例4的系统惯量的取值范围分别为0—4.399 s、0—3.703 s和0—3.269 s,系统期望惯量分别为3.236 s、3.017 s和2.762 s。 为了验证文章所提解析方法的有效性,使用了文献[10]中的蒙特卡洛仿真方法来对系统惯量进行求解,最终求得的四个算例中的系统惯量分别为3.399 s、3.313 s、3.089 s、和2.813 s,与解析法的求解结果误差均在3%以内。 根据第2章所提方法来计算ESS需求惯量和投入功率值,其结果如表2所示。结果表明,在规定的RoCoF约束下,对于算例1和算例2,系统本身具有足够的惯量。随着风电渗透率的提高,在算例3和算例4中,需要调度并投入相应的ESS来为系统提供更多的虚拟惯量。与之相对应,表3给出了蒙特卡洛仿真法的ESS配置结果,所提解析法与仿真法所得结果中,ESS均在算例1和算例2中不投入使用,在算例3和算例4中投入使用,且ESS配置误差均在5%以内。 表2 解析法的ESS配置结果 表3 仿真法的ESS配置结果 文中算例中所使用的计算机处理器为i5-6600,软件为MATLAB2018a。整个ESS配置过程,解析法耗时约0.78 s,仿真法耗时数十分钟,表明在考虑随机特性的惯量求解和ESS配置实时性应用场景中,解析法具有良好的实时匹配能力。 通过以上的分析以及与模拟仿真结果的对比,表明了所提ESS解析配置方法能够在保证计算结果准确性的基础上较大地提高计算速度和效能。 3.4.1 ESS配置的动态频率支撑效果 为了验证所提ESS配置方法的动态频率支撑效果,分别将算例1~算例4的ESS配置结果代入IEEE 39节点系统中,分析当系统遭受0.1 p.u.的负荷波动的情况下的初始RoCoF的变化情况并与无ESS配置下的系统进行对比,其结果如表4所示。由表4中数据可知,算例3和算例4在ESS配置前后,其初始RoCoF均由不合格转变为合格状态,且配置ESS后的初始RoCoF接近于约束值,既保证了支撑效果,也避免了ESS的过度配置。 表4 ESS配置前后RoCoF对比 此外,算例1和算例2在无ESS配置的情况下即可满足RoCoF的要求,这也验证了所提方法对于系统需求惯量计算的准确性。 3.4.2 ESS的实时在线配置效果 为了验证所提方法的实时在线配置效果,在2 s、15 s和30 s时分别将系统的参数由算例1更改为算例2~算例4所对应的参数,并于1 s后产生0.1 p.u.的功率扰动,分析其初始RoCoF的变化情况,并与离线配置的结果相比较,其结果如表5所示。 表5 ESS实时在线配置效果 由数据可知,在系统状态为算例1和算例2对应参数时,由于系统本身惯量能够满足标准要求,故离线配置和在线配置中ESS均未投入使用。当系统状态变为算例3和算例4对应参数时,由于离线配置计算时间较长,无法根据系统最新状态对ESS配置做出改变,故ESS未能及时投入,初始RoCoF超过了约束值。而所提方法能够较好地感知系统参数的变化,并据此实时调整ESS配置,使得初始RoCoF仍满足系统要求。 以上分析表明了所提方法能够实现ESS实时在线配置的可行性和有效性。 高比例可再生能源电力系统拓扑复杂多变,使得系统频率特性具有强烈的不确定性特点,传统的基于仿真技术的ESS配置方法通常计算成本高、效率低,无法满足新型电力系统多变的实时在线配置需求,现有的解析法配置技术无法客观反应出新型电力系统中各种不确定性因素对系统惯量的影响,使得ESS配置不够客观、准确。针对这一问题,文章提出了一种新型的基于解析法的ESS配置方法,综合考虑了可再生能源和传统机组的不确定性问题,为用于惯量支撑的ESS提出了一种新型解析配置方法,经过理论分析和算例验证,主要工作总结和结论如下: 1)使用概率统计的方法建立了系统惯量解析模型,设计实现了基于解析法的ESS配置并客观反映了系统不确定性的影响; 2)与传统蒙特卡洛仿真配置方法对比,该解析配置方法不仅能满足ESS的准确配置,计算效能也得到了大幅提升; 3)基于所提方法的高效能,使得利用其实现ESS实时在线配置成为可能,可满足新型电力系统实时调控的需求。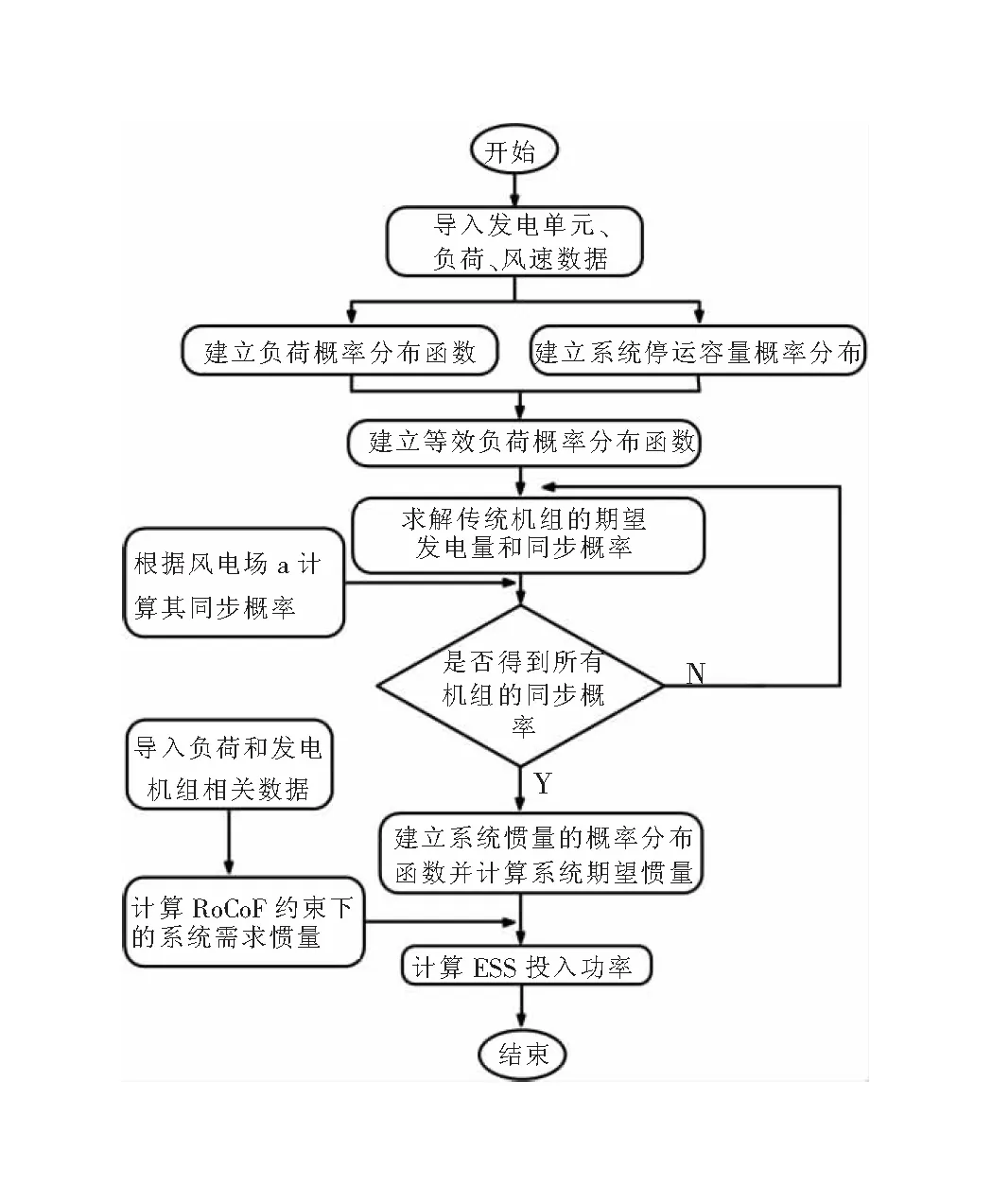
3 算例分析
3.1 算例介绍
3.2 传统机组同步概率和系统期望惯量

3.3 ESS配置结果


3.4 ESS配置效果


4 结束语

