面向遥感图像旋转目标检测的双向衰减损失方法研究

张 正 马渝博柳长安 田 青

(北方工业大学信息学院 北京 100144)

1 引言

遥感图像中地物目标分布情况能够反映人群、军队等的整体运动趋势和行为逻辑，准确而高效地在遥感图像中检测并识别出所需的目标，对于基层建设、交通规划、军事行动等具有重要的现实意义和实际应用价值。

针对遥感图像中的目标检测问题，传统的方法通常基于手工设计的特征[1–3]，但是其特征表达能力弱、鲁棒性差、适应范围小，难以应用在复杂多变的环境中，远不能满足实际应用需求。随着深度学习的发展，神经网络的应用推动了目标检测领域的发展[4,5]，出现了RCNN系列[6–8]为代表的双阶段目标检测算法，以及YOLO系列[9–11]、SSD系列[12]和RetinaNet[13]为代表的单阶段目标检测算法。但是在遥感图像中，由于车辆、船舶、飞机等目标具有尺寸小、方向任意且长宽比较大的特点，普通视角下的水平目标检测算法尚不能取得良好的效果，因此又相继出现了如RoI T ransformer[14]、R3Det[15]等旋转检测算法，在水平目标检测方法的基础上提出了对旋转角度的预测。角度值的加入极大减少了检测框中背景冗余信息的干扰，有利于约束网络的训练方向和减少网络的收敛时间，但是在旋转检测中预测框与真实值间的损失计算上却产生了新的挑战。

由于旋转目标检测相比水平目标检测增加了角度信息，在大多数旋转目标检测算法中普遍存在由角度值引起的损失值变化与实际情况不一致的问题，主要原因有两点：由于角度定义区间的边界性，检测框的回归路径无法越过边界，只能从相反方向通过更远的路径进行回归，导致计算得到的损失远大于实际情况；边的互换性，即检测框在旋转90°并交换长短边后与其原本在直观上是等效的，但表达方式的不同会使网络产生额外的损失。针对上述问题，以分类思想进行角度预测的DCL[16]方法解决了角度的边界性问题，但是仍未解决边的互换性问题。部分学者展开了基于交并比(Intersectionover-Union,IoU)的损失函数计算方法的研究，试图规避角度值所引发的相关问题。IoU是最能直观反映预测误差的度量手段，但是旋转框之间的IoU(下文简称为偏斜IoU)难以计算和用于反向传播，所以找到近似的偏斜IoU计算方法并将其作为损失函数的计算依据，成为目前旋转检测中最具前景的研究方向。相关的工作如PIoU通过统计像素[17]计算交并比，GWD[18],KLD[19]将旋转框转化为高斯分布后进行距离度量计算。此类方法有效解决了角度边界性和边的互换性等与角度值相关的问题，但均无法与偏斜IoU保持良好的一致性，在遥感任务中未能取得优秀的检测效果。

Yang等人[20]在GWD,KLD的基础上进行改进，其最新的成果KFIoU(Kalman-Filter-IoU)损失通过高斯相乘的计算方法，解决了角度边界性和边的互换性问题的同时，实现了损失与偏斜IoU的趋势级一致，且具有完全可微性和处理非重叠情况的能力，性能表现优秀。但是KFIoU损失依旧存在损失值与实际变化趋势不一致的问题，这主要是由于其采用的中心点损失无法反映预测值的偏移方向，而不同的偏移方向实际上会带来不同的偏斜IoU表现。

本文尝试进一步解决KFIoU损失函数的损失值与偏斜IoU实际变化不一致的问题。受其启发，本文提出了一种新的双向衰减损失函数(Bidirectional A ttenuated IoU,BAIoU)。具体而言，首先本文依旧基于高斯乘积进行偏斜IoU的近似计算。然后，本文没有使用中心点损失，而是通过为高斯乘积引入一个双向衰减系数来反映预测值与真实值间的位置偏差，因为双向衰减系数能够使损失携带位置偏差的方向信息。新的损失可以解决KFIoU损失的不一致问题，使网络获得更优的回归路径。

本文的主要工作包含以下两点：(1)在第2节提出一种新的基于旋转目标检测的偏斜IoU近似损失——双向衰减损失，继承KFIoU损失不受角度边界性和边的互换性影响的优点，创新性地提出使用衰减系数代替中心点损失，所提损失函数在趋势上更加贴近于偏斜IoU的客观变化规律。(2)在第3节设计多组实验比较双向衰减损失和KFIoU损失的精度表现，证明引入衰减系数的方法进一步完善了与偏斜IoU的趋势级一致性。

2 双向衰减损失

2.1 KFIoU损失

KFIoU损失继承了GWD使用高斯分布的思想，并受卡尔曼滤波的启发通过高斯分布乘积模拟重叠区域，计算过程如图1。KFIoU损失包含两个部分：

图1 KFIoU损失的偏斜IoU逼近过程

(1)首先用GWD中的方法将真实值和预测值两个旋转框B(w,y,h,w,θ)转 化为高斯分布G(µ,Σ)，通过所得两个分布的中心点距离计算中心点损失LC，用于缩小两个高斯分布中心点之间的距离；

(2)通过卡尔曼滤波计算得到重叠区域的高斯分布，并将其转化为面积与重叠区域近似的旋转矩形框vB，通过所得重叠区域矩形框、预测值和真实值计算KF损失，即模拟偏斜IoU的计算方式。

最后将中心点损失和KF损失相加即为最终损失。

其中，f(·)表 示关于KFIoU的函数，如-ln(KFIoU+ε)、1-KFIoU或e1-KFIoU-1。vB为3个旋转矩形框，如图1(d)所示。

然而本文发现，KFIoU损失存在损失与实际情况不一致的问题：图2展示了两个形状相同且长宽比为2:1的预测值bbox1,bbox2，在具有相同偏移距离、不同偏移方向时的偏斜IoU表现，在图中可以明显地看到两者的实际偏斜IoU存在很大差距。若通过KFIoU计算，此时中心点损失L c(Cgt,C1)=L c(Cgt,C2)，而Lkf只与旋转角度有关，最终导致两个预测框的损失是相同的。以此类推当预测框中心点落在一个半径相同的圆上任一点时，所得KFIoU损失值相同，即KFIoU损失无法反映偏斜IoU由中心点位置偏差的方向所引起的偏斜IoU变化，存在损失与实际情况不一致的问题。这种不一致问题在长宽比普遍较大的遥感目标上更加明显，因为其根本原因是目标的长宽差异。

图2 两种偏移情况下的偏斜IoU表现

2.2 双向衰减损失

针对KFIoU存在的问题，本文在其基础上提出了一个新的损失函数：双向衰减损失(Bidirection A ttenuated IoU,BAIoU)。图3是双向衰减损失对偏斜IoU的逼近过程，其沿用了KFIoU损失的高斯相乘方法以有效回避角度预测产生的相关问题。双向衰减损失同样通过式(3)计算的KFIoU结果来反映预测值的角度误差，而偏移误差的反映方式不再采用中心点损失，而是通过对所得近似值依据偏移方向与偏移距离进行相应衰减的方式，反映出预测值的不同偏移情况。下文将对衰减方式展开讨论。

图3 双向衰减损失的偏斜IoU逼近过程

假设真实值和预测值为一个长4、宽2且旋转角度相同的矩形框，真实值中心点为坐标原点，x轴、y轴分别沿其短边和长边方向，预测值相对真实值的偏移量作为x,y坐标的值，后文(图4—图7、图10)也将在此情景讨论损失函数对中心点偏移误差的反映能力。从图4可以看出偏斜IoU的递减趋势，其随偏移误差的增加在真实值长边方向相对缓慢减小，在短边方向则相对快速减小，且两个方向的斜率比与矩形框的长宽比相同。所以本文方法将式(3)中的KFIoU结果乘以一个衰减系数α使得损失的变化贴近偏斜IoU的变化规律。衰减系数分别依据中心点偏移量在真实值的长、宽两个方向的投影长度(如图5)，将矩形框面积衰减至与实际偏斜IoU近似的大小。通过这种方法，双向衰减损失可以同时反映预测值偏移误差和角度误差带来的偏斜IoU变化。

图4 偏斜IoU关于预测值偏移量的变化图像

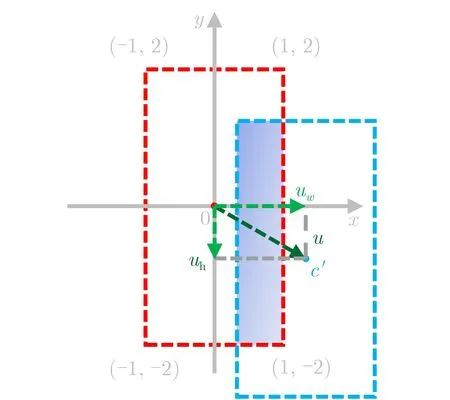
图5 中心点偏移向量在真实值长边(y轴)和短边(x轴)方向的投影

新的损失函数表达式为

其中：f(·)表 示关于BAIoU的函数，如- ln(BAIoU+ε)、1-BAIoU 或e1-BAIoU-1。‖u h‖和‖u w‖分别为真实值中心点到预测框中心点连线向量u在真实值长边和短边两个方向的投影长度，作为衰减系数中的自变量，如图5所示。‖u h‖和‖u w‖的值可分别通过投影公式得到，超参数λ取值为1.75(λ取值将在实验部分解释)。

遥感目标具有尺寸分布跨度大、长宽比不一的特点。为了更好地反映具体目标的不同尺寸信息，本文引入了缩放因子S h和Sw。缩放因子的作用是针对具体目标的长、宽设计损失在两个方向的相对衰减幅度，其值分别为预测框在长边和短边两个方向的最远衰减距离，即偏斜IoU衰减为0时的中心点偏移距离，如图6所示。具体计算过程如下：

图6 最远衰减距离

其中，wgt和hgt为真实值的宽和高，wpre和hpre为预测框的宽和高，ugt和upre分别为真实值和预测框的长边所对应的向量。ugt·upre为向量的内积，同时对内积取绝对值以保证计算过程夹角取值小于9 0°。

双向衰减损失相比于KFIoU及大部分常规损失函数，有如下5个特点：(1)由于双向衰减损失依旧和KFIoU损失一样基于高斯分布，通过卡尔曼滤波计算近似重叠区域，在计算过程中不受角度定义区间边界性和边的互换性影响，并且其改进部分(衰减系数)的计算也不需要引入额外算子，同KFIoU损失一样易于实现；(2)对于预测值与真实值的非重叠情况，由于衰减系数为指数函数，相比于KFIoU损失中的中心点损失，能够在贴合偏斜IoU变化趋势的基础上保证即使预测框偏移量巨大，损失值也始终不为零，所以双向衰减损失具有更优的非重叠情况计算能力；(3)双向衰减损失在真实值长、宽两个方向拥有不同的衰减率和衰减距离，因此网络能够分辨预测值的相对偏移方向，从而优化回归路径，获得更快的收敛速度，这是KFIoU所不具备的；(4)衰减系数的衰减率和衰减距离由具体目标的长、宽决定，针对不同长宽比和尺寸的目标精细化回归，能够满足遥感背景下目标长宽比差别大、尺寸跨度大的特点；(5)相较于KFIoU损失通过中心点损失拉近两个分布后进行高斯相乘的计算过程，双向衰减损失根据偏移量直接减小高斯相乘结果的计算过程也更加贴近偏斜IoU的实际变化规律，拥有更好的自然性。

为了直观地观察衰减系数和偏斜IoU的变化趋势，本文在图4所设场景下统计了衰减系数随偏移量的变化图像，从图7可以直观地看到衰减系数与图4中实际偏斜IoU的整体变化趋势高度一致。

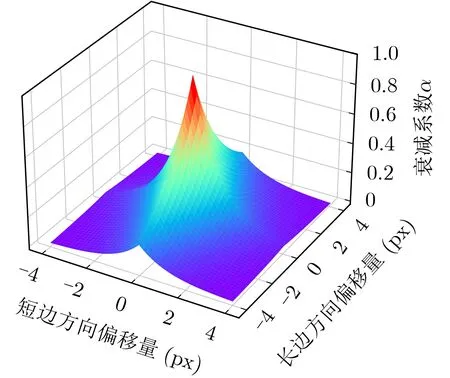
图7 衰减系数关于偏移量的变化图像

3 实验与分析

3.1 数据集和实验环境

本文实验选用DOTAv1.0目标检测数据集[21]，在其中选择了具有较高应用价值和代表性的5类交通工具目标(飞机、小型汽车、大型汽车、船、直升机)进行实验，他们综合覆盖了方形目标(飞机)、大长宽比目标(大型汽车)、密集排列目标(船、汽车)和数据集中尺寸最小的目标(小型汽车)等遥感目标检测的难点、重点目标。实验中将图像按照600像素×600像素分割，重叠区域为150像素，并缩放到800像素×800像素，这与主流的裁剪方法一致。数据增强采用随机旋转和翻转。图8展示了数据集中目标长宽比的分布情况，其中目标的长宽比主要集中在2:1附近，且为表达清晰，本文主要以长宽比2:1的目标举例说明。

本文采用的评价指标为平均准确率(Average Precision,AP)的计算方式Interplolated AP[22]。硬件配置为Intel(R)Xeon(R)Silver 4210R处理器，4个NV ID IA 2080T i显卡，软件环境为Ubun tu 18.04。

3.2 基于双向衰减损失的目标检测

本文相关实验选用RetinaNet作为基础目标检测网络，骨干网络为ResNet101，使用Adam优化器。使用了双向衰减损失的RetinaNet旋转检测网络结构如图9所示。网络最后会输出5个特征层P1～P5。其中P1～P3是经过特征融合操作输出的，P4～P5是在ResNet的最后一层特征层上通过额外卷积操作获得的。旋转检测模型中预测器的回归部分加入了角度预测，其损失函数选用本文的双向衰减损失。

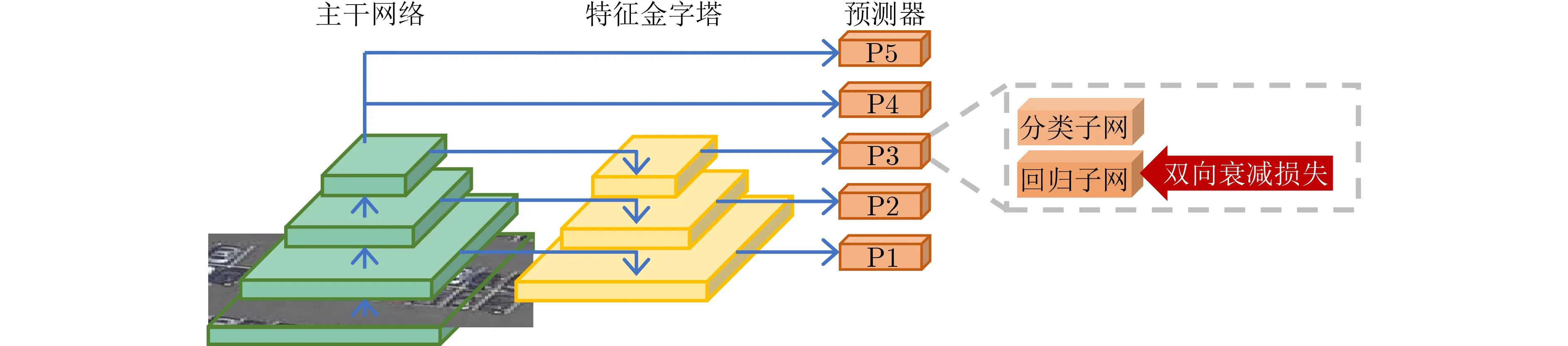
图9 结合双向衰减损失的RetinaNet网络结构

3.3 损失偏差量和超参数

在2.2节中衰减系数所包含的超参数λ，用于进一步修正损失的整体衰减速率以贴近偏斜IoU的实际变化趋势。为了研究衰减系数的整体变化趋势是否符合偏斜IoU，本文对两者的斜率和差值进行统计比较。在图4和图7中两者的变化曲面上的斜率偏差计算较为困难，且任意一点的取值均与x轴、y轴上的值直接相关(比例乘积关系)，故坐标轴截面的曲线可以反映整体曲面的趋势差异。图10(a)展示了坐标轴正半轴截面上衰减系数和归一化偏斜IoU的图像(设真实值和预测值的尺寸均为4×2且旋转角度相同，真实值的中心点设为原点，x、y分别为短边和长边方向的偏移量，x,y ∈[0,10])，其中实线代表衰减系数，虚线代表偏斜IoU，蓝色代表y=0时函数关于x的变化，黄色代表x=0时函数关于y的变化。

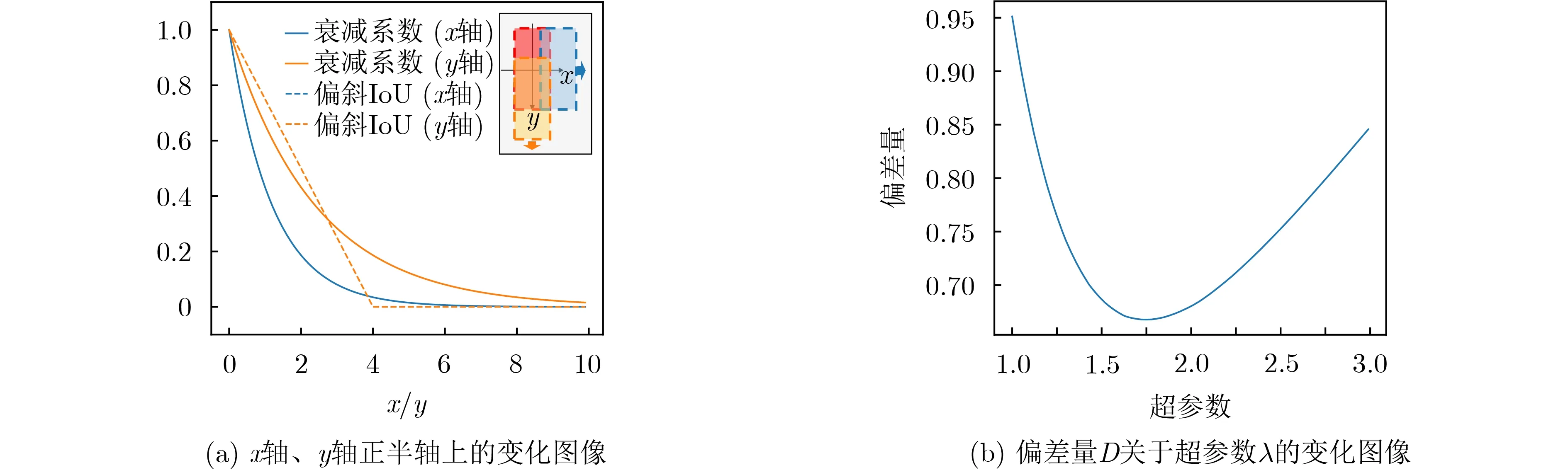
图10 衰减系数与归一化偏斜IoU的差异比较

本文设定了一个偏差量D：

其中，(x,y)为预测值相对真实值沿短边偏移了x、沿长边偏移了y，α为此时的衰减系数取值，skew IoU为此时的偏斜IoU的值，n orm表示已进行归一化，k(x,y)为此时衰减系数或偏斜IoU变化曲线的斜率。

偏差量D用于近似衡量双向衰减损失与实际偏斜IoU之间的偏差量。其由两部分组成：差值和斜率差，其中斜率差的权重为差值的5倍，因为我们更加注重两者的趋势一致性。图10(b)是D关于超参数λ的变化曲线，其中各项条件与图4相同，计算范围取x,y ∈[0,10]，并在其中均匀取100个点计算，此区间可以代表双向衰减损失和实际偏斜IoU的整体变化趋势。图中数据显示偏差量在λ=1.75时取得最小值。此外，本文在RetinaNet网络模型上进行了测试，测试结果如表1所示。表中实验数据的规律符合推理结论，进一步验证了偏差量D及λ取值的合理性。

表1 不同λ 取值对RetinaNet网络检测性能的影响

3.4 消融实验

为了验证双向衰减损失的有效性，本文基于RetinaNet网络结构，测试了几种不同形式的损失计算方式在DOTAv1.0数据集上的检测精度表现，如表2。与KFIoU在指数函数取得最高的性能不同，由于双向衰减损失能够使网络更快回归高IoU的预测框，其在对数函数上相比KFIoU提升了可观的1.66%。最终，基于指数函数的双向衰减损失获得了最高71.24%的检测精度。

表3通过AP精度比较了KFIoU损失和双向衰减损失的几种不同精度表现。对于DOTAv1.0数据集，双向衰减损失在各指标均取得优势。同时值得注意的是，因为双向衰减损失更好的偏斜IoU模拟过程，在AP75相比KFIoU取得了3.42%的明显优势。最终双向衰减损失在AP 50:95上取得了2.61%的提升。

表3 基于不同损失函数的目标检测精度比较

此外，本文使用COCO数据集[23]，基于RetinaNet网络结构在水平检测任务上也对双向衰减损失进行了验证，如表4。双向衰减损失与GIoU等常见损失函数基本持平，因为在水平条件下，高斯分布的计算方法会退化得与常见水平回归损失相似，这一点符合文献[20]中的结论。

表4 双向衰减损失与经典水平损失函数的检测精度比较

3.5 本文方法与现有方法的对比

表5在DOTA v1.0的5类典型目标上比较了几种最新的主流损失函数。由于不同的方法使用不同的最佳训练策略和技巧，无法进行绝对公平的比较。通过我们所作实验，在RetinaNet模型中，SmoothL1损失作为一种经典的非偏斜IoU损失取得了56.14%的m AP；首个使用高斯分布的高性能损失函数GW D使用高斯分布间的距离度量作为依据，其取得了68.39%的m AP；目前最先进的损失方法KFIoU更具创新性地对高斯分布进行高斯相乘来模拟偏斜IoU，相比GWD取得了1.91%的提升；本文的双向衰减损失则通过使损失反映偏移误差的变化，相比KFIoU进一步提升了0.94%的m AP。值得注意的是，其中双向衰减损失在大型汽车目标上相比KFIoU获得了2.6%的较大提升，因为其对回归路径的优化使得在较大长宽比的目标上拥有一定优势。在R3Det模型中，非偏斜IoU方法的DCL分类思想代替角度回归，取得了75.15%的m AP；KLD与GWD相似，优化了中心点偏移问题和尺度不变性问题，达到了78.32%的m AP；KFIoU进一步提升了1.22%达到了79.54%的检测精度；本文的双向衰减损失相比KFIoU再次提升了0.6%，且对每种目标均取得了最高的检测精度。最终就整体性能而言，本文方法在此数据集上取得了最好的检测效果，约为71.24%(RetinaNet)和80.14%(R3Det)。

表5 不同损失函数在DOTAv1.0中5类典型目标的检测结果对比(%)

3.6 检测结果展示

图11展示了DOTAv1.0测试集上的部分结果，本文方法能够准确地定位目标的位置，精确地回归目标的形状与方向，各类目标均能取得较为优秀的检测效果。

4 结论

本文在KFIoU损失的基础上提出了一种与偏斜IoU更具一致性的损失函数：双向衰减损失。双向衰减损失通过在KFIoU损失中添加一个衰减系数，使其能够通过两种衰减的叠加反映预测框的偏移误差信息。同时双向衰减损失也继承了KFIoU损失的诸多优点，如易于实现、不受角度预测问题的影响、能够计算非重叠情况以及与偏斜IoU趋势上的高度一致性等。实验证明，相比KFIoU损失，双向衰减损失在不同的基底函数和IoU阈值上，其检测精度均取得了不同程度的提升。