小半径曲线段盾构隧道掘进过程中地表变形规律

陈晨 朱新健 王永 焦凯 赵向辉

1.中国水利水电第三工程局有限公司， 西安 710024； 2.长安大学 公路学院， 西安 710064

在城市地下轨道交通建设中，曲线段盾构隧道工程案例越来越多。与直线段相比，小半径曲线段盾构隧道地表变形规律更复杂，施工控制要求更高。

许多学者对小半径曲线段盾构隧道的地表变形规律进行了研究。理论分析方面，文献［1-2］基于镜像法及Mindlin解，推导了曲线段盾构隧道开挖引发的地表沉降计算公式。文献［3-4］求解了考虑盾构铰接作用时小半径曲线段盾构隧道开挖诱发的地层沉降计算公式。文献［5］对软土地区盾构施工过程中曲线段超挖量进行了理论计算，给出了曲线段超挖引起地表沉降的防控措施。数值模拟方面，文献［6-7］研究了小半径曲线段盾构施工时周围土体变形规律，并分析了半径对地层变形规律的影响。文献［8-9］针对不同千斤顶推力下开挖面受力状态的差异，给出曲线段盾尾间隙的计算方法，并分析了盾尾间隙对地表位移的影响。文献［10］运用数值模拟和现场监测相结合的方法，对南通一小半径曲线段盾构隧道施工超挖和转弯引起的地层变形进行了研究。文献［11］建立了考虑仿形刀超挖的精细化模型，研究了曲线段盾构隧道施工引起的地层变形特征及隧道埋深对地层变形的影响。

既有文献对小半径曲线段盾构隧道施工引起的地表变形规律研究较多，但考虑千斤顶分区推力和曲线内侧超挖的数值模拟较少。本文以西安地铁2号线正北区间（正阳大道—北客站）小半径曲线段盾构隧道为工程背景，通过现场实测和数值模拟相结合的方法，探讨考虑千斤顶推力非对称分布及曲线内侧土体超挖情况下，小半径曲线段盾构隧道施工过程中地表变形规律及曲线半径对变形的影响，为建立更合理的曲线段盾构隧道开挖模型提供参考。

1 工程概况

西安地铁2 号线正北区间小半径曲线段（K0 +790.00 —K0 + 422.44）曲线半径为400 m，隧道平均埋深12 m，上覆杂填土，主要穿越中砂层。小半径曲线段平面和地质剖面见图1。

小半径曲线段采用土压平衡盾构机施工，盾构刀盘外径6.28 m，主机总长7.788 m，超挖刀最大伸出量85 mm。刀盘转速控制在1.0 ～ 1.4 r/min，掘进速度控制在25 ～ 40 mm/min，油压千斤顶推力为8 ～ 12 MN。管片采用钢筋混凝土管片，管片外径6.0 m，厚度0.3 m，宽度1.5 m，混凝土强度等级C50，抗渗等级为P12。衬砌采用错缝拼装方式，先拼装底部，按左右对称顺序逐块拼装，最后拼装封顶块。

2 现场监测

2.1 地表竖向位移监测方案

沿右线隧道轴线方向布设地表竖向位移测点，800 —832 环每隔7 环布设1 个，832—852 环每隔3 环布设1个，测点布置方案根据实际情况调整，以符合现场和研究的需要。编号方法为YZ + 编号，编号方向与隧道开挖方向一致。

以YZ3、YZ4、YZ5和YZ6测点为中心，沿隧道横向布置监测断面，编号方法为H + 编号。每个断面上布设7 个监测点，编号方向是从曲线内侧到曲线外侧。测点布设见图2。

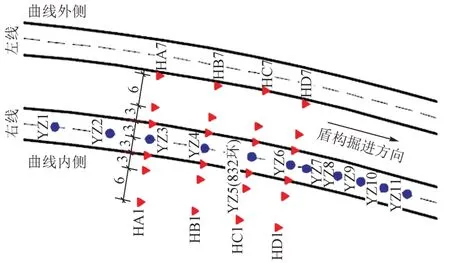
图2 监测点布设（单位：m）

2.2 监测数据分析

2.2.1 隧道纵向地表竖向位移

右线盾构机掘进至第832 环时，监测点YZ1—YZ11 地表竖向位移曲线见图3。可知：①盾构开挖面后方地表竖向位移呈现先增大后减小的趋势，位移最大值为16.1 mm，距开挖面19.5 m。②开挖面前方局部地表轻微隆起。最大隆起为1.77 mm，距开挖面25.5 m。

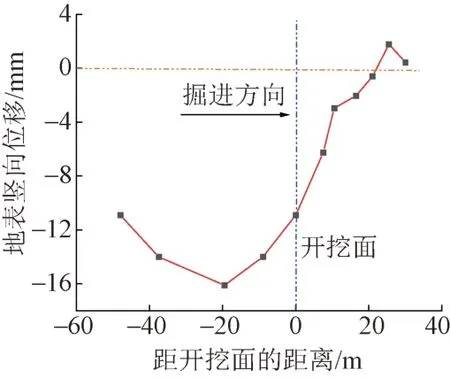
图3 隧道纵向地表竖向位移实测曲线

2.2.2 隧道横向地表竖向位移

右线盾构机掘进至第832 环时，监测断面HA、HB、HC、HD 处地表竖向位移曲线见图4。可知，沉降槽中线向曲线内侧偏移。距隧道轴线左右两侧3 m处，监测断面HA、HB、HC、HD 沉降差分别为8.53、3.00、11.23、3.50 mm。

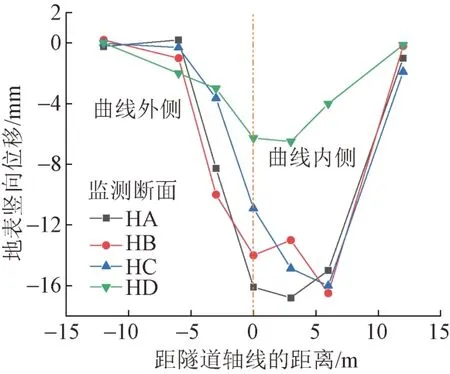
图4 不同监测断面地表竖向位移实测曲线

3 数值模拟

3.1 模型的建立

根据右线小半径曲线段地质条件及隧道设计参数建立计算模型，见图5。

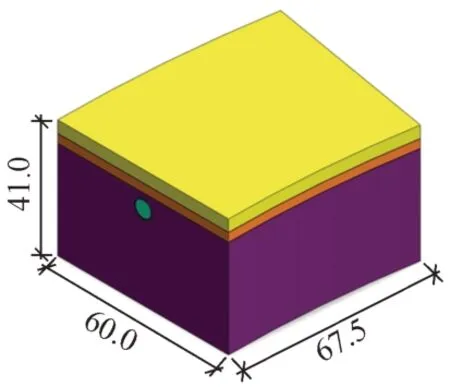
图5 计算模型（单位：m）

为了降低边界效应对计算结果的影响，同时提高计算效率，模型尺寸取长67.5 m（沿隧道轴线方向），宽60.0 m，高41.0 m。模型顶部采用自由边界，四周约束水平位移，底部约束竖向位移。土体采用摩尔库伦本构模型，注浆等代层和管片采用弹性体模型。土体物理力学参数根据现场地质勘察报告和工程经验取值，见表1。

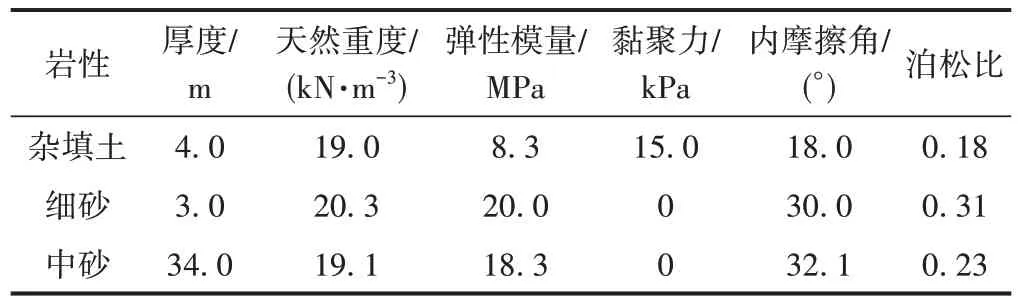
表1 土体物理力学参数

盾构在曲线段掘进时，为了实现盾构机的转弯，需增加曲线外侧的千斤顶推力。根据该区间工程地质资料，曲线外侧、内侧千斤顶推力分别设置为10、8 MN。模拟过程中将衬砌环划分为左右两个分区，并将千斤顶推力简化为作用在衬砌环上的均布荷载。

为了减小盾构机转向时的阻力，需对曲线内侧土体进行一定体积的超挖处理。土体超挖量理论计算公式［5］为

式中：δ为曲线段内侧土体超挖量；R0为曲线半径；D为盾构机直径；L为盾构机长度。

不考虑仿形刀伸缩的影响，通过在曲线内侧注浆等代层外设置半圆形超挖等代层来模拟曲线内侧土体超挖，见图6。根据本工程相关参数，经理论计算得到曲线半径为300、350、400、450 m 时超挖等代层厚度分别为25、21、19、17 mm。

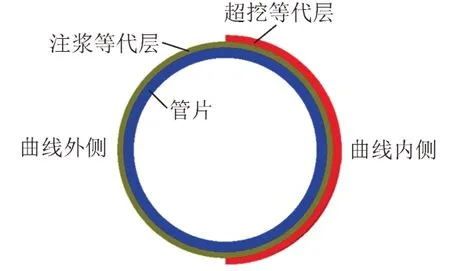
图6 曲线内侧土体超挖模拟

3.2 计算参数的确定

根据工程设计参数，盾构隧道管片内径2.7 m，幅宽1.5 m，厚度0.3 m，选用C50 钢筋混凝土材料。考虑到管片接头和错缝拼装的影响，将管片刚度按80%折减。注浆等代层、管片和盾壳的物理力学参数依据文献［12］并结合现场试验段测试结果取值，见表2。

表2 注浆等代层、管片和盾壳的物理力学参数

根据现场施工资料，注浆压力取0.25 MPa，土仓压力取0.15 MPa，注浆层厚度取0.018 m。

3.3 盾构掘进过程的模拟

采用刚度迁移法对盾构施工过程进行模拟。具体步骤：① 对模型施加初始应力；②通过null 命令将土体和超挖等代层单元改变为空单元模拟盾构开挖和曲线内侧土体的超挖；③在开挖面上施加均布荷载模拟土仓压力；④激活盾壳单元并给参数赋值模拟盾构机；⑤激活管片弹性体单元，模拟管片拼装；⑥将盾尾已拼装完成的管片分为左右两个分区，施加均布荷载模拟千斤顶分区推力；⑦盾尾脱出后，激活注浆层单元并施加径向荷载模拟盾尾同步注浆。

3.4 测点布置

仅模拟右线小半径曲线段盾构隧道812—832 环的掘进过程。将隧道轴线方向的纵剖面作为监测断面Ⅰ-Ⅰ'，沿着断面Ⅰ-Ⅰ'在地表每隔1.5 m布设1个位移监测点。第832 环横断面作为监测断面Ⅱ-Ⅱ'（对应实测的HC 监测断面），沿着断面Ⅱ-Ⅱ'在地表每隔0.5 m布设1个位移监测点。

3.5 模型验证

采用曲线半径400 m 的模型进行分析。掘进至第20 环时监测断面地表竖向位移模拟值与实测值对比见图7。

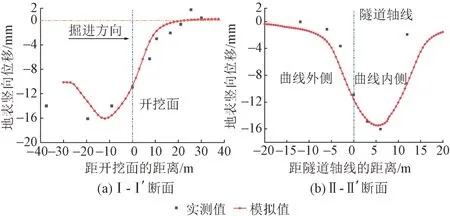
图7 各断面地表竖向位移模拟值与实测值对比

由图7可知：从总体上看，模拟值与实测值量级及变化规律一致，说明所建模型及参数选取比较合理。盾尾后方隧道纵向地表竖向位移实测值比模拟值大，可能是因为管片接头不严密，出现接头漏浆现象，从而降低管片支撑作用，使地表竖向位移增加。

3.6 计算结果分析

3.6.1 曲线半径对隧道纵向地表竖向位移的影响

盾构掘进至第20环时，不同曲线半径下隧道纵向地表竖向位移曲线见图8。可知：①由于盾构机刀盘对前方土体有挤压作用，开挖面前方一定范围内地表隆起。曲线半径为300、350、400、450 m 时开始隆起点距开挖面水平距离分别为21.0、22.5、22.5、22.5 m，平均距离约为22.1 m，隆起均小于1 mm。②开挖面前方地表竖向位移随距开挖面水平距离增加而逐渐减小。由于前方土体尚未开挖，前方地表竖向位移相对较小。曲线半径变化对开挖面前方地表竖向位移影响较小。③随距开挖面水平距离增加，开挖面后方地表沉降先增大后减小。由于盾尾处土体应力得到释放，加上盾尾间隙的影响，在盾构机后方地表沉降达到最大值。地表沉降最大值随曲线半径减小而逐渐增大。曲线半径为300、350、400、450 m 时地表沉降最大值分别为17.03、16.27、16.08、15.65 mm，距开挖面水平距离为12 m。12 m 以后，因盾壳脱离，土体应力释放产生回弹，土体抗变形能力提高，且随着管片的拼装，隧道整体刚度增大，地表沉降逐渐减小。曲线半径超过350 m 后，曲线半径变化对开挖面后方地表沉降影响较小。

3.6.2 曲线半径对隧道横向地表沉降的影响

盾构掘进至第20环时，不同曲线半径下隧道横向地表沉降曲线见图9。

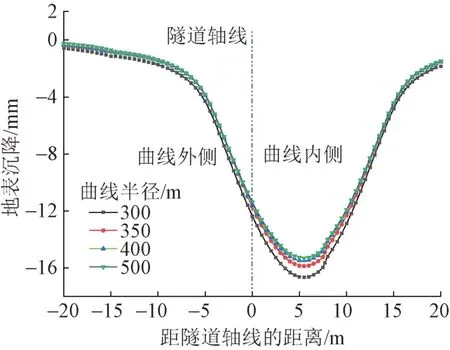
图9 不同曲线半径下隧道横向地表沉降曲线

由图9 可知：①盾构掘进过程中地表沉降槽形态呈V 形，与Peck 沉降槽相似。②沉降槽呈不对称分布，曲线内侧地表竖向位移大于曲线外侧，沉降槽中心线向曲线内侧偏离隧道轴线，偏移距离为5.5 m。原因是：为实现盾构曲线掘进，曲线外侧千斤顶推力需大于曲线内侧，使外侧土体受到挤压，产生一定程度的隆起，从而降低地表沉降。同时，受超挖影响，曲线内侧地层损失较大。③地表沉降最大值随曲线半径减小而增大。曲线半径超过350 m 后，半径变化对隧道横向地表沉降影响较小。

4 结论

依托实际工程案例，通过现场监测和数值模拟相结合的手段，分析小半径曲线段盾构隧道掘进过程中地表变形规律及曲线半径对地表竖向位移的影响。主要结论如下：

1）受刀盘挤压影响，盾构隧道开挖面前方约22.1 m 处地表会轻微隆起。受盾尾处土体应力释放及盾尾间隙影响，地表沉降最大值位于开挖面后方12 m 处。随着土体应力释放和管片的拼装，开挖面后方12 m以后地表沉降逐渐减小。

2）受千斤顶不对称推力和曲线内侧超挖影响，小半径曲线段盾构隧道横向地表沉降槽呈不对称分布，曲线内侧地表沉降大于曲线外侧，沉降槽中心线向曲线内侧偏离隧道轴线，偏移距离为5.5 m。

3）曲线半径对开挖面前方地表竖向位移影响较小，对开挖面后方地表沉降影响较大。随着曲线半径减小，隧道纵向、横向地表沉降最大值均逐渐增大。曲线半径超过350 m 后，半径变化对地表沉降影响较小。